27.1.2 圆的对称性 课件(35张PPT)
文档属性
| 名称 | 27.1.2 圆的对称性 课件(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-25 11:21:30 | ||
图片预览



文档简介
课件35张PPT。27.1 圆的认识圆的对称性 把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?可以发现:
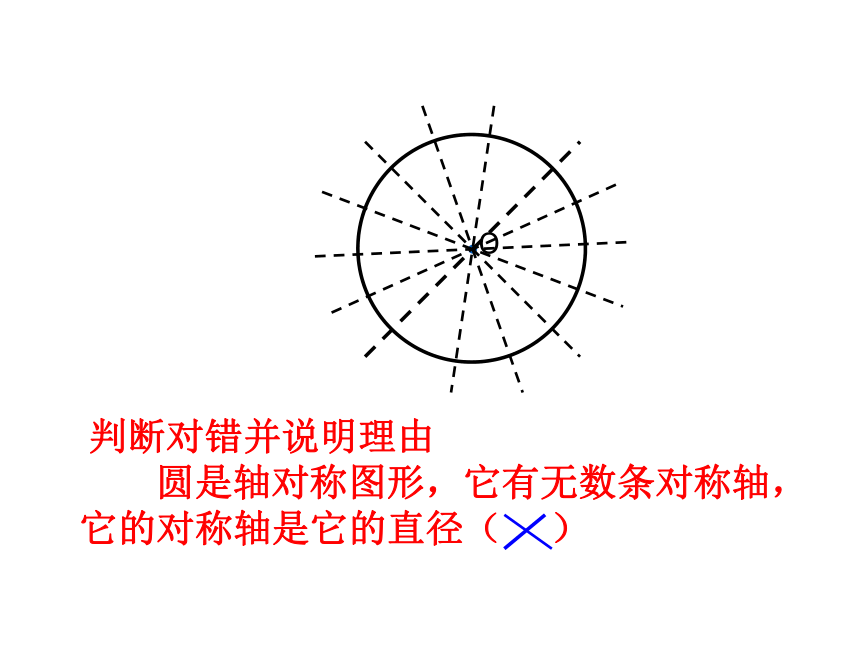
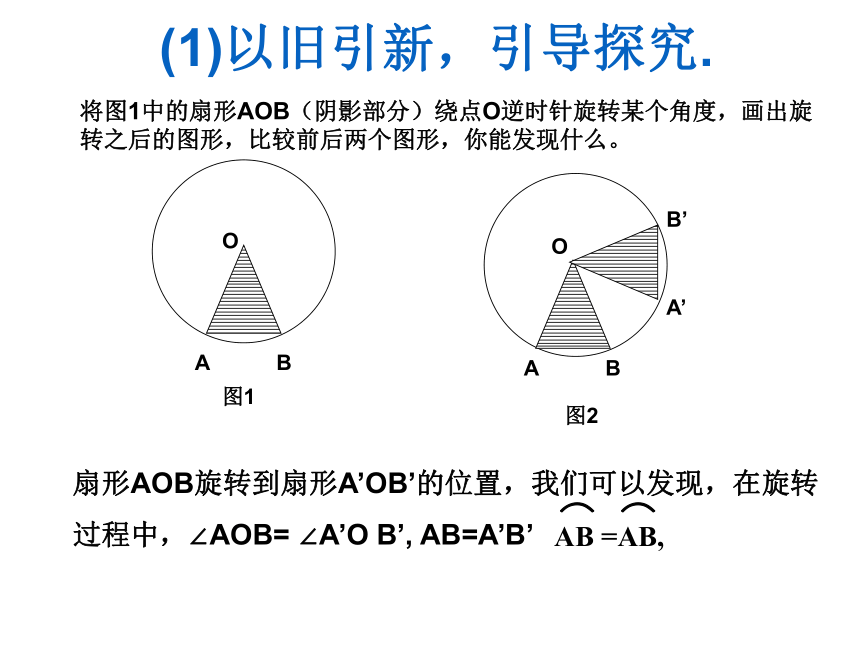
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 活动一 判断对错并说明理由 圆是轴对称图形,它有无数条对称轴,它的对称轴是它的直径( )将图1中的扇形AOB(阴影部分)绕点O逆时针旋转某个角度,画出旋转之后的图形,比较前后两个图形,你能发现什么。扇形AOB旋转到扇形A’OB’的位置,我们可以发现,在旋转
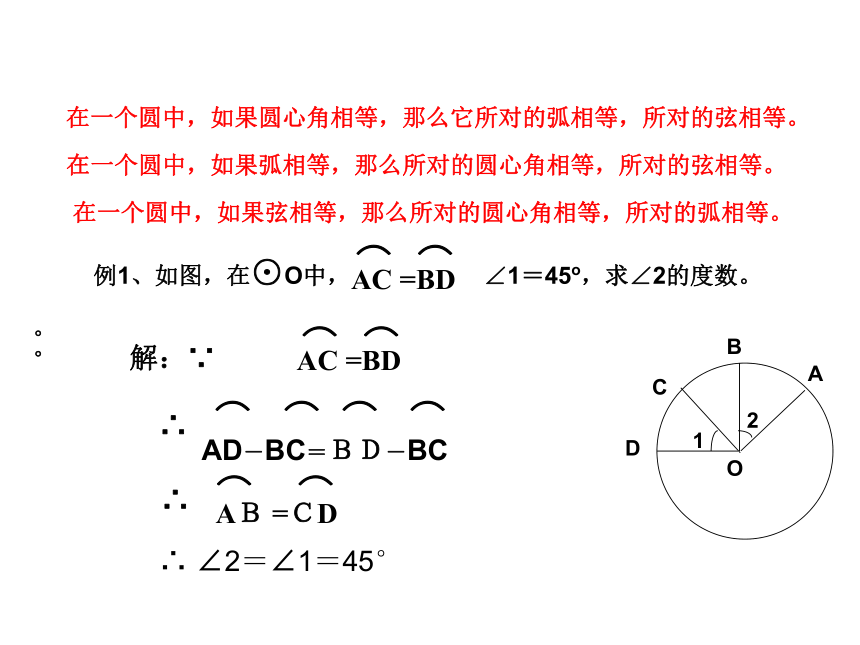
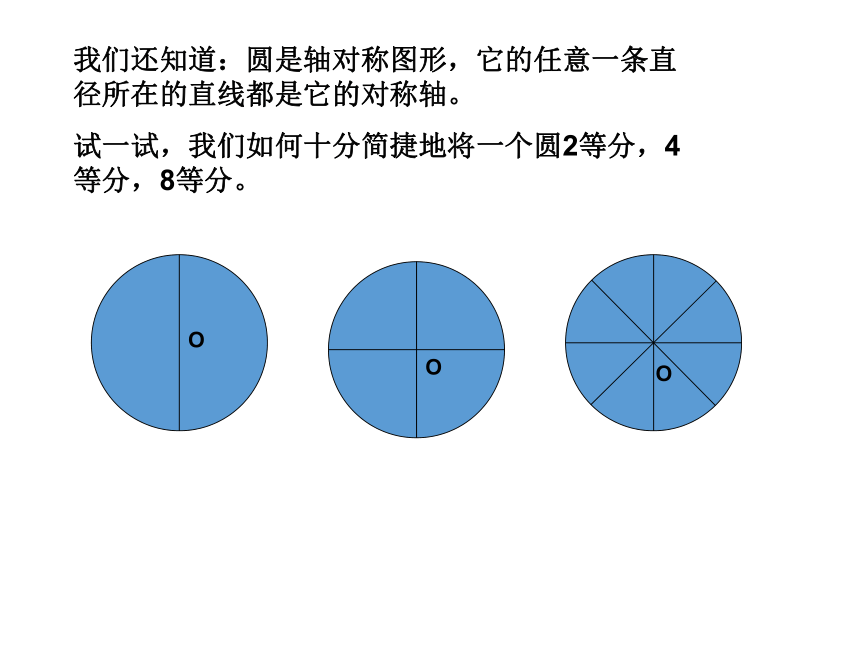
过程中,∠AOB= ∠A’O B’, AB=A’B’ (1)以旧引新,引导探究.在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等。在一个圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等。在一个圆中,如果弦相等,那么所对的圆心角相等,所对的弧相等。∴ ∠2=∠1=45°∴。我们还知道:圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴。
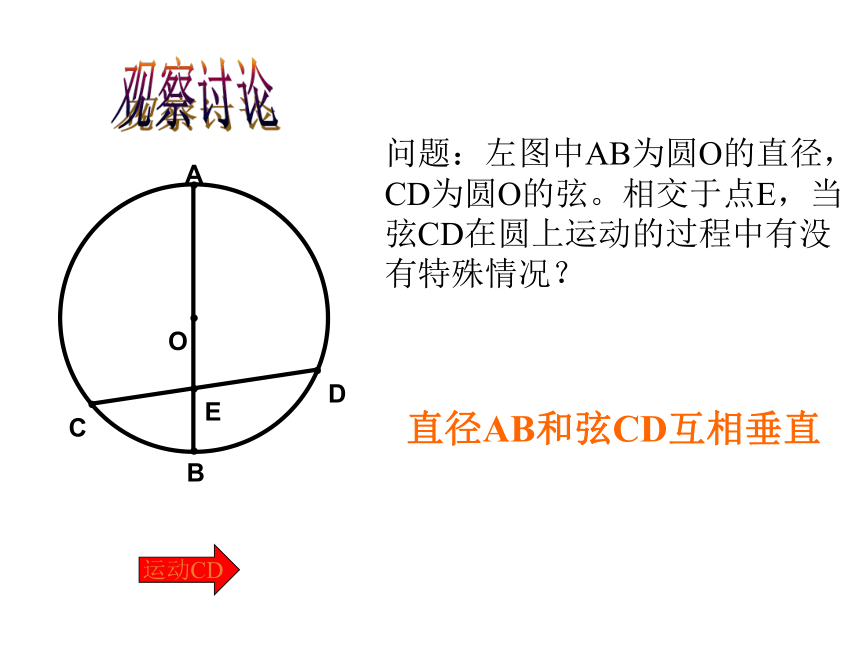
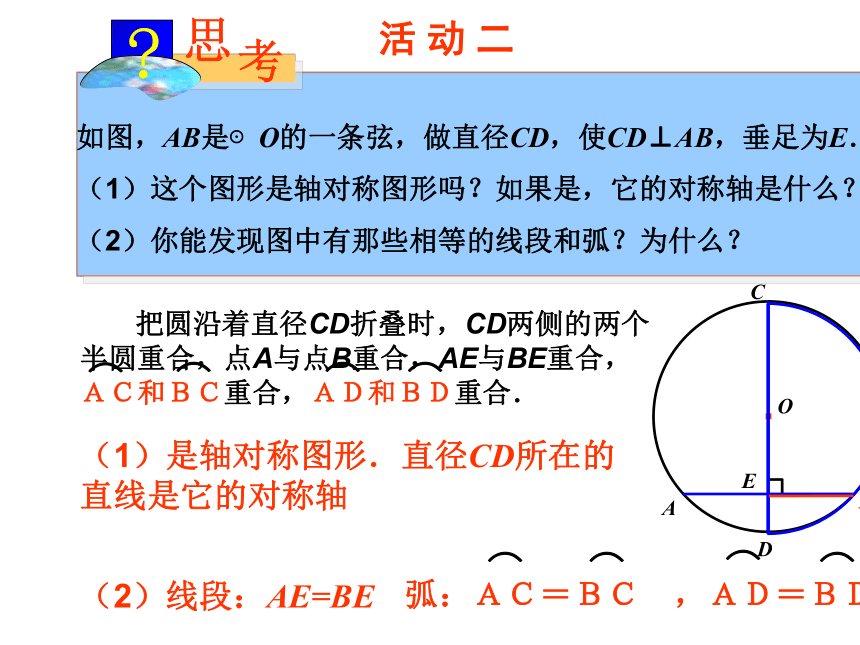
试一试,我们如何十分简捷地将一个圆2等分,4等分,8等分。问题:左图中AB为圆O的直径,CD为圆O的弦。相交于点E,当弦CD在圆上运动的过程中有没有特殊情况?运动CD直径AB和弦CD互相垂直观察讨论如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
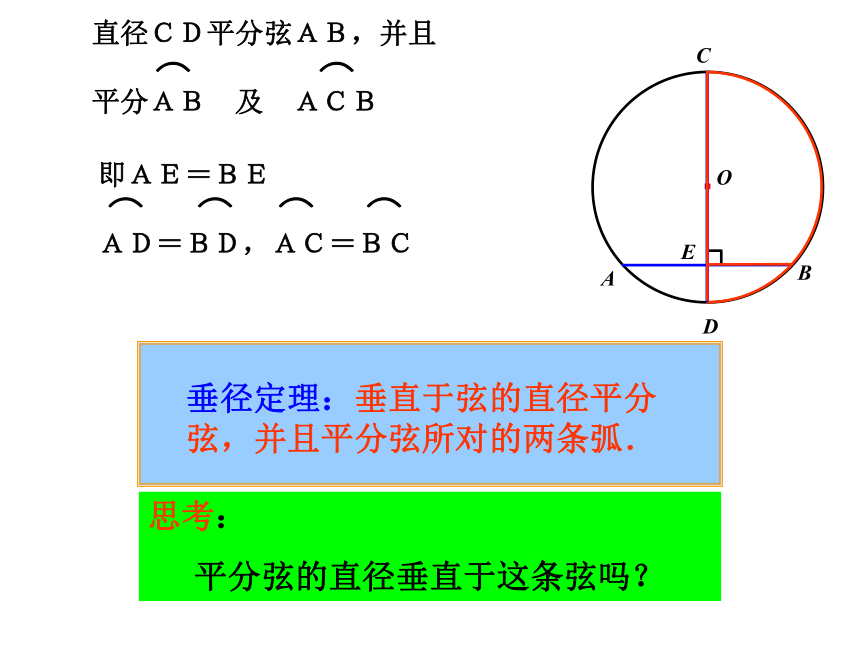
(2)你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二(1)是轴对称图形.直径CD所在的直线是它的对称轴(2)线段:AE=BE·OABCDE思考:
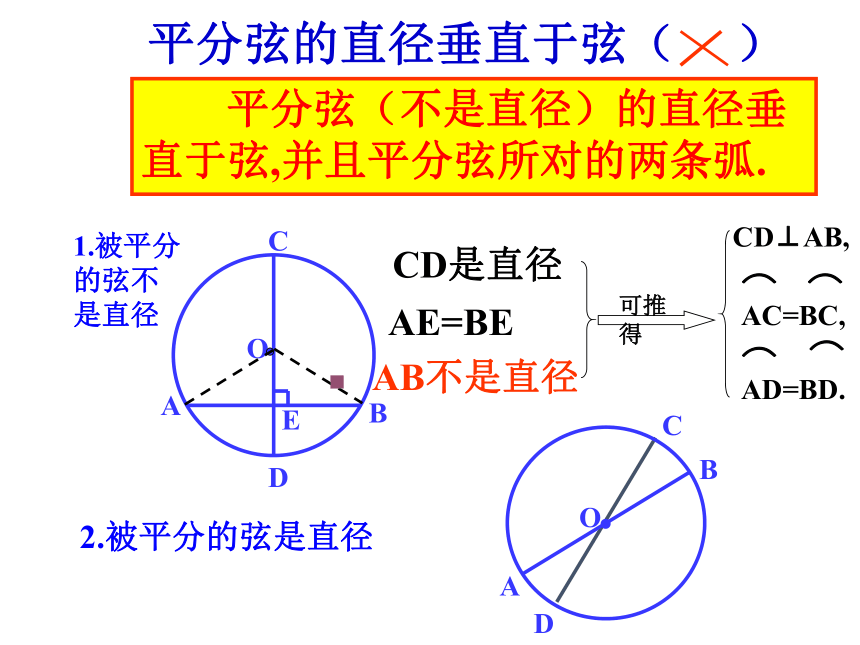
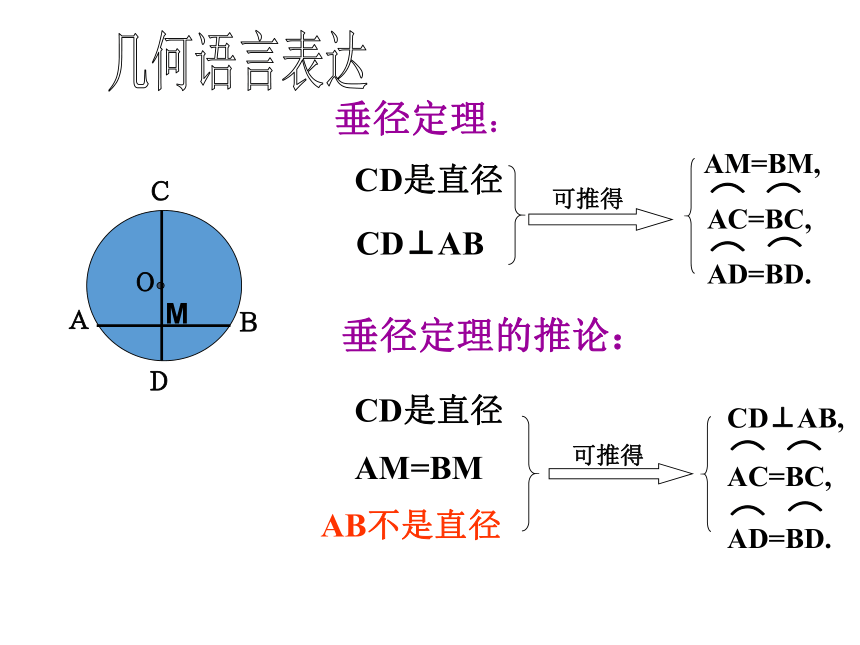
平分弦的直径垂直于这条弦吗? CD⊥AB, CD是直径 AE=BE 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.平分弦的直径垂直于弦( )CD1.被平分的弦不是直径2.被平分的弦是直径 AB不是直径AM=BM,CD是直径 CD⊥ABCD⊥AB,CD是直径AM=BMDCABMO几何语言表达垂径定理:垂径定理的推论: AB不是直径BADCOABDOABDOABCDO图1ABCDO图2OABCD图3图4图5图6EEEEE下列哪些图形可以用垂径定理,你能说明理由吗? 辨别是非总结: (3)指导论证,引申结论.五个条件 (1)垂直于弦
(2)过圆心
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧规律 知二推三垂径定理垂直于圆的直径平分圆,并且平分 圆所对的两条弧。总结1、文字语言2、符号语言3、图形语言条件结论(1)过圆心
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧分析CD为直径,
CD⊥AB}{垂径定理的几个基本图形 练习2、按图填空:在⊙O中,
(1)若MN⊥AB,MN为直径,
则________,________,________;
(2)若AC=BC,MN为直径,AB不是直径,
则________,________,________;
(3)若MN⊥AB,AC=BC,则________,________,________;
(4)若AN = BN ,MN为直径,则________,________,________.ABNMCO⌒⌒例1.判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线一定经过圆心⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 辨别是非例题解析 练1:如图,已知在圆O中,弦AB的长为8㎝,
圆心O到AB的距离为3 ㎝,求圆O的半径。练习:在半径为50㎜的圆O中,有长50㎜的
弦AB,计算:
⑴点O与AB的距离;
⑵∠AOB的度数。练2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。思路:(由)垂径定理——构造Rt△—— (结合)勾股定理——建立方程构造Rt△的“七字口诀”:
半径半弦弦心距 练习:
A组 在圆中某弦长为8cm,圆的直径是10cm,
则圆心到弦的距离是( )cm
B组 在圆o中弦CD=24,圆心到弦CD的距离
为5,则圆o的直径是( )
C组 若AB为圆O的直径,弦CD⊥AB于E,
AE=16,BE=4,则CD=( )
(4)多方练习,分层评价.答案:3答案:26答案:16例3 如图已知⊙O的直径为4cm,弦AB= cm,求∠OAB的度数。 (4)多方练习,分层评价.你还有没有其它方法?反思小结:
(5)反思小结,布置作业.1、对垂径定理的理解 (1)证明定理的方法是典型的“叠合法” (2)定理是解决有关弦的问题的重要方法 (3)定理中反映的弦的中点,弦所对的两条弧的中点都集中在“垂直于弦的直径”上。圆、弦又关于直径所在的直线对称。
2、关于垂径定理的运用 (1)辅助线的常用作法 (2)注意把问题化为解直角三角形的问题
例2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.1.已知:⊙O的半径为5 ,弦AB∥CD ,
AB = 6 ,CD =8 .
求: AB与CD间的距离 思考2.已知:如图,在同心圆O中,大⊙O的弦AB
交小⊙O于C,D两点
求证:AC=DBE实际应用某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?CNMAEHFBDO例:如图9,有一个拱桥是圆弧形,他的跨度为60m,拱高为18m,当洪水泛滥跨度小于30m时,要采取紧急措施.若拱顶离水面只有4m时,问是否要采取紧急措施? oMNE练3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
练习:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高为7.2m,求桥拱的半径(精确到0.1m).37.4米7.2米解决求赵州桥拱半径的问题如图,用 AB 表示主桥拱,设 AB所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是
AB 的中点,CD 就是拱高.⌒⌒⌒思考题已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF结束寄语不学自知,不问自晓,古今行事,未之有也.再见
圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 活动一 判断对错并说明理由 圆是轴对称图形,它有无数条对称轴,它的对称轴是它的直径( )将图1中的扇形AOB(阴影部分)绕点O逆时针旋转某个角度,画出旋转之后的图形,比较前后两个图形,你能发现什么。扇形AOB旋转到扇形A’OB’的位置,我们可以发现,在旋转
过程中,∠AOB= ∠A’O B’, AB=A’B’ (1)以旧引新,引导探究.在一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等。在一个圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等。在一个圆中,如果弦相等,那么所对的圆心角相等,所对的弧相等。∴ ∠2=∠1=45°∴。我们还知道:圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴。
试一试,我们如何十分简捷地将一个圆2等分,4等分,8等分。问题:左图中AB为圆O的直径,CD为圆O的弦。相交于点E,当弦CD在圆上运动的过程中有没有特殊情况?运动CD直径AB和弦CD互相垂直观察讨论如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二(1)是轴对称图形.直径CD所在的直线是它的对称轴(2)线段:AE=BE·OABCDE思考:
平分弦的直径垂直于这条弦吗? CD⊥AB, CD是直径 AE=BE 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.平分弦的直径垂直于弦( )CD1.被平分的弦不是直径2.被平分的弦是直径 AB不是直径AM=BM,CD是直径 CD⊥ABCD⊥AB,CD是直径AM=BMDCABMO几何语言表达垂径定理:垂径定理的推论: AB不是直径BADCOABDOABDOABCDO图1ABCDO图2OABCD图3图4图5图6EEEEE下列哪些图形可以用垂径定理,你能说明理由吗? 辨别是非总结: (3)指导论证,引申结论.五个条件 (1)垂直于弦
(2)过圆心
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧规律 知二推三垂径定理垂直于圆的直径平分圆,并且平分 圆所对的两条弧。总结1、文字语言2、符号语言3、图形语言条件结论(1)过圆心
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧分析CD为直径,
CD⊥AB}{垂径定理的几个基本图形 练习2、按图填空:在⊙O中,
(1)若MN⊥AB,MN为直径,
则________,________,________;
(2)若AC=BC,MN为直径,AB不是直径,
则________,________,________;
(3)若MN⊥AB,AC=BC,则________,________,________;
(4)若AN = BN ,MN为直径,则________,________,________.ABNMCO⌒⌒例1.判断下列说法的正误 ①平分弧的直径必平分弧所对的弦 ②平分弦的直线必垂直弦 ③垂直于弦的直径平分这条弦 ④平分弦的直径垂直于这条弦 ⑤弦的垂直平分线一定经过圆心⑥平分弦所对的一条弧的直径必垂直这条弦 ⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 辨别是非例题解析 练1:如图,已知在圆O中,弦AB的长为8㎝,
圆心O到AB的距离为3 ㎝,求圆O的半径。练习:在半径为50㎜的圆O中,有长50㎜的
弦AB,计算:
⑴点O与AB的距离;
⑵∠AOB的度数。练2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。思路:(由)垂径定理——构造Rt△—— (结合)勾股定理——建立方程构造Rt△的“七字口诀”:
半径半弦弦心距 练习:
A组 在圆中某弦长为8cm,圆的直径是10cm,
则圆心到弦的距离是( )cm
B组 在圆o中弦CD=24,圆心到弦CD的距离
为5,则圆o的直径是( )
C组 若AB为圆O的直径,弦CD⊥AB于E,
AE=16,BE=4,则CD=( )
(4)多方练习,分层评价.答案:3答案:26答案:16例3 如图已知⊙O的直径为4cm,弦AB= cm,求∠OAB的度数。 (4)多方练习,分层评价.你还有没有其它方法?反思小结:
(5)反思小结,布置作业.1、对垂径定理的理解 (1)证明定理的方法是典型的“叠合法” (2)定理是解决有关弦的问题的重要方法 (3)定理中反映的弦的中点,弦所对的两条弧的中点都集中在“垂直于弦的直径”上。圆、弦又关于直径所在的直线对称。
2、关于垂径定理的运用 (1)辅助线的常用作法 (2)注意把问题化为解直角三角形的问题
例2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.1.已知:⊙O的半径为5 ,弦AB∥CD ,
AB = 6 ,CD =8 .
求: AB与CD间的距离 思考2.已知:如图,在同心圆O中,大⊙O的弦AB
交小⊙O于C,D两点
求证:AC=DBE实际应用某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?CNMAEHFBDO例:如图9,有一个拱桥是圆弧形,他的跨度为60m,拱高为18m,当洪水泛滥跨度小于30m时,要采取紧急措施.若拱顶离水面只有4m时,问是否要采取紧急措施? oMNE练3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
练习:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高为7.2m,求桥拱的半径(精确到0.1m).37.4米7.2米解决求赵州桥拱半径的问题如图,用 AB 表示主桥拱,设 AB所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是
AB 的中点,CD 就是拱高.⌒⌒⌒思考题已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF结束寄语不学自知,不问自晓,古今行事,未之有也.再见
