27.1.3 圆周角 课件(共19张ppt)
文档属性
| 名称 | 27.1.3 圆周角 课件(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 329.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-25 11:21:30 | ||
图片预览




文档简介
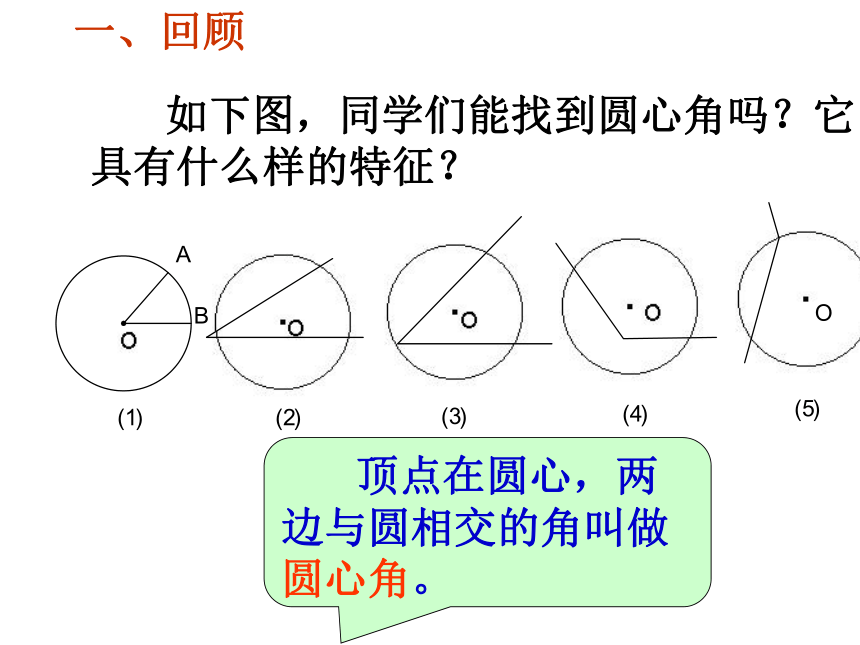
课件19张PPT。27.1圆的认识一、回顾 如下图,同学们能找到圆心角吗?它具有什么样的特征? 顶点在圆心,两边与圆相交的角叫做圆心角。 究竟什么样的角是圆周角呢? 像图(3)中的角就是圆周角,而图(1)、(2)、(4)、(5)中的角都不是圆周角。 二、认识圆周角
如何判断一个角是不是圆周角 ? 顶点在圆上,两边与圆相交的角叫做圆周角 。练习:指出下图中的圆周角。
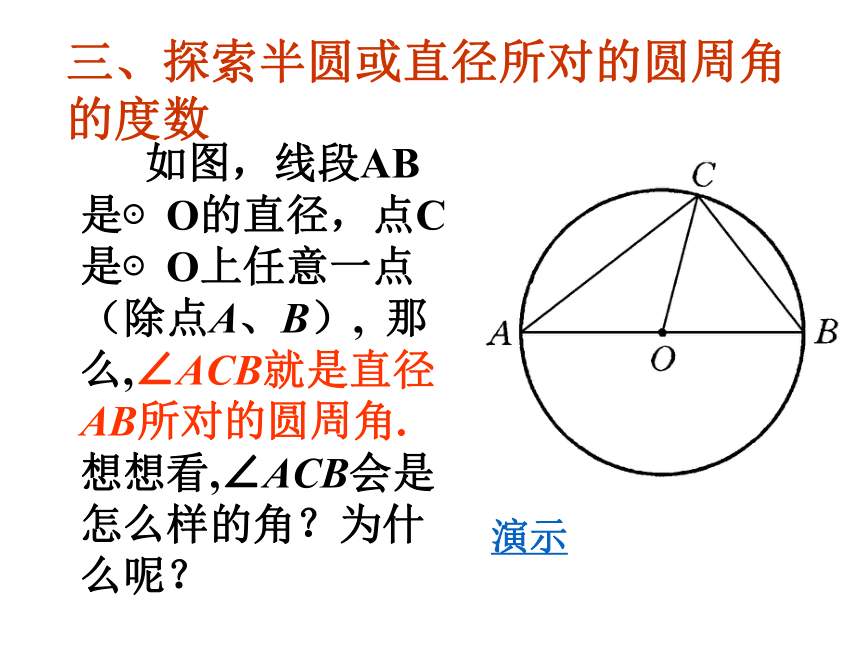
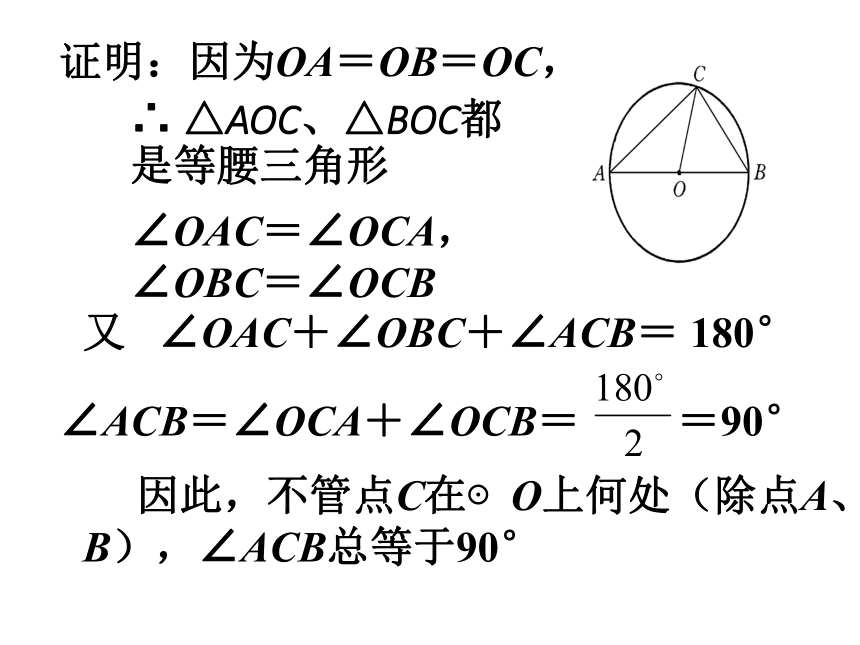
思考: ×√×××√ 如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢? 演示三、探索半圆或直径所对的圆周角的度数∴ △AOC、△BOC都是等腰三角形∠OAC=∠OCA,∠OBC=∠OCB又 ∠OAC+∠OBC+∠ACB= 180° ∠ACB=∠OCA+∠OCB= =90° 因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90° 证明:因为OA=OB=OC, 半圆或直径所对的圆周角都相等,都等于90°(直角)。 反过来也是成立的,即90°的圆周角所对的弦是圆的直径。结论 三、探究同一条弧所对的圆周角和圆心角的关系 1、分别量一量图中弧AB所对的两个圆周角的度数比较一下. 再变动点C在圆周上的位置,看看圆周角的
度数有没有变化. 你发
现其中有什么规律吗? ?
2、分别量出图23.1.10中弧AB所对的圆周角和圆心角的度数,比较一下,你发现什么?演示为了验证这个猜想,如图所示,可将圆对折,使折痕经过圆心O和圆周角的顶点C, 这时可能出现三种情况: (1) 折痕是圆周角的一条边,(2) 折痕在圆周角的内部, (3) 折痕在圆周角的外部。定理的证明
(1)圆心在∠BAC的一边上. 由于OA=OC因此∠C=∠BAC而∠BOC=∠BAC+∠C所以∠BAC= ∠BOC(2)圆心在∠BAC的内部.D作直径AD.由于∠BAD= ∠BOD12∠DAC= ∠DOC,12所以∠BAD+∠DAC=
(∠BOD+∠DOC)12即∠BAC= ∠BOC12(3)圆心在∠BAC的外部.D作直径AD.由于∠DAB= ∠DOB12∠DAC= ∠DOC,12所以∠DAC-∠DAB= (∠DOC-∠DOB)12即∠BAC= ∠BOC12结论: 在同一个圆或等圆中 ,同弧或等弧 所对的圆周角相等, 都等于该弧或等弧所对的 圆心角的一半; 相等的圆周角所对的弧也相等。 ∠ACB= ; ∠ADB= ;
∠ =∠ . 如图:则有ACBADB例 如图,AB为⊙O的直径, ∠A=80°,求∠ABC的度数。AO解:∵AB为⊙O的直径
∴∠C=90°,
又∠A=80°
∴ ∠B=10 °课后练习1、试找出图中
所有相等的圆周角。 3、在圆中,一条弧所对的圆心角和圆周角
分别为(2x+100)°和(5x-30)°,
求这条弧所对的圆心角和圆周角的度数.2、右图是一个圆形的零件,你能告诉我,它的圆心的位置吗?你有什么简捷的办法?
练习一:2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角x的度数。3、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________35°120°130°25°
(1)一个概念(圆周角)
内容小结:(2)一个定理:一条弧所对的圆周角等于
该弦所对的圆心角的一半;(3)二个推论: 半圆或直径所对的圆周角是直角;
90°的圆周角所对的弦是直径。 同圆内,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧相等。练习二:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形。证明:∵∠ABC和∠APC
都是 ⌒ 所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是 ⌒ 所对的圆周角,BC ∴∠BAC=∠CPB=60°。∴△ABC等边三角形。练习三已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,(同圆或等圆中,相等的圆周角所对弧相等)。
思考: ×√×××√ 如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢? 演示三、探索半圆或直径所对的圆周角的度数∴ △AOC、△BOC都是等腰三角形∠OAC=∠OCA,∠OBC=∠OCB又 ∠OAC+∠OBC+∠ACB= 180° ∠ACB=∠OCA+∠OCB= =90° 因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90° 证明:因为OA=OB=OC, 半圆或直径所对的圆周角都相等,都等于90°(直角)。 反过来也是成立的,即90°的圆周角所对的弦是圆的直径。结论 三、探究同一条弧所对的圆周角和圆心角的关系 1、分别量一量图中弧AB所对的两个圆周角的度数比较一下. 再变动点C在圆周上的位置,看看圆周角的
度数有没有变化. 你发
现其中有什么规律吗? ?
2、分别量出图23.1.10中弧AB所对的圆周角和圆心角的度数,比较一下,你发现什么?演示为了验证这个猜想,如图所示,可将圆对折,使折痕经过圆心O和圆周角的顶点C, 这时可能出现三种情况: (1) 折痕是圆周角的一条边,(2) 折痕在圆周角的内部, (3) 折痕在圆周角的外部。定理的证明
(1)圆心在∠BAC的一边上. 由于OA=OC因此∠C=∠BAC而∠BOC=∠BAC+∠C所以∠BAC= ∠BOC(2)圆心在∠BAC的内部.D作直径AD.由于∠BAD= ∠BOD12∠DAC= ∠DOC,12所以∠BAD+∠DAC=
(∠BOD+∠DOC)12即∠BAC= ∠BOC12(3)圆心在∠BAC的外部.D作直径AD.由于∠DAB= ∠DOB12∠DAC= ∠DOC,12所以∠DAC-∠DAB= (∠DOC-∠DOB)12即∠BAC= ∠BOC12结论: 在同一个圆或等圆中 ,同弧或等弧 所对的圆周角相等, 都等于该弧或等弧所对的 圆心角的一半; 相等的圆周角所对的弧也相等。 ∠ACB= ; ∠ADB= ;
∠ =∠ . 如图:则有ACBADB例 如图,AB为⊙O的直径, ∠A=80°,求∠ABC的度数。AO解:∵AB为⊙O的直径
∴∠C=90°,
又∠A=80°
∴ ∠B=10 °课后练习1、试找出图中
所有相等的圆周角。 3、在圆中,一条弧所对的圆心角和圆周角
分别为(2x+100)°和(5x-30)°,
求这条弧所对的圆心角和圆周角的度数.2、右图是一个圆形的零件,你能告诉我,它的圆心的位置吗?你有什么简捷的办法?
练习一:2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角x的度数。3、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________35°120°130°25°
(1)一个概念(圆周角)
内容小结:(2)一个定理:一条弧所对的圆周角等于
该弦所对的圆心角的一半;(3)二个推论: 半圆或直径所对的圆周角是直角;
90°的圆周角所对的弦是直径。 同圆内,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧相等。练习二:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形。证明:∵∠ABC和∠APC
都是 ⌒ 所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是 ⌒ 所对的圆周角,BC ∴∠BAC=∠CPB=60°。∴△ABC等边三角形。练习三已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,(同圆或等圆中,相等的圆周角所对弧相等)。
