27.1.3 圆周角 课件(共37张ppt)
文档属性
| 名称 | 27.1.3 圆周角 课件(共37张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-25 11:21:30 | ||
图片预览








文档简介
课件37张PPT。27.1 圆的认识第27章 圆3. 圆周角学习目标1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理解
决简单的几何问题.(重点、难点)
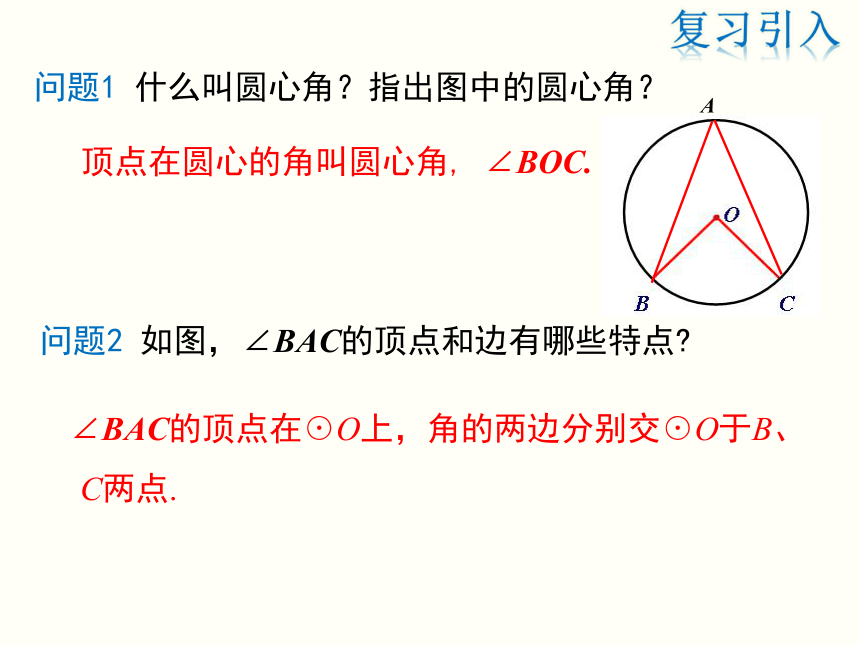
3.理解掌握圆周角定理的推论及其证明过程和运用.(难点) 问题1 什么叫圆心角?指出图中的圆心角? 顶点在圆心的角叫圆心角, ∠BOC.问题2 如图,∠BAC的顶点和边有哪些特点?A ∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.复习引入顶点在圆上,并且两边都与圆相交的角叫做圆周角.(两个条件必须同时具备,缺一不可)圆周角的定义新课讲解·COAB·COB·COBAA·COAB·COB·COBAA判一判:下列各图中的∠BAC是否为圆周角并简述理由.(2)(3)顶点不在圆上顶点不在圆上边AC没有和圆相交√√√新课讲解如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ABC 就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?解:∵OA=OB=OC,∴△AOC、
△BOC都是等腰三角形.∴ ∠OAC=∠OCA,∠OBC=∠OCB.又∵ ∠OAC+∠OBC+∠ACB=180°.∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.新课讲解圆周角和直径的关系圆周角和直径的关系:
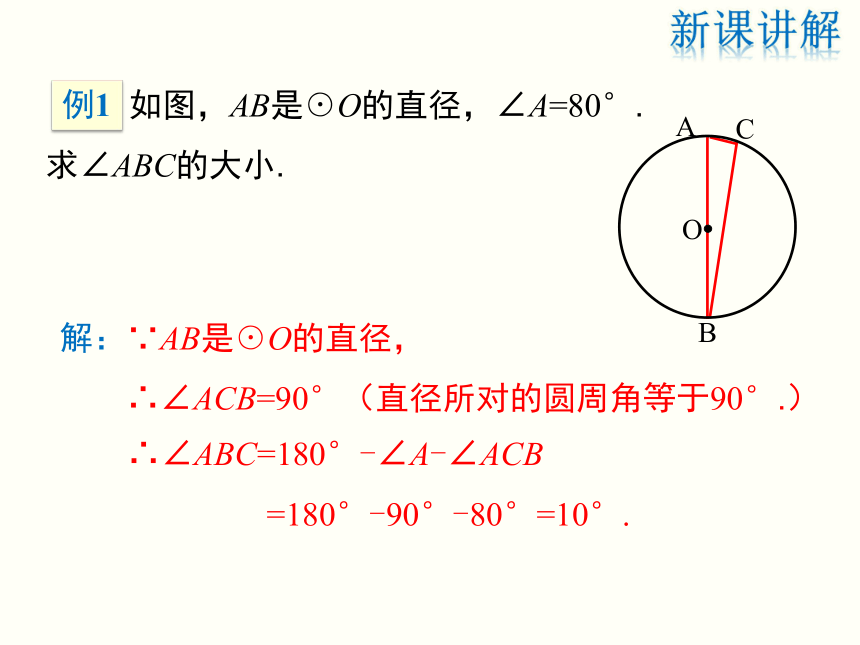
半圆或直径所对的圆周角都相等,都等于90°.新课讲解 如图,AB是☉O的直径,∠A=80°.求∠ABC的大小.解:∵AB是☉O的直径,
∴∠ACB=90°(直径所对的圆周角等于90°.)∴∠ABC=180°-∠A-∠ACB
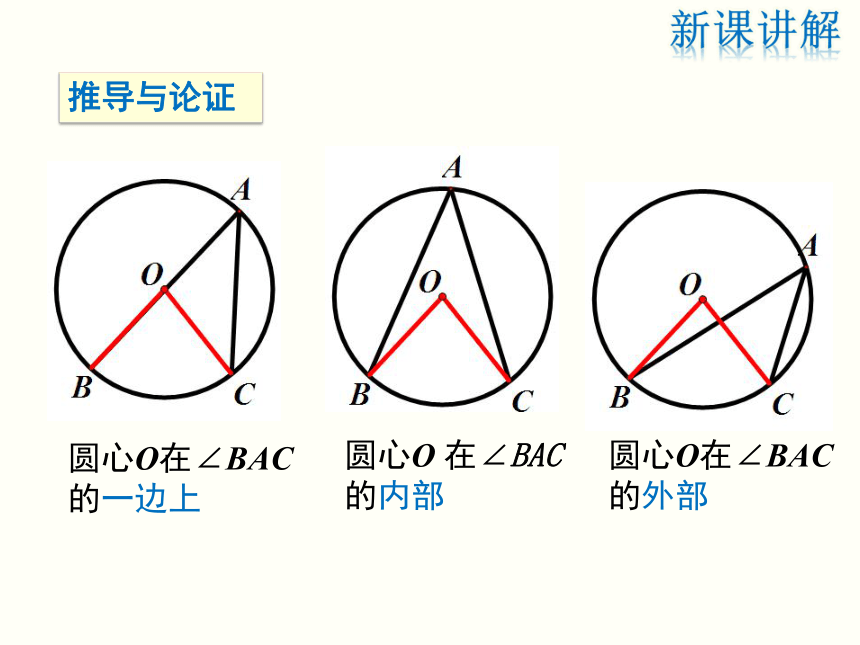
=180°-90°-80°=10°.新课讲解例1如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.圆周角定理及其推论新课讲解圆心O 在∠BAC 的内部圆心O在∠BAC的一边上圆心O在∠BAC
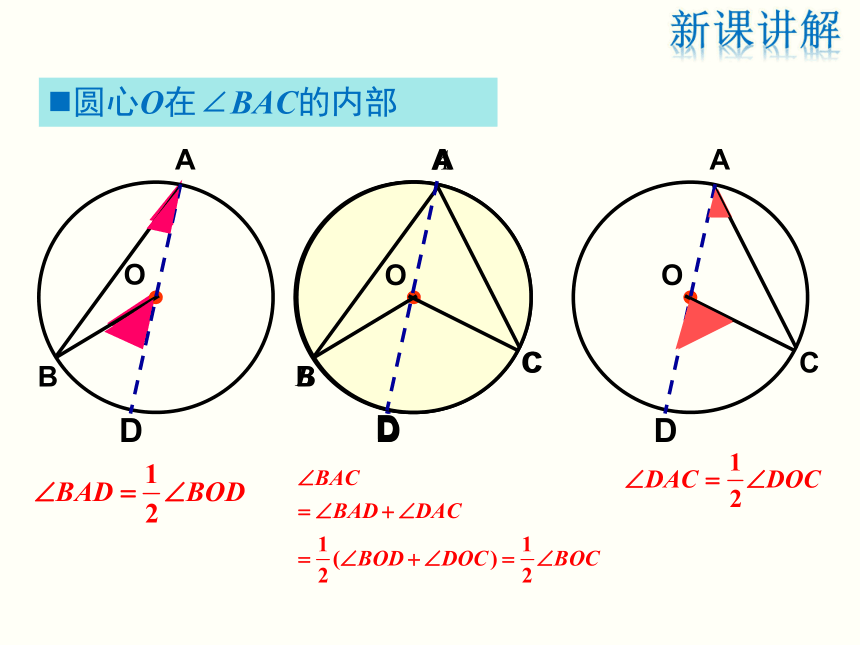
的外部新课讲解推导与论证圆心O在∠BAC的一边上(特殊情形)OA=OC∠A= ∠C∠BOC= ∠ A+ ∠C新课讲解圆心O在∠BAC的内部新课讲解圆心O在∠BAC的外部新课讲解问题1 如图,OB,OC都是⊙O的半径,点A ,D 是上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.∴∠BAC=∠BDC相等,理由如下:新课讲解相等(2)若CD是直径,你能求出∠A的度数吗?新课讲解圆周角定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;
相等的圆周角所对的弧也相等.圆周角定理 推论1:90°的圆周角所对的 弦是直径.新课讲解试一试:
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35o.(1)∠BOC= o,理由
是 ;
(2)∠BDC= o,理由是 .7035同弧所对的圆周角相等一条弧所对的圆周角等于它所对的圆心角的一半新课讲解(1)完成下列填空:
∠1= .
∠2= .
∠3= .
∠5= .2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.∠4∠8∠6∠7新课讲解 如图,分别求出图中∠x的大小.60°x30°20°x解:(1)∵同弧所对圆周角相等,∴∠x=60°.ADBEC(2)连接BF,F∵同弧所对圆周角相等,∴∠ABF=∠D=20°,∠FBC=∠E=30°.∴∠x=∠ABF+∠FBC=50°.新课讲解例2 如图,⊙O的直径AC为10cm,弦AD为6cm.
(1)求DC的长; (2)若∠ADC的平分线交⊙O
于B, 求AB、BC的长.B新课讲解例3在Rt△ABC中,AB2+BC2=AC2,(2)∵ AC是直径,
∴ ∠ABC=90°.
∵BD平分∠ADC,
∴∠ADB=∠CDB.
又∵∠ACB=∠ADB , ∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC. 提示:解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.新课讲解如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°解析:∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.故选C.方法总结:在圆中,如果有直径,一般要找直径所对的圆周角,构造直角三角形解题.随堂即练 如图,AB是⊙O的直径,弦CD交AB于点P,
∠ACD=60°,∠ADC=70°.求∠APC的度数.解:连结BC,则∠ACB=90°,∠DCB=∠ACB-∠ACD=
90°-60°=30°.又∵∠BAD=∠DCB=30°,∴∠APC=∠BAD+∠ADC=30°+70°=100°.新课讲解例4 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.方法总结:圆内接四边形的性质是沟通角相等关系的重要依据.新课讲解例5如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是 ( )
A.120° B.100°
C.80° D.60°解析:∵∠BOD=120°,∴∠A=60°,∴∠C=180°-60°=120°,故选A.A随堂即练解:设∠A,∠B,∠C的度数分别对于2x,3x,6x, 在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰6.求这个四边形各角的度数.∵四边形ABCD内接于圆,∴ ∠A + ∠C=∠B+∠D=180°.∵2x+6x=180°,∴ x=22.5°,∴ ∠A=45°, ∠B=67.5°, ∠C =135°,
∠D=180°- 67.5°=112.5°.新课讲解例61.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )√××随堂即练2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,
∠ABC=47°, 则∠AOB= .
166°随堂即练3.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为 ( )
A.30° B.40° C.50° D.60°A【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.随堂即练4.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是
( )
A. 115° B.130°
C.65° D. 50°
5.如图,等边三角形ABC内接于⊙O,P是AB上的一点,则∠APB= .C120°随堂即练6.如图,已知圆心角∠AOB=100°,则圆周角
∠ACB= ,∠ADB= .130°50°随堂即练7.如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是 .解析:连结OA、OB,∵∠C=30° ,∴∠AOB=60°.又∵OA=OB ,
∴△AOB是等边三角形.∴OA=OB=AB=2,即半径为2.2随堂即练∴∠ACB=2∠BAC证明:8. 如图,OA,OB,OC都是⊙O的半径,∠AOB=
2∠BOC. 求证:∠ACB=2∠BAC.∠AOB=2∠BOC,随堂即练能力提升∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC, ∴BD=CD.∵AD平分顶角∠BAC,即∠BAD=∠CAD,(同圆或等圆中相等的圆周角所对弧相等)解:BD=CD.理由是:连结AD,能力提升圆心角类比圆周角圆周角定义圆周角定理在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
线的关系半圆或直径所对的圆周角都相等,都等于90°(直角).
课堂小结
2.理解圆周角与圆心角的关系并能运用圆周角定理解
决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论及其证明过程和运用.(难点) 问题1 什么叫圆心角?指出图中的圆心角? 顶点在圆心的角叫圆心角, ∠BOC.问题2 如图,∠BAC的顶点和边有哪些特点?A ∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.复习引入顶点在圆上,并且两边都与圆相交的角叫做圆周角.(两个条件必须同时具备,缺一不可)圆周角的定义新课讲解·COAB·COB·COBAA·COAB·COB·COBAA判一判:下列各图中的∠BAC是否为圆周角并简述理由.(2)(3)顶点不在圆上顶点不在圆上边AC没有和圆相交√√√新课讲解如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ABC 就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?解:∵OA=OB=OC,∴△AOC、
△BOC都是等腰三角形.∴ ∠OAC=∠OCA,∠OBC=∠OCB.又∵ ∠OAC+∠OBC+∠ACB=180°.∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.新课讲解圆周角和直径的关系圆周角和直径的关系:
半圆或直径所对的圆周角都相等,都等于90°.新课讲解 如图,AB是☉O的直径,∠A=80°.求∠ABC的大小.解:∵AB是☉O的直径,
∴∠ACB=90°(直径所对的圆周角等于90°.)∴∠ABC=180°-∠A-∠ACB
=180°-90°-80°=10°.新课讲解例1如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.圆周角定理及其推论新课讲解圆心O 在∠BAC 的内部圆心O在∠BAC的一边上圆心O在∠BAC
的外部新课讲解推导与论证圆心O在∠BAC的一边上(特殊情形)OA=OC∠A= ∠C∠BOC= ∠ A+ ∠C新课讲解圆心O在∠BAC的内部新课讲解圆心O在∠BAC的外部新课讲解问题1 如图,OB,OC都是⊙O的半径,点A ,D 是上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.∴∠BAC=∠BDC相等,理由如下:新课讲解相等(2)若CD是直径,你能求出∠A的度数吗?新课讲解圆周角定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;
相等的圆周角所对的弧也相等.圆周角定理 推论1:90°的圆周角所对的 弦是直径.新课讲解试一试:
1.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35o.(1)∠BOC= o,理由
是 ;
(2)∠BDC= o,理由是 .7035同弧所对的圆周角相等一条弧所对的圆周角等于它所对的圆心角的一半新课讲解(1)完成下列填空:
∠1= .
∠2= .
∠3= .
∠5= .2.如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.∠4∠8∠6∠7新课讲解 如图,分别求出图中∠x的大小.60°x30°20°x解:(1)∵同弧所对圆周角相等,∴∠x=60°.ADBEC(2)连接BF,F∵同弧所对圆周角相等,∴∠ABF=∠D=20°,∠FBC=∠E=30°.∴∠x=∠ABF+∠FBC=50°.新课讲解例2 如图,⊙O的直径AC为10cm,弦AD为6cm.
(1)求DC的长; (2)若∠ADC的平分线交⊙O
于B, 求AB、BC的长.B新课讲解例3在Rt△ABC中,AB2+BC2=AC2,(2)∵ AC是直径,
∴ ∠ABC=90°.
∵BD平分∠ADC,
∴∠ADB=∠CDB.
又∵∠ACB=∠ADB , ∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC. 提示:解答圆周角有关问题时,若题中出现“直径”这个条件,则考虑构造直角三角形来求解.新课讲解如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°解析:∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.故选C.方法总结:在圆中,如果有直径,一般要找直径所对的圆周角,构造直角三角形解题.随堂即练 如图,AB是⊙O的直径,弦CD交AB于点P,
∠ACD=60°,∠ADC=70°.求∠APC的度数.解:连结BC,则∠ACB=90°,∠DCB=∠ACB-∠ACD=
90°-60°=30°.又∵∠BAD=∠DCB=30°,∴∠APC=∠BAD+∠ADC=30°+70°=100°.新课讲解例4 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.方法总结:圆内接四边形的性质是沟通角相等关系的重要依据.新课讲解例5如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是 ( )
A.120° B.100°
C.80° D.60°解析:∵∠BOD=120°,∴∠A=60°,∴∠C=180°-60°=120°,故选A.A随堂即练解:设∠A,∠B,∠C的度数分别对于2x,3x,6x, 在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰6.求这个四边形各角的度数.∵四边形ABCD内接于圆,∴ ∠A + ∠C=∠B+∠D=180°.∵2x+6x=180°,∴ x=22.5°,∴ ∠A=45°, ∠B=67.5°, ∠C =135°,
∠D=180°- 67.5°=112.5°.新课讲解例61.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )√××随堂即练2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,
∠ABC=47°, 则∠AOB= .
166°随堂即练3.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为 ( )
A.30° B.40° C.50° D.60°A【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.随堂即练4.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是
( )
A. 115° B.130°
C.65° D. 50°
5.如图,等边三角形ABC内接于⊙O,P是AB上的一点,则∠APB= .C120°随堂即练6.如图,已知圆心角∠AOB=100°,则圆周角
∠ACB= ,∠ADB= .130°50°随堂即练7.如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是 .解析:连结OA、OB,∵∠C=30° ,∴∠AOB=60°.又∵OA=OB ,
∴△AOB是等边三角形.∴OA=OB=AB=2,即半径为2.2随堂即练∴∠ACB=2∠BAC证明:8. 如图,OA,OB,OC都是⊙O的半径,∠AOB=
2∠BOC. 求证:∠ACB=2∠BAC.∠AOB=2∠BOC,随堂即练能力提升∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC, ∴BD=CD.∵AD平分顶角∠BAC,即∠BAD=∠CAD,(同圆或等圆中相等的圆周角所对弧相等)解:BD=CD.理由是:连结AD,能力提升圆心角类比圆周角圆周角定义圆周角定理在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
线的关系半圆或直径所对的圆周角都相等,都等于90°(直角).
课堂小结
