27.2.3 切线——切线的判定 课件(23张PPT)
文档属性
| 名称 | 27.2.3 切线——切线的判定 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 358.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-25 00:00:00 | ||
图片预览






文档简介
课件23张PPT。 切 线 的 判 定【学习目标】1.知识与技能
掌握切线的判定定理,会证明一条直线是圆的切线.
2、过程与方法
1).在探究圆的切线的判定与性质定理的过程中,培养学生的动手操作能力和演绎归纳能力,渗透分类讨论的基本思想.
2).在运用圆的切线的判定与性质定理进行证明的过程中感受几何推理的严谨性,培养学生的逻辑推理能力.3、情感、态度与价值观
1).通在证明问题中,感受数学推理的严谨性,培养学生良好的学习习惯.
2).在自主探究中体会成功的快乐,增强学好数学的信心,在分组交流中培养协作意识. 【学习重难点】重点和难点是理解并掌握切线的
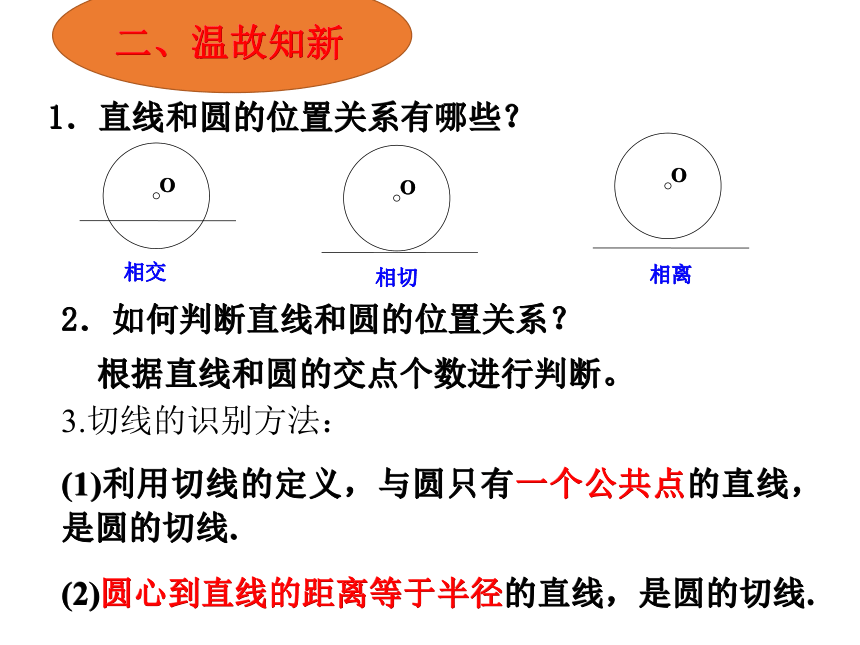
判定定理及其应用【学法指导】 本节课在学习过程中注重动手操作、观察、发现、总结等活动去发现相关结论,在解决问题中培养分析问题和解决问题的能力,总结常用辅助线的做法.1.下雨天,当你转动雨伞,你会发现雨伞上的水珠顺着伞面的边缘飞出.仔细观察一下,水珠是顺着什么样的方向飞出的? 2.用机床打磨铁制零件时,铁屑是沿什么方向飞出的? 3.行驶中的火车,火车的车轮与笔直的铁轨给我们什么形象? 一、情境引入 二、温故知新 1.直线和圆的位置关系有哪些?2.如何判断直线和圆的位置关系?3.切线的识别方法:(1)利用切线的定义,与圆只有一个公共点的直线, 是圆的切线.
(2)圆心到直线的距离等于半径的直线,是圆的切线.
根据直线和圆的交点个数进行判断。相切相离相交根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢?
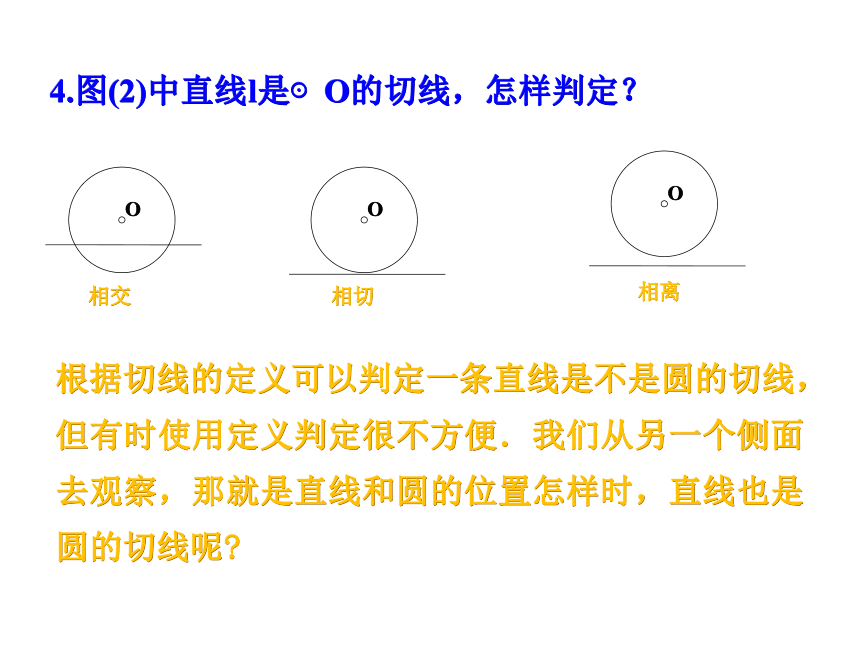
4.图(2)中直线l是⊙O的切线,怎样判定? 三、 设问导读阅读课本P51-52的内容完成下列问题:1.自己任意画一个圆并作出一条半径,过半径的外端作一条与半径垂直的直线,观察直线与圆有几个交点,分析这条直线与圆有何位置关系2.在1中的作图中具备了什么条件?总结:切线的判定定理 .
3.自学例2:例2中有哪些已知条件?有哪些特殊图形?要证明结论,只需证明 . 经过半径的外端且垂直
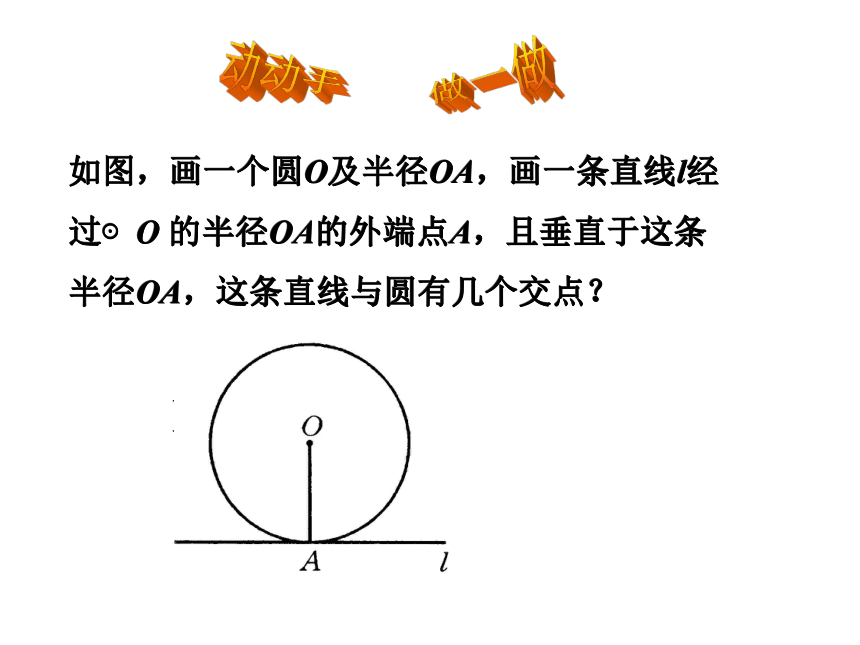
于这条半径的直线是圆的切线.如图,画一个圆O及半径OA,画一条直线l经过⊙O 的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?动动手做一做 从图中可以看出,此时直线与圆只有_________,即直线l是圆的切线.
经过半径的外端且垂直于
这条半径的直线是圆的切线.一个交点直线与圆相切的判定定理:对定理的理解: 切线需满足两条:
①经过半径外端;
②垂直于这条半径. 切线的识别方法(1)利用切线的定义,与圆只有 的直线, 是圆的切线;(2) 的直线,是圆的切线;(3)经过半径的外端且垂直于一个公共点圆心到直线的距离等于半径 这条半径的
直线是圆的切线.1. 是非题:
⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过半径的端点并且垂直于这条直径的直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切线。
)(×)(×)四、自学检测(×)(√)利用判定定理时,要注意直线须具备以下两个条件,缺一不可
(1)直线经过半径的外端;
(2)直线与这半径垂直。 2、如图,AB为⊙O的直径,BC为⊙O的切线, AC交⊙O于点D.图中互余的角有( ) A 1对 B 2对
C 3对 D 4对
D小结:当直线与圆有公共点,常连接 和公共点得半径,证明直线垂直于 . 3、 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明 AB⊥OC即可。 证明:连结OC(如图)。
∵ ⊿OAB中, OA=OB , CA=CB,
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。圆心半径4、已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。(分析: AC 与圆没有公共点,应该选用哪种判定方法?怎样作辅助线?)OE=OD方法小结:当直线与圆没有公共点,常过圆心作直线
的 ,证明圆心到直线的距离等于 .半径垂线.1.下列说法正确的是 ( )
A.与圆有公共点的直线是圆的切线.
B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线;
D.过圆的半径的外端的直线是圆的切线
五、巩固练习 B2. 如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D. BD是⊙O的切线吗?为什么?. 由∠BAD=30°,
得出∠BOD=60 °.因为在△ODB中,由∠B=30°,
∠BOD=60 °, 得∠BDO=90°,所以, BD是⊙O的切线.是解: 因为由∠B=45°,AC=AB,根据等腰三角形的性质,得出∠BAC=90 °,而OA是⊙O的半径,根据“经过半径的外端且垂直于这条半径的直线是圆的切线”,因此, AC是⊙O的切线. 3. 如图,AB是⊙O的直径,∠B=45°,AC=AB.
AC是⊙O的切线吗?为什么? 解:是. 1.切线的识别方法(三种): (1)利用切线的定义,与圆只有一个公共点的直线, 是圆的切线; (2)圆心到直线的距离等于半径的直线,是圆的切线;(3)经过半径的外端且垂直于这条半径的直线是圆的切线. 六、小结2.常用的添辅助线方法? ⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径) 证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OPB=∠C。 ∴OP∥AC。
∵PE⊥AC,∴∠PEC= 90°
∴∠OPE= ∠PEC= 90°
∴PE为⊙0的切线。1.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E。
求证:PE是⊙O的切线。OABCEP七、拓展延伸2.已知:如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论. 直线DE与⊙O相切.理由如下:过点O作AF交圆O于F点,连接BF.
∵∠F,∠C是同弧AB所对的角,∴∠C=∠AFB,∵∠BAE=∠C,∴∠BAE=∠F,∵AF为直径,∴∠ABF=90°,
∴在三角形ABF中∠AFB+∠BAF=90°,∵∠AFB=∠BAE,∴∠BAE+∠BAF=90°,∴FA⊥DE,∴直线DE与⊙O相切.
掌握切线的判定定理,会证明一条直线是圆的切线.
2、过程与方法
1).在探究圆的切线的判定与性质定理的过程中,培养学生的动手操作能力和演绎归纳能力,渗透分类讨论的基本思想.
2).在运用圆的切线的判定与性质定理进行证明的过程中感受几何推理的严谨性,培养学生的逻辑推理能力.3、情感、态度与价值观
1).通在证明问题中,感受数学推理的严谨性,培养学生良好的学习习惯.
2).在自主探究中体会成功的快乐,增强学好数学的信心,在分组交流中培养协作意识. 【学习重难点】重点和难点是理解并掌握切线的
判定定理及其应用【学法指导】 本节课在学习过程中注重动手操作、观察、发现、总结等活动去发现相关结论,在解决问题中培养分析问题和解决问题的能力,总结常用辅助线的做法.1.下雨天,当你转动雨伞,你会发现雨伞上的水珠顺着伞面的边缘飞出.仔细观察一下,水珠是顺着什么样的方向飞出的? 2.用机床打磨铁制零件时,铁屑是沿什么方向飞出的? 3.行驶中的火车,火车的车轮与笔直的铁轨给我们什么形象? 一、情境引入 二、温故知新 1.直线和圆的位置关系有哪些?2.如何判断直线和圆的位置关系?3.切线的识别方法:(1)利用切线的定义,与圆只有一个公共点的直线, 是圆的切线.
(2)圆心到直线的距离等于半径的直线,是圆的切线.
根据直线和圆的交点个数进行判断。相切相离相交根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢?
4.图(2)中直线l是⊙O的切线,怎样判定? 三、 设问导读阅读课本P51-52的内容完成下列问题:1.自己任意画一个圆并作出一条半径,过半径的外端作一条与半径垂直的直线,观察直线与圆有几个交点,分析这条直线与圆有何位置关系2.在1中的作图中具备了什么条件?总结:切线的判定定理 .
3.自学例2:例2中有哪些已知条件?有哪些特殊图形?要证明结论,只需证明 . 经过半径的外端且垂直
于这条半径的直线是圆的切线.如图,画一个圆O及半径OA,画一条直线l经过⊙O 的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?动动手做一做 从图中可以看出,此时直线与圆只有_________,即直线l是圆的切线.
经过半径的外端且垂直于
这条半径的直线是圆的切线.一个交点直线与圆相切的判定定理:对定理的理解: 切线需满足两条:
①经过半径外端;
②垂直于这条半径. 切线的识别方法(1)利用切线的定义,与圆只有 的直线, 是圆的切线;(2) 的直线,是圆的切线;(3)经过半径的外端且垂直于一个公共点圆心到直线的距离等于半径 这条半径的
直线是圆的切线.1. 是非题:
⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过半径的端点并且垂直于这条直径的直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切线。
)(×)(×)四、自学检测(×)(√)利用判定定理时,要注意直线须具备以下两个条件,缺一不可
(1)直线经过半径的外端;
(2)直线与这半径垂直。 2、如图,AB为⊙O的直径,BC为⊙O的切线, AC交⊙O于点D.图中互余的角有( ) A 1对 B 2对
C 3对 D 4对
D小结:当直线与圆有公共点,常连接 和公共点得半径,证明直线垂直于 . 3、 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明 AB⊥OC即可。 证明:连结OC(如图)。
∵ ⊿OAB中, OA=OB , CA=CB,
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。圆心半径4、已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。(分析: AC 与圆没有公共点,应该选用哪种判定方法?怎样作辅助线?)OE=OD方法小结:当直线与圆没有公共点,常过圆心作直线
的 ,证明圆心到直线的距离等于 .半径垂线.1.下列说法正确的是 ( )
A.与圆有公共点的直线是圆的切线.
B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线;
D.过圆的半径的外端的直线是圆的切线
五、巩固练习 B2. 如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D. BD是⊙O的切线吗?为什么?. 由∠BAD=30°,
得出∠BOD=60 °.因为在△ODB中,由∠B=30°,
∠BOD=60 °, 得∠BDO=90°,所以, BD是⊙O的切线.是解: 因为由∠B=45°,AC=AB,根据等腰三角形的性质,得出∠BAC=90 °,而OA是⊙O的半径,根据“经过半径的外端且垂直于这条半径的直线是圆的切线”,因此, AC是⊙O的切线. 3. 如图,AB是⊙O的直径,∠B=45°,AC=AB.
AC是⊙O的切线吗?为什么? 解:是. 1.切线的识别方法(三种): (1)利用切线的定义,与圆只有一个公共点的直线, 是圆的切线; (2)圆心到直线的距离等于半径的直线,是圆的切线;(3)经过半径的外端且垂直于这条半径的直线是圆的切线. 六、小结2.常用的添辅助线方法? ⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径) 证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OPB=∠C。 ∴OP∥AC。
∵PE⊥AC,∴∠PEC= 90°
∴∠OPE= ∠PEC= 90°
∴PE为⊙0的切线。1.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E。
求证:PE是⊙O的切线。OABCEP七、拓展延伸2.已知:如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论. 直线DE与⊙O相切.理由如下:过点O作AF交圆O于F点,连接BF.
∵∠F,∠C是同弧AB所对的角,∴∠C=∠AFB,∵∠BAE=∠C,∴∠BAE=∠F,∵AF为直径,∴∠ABF=90°,
∴在三角形ABF中∠AFB+∠BAF=90°,∵∠AFB=∠BAE,∴∠BAE+∠BAF=90°,∴FA⊥DE,∴直线DE与⊙O相切.
