27.2.3 切线 课件(28张PPT)
文档属性
| 名称 | 27.2.3 切线 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-25 11:21:30 | ||
图片预览








文档简介
课件28张PPT。第27章 圆27.2 与圆有关的位置关系第3课时 切 线 1课堂讲解切线的判定
切线的性质2课时流程逐点
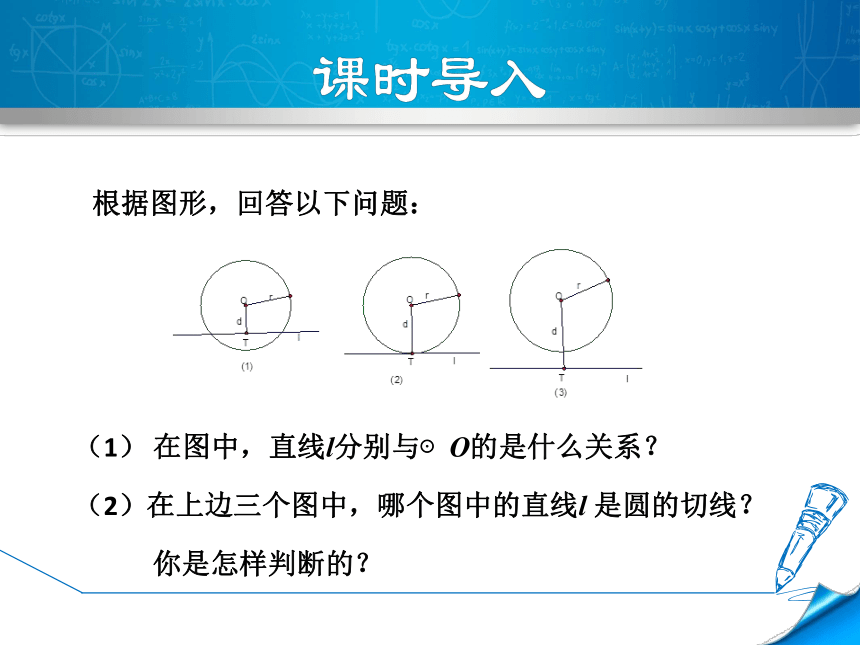
导讲练课堂小结作业提升根据图形,回答以下问题:(1) 在图中,直线l分别与⊙O的是什么关系?
(2)在上边三个图中,哪个图中的直线l 是圆的切线?
你是怎样判断的?1知识点切线的判定知1-导如图,画一个圆O及半径OA,经过⊙ O的半径OA的外端
点A画一条直线l垂直于这条半 径,这条直线与圆有几个
公共点?(来自《教材》)知1-导从图可以看出,对直线l上除点A外的任一 点P,
必有OP > OA,即点P立于圆外,从而可知直线与 圆只
有一个公共点,所以直线l是圆的切线.知1-讲1. 判定定理:经过圆的半径的外端且垂直于这条半径的直
线是圆的切线.
要点精析:切线必须同时具备两个条件:
(1)直线过半径的外端;(2)直线垂直于半径.
2. 判定方法:
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量法:圆心到直线的距离等于半径的直线是圆的切线;
(3)判定定理:经过半径的外端并且垂直于这条半径的直线是
圆的切线.知1-讲3. 切线判定常用的证明方法:
(1)有切点,连半径,证垂直:
如果已知直线经过圆上的一点,那么连结这点和圆心,得到
辅助半径,再证明所作半径与这条直线垂直即可,简记为:
有切点,连半径,证垂直.
(2)无切点,作垂直,证半径:
如果已知条件中不知道直线与圆是否有公共点,那么过圆心
作直线的垂线段,再证明垂线段的长度等于半径即可,简记
为:无切点,作垂直,证半径.如图,已知AB为⊙O的直径,点D在AB的延长线上,
BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.知1-讲例1因为点C在圆上,所以连结
OC,证明OC⊥CD,而要
证OC⊥CD,只需证△OCD为直角三角形.导引:知1-讲如图,连结OC,BC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC= A B=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°.
又OC是⊙O的半径,∴DC是⊙O的切线.证明:知1-讲(1)解答本题运用了连半径,证垂直.一定要分清圆
的切线的判定定理的条件与结论,特别要注意“经过
半径(或直径)的外端”和“垂直于这条半径(或直径)”这
两个条件缺一不可,否则就不是圆的切线.(2)如果
要证的切线过圆上某一点,那么连结这点和圆心(连
半径),证明该直线与过这点的半径垂直(证垂直),即
可判定直线与圆相切,这就是:连半径,证垂直.如图,在Rt△ABC中,∠B=90°,
∠BAC的平分线交BC于点D,以点
D为圆心,DB为半径作⊙D.
求证:AC与⊙D相切.知1-讲例2直线AC是否与⊙D有公共点不确定,不能像上例那样
“连半径,证垂直”,为此,过D点作DF⊥AC于点F,
由d=r?直线与圆相切可知,只需证DF=DB即可.导引:知1-讲如图,过点D作DF⊥AC于点F.
∵∠B=90°,
∴DB⊥AB.
又∵AD平分∠BAC,
∴DF=DB.
∴AC与⊙D相切.证明:知1-讲如果已知条件中不知道直线与圆是否有公共点,其证
法是过圆心作直线的垂线段,再证明垂线段的长等于
半径即可,简记为:作垂直,证半径.如图,AB是⊙O的直径, ∠B = ∠ CAD, 求证:AC
是⊙O的切线.知1-练(来自《教材》)下列命题中,真命题是( )
A.垂直于半径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到某直线的距离等于半径,那么这条直线
是圆的切线知1-练如图,△ABC是⊙O的内接三角形,下列选项中,能
使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C
B.∠B=90°
C.EF⊥AC
D.AC是⊙O的直径知1-练2知识点切线的性质知2-导如图,如果直线l是⊙O的切线,点A为切点,那么半径
OA与l垂直吗?知2-讲1. 性质定理:圆的切线垂直于经过切点的半径.
要点精析:
(1)性质定理的题设有两个条件:
①圆的切线;②半径过切点,应用时缺一不可.
(2)切线的判定定理与性质定理的区别:切线的判定定理
是在未知相切而要证明相切的情况下使用,切线的性
质定理是在已知相切而要推得其他的结论时使用;它
们是一个互逆的过程,不要混淆.知2-讲2. 切线的性质:
温故:(1)切线和圆只有一个公共点;
(2)圆心到切线的距离等于半径;
(3)圆的切线垂直于过切点的半径.
知新:(推论)
(4)经过圆心且垂直于切线的直线必过切点(找切点用);
(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
以上(3)(4)(5)可归纳为:知2-讲已知直线满足:①过圆心;②过切点;③垂直于切线
中的任意两个,就可得到第三个.
拓展:
(1)弦切角的定义:顶点在圆上,一边与圆相交(弦),另
一边与圆相切(切线)的角叫做弦切角.
(2)弦切角的性质:弦切角的度数等于它所夹弧所对的
圆周角的度数,亦等于它所夹弧的度数的一半,也
等于它所夹弧所对的圆心角度数的一半. 如图,在△ABC中,AB=1,AC= , 点O在AB
的延长线上,AC切⊙O于点C.
(1)求⊙O的半径;
(2)求∠A的度数.知2-讲例3(1)连结OC,易得Rt△OAC,运用勾股定理求⊙O的半
径;(2)在Rt△OAC中,利用锐角三角函数求∠A的度
数.导引:知2-讲(1)如图,连结OC.∵AC切⊙O于点C,
∴OC⊥AC,设⊙O的半径为r,
则OC=OB=r.
∴OA=OB+AB=1+r.
在Rt△OAC中,OA2=OC2+AC2,
即(1+r)2=r2+( )2,解得r=1.故⊙O的半径为1.
(2)由(1)得OC=1,OA=2.
在Rt△OAC中,sin A= ,∴∠A=30°.解:知2-讲当圆中有切线和切点时,通常连结过切点的半径,则
这条半径必与切线垂直.本例中作辅助线的方法,适
用于同类条件下与圆有关的求值或证明题.(2015·吉林)如图,在⊙O中,AB为直径,BC为
弦,CD为切线,连结OC.若∠BCD=50°,则∠AOC的度数为( )
A.40°
B.50°
C.80°
D.100°知2-练知2-练(2015·泸州)如图,PA,PB分别与⊙O相切于A,B
两点,若∠C=65°,则∠P的度数为( )
A.65°
B.130°
C.50°
D.100°知2-练(2015·内江)如图,在⊙O的内接四边形ABCD中,AB
是直径,∠BCD=120°,过D点的切线PD与直线AB
交于点P,则∠ADP的度数为( )
A.40°
B.35°
C.30°
D.45°1.证明直线与圆相切有如下三种途径:
(1)定义法:和圆有且只有一个公共点的直线是圆的
切线.
(2)数量法(d=r):圆心到直线的距离等于半径的
直线是圆的切线.
(3)判定定理:经过半径的外端并且垂直于这条半径
的直线是圆的切线.2.作辅助线的两种方法:
(1)若直线与圆的公共点未指明,则过圆心作直线的垂线段,
然后说明这条垂线段的长等于圆的半径;即“作垂直,
证半径”.
(2)若直线与圆的一个公共点已指明,则连结这点和圆心,
说明直线垂直于经过这点的半径;即“连半径,证垂直”.
3.切线的性质定理:圆的切线垂直于过且点的半径。
4.已知直线满足:①过圆心;②过切点;③垂直于切线中的
任意两个,就可得到第三个.
切线的性质2课时流程逐点
导讲练课堂小结作业提升根据图形,回答以下问题:(1) 在图中,直线l分别与⊙O的是什么关系?
(2)在上边三个图中,哪个图中的直线l 是圆的切线?
你是怎样判断的?1知识点切线的判定知1-导如图,画一个圆O及半径OA,经过⊙ O的半径OA的外端
点A画一条直线l垂直于这条半 径,这条直线与圆有几个
公共点?(来自《教材》)知1-导从图可以看出,对直线l上除点A外的任一 点P,
必有OP > OA,即点P立于圆外,从而可知直线与 圆只
有一个公共点,所以直线l是圆的切线.知1-讲1. 判定定理:经过圆的半径的外端且垂直于这条半径的直
线是圆的切线.
要点精析:切线必须同时具备两个条件:
(1)直线过半径的外端;(2)直线垂直于半径.
2. 判定方法:
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量法:圆心到直线的距离等于半径的直线是圆的切线;
(3)判定定理:经过半径的外端并且垂直于这条半径的直线是
圆的切线.知1-讲3. 切线判定常用的证明方法:
(1)有切点,连半径,证垂直:
如果已知直线经过圆上的一点,那么连结这点和圆心,得到
辅助半径,再证明所作半径与这条直线垂直即可,简记为:
有切点,连半径,证垂直.
(2)无切点,作垂直,证半径:
如果已知条件中不知道直线与圆是否有公共点,那么过圆心
作直线的垂线段,再证明垂线段的长度等于半径即可,简记
为:无切点,作垂直,证半径.如图,已知AB为⊙O的直径,点D在AB的延长线上,
BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.知1-讲例1因为点C在圆上,所以连结
OC,证明OC⊥CD,而要
证OC⊥CD,只需证△OCD为直角三角形.导引:知1-讲如图,连结OC,BC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC= A B=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°.
又OC是⊙O的半径,∴DC是⊙O的切线.证明:知1-讲(1)解答本题运用了连半径,证垂直.一定要分清圆
的切线的判定定理的条件与结论,特别要注意“经过
半径(或直径)的外端”和“垂直于这条半径(或直径)”这
两个条件缺一不可,否则就不是圆的切线.(2)如果
要证的切线过圆上某一点,那么连结这点和圆心(连
半径),证明该直线与过这点的半径垂直(证垂直),即
可判定直线与圆相切,这就是:连半径,证垂直.如图,在Rt△ABC中,∠B=90°,
∠BAC的平分线交BC于点D,以点
D为圆心,DB为半径作⊙D.
求证:AC与⊙D相切.知1-讲例2直线AC是否与⊙D有公共点不确定,不能像上例那样
“连半径,证垂直”,为此,过D点作DF⊥AC于点F,
由d=r?直线与圆相切可知,只需证DF=DB即可.导引:知1-讲如图,过点D作DF⊥AC于点F.
∵∠B=90°,
∴DB⊥AB.
又∵AD平分∠BAC,
∴DF=DB.
∴AC与⊙D相切.证明:知1-讲如果已知条件中不知道直线与圆是否有公共点,其证
法是过圆心作直线的垂线段,再证明垂线段的长等于
半径即可,简记为:作垂直,证半径.如图,AB是⊙O的直径, ∠B = ∠ CAD, 求证:AC
是⊙O的切线.知1-练(来自《教材》)下列命题中,真命题是( )
A.垂直于半径的直线是圆的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到某直线的距离等于半径,那么这条直线
是圆的切线知1-练如图,△ABC是⊙O的内接三角形,下列选项中,能
使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C
B.∠B=90°
C.EF⊥AC
D.AC是⊙O的直径知1-练2知识点切线的性质知2-导如图,如果直线l是⊙O的切线,点A为切点,那么半径
OA与l垂直吗?知2-讲1. 性质定理:圆的切线垂直于经过切点的半径.
要点精析:
(1)性质定理的题设有两个条件:
①圆的切线;②半径过切点,应用时缺一不可.
(2)切线的判定定理与性质定理的区别:切线的判定定理
是在未知相切而要证明相切的情况下使用,切线的性
质定理是在已知相切而要推得其他的结论时使用;它
们是一个互逆的过程,不要混淆.知2-讲2. 切线的性质:
温故:(1)切线和圆只有一个公共点;
(2)圆心到切线的距离等于半径;
(3)圆的切线垂直于过切点的半径.
知新:(推论)
(4)经过圆心且垂直于切线的直线必过切点(找切点用);
(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
以上(3)(4)(5)可归纳为:知2-讲已知直线满足:①过圆心;②过切点;③垂直于切线
中的任意两个,就可得到第三个.
拓展:
(1)弦切角的定义:顶点在圆上,一边与圆相交(弦),另
一边与圆相切(切线)的角叫做弦切角.
(2)弦切角的性质:弦切角的度数等于它所夹弧所对的
圆周角的度数,亦等于它所夹弧的度数的一半,也
等于它所夹弧所对的圆心角度数的一半. 如图,在△ABC中,AB=1,AC= , 点O在AB
的延长线上,AC切⊙O于点C.
(1)求⊙O的半径;
(2)求∠A的度数.知2-讲例3(1)连结OC,易得Rt△OAC,运用勾股定理求⊙O的半
径;(2)在Rt△OAC中,利用锐角三角函数求∠A的度
数.导引:知2-讲(1)如图,连结OC.∵AC切⊙O于点C,
∴OC⊥AC,设⊙O的半径为r,
则OC=OB=r.
∴OA=OB+AB=1+r.
在Rt△OAC中,OA2=OC2+AC2,
即(1+r)2=r2+( )2,解得r=1.故⊙O的半径为1.
(2)由(1)得OC=1,OA=2.
在Rt△OAC中,sin A= ,∴∠A=30°.解:知2-讲当圆中有切线和切点时,通常连结过切点的半径,则
这条半径必与切线垂直.本例中作辅助线的方法,适
用于同类条件下与圆有关的求值或证明题.(2015·吉林)如图,在⊙O中,AB为直径,BC为
弦,CD为切线,连结OC.若∠BCD=50°,则∠AOC的度数为( )
A.40°
B.50°
C.80°
D.100°知2-练知2-练(2015·泸州)如图,PA,PB分别与⊙O相切于A,B
两点,若∠C=65°,则∠P的度数为( )
A.65°
B.130°
C.50°
D.100°知2-练(2015·内江)如图,在⊙O的内接四边形ABCD中,AB
是直径,∠BCD=120°,过D点的切线PD与直线AB
交于点P,则∠ADP的度数为( )
A.40°
B.35°
C.30°
D.45°1.证明直线与圆相切有如下三种途径:
(1)定义法:和圆有且只有一个公共点的直线是圆的
切线.
(2)数量法(d=r):圆心到直线的距离等于半径的
直线是圆的切线.
(3)判定定理:经过半径的外端并且垂直于这条半径
的直线是圆的切线.2.作辅助线的两种方法:
(1)若直线与圆的公共点未指明,则过圆心作直线的垂线段,
然后说明这条垂线段的长等于圆的半径;即“作垂直,
证半径”.
(2)若直线与圆的一个公共点已指明,则连结这点和圆心,
说明直线垂直于经过这点的半径;即“连半径,证垂直”.
3.切线的性质定理:圆的切线垂直于过且点的半径。
4.已知直线满足:①过圆心;②过切点;③垂直于切线中的
任意两个,就可得到第三个.
