第4节 简单机械(杠杆) 学案(无答案)
文档属性
| 名称 | 第4节 简单机械(杠杆) 学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2019-06-26 08:37:59 | ||
图片预览

文档简介
1.杠杆的定义
1.杠杆基本知识
简图
定义 在力的作用下绕着________转动的硬棒叫杠杆
五要素 支点 杠杆绕着转动的点,一般用字母O表示
动力 使杠杆转动的力,一般用字母F1 表示
阻力 阻碍杠杆转动的力,一般用字母F2 表示
动力臂 从支点到动力作用线的距离,一般用字母l1表示
阻力臂 从支点到阻力作用线的距离,一般用字母l2表示
说明 动力、阻力都是杠杆受的力,所以作用点在杠杆上 动力、阻力的方向不一定相反,但它们使杠杆转动的方向相反
2.杠杆的分类
特征 特点 应用举例
省力 杠杆 动力臂________ 阻力臂 省力、费 距离 撬棒、铡刀、动滑轮、轮轴、羊角锤、钢丝钳、手推车、花枝剪刀
费力 杠杆 动力臂________ 阻力臂 费力、省 距离 缝纫机踏板、起重臂、人的前臂、理发剪刀、钓鱼竿
等臂 杠杆 动力臂________ 阻力臂 不省力、 不费力 天平、定滑轮
3.杠杆的平衡条件
(1)探究前调试:应调节杠杆两端的螺母,使杠杆在水平位置平衡。这样做的目的是:可以方便地从杠杆上量出力臂。
(2)探究结论:杠杆的平衡条件(或杠杆原理):
动力×动力臂=阻力×阻力臂。
公式:F1l1=F2l2或=。
思考:利用杠杆原理进行计算时的步骤是什么?
常见题型的讲解
一.杠杆类型的判断
例1.如下图所示的工具,在使用中属于费力杠杆的是( )
例2.如图所示,下列器件中属于省力杠杆的是( )
二. 杠杆计算的掌握
类型一. 杠杆基础计算
例1.俯卧撑运动对发展力量素质,提高人体生理机能,发展平衡和支撑能力起着重要作用。可以改善中枢神经系统,有利于骨的坚实,关节的灵活,韧带的牢固,肌肉的粗壮及弹性,同时能加速血液循环,增大肺活量。如图所示,某同学在做俯卧撑运动,可将他视为一个杠杆:
(1)此杠杆的支点为 (选填 “O”、“ A”或 “B”)点。
(2)若该同学质量为50千克,那么他将身体撑起,每只手受到支持力至少为多少牛?若他在1min内做了30个俯卧撑,每次肩部上升的距离均为0.4m,则他的功率至少为多少瓦特?
(3)做俯卧撑运动时,该同学消耗的化学能 (选填“大于”、“等于”或“小于”)克服自身重所需的能量
例2.假期里,小兰和爸爸、妈妈一起参加了一个家庭游戏活动。活动要求是:家庭成员中的任意两名成员分别站在如图15所示的木板上,恰好使木板水平平衡。
(1)若小兰和爸爸的体重分别为400N和800N,小兰站在距离中央支点2m的一侧,爸爸应站在距离支点多远处才能使木板水平平衡?
(2)若小兰和爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,小兰的速度是0.5m/s,爸爸的速度是多大才能使木板水平平衡不被破坏?
图15
类型二 杠杆与压强类题型
例1.金属块M静置于水平地面上时,对地面的压强为5.4×105Pa。轻质杠杆AB的支点为O,OA:OB=5:3,在杠杆的B端用轻绳与金属块连接。若在杠杆的A端悬挂质量为4Kg的物体时,杠杆在水平位置平衡,此时金属块对地面的压强为1.8×105Pa.若要使金属块离开地面,那么杠杆A端所挂物体的质量至少应为多少?
变式训练
把正方体放在水平地面上,其对地面的压强为5.4×105Pa。AB是重力可忽略不计的杠杆,O为支点,且OA:OB?=1:2。将正方体挂在杠杆的A端,在B端施加180N竖直向下的拉力时,杠杆在水平位置平衡,如图所示,此时正方体对地面的压强变为1.8×105Pa。求:
(1)正方体的重力,
(2)正方体与地面的接触面积,
(3)在杠杆B?端施加多大的竖直向下的拉力时,正方体对地面的压力刚好为零??
类型三 杠杆与浮力结合
例1.如图10所示,顶面带有光滑凹槽的轻质杠杆AB可以绕支点O转动,杠杆的A端用细
线沿竖直方向连接在地板上,OB=0.5m,在杠杆的B端悬挂一个密度为0.8×103kg/m3的圆柱
体M。地板上有一个盛满水的容器。在圆柱体M体积的1/3浸入水中时,从容器内溢出0.4N
的水,杠杆在水平位置平衡。此时让一个质量为200g的小球从B点沿凹槽向A端匀速运动,
经过4s的时间,系在A端细线的拉力恰好等于0N。若整个过程中杠杆始终保持水平
平衡,则小球的运动速度为m/s。(g取10N/kg)
例2.如图7所示,杠杆AB的A点挂边长为10cm的正方体C,B点挂体积为2000cm3实心小球
D,AO:OB=1:2,杠杆在水平位置平衡时,D静止在空中,C对水平地面的压强为p1;若将小
球D浸没在某种液体中(未接触到容器底),杠杆在水平位置平衡时,C对水平地面的压强
p2比 p1增大了4000Pa,A点受到竖直向下的拉力为10N,则下列选项正确的是(g取10N/kg)
A.小球D浸没在某种液体中受到的浮力为20N
B.小球D浸没在某种液体中受到的浮力为40N
C.该液体的密度是2.0×103 kg/m3
D.小球D的密度是1.0×103 kg/m3
变式训练
如图所示,花岗岩石块甲、乙体积之比为13? 2,将它们分别挂在轻质硬棒AB的两端,把
铁块甲浸没在水中时,硬棒恰能水平位置平衡。然后将甲石块从水中取出,拭干后浸没在液
体丙中,调节石块乙的位置到C处时,硬棒在水平位置再次平衡,且OC=2OA。(已知花岗岩
的密度ρ=2.6×103kg/m3)则下列说法正确的是:
A.AO?:OB =1?: 5
B.AO ?OB =1 ?: 4
C.液体丙的密度ρ液=1.6×103kg/m3
D.液体丙的密度ρ液=1.8×103kg/m3
桔槔是一种利用杠杆原理取水的机械。它前端用绳系一木桶,后端系一配重物。取水时可将前端按下,木桶盛满水后,借助配重,只要用较小的力上提,水桶就上来了。假定OC︰OD=4:1,杆CD的质量不计,配重A的质量为3千克,密度为0.8×103(ρ<ρ水,密度不发生变化)的圆柱形木桶的质量为2千克,装满水后水的质量为13千克。为了用桔槔提升装满水的木桶,求:
(1)在水桶露出水面前,提水人至少需要用多大的力?
(2)在提出水面后,提水人至少需要用多大的力?
四. 杠杆的动态平衡
类型一 不变,变化
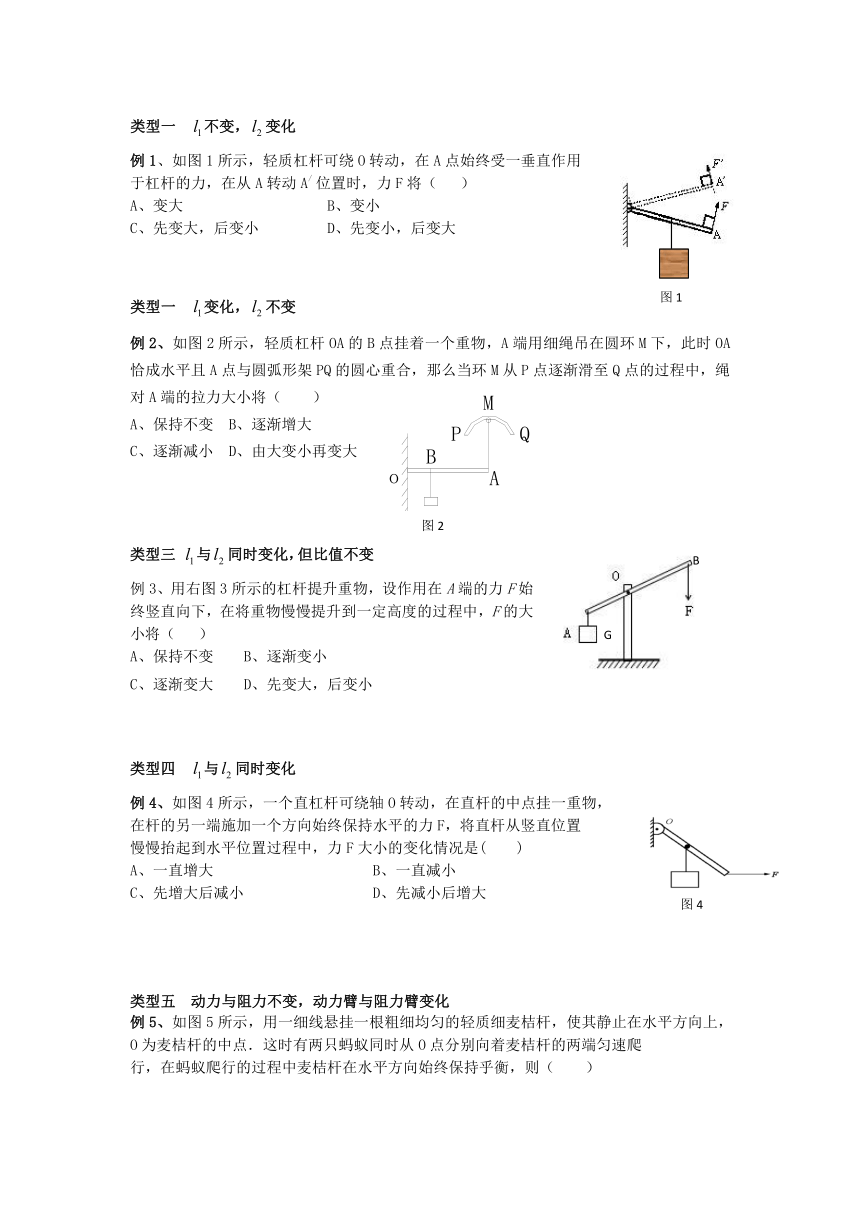
例1、如图1所示,轻质杠杆可绕O转动,在A点始终受一垂直作用
于杠杆的力,在从A转动A/ 位置时,力F将( )
A、变大 B、变小
C、先变大,后变小 D、先变小,后变大
类型一 变化,不变
例2、如图2所示,轻质杠杆OA的B点挂着一个重物,A端用细绳吊在圆环M下,此时OA恰成水平且A点与圆弧形架PQ的圆心重合,那么当环M从P点逐渐滑至Q点的过程中,绳对A端的拉力大小将( )
A、保持不变 B、逐渐增大
C、逐渐减小 D、由大变小再变大
类型三 与同时变化,但比值不变
例3、用右图3所示的杠杆提升重物,设作用在A端的力F始终竖直向下,在将重物慢慢提升到一定高度的过程中,F的大小将( )
A、保持不变 B、逐渐变小
C、逐渐变大 D、先变大,后变小
类型四 与同时变化
例4、如图4所示,一个直杠杆可绕轴O转动,在直杆的中点挂一重物,
在杆的另一端施加一个方向始终保持水平的力F,将直杆从竖直位置
慢慢抬起到水平位置过程中,力F大小的变化情况是( )
A、一直增大 B、一直减小
C、先增大后减小 D、先减小后增大
类型五 动力与阻力不变,动力臂与阻力臂变化
例5、如图5所示,用一细线悬挂一根粗细均匀的轻质细麦桔杆,使其静止在水平方向上,
O为麦桔杆的中点.这时有两只蚂蚁同时从O点分别向着麦桔杆的两端匀速爬
行,在蚂蚁爬行的过程中麦桔杆在水平方向始终保持乎衡,则( )
A、两蚂蚁的质量一定相等
B、两蚂蚁的爬行速度大小一定相等
C、两蚂蚁的质量与爬行速度大小的乘积一定相等
D、两蚂蚁对麦桔杆的压力一定相等
类型六 动力臂与阻力臂不变,动力与阻力改变
例6、如图6所示的轻质杠杆,AO小于BO.在A、B两端悬挂重物(同种物质)G1和G2后杠杆平衡.若将G1和G2同时浸没到水中则( )
A、杠杆仍保持平衡 B、杠杆的A端向下倾斜
C、 杠杆的B端向下倾斜 D、无法判断
变式有二
变式训练
1.如图所示,杠杆在物体A和力F作用下处于平衡,现在将力F方向改为沿虚线方向,要使杠杆仍保持平衡,必须是( )
A、F减小 B、F大小不变 C、F变大 D、F小于物体重力
2.一把粗细均匀的杠杆AB,在端点A、B处分别作用竖直向下的力F1、F2时,杠杆在水平位
置处于平衡。若使力F1、F2同时各减少2N,则杠杆失去平衡,且A端上升,B端下降,由此
可以判断杠杆AB的支点位置是( )
在杠杆的中点 B.不在杠杆的中点,而且靠近B端
C.不在杠杆的中点,而且靠近A端 D.无法确定
3.如图所示,轻质杠杆OA的中点悬挂一重G=60N的物
体,在A端施加一竖直向上的力F,杠杆在水平位置平
衡,则F= N。保持F的方向不变,在将杠杆从
A位置匀速提到B位置的过程中,力F将 (变
大/不变/变小)
4. 一根长为L,重为G的粗细均匀木棒,当支点在中点时刚好平衡.如果把左端锯下全长的,并叠放到左端剩余部分上面,则杠杆将为( )
A. 仍能平衡 B. 不能平衡,左端下沉 C. 无法判断
5.一个原来水平静止的杠杆,如果再作用一个力后,杠杆仍能处于静止状态,则此力可能是( )
A. 竖直作用于动力点上
B. 竖直作用于阻力点上
C. 竖直作用在支点上
D. 作用在杠杆的任一点,但力的作用线必须与杠杆垂直
一位瓜农用1.2米的扁担挑一担西瓜,前面一筐瓜重350牛,后面一筐重250牛.他的肩应放在扁担的什么位置,扁担才能平衡?若前后筐各减少50牛的瓜,肩应在什么位置扁担才能保持平衡?(扁担及筐的重力不计)
五.杠杆实验题
1.在完成教材中“探究杠杆的平衡条件”实验,得到杠杆平衡条件后.
(1)实验小组想再次验证结论是否正确,如图甲在A 位置挂4个钩码,按照结论计算可知在右边刻度6处挂2个钩码杠杆就能平衡.
(2)如图乙所示,小明想知道将刻度4位置的弹簧测力计由竖直向下拉改为倾斜向下拉会是什么情况.经小组讨论认为:根据杠杆平衡条件,测力计示 数相比竖直向下拉会__________(填“变大”、“变小”或“不变”),并且不便于测量_______·
(3)小华想到若铁架台不是在水平桌面上,而是在略微倾斜的桌面上是否影响实验呢?经小组分析不在水平桌面上___________(填“影响”或“不影响”)实验过程。
2.用如图所示的实验装置测量杠杆的机械效率,实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数F为________N,钩码总重G为1.0 N,钩码上升高度h为0.1 m,测力计移动距离s为0.3 m,则杠杆的机械效率为_______%。请写出使用该杠杆做额外功的一个原因:____________;
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到如表所示的两组数据:
次数 钩码悬挂点 钩码总量G/N 钩码移动距离h/m 拉力F/N 测力计移动距离s/m 机械效率η%
1 A点 1.5 0.10 0.7 0.30 71.4
2 B点 2.0 0.15 1.2 0.30 83.3
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论? 答:__________;请简要说明理由:_________________。(至少写一个)
3.如图甲所示,某同学做“研究杠杆的平衡条件”实验时,进行了以下操作:
(1)调节杠杆的左右螺母,使杠杆保持水平;
(2)在杠杆O点位置两边分别挂上数目不等的钩码,通过移动钩码位置,并调节杠杆两端的螺母,使杠杆重新保持水平,记录有关数据;
(3)改变两边钩码的数量,按照(2)再进行一次操作.
①指出该同学操作中存在的问题: .
②实验中使杠杆保持水平平衡的目的是: .
③实验中得到的结论是: .
④若右端不挂钩码,而改用弹簧秤拉如图乙,弹簧秤示数为F1,则F1×OA G×OB.(选填“大于”、“小于”或“等于”)
课后作业
1.图10所示的装置,杠杆自重不计,甲、乙是两个圆柱体,2ρ甲=3ρ乙,3V甲=4V乙,物体M的质量是80kg。只将圆柱体甲挂在杠杆B端时,杠杆在水平位置平衡,物体M对水平地面的压强为2000Pa;只将圆柱体乙挂在杠杆C点时,杠杆在水平位置平衡,物体M对水平地面的压强为3000Pa。若乙的体积为3×10-3m3,OA∶OB=2∶3,OA∶OC=2∶1,g取10N/kg,则甲的密度是 kg/m3。
2.质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是8N。然后在O点的正上方放一质量为0.5kg的小球,若小球以20cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零。(取g=10N/kg,绳的重力不计)
3.在菜市场内个别商贩会违反公平交易的原则,使用杆秤时通过不正当方式侵犯了消费者的合法权益.例如某标准杆秤的秤砣质量为1千克,秤和秤盘的总质量为0.5千克,O点为提纽悬点,A点为零刻度点,=3厘米,=9厘米,如图22所示.如换取了一个质量为0.7千克的秤砣,售出3.0千克的物品,消费者得到的物品实际质量()
A.2.0千克 B.2.3千克 C.2.5千克 D.2.8千克
4.在研究杠杆平衡条件的实验中:
(1)实验前,发现杠杆处于如图所示的状态,为了使杠杆在水平位置平衡,应将杠杆右端的平衡螺母向_____________(选填“右”或“左”)移动。
(2)上面操作使杠杆在水平位置平衡,这样做的目的是_____________________。
(3)某实验小组进行正确的实验操作后,得到的数据为F1=6N,L1=20cm,F2=4N和L2=30cm。该实验小组是否根据这组数据就能得出探究结论?___________;理由是____________________________________________________________。
5.如图所示为小明自制的风力板,口板为迎风板,其迎风面承受风力,b板为压重板,它水平放置,m为压重板上的铁板(a、b板重力不计)。当压重板上铁板重力一定时,风力大到一定程度,风力板就会倾倒,在这过程中,风对迎风板的作用力当作动力,_________当作阻力,压重板上的铁板越重,风力板倾倒时记录的风力越___________.
小明通过查阅资料和实验,在压重板上加上重力不同的铁板,制成能测风力1~8级的8个风力板,构成一套风力探测仪。在南风盛行的某地,小明用这套风力探测仪测定当天最强的风力。
(1)在开阔地的水平地面放置风力探测仪时,小明应____________________.
(2)小明确定当天最强风力的方法是
_____________________________________.
图10
O
B
A
M
O
图7
B
A
D
C
图1
图2
B
G
图4
图5
图6
M
O
A
B
乙
甲
C
图10
1.杠杆基本知识
简图
定义 在力的作用下绕着________转动的硬棒叫杠杆
五要素 支点 杠杆绕着转动的点,一般用字母O表示
动力 使杠杆转动的力,一般用字母F1 表示
阻力 阻碍杠杆转动的力,一般用字母F2 表示
动力臂 从支点到动力作用线的距离,一般用字母l1表示
阻力臂 从支点到阻力作用线的距离,一般用字母l2表示
说明 动力、阻力都是杠杆受的力,所以作用点在杠杆上 动力、阻力的方向不一定相反,但它们使杠杆转动的方向相反
2.杠杆的分类
特征 特点 应用举例
省力 杠杆 动力臂________ 阻力臂 省力、费 距离 撬棒、铡刀、动滑轮、轮轴、羊角锤、钢丝钳、手推车、花枝剪刀
费力 杠杆 动力臂________ 阻力臂 费力、省 距离 缝纫机踏板、起重臂、人的前臂、理发剪刀、钓鱼竿
等臂 杠杆 动力臂________ 阻力臂 不省力、 不费力 天平、定滑轮
3.杠杆的平衡条件
(1)探究前调试:应调节杠杆两端的螺母,使杠杆在水平位置平衡。这样做的目的是:可以方便地从杠杆上量出力臂。
(2)探究结论:杠杆的平衡条件(或杠杆原理):
动力×动力臂=阻力×阻力臂。
公式:F1l1=F2l2或=。
思考:利用杠杆原理进行计算时的步骤是什么?
常见题型的讲解
一.杠杆类型的判断
例1.如下图所示的工具,在使用中属于费力杠杆的是( )
例2.如图所示,下列器件中属于省力杠杆的是( )
二. 杠杆计算的掌握
类型一. 杠杆基础计算
例1.俯卧撑运动对发展力量素质,提高人体生理机能,发展平衡和支撑能力起着重要作用。可以改善中枢神经系统,有利于骨的坚实,关节的灵活,韧带的牢固,肌肉的粗壮及弹性,同时能加速血液循环,增大肺活量。如图所示,某同学在做俯卧撑运动,可将他视为一个杠杆:
(1)此杠杆的支点为 (选填 “O”、“ A”或 “B”)点。
(2)若该同学质量为50千克,那么他将身体撑起,每只手受到支持力至少为多少牛?若他在1min内做了30个俯卧撑,每次肩部上升的距离均为0.4m,则他的功率至少为多少瓦特?
(3)做俯卧撑运动时,该同学消耗的化学能 (选填“大于”、“等于”或“小于”)克服自身重所需的能量
例2.假期里,小兰和爸爸、妈妈一起参加了一个家庭游戏活动。活动要求是:家庭成员中的任意两名成员分别站在如图15所示的木板上,恰好使木板水平平衡。
(1)若小兰和爸爸的体重分别为400N和800N,小兰站在距离中央支点2m的一侧,爸爸应站在距离支点多远处才能使木板水平平衡?
(2)若小兰和爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,小兰的速度是0.5m/s,爸爸的速度是多大才能使木板水平平衡不被破坏?
图15
类型二 杠杆与压强类题型
例1.金属块M静置于水平地面上时,对地面的压强为5.4×105Pa。轻质杠杆AB的支点为O,OA:OB=5:3,在杠杆的B端用轻绳与金属块连接。若在杠杆的A端悬挂质量为4Kg的物体时,杠杆在水平位置平衡,此时金属块对地面的压强为1.8×105Pa.若要使金属块离开地面,那么杠杆A端所挂物体的质量至少应为多少?
变式训练
把正方体放在水平地面上,其对地面的压强为5.4×105Pa。AB是重力可忽略不计的杠杆,O为支点,且OA:OB?=1:2。将正方体挂在杠杆的A端,在B端施加180N竖直向下的拉力时,杠杆在水平位置平衡,如图所示,此时正方体对地面的压强变为1.8×105Pa。求:
(1)正方体的重力,
(2)正方体与地面的接触面积,
(3)在杠杆B?端施加多大的竖直向下的拉力时,正方体对地面的压力刚好为零??
类型三 杠杆与浮力结合
例1.如图10所示,顶面带有光滑凹槽的轻质杠杆AB可以绕支点O转动,杠杆的A端用细
线沿竖直方向连接在地板上,OB=0.5m,在杠杆的B端悬挂一个密度为0.8×103kg/m3的圆柱
体M。地板上有一个盛满水的容器。在圆柱体M体积的1/3浸入水中时,从容器内溢出0.4N
的水,杠杆在水平位置平衡。此时让一个质量为200g的小球从B点沿凹槽向A端匀速运动,
经过4s的时间,系在A端细线的拉力恰好等于0N。若整个过程中杠杆始终保持水平
平衡,则小球的运动速度为m/s。(g取10N/kg)
例2.如图7所示,杠杆AB的A点挂边长为10cm的正方体C,B点挂体积为2000cm3实心小球
D,AO:OB=1:2,杠杆在水平位置平衡时,D静止在空中,C对水平地面的压强为p1;若将小
球D浸没在某种液体中(未接触到容器底),杠杆在水平位置平衡时,C对水平地面的压强
p2比 p1增大了4000Pa,A点受到竖直向下的拉力为10N,则下列选项正确的是(g取10N/kg)
A.小球D浸没在某种液体中受到的浮力为20N
B.小球D浸没在某种液体中受到的浮力为40N
C.该液体的密度是2.0×103 kg/m3
D.小球D的密度是1.0×103 kg/m3
变式训练
如图所示,花岗岩石块甲、乙体积之比为13? 2,将它们分别挂在轻质硬棒AB的两端,把
铁块甲浸没在水中时,硬棒恰能水平位置平衡。然后将甲石块从水中取出,拭干后浸没在液
体丙中,调节石块乙的位置到C处时,硬棒在水平位置再次平衡,且OC=2OA。(已知花岗岩
的密度ρ=2.6×103kg/m3)则下列说法正确的是:
A.AO?:OB =1?: 5
B.AO ?OB =1 ?: 4
C.液体丙的密度ρ液=1.6×103kg/m3
D.液体丙的密度ρ液=1.8×103kg/m3
桔槔是一种利用杠杆原理取水的机械。它前端用绳系一木桶,后端系一配重物。取水时可将前端按下,木桶盛满水后,借助配重,只要用较小的力上提,水桶就上来了。假定OC︰OD=4:1,杆CD的质量不计,配重A的质量为3千克,密度为0.8×103(ρ<ρ水,密度不发生变化)的圆柱形木桶的质量为2千克,装满水后水的质量为13千克。为了用桔槔提升装满水的木桶,求:
(1)在水桶露出水面前,提水人至少需要用多大的力?
(2)在提出水面后,提水人至少需要用多大的力?
四. 杠杆的动态平衡
类型一 不变,变化
例1、如图1所示,轻质杠杆可绕O转动,在A点始终受一垂直作用
于杠杆的力,在从A转动A/ 位置时,力F将( )
A、变大 B、变小
C、先变大,后变小 D、先变小,后变大
类型一 变化,不变
例2、如图2所示,轻质杠杆OA的B点挂着一个重物,A端用细绳吊在圆环M下,此时OA恰成水平且A点与圆弧形架PQ的圆心重合,那么当环M从P点逐渐滑至Q点的过程中,绳对A端的拉力大小将( )
A、保持不变 B、逐渐增大
C、逐渐减小 D、由大变小再变大
类型三 与同时变化,但比值不变
例3、用右图3所示的杠杆提升重物,设作用在A端的力F始终竖直向下,在将重物慢慢提升到一定高度的过程中,F的大小将( )
A、保持不变 B、逐渐变小
C、逐渐变大 D、先变大,后变小
类型四 与同时变化
例4、如图4所示,一个直杠杆可绕轴O转动,在直杆的中点挂一重物,
在杆的另一端施加一个方向始终保持水平的力F,将直杆从竖直位置
慢慢抬起到水平位置过程中,力F大小的变化情况是( )
A、一直增大 B、一直减小
C、先增大后减小 D、先减小后增大
类型五 动力与阻力不变,动力臂与阻力臂变化
例5、如图5所示,用一细线悬挂一根粗细均匀的轻质细麦桔杆,使其静止在水平方向上,
O为麦桔杆的中点.这时有两只蚂蚁同时从O点分别向着麦桔杆的两端匀速爬
行,在蚂蚁爬行的过程中麦桔杆在水平方向始终保持乎衡,则( )
A、两蚂蚁的质量一定相等
B、两蚂蚁的爬行速度大小一定相等
C、两蚂蚁的质量与爬行速度大小的乘积一定相等
D、两蚂蚁对麦桔杆的压力一定相等
类型六 动力臂与阻力臂不变,动力与阻力改变
例6、如图6所示的轻质杠杆,AO小于BO.在A、B两端悬挂重物(同种物质)G1和G2后杠杆平衡.若将G1和G2同时浸没到水中则( )
A、杠杆仍保持平衡 B、杠杆的A端向下倾斜
C、 杠杆的B端向下倾斜 D、无法判断
变式有二
变式训练
1.如图所示,杠杆在物体A和力F作用下处于平衡,现在将力F方向改为沿虚线方向,要使杠杆仍保持平衡,必须是( )
A、F减小 B、F大小不变 C、F变大 D、F小于物体重力
2.一把粗细均匀的杠杆AB,在端点A、B处分别作用竖直向下的力F1、F2时,杠杆在水平位
置处于平衡。若使力F1、F2同时各减少2N,则杠杆失去平衡,且A端上升,B端下降,由此
可以判断杠杆AB的支点位置是( )
在杠杆的中点 B.不在杠杆的中点,而且靠近B端
C.不在杠杆的中点,而且靠近A端 D.无法确定
3.如图所示,轻质杠杆OA的中点悬挂一重G=60N的物
体,在A端施加一竖直向上的力F,杠杆在水平位置平
衡,则F= N。保持F的方向不变,在将杠杆从
A位置匀速提到B位置的过程中,力F将 (变
大/不变/变小)
4. 一根长为L,重为G的粗细均匀木棒,当支点在中点时刚好平衡.如果把左端锯下全长的,并叠放到左端剩余部分上面,则杠杆将为( )
A. 仍能平衡 B. 不能平衡,左端下沉 C. 无法判断
5.一个原来水平静止的杠杆,如果再作用一个力后,杠杆仍能处于静止状态,则此力可能是( )
A. 竖直作用于动力点上
B. 竖直作用于阻力点上
C. 竖直作用在支点上
D. 作用在杠杆的任一点,但力的作用线必须与杠杆垂直
一位瓜农用1.2米的扁担挑一担西瓜,前面一筐瓜重350牛,后面一筐重250牛.他的肩应放在扁担的什么位置,扁担才能平衡?若前后筐各减少50牛的瓜,肩应在什么位置扁担才能保持平衡?(扁担及筐的重力不计)
五.杠杆实验题
1.在完成教材中“探究杠杆的平衡条件”实验,得到杠杆平衡条件后.
(1)实验小组想再次验证结论是否正确,如图甲在A 位置挂4个钩码,按照结论计算可知在右边刻度6处挂2个钩码杠杆就能平衡.
(2)如图乙所示,小明想知道将刻度4位置的弹簧测力计由竖直向下拉改为倾斜向下拉会是什么情况.经小组讨论认为:根据杠杆平衡条件,测力计示 数相比竖直向下拉会__________(填“变大”、“变小”或“不变”),并且不便于测量_______·
(3)小华想到若铁架台不是在水平桌面上,而是在略微倾斜的桌面上是否影响实验呢?经小组分析不在水平桌面上___________(填“影响”或“不影响”)实验过程。
2.用如图所示的实验装置测量杠杆的机械效率,实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数F为________N,钩码总重G为1.0 N,钩码上升高度h为0.1 m,测力计移动距离s为0.3 m,则杠杆的机械效率为_______%。请写出使用该杠杆做额外功的一个原因:____________;
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到如表所示的两组数据:
次数 钩码悬挂点 钩码总量G/N 钩码移动距离h/m 拉力F/N 测力计移动距离s/m 机械效率η%
1 A点 1.5 0.10 0.7 0.30 71.4
2 B点 2.0 0.15 1.2 0.30 83.3
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论? 答:__________;请简要说明理由:_________________。(至少写一个)
3.如图甲所示,某同学做“研究杠杆的平衡条件”实验时,进行了以下操作:
(1)调节杠杆的左右螺母,使杠杆保持水平;
(2)在杠杆O点位置两边分别挂上数目不等的钩码,通过移动钩码位置,并调节杠杆两端的螺母,使杠杆重新保持水平,记录有关数据;
(3)改变两边钩码的数量,按照(2)再进行一次操作.
①指出该同学操作中存在的问题: .
②实验中使杠杆保持水平平衡的目的是: .
③实验中得到的结论是: .
④若右端不挂钩码,而改用弹簧秤拉如图乙,弹簧秤示数为F1,则F1×OA G×OB.(选填“大于”、“小于”或“等于”)
课后作业
1.图10所示的装置,杠杆自重不计,甲、乙是两个圆柱体,2ρ甲=3ρ乙,3V甲=4V乙,物体M的质量是80kg。只将圆柱体甲挂在杠杆B端时,杠杆在水平位置平衡,物体M对水平地面的压强为2000Pa;只将圆柱体乙挂在杠杆C点时,杠杆在水平位置平衡,物体M对水平地面的压强为3000Pa。若乙的体积为3×10-3m3,OA∶OB=2∶3,OA∶OC=2∶1,g取10N/kg,则甲的密度是 kg/m3。
2.质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是8N。然后在O点的正上方放一质量为0.5kg的小球,若小球以20cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零。(取g=10N/kg,绳的重力不计)
3.在菜市场内个别商贩会违反公平交易的原则,使用杆秤时通过不正当方式侵犯了消费者的合法权益.例如某标准杆秤的秤砣质量为1千克,秤和秤盘的总质量为0.5千克,O点为提纽悬点,A点为零刻度点,=3厘米,=9厘米,如图22所示.如换取了一个质量为0.7千克的秤砣,售出3.0千克的物品,消费者得到的物品实际质量()
A.2.0千克 B.2.3千克 C.2.5千克 D.2.8千克
4.在研究杠杆平衡条件的实验中:
(1)实验前,发现杠杆处于如图所示的状态,为了使杠杆在水平位置平衡,应将杠杆右端的平衡螺母向_____________(选填“右”或“左”)移动。
(2)上面操作使杠杆在水平位置平衡,这样做的目的是_____________________。
(3)某实验小组进行正确的实验操作后,得到的数据为F1=6N,L1=20cm,F2=4N和L2=30cm。该实验小组是否根据这组数据就能得出探究结论?___________;理由是____________________________________________________________。
5.如图所示为小明自制的风力板,口板为迎风板,其迎风面承受风力,b板为压重板,它水平放置,m为压重板上的铁板(a、b板重力不计)。当压重板上铁板重力一定时,风力大到一定程度,风力板就会倾倒,在这过程中,风对迎风板的作用力当作动力,_________当作阻力,压重板上的铁板越重,风力板倾倒时记录的风力越___________.
小明通过查阅资料和实验,在压重板上加上重力不同的铁板,制成能测风力1~8级的8个风力板,构成一套风力探测仪。在南风盛行的某地,小明用这套风力探测仪测定当天最强的风力。
(1)在开阔地的水平地面放置风力探测仪时,小明应____________________.
(2)小明确定当天最强风力的方法是
_____________________________________.
图10
O
B
A
M
O
图7
B
A
D
C
图1
图2
B
G
图4
图5
图6
M
O
A
B
乙
甲
C
图10
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
