2018-2019学年辽宁省朝阳市凌源二中高三(上)期末物理试卷 Word版含解析
文档属性
| 名称 | 2018-2019学年辽宁省朝阳市凌源二中高三(上)期末物理试卷 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 513.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-06-27 00:00:00 | ||
图片预览



文档简介
2018-2019学年辽宁省朝阳市凌源二中高三(上)期末物理试卷
一.选择题(本题共12题,共40分.其中第1-8题只有一个选项正确,每小题3分;第9-12有多个选项正确,每小题3分,全部选对得4分,选对但不全得2分,有选错得0分)
1.(3分)下列关于物理学史和物理研究方法的叙述中,正确的是( )
A.用点电荷来代替带电体的研究方法叫微元法
B.伽利略借助实验研究和逻辑推理得出了自由落体运动规律
C.利用v﹣t图象推导匀变速直线运动位移公式的方法是理想模型法
D.法拉第发现电流的磁效应与他坚信电和磁之间一定存在联系的哲学思想是分不开的
2.(3分)如图所示,在粗糙水平面上放置A、B、C、D四个小物块,各小物块之间由四根完全相同的轻弹簧相互连接,正好组成一个菱形,∠BAD=120°,整个系统保持静止状态.已知A物块所受的摩擦力大小为f,则D物块所受的摩擦力大小为( )
A.f B.f C.f D.2 f
3.(3分)质量为2kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.重力加速度g取10m/s2,则物体在t=0至t=12s这段时间的位移大小为( )
A.18 m B.54 m C.72 m D.198 m
4.(3分)如图所示,水平面上固定有一个斜面,从斜面顶端向右平抛一只小球,当初速度为v0时,小球恰好落到斜面底端,平抛的飞行时间为t0.现用不同的初速度v从该斜面顶端向右平抛这只小球,以下哪个图象能正确表示平抛的飞行时间t随v变化的函数关系( )
A. B.
C. D.
5.(3分)如图所示,内壁光滑的半球形碗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则( )
A.球A的角速度小于球B的角速度
B.球A的线速度小于球B的线速度
C.球A对碗壁的压力等于球B对碗壁的压力
D.球A的向心加速度大于球B的向心加速度
6.(3分)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的平均密度ρ=
C.月球的第一宇宙速度v=
D.月球的质量m月=
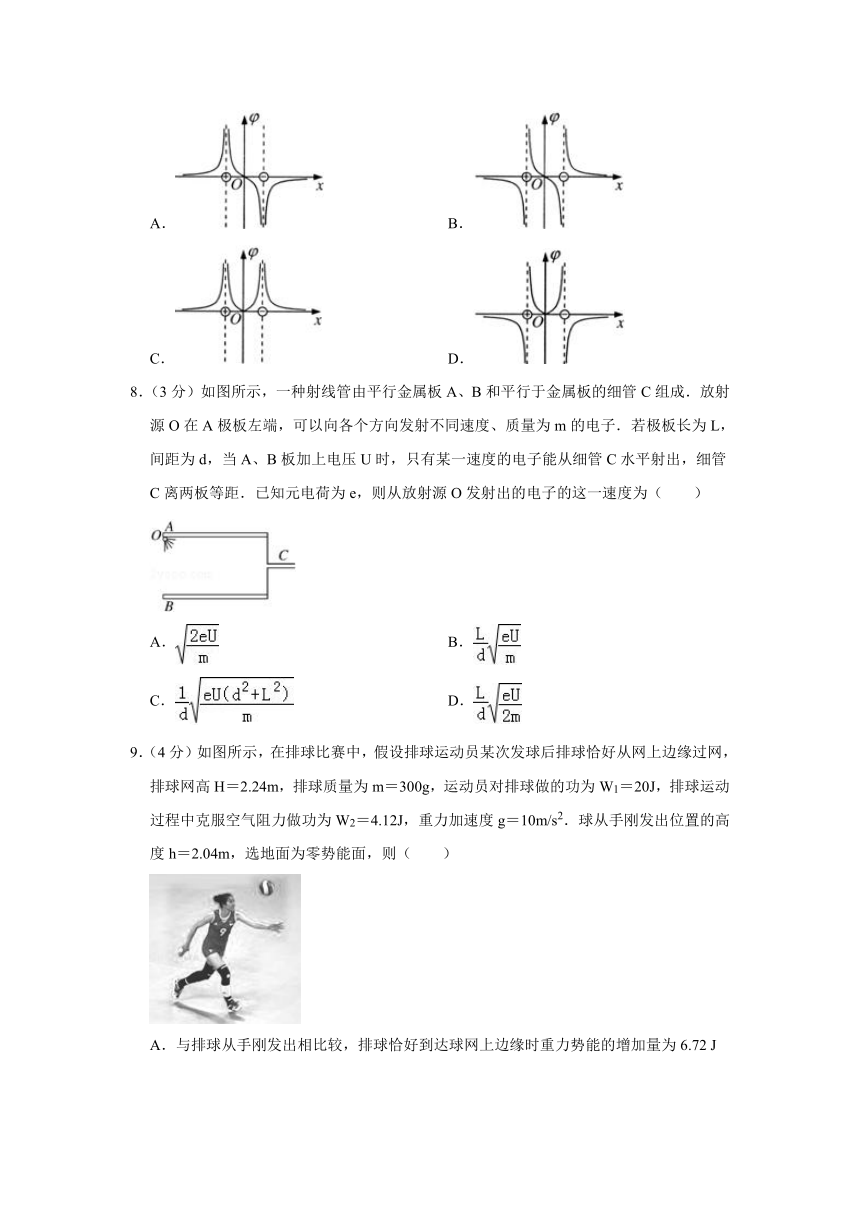
7.(3分)两个等量异种点电荷位于x轴上,相对原点对称分布,正确描述电势φ随位置x变化规律的是图( )
A. B.
C. D.
8.(3分)如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速度、质量为m的电子.若极板长为L,间距为d,当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离两板等距.已知元电荷为e,则从放射源O发射出的电子的这一速度为( )
A. B.
C. D.
9.(4分)如图所示,在排球比赛中,假设排球运动员某次发球后排球恰好从网上边缘过网,排球网高H=2.24m,排球质量为m=300g,运动员对排球做的功为W1=20J,排球运动过程中克服空气阻力做功为W2=4.12J,重力加速度g=10m/s2.球从手刚发出位置的高度h=2.04m,选地面为零势能面,则( )
A.与排球从手刚发出相比较,排球恰好到达球网上边缘时重力势能的增加量为6.72 J
B.排球恰好到达球网上边缘时的机械能为22 J
C.排球恰好到达球网上边缘时的动能为15.88 J
D.与排球从手刚发出相比较,排球恰好到达球网上边缘时动能的减少量为4.72 J
10.(4分)如图所示为通过弹射器研究轻弹簧的弹性势能的实验装置.半径为R的光滑圆形轨道竖直固定于光滑水平面上并与水平地面相切于B点,弹射器固定于A处.某次实验过程中弹射器射出一质量为m的小球,恰能沿圆轨道内侧到达最髙点C,然后从轨道D处(D与圆心等高)下落至水平面.忽略空气阻力,取重力加速度为g.下列说法正确的是( )
A.小球从D处下落至水平面的时间小于
B.小球运动至最低点B时对轨道压力为5mg
C.小球落至水平面时的动能为2mgR
D.释放小球前弹射器的弹性势能为
11.(4分)如图所示,有一范围足够大的水平匀强磁场,磁感应强度为B,一个质量为m,电荷量为+q的带电小圆环套在一根固定的绝缘竖直长杆上,环与杆间的动摩擦因数为μ,现使圆环以初速度v0向上运动,经时间t0圆环回到出发点,不计空气阻力,取竖直向上为正方向,下列描述该过程中圆环的速度v随时间t、摩擦力f随时间t、动能Et随位移x、机械能E随位移x变化规律的图象中,可能正确的是( )
A. B.
C. D.
12.(4分)在光滑的足够长的斜面上横放一电阻可忽略不计的金属杆,如图所示,让金属杆从静止向下运动一段时间.已知此时间内重力做了W1的功,金属杆克服安培力做了W2的功,下列关于此过程的讲法正确的是( )
A.此过程中动能增加了(W1﹣W2)
B.此过程中机械能增加了(W1﹣W2)
C.此过程中重力势能减少了W1
D.此过程中回路中产生了W2的电能
二.填空题:(2个小题,共12分)
13.(4分)“验证机械能守恒定律”的实验可以采用如图l所示的(甲)或(乙)方案来进行.
(1)比较这两种方案, (填“甲”或“乙”)方案好些,理由是 .
(2)如图2是采用(甲)方案时得到的一条纸带,在计算图中N点速度时,几位同学分别用下列不同的方法进行,其中正确的是
A.vN=gnT
B.vN=
C.vN=
D.vN=g(n﹣1)T.
14.(8分)小明同学想测量一节旧干电池的电动势和内电阻,身边仅有下列器材:一个多用电表、一个定值电阻R1、一个滑动变阻器R2(0~20Ω)、一个开关S、导线若干.小明设计了实验原理图(如图甲所示),并进行了如下实验:
①根据原理图,连接实验器材,且S断开;
②多用电表选择“R×1”挡,先 ,后用红表笔接a端,黑表笔接b端,记录下R1示数(如图乙所示);
③S闭合,多用电表选择“直流电压2.5V”挡, 表笔接a端, 表笔接b端(选填“红”或“黑”),记录下示数U1;然后再测出b、c间的电压,记录下示数U2;
④调节滑动变阻器,重复步骤③,得到如下表所示的6组数据;
U1/V
0.10
0.20
0.30
0.40
0.50
0.60
U2/V
1.05
0.90
0.75
0.70
0.45
0.30
(1)请你完成上述操作步骤中的三处填空;
(2)由图乙可知R1测量值为 Ω;
(3)请在如图丙所示的坐标纸中画出U2﹣U1关系图;
(4)该电池的内电阻为 Ω.(保留两位有效数字)
三.计算题:(3个小题,共33分)
15.(9分)如图所示,在倾角为30°的光滑斜面上,一劲度系数为K=200N/m的轻质弹簧一端连接固定挡板C上,另一端连接一质量为m=4Kg的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端与质量也为m的物体B相连,细绳与斜面平行,斜面足够长,用手托住物体B使绳子刚好没有拉力,然后由静止释放,求:
(1)弹簧恢复原长时细绳上的拉力;
(2)物体A沿斜面向上运动多远时获得最大速度;
(3)物体A的最大速度大小.
16.(12分)如图所示,在平面直角坐标系xoy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从电场中Q(﹣2h,﹣h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子从Q点运动到N点的时间t.
17.(12分)如图所示,两平行导轨间距L=0.1m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角θ=30°,垂直斜面方向向上磁感应强度B=0.5T,水平部分没有磁场。金属棒ab质量m=0.005kg,电阻r=0.02Ω,运动中与导轨有良好接触,并且垂直于导轨,电阻R=0.08Ω,其余电阻不计,当金属棒从斜面上离地高h=1.0m以上任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25m.(取g=10m/s2),求:
(1)棒在斜面上的最大速度?
(2)水平面的滑动摩擦因数?
(3)从高度h=1.0m处滑下后电阻R上产生的热量?
选考题:共15分.请从给出的三道题中任选一题作答,如果多做,则按所做的第一题计分【选修3-3】(15分)
18.(5分)下列说法中正确的是( )
A.布朗运动并不是液体分子的运动,但它说明分子永不停息地做无规则运动
B.叶面上的小露珠呈球形是由于液体表面张力的作用
C.液晶显示器是利用了液晶对光具有各向异性的特点
D.当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小
19.(10分)如图所示,在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内,用4cm高的水银柱封闭着51cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg。
①若缓慢对玻璃管加热,当水银柱上表面与管口刚好相平时,求管中气体的温度;
②若保持管内温度始终为33℃,现将水银缓慢注入管中,直到水银柱上表面与管口相平,求此时管中气体的压强。
【选修3-4】(15分)
20.A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图中甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图中丙、丁所示,则A、B两列波的波速vA、vB之比可能是( )
A.1:1 B.2:1 C.1:2 D.3:1
E.1:3
21.有一玻璃球冠,右侧面镀银,光源S就在其对称轴上,如图所示,从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折射入玻璃球冠内,经右侧镀银面第一次反射恰能沿原路返回,若球面半径为R,玻璃折射率为,求光源S与球冠顶点M之间的距离SM为多大?
【选修3-5】(15分)
22.以下说法符合物理学史的是 ( )
A.普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元
B.康普顿效应表明光子具有能量
C.德布罗意把光的波粒二象性推广到实物粒子,认为实物粒子也具有波动性
D.汤姆逊通过α粒子散射实验,提出了原子具有核式结构
E.卢瑟福利用α粒子轰击氮核发现了质子,并预言了中子的存在
23.如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连。另一质量为m的小物块A以速度v0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计。(所有过程都在弹簧弹性限度范围内)求:
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比。
2018-2019学年辽宁省朝阳市凌源二中高三(上)期末物理试卷
参考答案与试题解析
一.选择题(本题共12题,共40分.其中第1-8题只有一个选项正确,每小题3分;第9-12有多个选项正确,每小题3分,全部选对得4分,选对但不全得2分,有选错得0分)
1.(3分)下列关于物理学史和物理研究方法的叙述中,正确的是( )
A.用点电荷来代替带电体的研究方法叫微元法
B.伽利略借助实验研究和逻辑推理得出了自由落体运动规律
C.利用v﹣t图象推导匀变速直线运动位移公式的方法是理想模型法
D.法拉第发现电流的磁效应与他坚信电和磁之间一定存在联系的哲学思想是分不开的
【分析】物理学中对于多因素(多变量)的问题,常常采用控制因素(变量)的方法,把多因素的问题变成多个单因素的问题;每一次只改变其中的某一个因素,而控制其余几个因素不变,从而研究被改变的这个因素对事物影响,分别加以研究,最后再综合解决,这种方法叫控制变量法;它是科学探究中的重要思想方法,控制变量法是初中物理中常用的探索问题和分析解决问题的科学方法之一.
等效替代法是指在研究某一个物理现象和规律中,因实验本身的特殊限制或因实验器材等限制,不可以或很难直接揭示物理本质,而采取与之相似或有共同特征的等效现象来替代的方法.
【解答】解:A、用质点代替实际物体是采用了理想模型的方法,质点实际不存在,故A错误;
B、伽利略在研究自由落体运动时采用了推理的方法,故B正确;
C、在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法,故C错误;
D、法拉第发现电磁感应现象,和他坚信电与磁之间一定存在着联系的哲学思想分不开,故D错误;
故选:B。
【点评】解决此题要知道常用的物理学研究方法:控制变量法、等效替代法、模型法、比较法、分类法、类比法、转换法等.
2.(3分)如图所示,在粗糙水平面上放置A、B、C、D四个小物块,各小物块之间由四根完全相同的轻弹簧相互连接,正好组成一个菱形,∠BAD=120°,整个系统保持静止状态.已知A物块所受的摩擦力大小为f,则D物块所受的摩擦力大小为( )
A.f B.f C.f D.2 f
【分析】物体在水平面上受弹簧弹力和静摩擦力平衡,根据力的合成方法求解弹簧的弹力.
【解答】解:已知A物块所受的摩擦力大小为f,设每根弹簧的弹力为F,则有:2Fcos60°=f,对D:2Fcos30°=f′,解得:f′=F=f
故选:C。
【点评】本题考查了物体受共点力平衡和力的合成计算,难度不大.
3.(3分)质量为2kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.重力加速度g取10m/s2,则物体在t=0至t=12s这段时间的位移大小为( )
A.18 m B.54 m C.72 m D.198 m
【分析】本题的关键是根据F﹣t图象分别对不同的时间段进行分析,注意0到3s时间内,由于物体受到的合力恰好为零,所以物体仍保持静止;第二段时间内,物体做匀加速直线运动,可根据牛顿运动定律求出位移;第三段时间内,物体做匀速直线运动,第四段时间内,物体做匀加速直线运动,根据运动学公式分别求出各段时间内的位移,然后相加即可.
【解答】解:对物体受力分析可知,0到3s内,由于滑动摩擦力为:==0.2×20N=4N,恰好等于外力F大小,所以物体仍能保持静止状态,
3到6s内,物体产生的加速度为:a==,发生的位移为:===9m
6到9s内,物体所受的合力为零,做匀速直线运动,由于6s时的速度为:v=at=2×3=6m/s,所以发生的位移为:=vt=6×(9﹣6)=18m
9到12s内,物体做匀加速直线运动,发生的位移为:=vt=6×3+=27m
所以总位移为:x=0=9+18+27=54m,所以B正确;
故选:B。
【点评】遇到多过程的动力学问题,应分别进行受力分析和运动过程分析,然后选取相应的物理规律进行求解,也可以借助v﹣t图象求解.
4.(3分)如图所示,水平面上固定有一个斜面,从斜面顶端向右平抛一只小球,当初速度为v0时,小球恰好落到斜面底端,平抛的飞行时间为t0.现用不同的初速度v从该斜面顶端向右平抛这只小球,以下哪个图象能正确表示平抛的飞行时间t随v变化的函数关系( )
A. B.
C. D.
【分析】根据小球落在斜面上,结合竖直位移与水平位移的关系求出运动的时间.小球落在地面上,高度一定,则运动时间一定.
【解答】解:当小球落在斜面上时,有:tanθ=,解得t=,与速度v成正比。
当小球落在地面上,根据h=得,t=,知运动时间不变。可知t与v的关系图线先是过原点的一条倾斜直线,然后是平行于横轴的直线。故C正确,A、B、D错误。
故选:C。
【点评】解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.
5.(3分)如图所示,内壁光滑的半球形碗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则( )
A.球A的角速度小于球B的角速度
B.球A的线速度小于球B的线速度
C.球A对碗壁的压力等于球B对碗壁的压力
D.球A的向心加速度大于球B的向心加速度
【分析】球受重力和支持力,靠重力和支持力的合力提供圆周运动的向心力,根据F合=ma=═mrω2,比较线速度、角速度和向心加速度的大小.并比较支持力的大小,从而能比较压力的大小.
【解答】解:ABD、对于任意一球,设其轨道处半球形碗的半径与竖直方向的夹角为θ,半球形碗的半径为R.根据重力和支持力的合力提供圆周运动的向心力,得:
F合=mgtanθ=ma==mrω2
又 r=Rsinθ
联立得:v=,a=gtanθ,
R一定,可知θ越大,线速度v越大、角速度ω越大、向心加速度a越大,所以球A的线速度大于球B的线速度,球A的角速度大于球B的角速度,球A的向心加速度大于球B的向心加速度。故AB错误,D正确。
C、受力分析可知:球所受的支持力FN=,θ越大,FN越大,则碗对A球的支持力较大,由牛顿第三定律知球A对碗壁的压力大于球B对碗壁的压力,C错误。
故选:D。
【点评】解决本题的关键知道小球做匀速圆周运动,靠重力和支持力的合力提供向心力,能灵活选择向心力的公式,由牛顿运动定律列式分析.
6.(3分)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的平均密度ρ=
C.月球的第一宇宙速度v=
D.月球的质量m月=
【分析】宇航员在月球上自高h处以初速度v0水平抛出一物体,测出物体的水平射程为L,根据水平射程和初速度求出运动的时间,
根据h=gt2求出月球表面的重力加速度大小;由g=求得月球的质量;根据重力提供向心力求出卫星的第一宇宙速度;由质量与半径可求得平均密度。
【解答】解:A、平抛运动的时间t=.再根据h=gt2,得g月=,故A错误;
B、由g月= 与g月=,可得:m月=,因此月球的平均密度ρ==.故B正确。
C、第一宇宙速度:v===,故C错误;
D、由g月= 与g月=,可得:m月=,故D错误;
故选:B。
【点评】解决本题的关键知道平抛运动在水平方向上和竖直方向上的运动规律,以及掌握万有引力提供向心力以及万有引力等于重力这两个理论的运用。
7.(3分)两个等量异种点电荷位于x轴上,相对原点对称分布,正确描述电势φ随位置x变化规律的是图( )
A. B.
C. D.
【分析】本题根据电场线的性质,沿电场线的方向电势降低进行判断即可。
【解答】解:两个等量异号电荷的电场线如下图,
根据“沿电场线方向电势降低”的原理,从左侧无穷远处向右电势应升高,正电荷所在位置处最高;然后再慢慢减小,O点处电势为零,则O点右侧电势为负,同理到达负电荷时电势最小,经过负电荷后,电势开始升高,直到无穷远处,电势为零;故B、C、D是错误的;A正确。
故选:A。
【点评】本题中应明确沿电场线的方向电势降低;并且异号电荷连线的中垂线上的电势为零;因为其中垂线为等势面,与无穷远处电势相等。
8.(3分)如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速度、质量为m的电子.若极板长为L,间距为d,当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离两板等距.已知元电荷为e,则从放射源O发射出的电子的这一速度为( )
A. B.
C. D.
【分析】当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,逆过来看,该粒子做类平抛运动,通过类平抛运动求出粒子的末速度,即为放射源O发射出的电子的速度.
【解答】解:将从细管C水平射出的电子逆过来看,时类平抛运动,则有:水平方向上:L=v0t,竖直方向上,
a=,联立解得:,而,所以:
v=.故C正确,A、B、D错误。
故选:C。
【点评】本题采取逆向思维,关键掌握求解类平抛运动的方法,类平抛运动在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动.
9.(4分)如图所示,在排球比赛中,假设排球运动员某次发球后排球恰好从网上边缘过网,排球网高H=2.24m,排球质量为m=300g,运动员对排球做的功为W1=20J,排球运动过程中克服空气阻力做功为W2=4.12J,重力加速度g=10m/s2.球从手刚发出位置的高度h=2.04m,选地面为零势能面,则( )
A.与排球从手刚发出相比较,排球恰好到达球网上边缘时重力势能的增加量为6.72 J
B.排球恰好到达球网上边缘时的机械能为22 J
C.排球恰好到达球网上边缘时的动能为15.88 J
D.与排球从手刚发出相比较,排球恰好到达球网上边缘时动能的减少量为4.72 J
【分析】重力势能的增加量由克服重力做功求解。根据功能原理求排球恰好到达球网上边缘时的机械能。由动能定理求排球恰好到达球网上边缘时的动能。与排球从手刚发出相比较,可求得排球恰好到达球网上边缘时动能的减少量。
【解答】解:A、与排球从手刚发出相比较,排球恰好到达球网上边缘时重力势能的增加量为 mg(H﹣h)=0.3×10×(2.24﹣2.04)=0.6 J,故A错误;
B、根据功能关系可得,排球恰好到达球网上边缘时的机械能为 mgh+W1﹣W2=0.3×10×2.04+20﹣4.12=22 J,故B正确;
C、由动能定理可知:排球恰好到达球网上边缘时的动能为 W1﹣W2﹣mg(H﹣h)=15.28 J,故C错误;
D、与排球从手刚发出相比较,排球恰好到达球网上边缘时动能的减少量为 W2+mg(H﹣h)=4.72 J,故D正确。
故选:BD。
【点评】本题考查了动能定理、重力势能的变化及功能关系的直接应用,关键要正确分析功与能的关系,判断能量是如何转化的。
10.(4分)如图所示为通过弹射器研究轻弹簧的弹性势能的实验装置.半径为R的光滑圆形轨道竖直固定于光滑水平面上并与水平地面相切于B点,弹射器固定于A处.某次实验过程中弹射器射出一质量为m的小球,恰能沿圆轨道内侧到达最髙点C,然后从轨道D处(D与圆心等高)下落至水平面.忽略空气阻力,取重力加速度为g.下列说法正确的是( )
A.小球从D处下落至水平面的时间小于
B.小球运动至最低点B时对轨道压力为5mg
C.小球落至水平面时的动能为2mgR
D.释放小球前弹射器的弹性势能为
【分析】小球从被弹出后机械能守恒;在最高点应保证重力充当向心力,由临界条件可求得最高点的速度;由机械能守恒可求得B点的压力、小球到达水平面的动能及开始时的机械能.
【解答】解:A、小球恰好通过最高点,则由mg=m,解得v=;小球从C到D的过程中机械能守恒,则有mgR=﹣mv2;解得vD=;小球由D到地面做匀加速直线运动;若做自由落体运动时,由R=可得,t=;而现在有初速度,故时间小于;故A正确;
B、由B到C过程中,机械能守恒,则有:mg2R=﹣;B点时由牛顿第二定律有:F﹣mg=m;联立解得,F=6mg,故B错误;
C、对C到地面过程由机械能守恒得:Ek﹣=mg2R;EK=2.5mgR;故C错误;
D、小球弹出后的机械能等于弹射器的弹性势能;故弹性势能为E=mg2R+=;故D正确;
故选:AD。
【点评】本题考查功能关系及机械能守恒定律,要注意明确系统只有重力及弹簧的弹力做功,故机械能守恒;正确选择初末状态即可顺利求解.
11.(4分)如图所示,有一范围足够大的水平匀强磁场,磁感应强度为B,一个质量为m,电荷量为+q的带电小圆环套在一根固定的绝缘竖直长杆上,环与杆间的动摩擦因数为μ,现使圆环以初速度v0向上运动,经时间t0圆环回到出发点,不计空气阻力,取竖直向上为正方向,下列描述该过程中圆环的速度v随时间t、摩擦力f随时间t、动能Et随位移x、机械能E随位移x变化规律的图象中,可能正确的是( )
A. B.
C. D.
【分析】小球受重力、洛伦兹力、支持力和滑动摩擦力,然后根据牛顿第二定律列式,推导出纵坐标与横坐标的关系式,由此进行解答.
【解答】解:小球向上运动的过程中受重力、洛伦兹力、支持力和向下的滑动摩擦力,向上运动,重力和摩擦力做负功,速度不断减小,洛伦兹力不断减小,支持力减小,故滑动摩擦力减小,合力减小,物体做加速度不断减小的加速运动,当速度减为零时,向上的位移最大,摩擦力等于0,而加速度等于重力加速度;
小球达到最高点后向下运动的过程中受重力、洛伦兹力、支持力和向上的滑动摩擦力,由于速度不断变大,洛伦兹力不断变大,支持力变大,故滑动摩擦力变大,合力减小,物体做加速度不断减小的加速运动,当加速度减为零时,速度最大;
A、由以上的分析可知,小球先向上运动,加速度逐渐减小;后小球向下运动,加速度仍然继续减小。负号表示速度的方向前后相反。故A正确;
B、由以上的分析可知,小球先向上运动,摩擦力的方向向下,逐渐减小;后小球向下运动,摩擦力的方向向上,逐渐增大。故B正确;
C、小球向上运动的过程中:Ek=Ek0﹣WG﹣Wf=Ek0﹣mgx﹣fx,由于f逐渐减小,所以动能的变化率逐渐减小。故C错误;
D、小球运动的过程中摩擦力做功使小球的机械能减小,向上运动的过程中:△E=﹣f△x,由于向上运动的过程中f逐渐减小,所以机械能的变化率逐渐减小;而向下运动的过程中摩擦力之间增大,所以机械能的变化率逐渐增大。故D正确。
故选:ABD。
【点评】本题关键分析清楚带电小球的运动情况,明确:向上运动的过程中摩擦力逐渐减小,向下运动的过程中摩擦力逐渐增大,加速度、速度和动能、机械能都随之发生 变化.
12.(4分)在光滑的足够长的斜面上横放一电阻可忽略不计的金属杆,如图所示,让金属杆从静止向下运动一段时间.已知此时间内重力做了W1的功,金属杆克服安培力做了W2的功,下列关于此过程的讲法正确的是( )
A.此过程中动能增加了(W1﹣W2)
B.此过程中机械能增加了(W1﹣W2)
C.此过程中重力势能减少了W1
D.此过程中回路中产生了W2的电能
【分析】动能的变化量等于外力所做的总功,由动能定理分析.机械能的变化等于除重力以外的力做功,由功能原理分析.重力势能的变化由重力做功分析.回路中产生的电能等于克服安培力做功.
【解答】解:A、由题知,安培力做功为﹣W2,由动能定理得:动能的增加量为△Ek=W1﹣W2.故A正确。
B、根据功能原理可知,机械能增加量为﹣W2.故B错误。
C、重力做了W1的功,则重力势能减少了W1.故C正确。
D、回路中产生的电能等于克服安培力做功。则此过程中回路中产生了W2的电能。故D正确。
故选:ACD。
【点评】本题从能量的角度研究电磁感应,关键要正确把握功与能的对应关系,明确回路中产生的电能等于克服安培力做功.
二.填空题:(2个小题,共12分)
13.(4分)“验证机械能守恒定律”的实验可以采用如图l所示的(甲)或(乙)方案来进行.
(1)比较这两种方案, 甲 (填“甲”或“乙”)方案好些,理由是 因为这个方案摩擦阻力小,误差小,操作方便,所用实验器材少 .
(2)如图2是采用(甲)方案时得到的一条纸带,在计算图中N点速度时,几位同学分别用下列不同的方法进行,其中正确的是 BC
A.vN=gnT
B.vN=
C.vN=
D.vN=g(n﹣1)T.
【分析】(1)解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项,能够根据实验装置和实验中需要测量的物理量进行选择;
(2)根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出某点的瞬时速度.
【解答】解:(1)机械能守恒的前提是只有重力做功,实际操作的方案中应该使摩擦力越小越好.故甲方案好一些.
(2)根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出某点的瞬时速度,可以求出N点的速度,据图上的数据可知:vN==,故AD错误,BC正确.
故答案为:(1)甲;因为这个方案摩擦阻力小,误差小,操作方便,所用实验器材少;(2)BC.
【点评】要从实验原理、实验仪器、实验步骤、实验数据处理、实验注意事项这几点去搞清楚,同时我们要加强物理基本规律在实验中的应用.
14.(8分)小明同学想测量一节旧干电池的电动势和内电阻,身边仅有下列器材:一个多用电表、一个定值电阻R1、一个滑动变阻器R2(0~20Ω)、一个开关S、导线若干.小明设计了实验原理图(如图甲所示),并进行了如下实验:
①根据原理图,连接实验器材,且S断开;
②多用电表选择“R×1”挡,先 欧姆调零 ,后用红表笔接a端,黑表笔接b端,记录下R1示数(如图乙所示);
③S闭合,多用电表选择“直流电压2.5V”挡, 红 表笔接a端, 黑 表笔接b端(选填“红”或“黑”),记录下示数U1;然后再测出b、c间的电压,记录下示数U2;
④调节滑动变阻器,重复步骤③,得到如下表所示的6组数据;
U1/V
0.10
0.20
0.30
0.40
0.50
0.60
U2/V
1.05
0.90
0.75
0.70
0.45
0.30
(1)请你完成上述操作步骤中的三处填空;
(2)由图乙可知R1测量值为 8 Ω;
(3)请在如图丙所示的坐标纸中画出U2﹣U1关系图;
(4)该电池的内电阻为 3.7 Ω.(保留两位有效数字)
【分析】(1)多用电表在测量电阻时每次换档都要进行欧姆调零;在用电压表测电压时,应保证红进黑出;
(2)欧姆档读数时读最上方刻度;注意要乘以倍率;
(3)由表格中数据利用描点法作出图象;
(4)由电路图及闭合电路欧姆定律列出关于两电压示数的表达式,再结合图象求出内电阻.
【解答】解:(1)选择档位后,应进行欧姆调零;在采用电压表测量时,电流应保证红进黑出,故红表笔接a端;黑表笔接b端;
(2)由指针示数可知,电阻为8×1=8Ω;
(3)采用描点法作出图象,如下图所示;
(4)由闭合电路欧姆定律可知,E=(U1+U2)+;
则有:U2=E﹣U1﹣;
由图可知,k==1.46=(1+)
解得:r=3.7Ω;
故答案为:(1)欧姆调零;a;b;(2)8;(3)如下图;(4)3.7
【点评】本题考查闭合电路欧姆定律及多用电表的使用方法,在解答时要注意分析题意,正确得出欧姆定律表达式,才能够应用数学规律求解.
三.计算题:(3个小题,共33分)
15.(9分)如图所示,在倾角为30°的光滑斜面上,一劲度系数为K=200N/m的轻质弹簧一端连接固定挡板C上,另一端连接一质量为m=4Kg的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端与质量也为m的物体B相连,细绳与斜面平行,斜面足够长,用手托住物体B使绳子刚好没有拉力,然后由静止释放,求:
(1)弹簧恢复原长时细绳上的拉力;
(2)物体A沿斜面向上运动多远时获得最大速度;
(3)物体A的最大速度大小.
【分析】(1)回复原长时,分别对A和B应用牛顿第二定律列式即可求解绳子的拉力,
(2、3)没有释放时,对于物体A由平衡条件求出此时弹簧的压缩量,释放后A沿斜面向上做加速度减小的加速运动,当A加速度为0时,A速度最大,对AB分别根据平衡条件求出此时弹簧的伸长量,进而判断在此过程中弹簧弹性势能改变量,设最大速度为υ,对于A、B及弹簧组成的系统由机械能守恒即可求出A的最大速度值;
【解答】解:(1)回复原长时,
对B:mg﹣T=ma
对A:T﹣mgsin30°=ma
代入数据解得:T=30N
(2)初始位置,弹簧的压缩量为:
,
当A速度最大时,有:mg=kx2+mgsin30°
弹簧的伸长量为:
所以A沿斜面上升的距离为:x=x1+x2=20cm
(3)因为x1=x2,所以弹簧的弹性势能没有改变,由系统机械能守恒得:
mg(x1+x2)﹣mg(x1+x2)sin30°=
解得:v=g
答:(1)弹簧恢复原长时细绳上的拉力为30N;
(2)物体A沿斜面向上运动20cm时获得最大速度;
(3)物体A的最大速度大小为1m/s.
【点评】本题解题的关键是根据两个物体的受力分析判断运动情况,知道当A加速度为0时,A速度最大,此时AB受力都平衡,运动过程中A、B及弹簧组成的系统机械能守恒,难度适中.
16.(12分)如图所示,在平面直角坐标系xoy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从电场中Q(﹣2h,﹣h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子从Q点运动到N点的时间t.
【分析】(1)带电粒子在电场中做类平抛运动,由类似平抛运动规律列方程求解E的大小;
(2)粒子在竖直方向做匀加速直线运动由速度时间公式求出vy,根据tanα=求正切值;由粒子进入磁场时的速度方向与射出磁场时的速度方向可确定圆心与半径,然后根据洛伦兹力提供向心力列方程求得B大小;
(3)粒子在电场中的运动时间等于水平分运动时间;粒子在磁场和电场之间的运动是匀速直线运动;粒子从Q点运动到N点是匀速圆周运动,圆心角为45°,根据t=求解磁场中的运动时间;最后求和得到总时间.
【解答】解:(1)粒子在电场中运动过程中,由平抛运动规律及牛顿运动定律得:
2h=v0t
h=at2
qE=ma
联立解得:
;
(2)粒子到达O点时,沿+y方向的分速度:
速度与x正方向的夹角α满足:
粒子从MP的中点垂直于MP进入磁场,垂直于NP射出磁场,粒子在磁场中的速度,轨道半径由,
解得:;
(3)粒子在电场中的运动时间:
粒子在磁场和电场之间的运动时间为:
=
粒子在磁场中的运动时间为:
故总时间为:
t=+;
答:(1)电场强度的大小E为;
(2)磁感应强度的大小B为;
(3)粒子聪Q点运动到N点的时间t为+.
【点评】带电粒子在电磁场中的运动要注意分析过程,并结合各过程中涉及到的运动规律采用合理的物理规律求解.
17.(12分)如图所示,两平行导轨间距L=0.1m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角θ=30°,垂直斜面方向向上磁感应强度B=0.5T,水平部分没有磁场。金属棒ab质量m=0.005kg,电阻r=0.02Ω,运动中与导轨有良好接触,并且垂直于导轨,电阻R=0.08Ω,其余电阻不计,当金属棒从斜面上离地高h=1.0m以上任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25m.(取g=10m/s2),求:
(1)棒在斜面上的最大速度?
(2)水平面的滑动摩擦因数?
(3)从高度h=1.0m处滑下后电阻R上产生的热量?
【分析】1、到达水平面之前已经开始匀速运动mgsinθ=F,F=BIL,根据闭合电路的欧姆定律,感应电流=,则可以联列解得最大速度v。
2、金属棒在水平面做匀减速运动,有v2=2ax,解出加速度a.金属棒在摩擦力作用下做匀减速运动f=ma,可解得摩擦力f.摩擦力f=μmg,可解得动摩擦因数。
3、下滑的过程中,由动能定理可得:,可解得安培力做的功,安培力所做的功等于电路中产生的焦耳热W=Q,又因为电阻R上产生的热量:,代入数据可得电阻R上产生的热量。
【解答】解:(1)到达水平面之前已经开始匀速运动,设最大速度为v,感应电动势为:
E=BLv
感应电流为:
安培力为:F=BIL
匀速运动时,沿斜面方向上受力有:mgsinθ=F
联立解得:v=1.0m/s
(2)在水平面上滑动时,滑动摩擦力为:f=μmg
金属棒在摩擦力作用下做匀减速运动,由牛顿第二定律有:f=ma
金属棒在水平面做匀减速运动,由运动学公式有:v2=2ax
联立解得:μ=0.04
(3)下滑的过程中,由动能定理可得:
安培力所做的功等于电路中产生的焦耳热,即为:W=Q
电阻R上产生的热量:
代入数据解得:QR=3.8×10﹣2 J。
答:(1)棒在斜面上的最大速度为1m/s。
(2)水平面的滑动摩擦因数为0.04。
(3)从高度h=1.0m处滑下后电阻R上产生的热量为3.8×10﹣2 J。
【点评】本题要注意用平衡条件解决磁场中导体的平衡问题,关键在于安培力的分析和计算,并不难。在匀强磁场中,当通电导体与磁场垂直时,安培力大小F=BIL,方向由左手定则判断。
选考题:共15分.请从给出的三道题中任选一题作答,如果多做,则按所做的第一题计分【选修3-3】(15分)
18.(5分)下列说法中正确的是( )
A.布朗运动并不是液体分子的运动,但它说明分子永不停息地做无规则运动
B.叶面上的小露珠呈球形是由于液体表面张力的作用
C.液晶显示器是利用了液晶对光具有各向异性的特点
D.当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小
【分析】依据布朗运动现象和实质判定A;
由表面张力的形成原因判定B;
液晶的特征是具有光学异性,故可以制作显示器;
依据分子力做功判定分析势能;
【解答】解:
A、布朗运动是悬浮在液体中的固体小颗粒的运动,它说明液体分子永不停息地做无规则运动。故A正确;
B、液体表面张力产生的原因是:液体跟气体接触的表面存在一个薄层,叫做表面层,表面层里的分子比液体内部稀疏,分子间的距离比液体内部大一些,分子间的相互作用表现为引力。露珠的形成就是由于液体表面张力的作用,故B正确;
C、液晶显示器是利用了液晶对光具有各向异性的特点,故C正确;
D、当两分子间距离大于平衡位置的间距r0时,分子力表现为引力,故随分子间的距离增大,分子力做负功,分子势能增大,故D错误;
故选:ABC。
【点评】该题关键是掌握布朗运动的现象和实质;其次要会分析分子力随距离的变化,以及分子力做功与分子势能变化关系,这些是重点考查内容。
19.(10分)如图所示,在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内,用4cm高的水银柱封闭着51cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg。
①若缓慢对玻璃管加热,当水银柱上表面与管口刚好相平时,求管中气体的温度;
②若保持管内温度始终为33℃,现将水银缓慢注入管中,直到水银柱上表面与管口相平,求此时管中气体的压强。
【分析】(1)对气体加热的过程中,气体的压强不变,求出气体的状态参量,然后根据玻意耳定律和盖﹣吕萨克定律求出气体的温度。
(2)当水银柱上表面与管口相平,设水银柱的高度为H,管内气体经等温压缩,由玻意耳定律即可求出结果。
【解答】解:①设玻璃管横截面积为S,以管内封闭气体为研究对象,气体经等压膨胀:
初状态:V1=51S,T1=306K;
末状态:V2=53S,T2=?
由盖吕萨克定律:
解得:T2=318K
②当水银柱上表面与管口相平,设此时管中气体压强为p,水银柱的高度为H,管内气体经等温压缩,
初状态:V1=51S,p1=80cmHg
末状态:V2=(57﹣H)S,p2=(76+H)cmHg
由玻意耳定律:p1V1=p2V2
得:H=9cm
故:p2=85cmHg
答:①若缓慢对玻璃管加热,当水银柱上表面与管口刚好相平时,管中气体的温度是318K;
②若保持管内温度始终为33℃,现将水银缓慢注入管中,直到水银柱上表面与管口相平,此时管中气体的压强是85cmHg。
【点评】本题考查了应用理想气体状态方程求气体压强,分析清楚气体状态变化过程是正确解题的关键。
【选修3-4】(15分)
20.A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图中甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图中丙、丁所示,则A、B两列波的波速vA、vB之比可能是( )
A.1:1 B.2:1 C.1:2 D.3:1
E.1:3
【分析】由题,甲、丙图象反相,t小于A波的周期TA,说明A波经过了半个周期.B波的图象与原来重合,说明经过了整数倍周期.由图读出两波的波长,由题分别得到周期与时间的关系,由波速公式得到波速的关系式,再进行选择.
【解答】解:由图读出,A波波长为λA=24cm,甲图到丙图一定是半个周期,所以周期TA=2t;B波波长为λB=12cm,乙图与丁图的波形图相同,经过的时间一定是整数个周期,所以周期TB=,波速vA=,vB=,
得到vA:vB=1:n,所以A、B两列波的波速vA、vB之比可能是ACE,不可能的是B、D。
故选:ACE。
【点评】本题中知道两个时刻波形图,抓住经过半个周期时间,波形反相;经过整数倍周期时间,图象重合是关键.
21.有一玻璃球冠,右侧面镀银,光源S就在其对称轴上,如图所示,从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折射入玻璃球冠内,经右侧镀银面第一次反射恰能沿原路返回,若球面半径为R,玻璃折射率为,求光源S与球冠顶点M之间的距离SM为多大?
【分析】作出光路图,根据折射定律和几何关系,求出入射角和折射角,再由几何关系求解光源S与球心O之间的距离SO,从而得到SM.
【解答】解:如图所示,根据折射定律,有:
n=
根据反射定律,有:θ1=θ3
其中:θ3+θ2=90°
联立可得:θ1=60°,θ2=30°
由图,有:β=θ2=30°,α=θ1﹣β=30°
故:SO=R
故光源S与M间距:SN=SO﹣R=(﹣1)R≈0.73R
答:光源S与球冠顶点M之间的距离SM为0.73R.
【点评】处理几何光学相关的问题,关键是作出光路图,一定要用直尺准确作图,然后根据几何图形的特点求角或者线段的长度.
【选修3-5】(15分)
22.以下说法符合物理学史的是 ( )
A.普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元
B.康普顿效应表明光子具有能量
C.德布罗意把光的波粒二象性推广到实物粒子,认为实物粒子也具有波动性
D.汤姆逊通过α粒子散射实验,提出了原子具有核式结构
E.卢瑟福利用α粒子轰击氮核发现了质子,并预言了中子的存在
【分析】根据物理学史和常识解答,记住著名物理学家的主要贡献即可。
【解答】解:A、普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元,故A正确;
B、康普顿效应不仅表明了光子具有能量,还表明了光子具有动量,故B错误;
C、德布罗意把光的波粒二象性推广到实物粒子,认为实物粒子也具有波动性,故C正确;
D、卢瑟福在用α粒子轰击金箔的实验中发现了质子,并预言了中子的存在,提出原子核式结构学说,故D错误,E正确;
故选:ACE。
【点评】本题考查物理学史,是常识性问题,对于物理学上重大发现、发明、著名理论要加强记忆,这也是考试内容之一。
23.如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连。另一质量为m的小物块A以速度v0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计。(所有过程都在弹簧弹性限度范围内)求:
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比。
【分析】(1)A、B发生弹性碰撞,碰撞过程动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出碰后两物体的速度。
(2)在B压缩弹簧过程中,系统机械能守恒,由机械能守恒定律可以求出弹簧的弹性势能;当弹簧第一次伸长最长时,B、C两物体组成的系统动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出弹簧的弹性势能,然后求出弹簧的弹性势能之比。
【解答】解:(1)A、B发生弹性正碰,碰撞过程中,A、B组成的系统动量守恒、机械能守恒,以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得:
mv0=mvA+2mvB,
在碰撞过程中机械能守恒,由机械能守恒定律得:
mv02=mvA2+?2mvB2,
联立解得:vA=﹣v0,vB=v0;
(2)弹簧第一次压缩到最短时,B的速度为零,该过程机械能守恒,由机械能守恒定律得,弹簧的弹性势能:
EP=?2m?vB2=mv02,
从弹簧压缩最短到弹簧恢复原长时,B、C与弹簧组成的系统机械能守恒,
弹簧恢复原长时,B的速度vB=v0,速度方向向右,C的速度为零,
从弹簧恢复原长到弹簧第一次伸长最长时,B、C与弹簧组成的系统动量守恒、机械能守恒,
弹簧伸长最长时,B、C速度相等,以向右为正方向,由动量守恒定律得:
2mvB=(2m+2m)v′,
由机械能守恒定律得:
?2m?vB2=?(2m+2m)?v′2+EP′,
解得:EP′=mv02,
弹簧第一次压缩最短与第一次伸长最长时弹性势能之比:EP:EP′=2:1;
答:(1)A、B碰后瞬间,A的速度为v0,方向向右,B的速度为v0,方向向左;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比为2:1。
【点评】本题考查了物体的速度与弹簧弹性势能之比,应用动量守恒定律与机械能守恒定律即可正确解题,分析清楚物体运动过程是正确 解题的关键。
一.选择题(本题共12题,共40分.其中第1-8题只有一个选项正确,每小题3分;第9-12有多个选项正确,每小题3分,全部选对得4分,选对但不全得2分,有选错得0分)
1.(3分)下列关于物理学史和物理研究方法的叙述中,正确的是( )
A.用点电荷来代替带电体的研究方法叫微元法
B.伽利略借助实验研究和逻辑推理得出了自由落体运动规律
C.利用v﹣t图象推导匀变速直线运动位移公式的方法是理想模型法
D.法拉第发现电流的磁效应与他坚信电和磁之间一定存在联系的哲学思想是分不开的
2.(3分)如图所示,在粗糙水平面上放置A、B、C、D四个小物块,各小物块之间由四根完全相同的轻弹簧相互连接,正好组成一个菱形,∠BAD=120°,整个系统保持静止状态.已知A物块所受的摩擦力大小为f,则D物块所受的摩擦力大小为( )
A.f B.f C.f D.2 f
3.(3分)质量为2kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.重力加速度g取10m/s2,则物体在t=0至t=12s这段时间的位移大小为( )
A.18 m B.54 m C.72 m D.198 m
4.(3分)如图所示,水平面上固定有一个斜面,从斜面顶端向右平抛一只小球,当初速度为v0时,小球恰好落到斜面底端,平抛的飞行时间为t0.现用不同的初速度v从该斜面顶端向右平抛这只小球,以下哪个图象能正确表示平抛的飞行时间t随v变化的函数关系( )
A. B.
C. D.
5.(3分)如图所示,内壁光滑的半球形碗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则( )
A.球A的角速度小于球B的角速度
B.球A的线速度小于球B的线速度
C.球A对碗壁的压力等于球B对碗壁的压力
D.球A的向心加速度大于球B的向心加速度
6.(3分)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的平均密度ρ=
C.月球的第一宇宙速度v=
D.月球的质量m月=
7.(3分)两个等量异种点电荷位于x轴上,相对原点对称分布,正确描述电势φ随位置x变化规律的是图( )
A. B.
C. D.
8.(3分)如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速度、质量为m的电子.若极板长为L,间距为d,当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离两板等距.已知元电荷为e,则从放射源O发射出的电子的这一速度为( )
A. B.
C. D.
9.(4分)如图所示,在排球比赛中,假设排球运动员某次发球后排球恰好从网上边缘过网,排球网高H=2.24m,排球质量为m=300g,运动员对排球做的功为W1=20J,排球运动过程中克服空气阻力做功为W2=4.12J,重力加速度g=10m/s2.球从手刚发出位置的高度h=2.04m,选地面为零势能面,则( )
A.与排球从手刚发出相比较,排球恰好到达球网上边缘时重力势能的增加量为6.72 J
B.排球恰好到达球网上边缘时的机械能为22 J
C.排球恰好到达球网上边缘时的动能为15.88 J
D.与排球从手刚发出相比较,排球恰好到达球网上边缘时动能的减少量为4.72 J
10.(4分)如图所示为通过弹射器研究轻弹簧的弹性势能的实验装置.半径为R的光滑圆形轨道竖直固定于光滑水平面上并与水平地面相切于B点,弹射器固定于A处.某次实验过程中弹射器射出一质量为m的小球,恰能沿圆轨道内侧到达最髙点C,然后从轨道D处(D与圆心等高)下落至水平面.忽略空气阻力,取重力加速度为g.下列说法正确的是( )
A.小球从D处下落至水平面的时间小于
B.小球运动至最低点B时对轨道压力为5mg
C.小球落至水平面时的动能为2mgR
D.释放小球前弹射器的弹性势能为
11.(4分)如图所示,有一范围足够大的水平匀强磁场,磁感应强度为B,一个质量为m,电荷量为+q的带电小圆环套在一根固定的绝缘竖直长杆上,环与杆间的动摩擦因数为μ,现使圆环以初速度v0向上运动,经时间t0圆环回到出发点,不计空气阻力,取竖直向上为正方向,下列描述该过程中圆环的速度v随时间t、摩擦力f随时间t、动能Et随位移x、机械能E随位移x变化规律的图象中,可能正确的是( )
A. B.
C. D.
12.(4分)在光滑的足够长的斜面上横放一电阻可忽略不计的金属杆,如图所示,让金属杆从静止向下运动一段时间.已知此时间内重力做了W1的功,金属杆克服安培力做了W2的功,下列关于此过程的讲法正确的是( )
A.此过程中动能增加了(W1﹣W2)
B.此过程中机械能增加了(W1﹣W2)
C.此过程中重力势能减少了W1
D.此过程中回路中产生了W2的电能
二.填空题:(2个小题,共12分)
13.(4分)“验证机械能守恒定律”的实验可以采用如图l所示的(甲)或(乙)方案来进行.
(1)比较这两种方案, (填“甲”或“乙”)方案好些,理由是 .
(2)如图2是采用(甲)方案时得到的一条纸带,在计算图中N点速度时,几位同学分别用下列不同的方法进行,其中正确的是
A.vN=gnT
B.vN=
C.vN=
D.vN=g(n﹣1)T.
14.(8分)小明同学想测量一节旧干电池的电动势和内电阻,身边仅有下列器材:一个多用电表、一个定值电阻R1、一个滑动变阻器R2(0~20Ω)、一个开关S、导线若干.小明设计了实验原理图(如图甲所示),并进行了如下实验:
①根据原理图,连接实验器材,且S断开;
②多用电表选择“R×1”挡,先 ,后用红表笔接a端,黑表笔接b端,记录下R1示数(如图乙所示);
③S闭合,多用电表选择“直流电压2.5V”挡, 表笔接a端, 表笔接b端(选填“红”或“黑”),记录下示数U1;然后再测出b、c间的电压,记录下示数U2;
④调节滑动变阻器,重复步骤③,得到如下表所示的6组数据;
U1/V
0.10
0.20
0.30
0.40
0.50
0.60
U2/V
1.05
0.90
0.75
0.70
0.45
0.30
(1)请你完成上述操作步骤中的三处填空;
(2)由图乙可知R1测量值为 Ω;
(3)请在如图丙所示的坐标纸中画出U2﹣U1关系图;
(4)该电池的内电阻为 Ω.(保留两位有效数字)
三.计算题:(3个小题,共33分)
15.(9分)如图所示,在倾角为30°的光滑斜面上,一劲度系数为K=200N/m的轻质弹簧一端连接固定挡板C上,另一端连接一质量为m=4Kg的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端与质量也为m的物体B相连,细绳与斜面平行,斜面足够长,用手托住物体B使绳子刚好没有拉力,然后由静止释放,求:
(1)弹簧恢复原长时细绳上的拉力;
(2)物体A沿斜面向上运动多远时获得最大速度;
(3)物体A的最大速度大小.
16.(12分)如图所示,在平面直角坐标系xoy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从电场中Q(﹣2h,﹣h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子从Q点运动到N点的时间t.
17.(12分)如图所示,两平行导轨间距L=0.1m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角θ=30°,垂直斜面方向向上磁感应强度B=0.5T,水平部分没有磁场。金属棒ab质量m=0.005kg,电阻r=0.02Ω,运动中与导轨有良好接触,并且垂直于导轨,电阻R=0.08Ω,其余电阻不计,当金属棒从斜面上离地高h=1.0m以上任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25m.(取g=10m/s2),求:
(1)棒在斜面上的最大速度?
(2)水平面的滑动摩擦因数?
(3)从高度h=1.0m处滑下后电阻R上产生的热量?
选考题:共15分.请从给出的三道题中任选一题作答,如果多做,则按所做的第一题计分【选修3-3】(15分)
18.(5分)下列说法中正确的是( )
A.布朗运动并不是液体分子的运动,但它说明分子永不停息地做无规则运动
B.叶面上的小露珠呈球形是由于液体表面张力的作用
C.液晶显示器是利用了液晶对光具有各向异性的特点
D.当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小
19.(10分)如图所示,在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内,用4cm高的水银柱封闭着51cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg。
①若缓慢对玻璃管加热,当水银柱上表面与管口刚好相平时,求管中气体的温度;
②若保持管内温度始终为33℃,现将水银缓慢注入管中,直到水银柱上表面与管口相平,求此时管中气体的压强。
【选修3-4】(15分)
20.A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图中甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图中丙、丁所示,则A、B两列波的波速vA、vB之比可能是( )
A.1:1 B.2:1 C.1:2 D.3:1
E.1:3
21.有一玻璃球冠,右侧面镀银,光源S就在其对称轴上,如图所示,从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折射入玻璃球冠内,经右侧镀银面第一次反射恰能沿原路返回,若球面半径为R,玻璃折射率为,求光源S与球冠顶点M之间的距离SM为多大?
【选修3-5】(15分)
22.以下说法符合物理学史的是 ( )
A.普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元
B.康普顿效应表明光子具有能量
C.德布罗意把光的波粒二象性推广到实物粒子,认为实物粒子也具有波动性
D.汤姆逊通过α粒子散射实验,提出了原子具有核式结构
E.卢瑟福利用α粒子轰击氮核发现了质子,并预言了中子的存在
23.如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连。另一质量为m的小物块A以速度v0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计。(所有过程都在弹簧弹性限度范围内)求:
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比。
2018-2019学年辽宁省朝阳市凌源二中高三(上)期末物理试卷
参考答案与试题解析
一.选择题(本题共12题,共40分.其中第1-8题只有一个选项正确,每小题3分;第9-12有多个选项正确,每小题3分,全部选对得4分,选对但不全得2分,有选错得0分)
1.(3分)下列关于物理学史和物理研究方法的叙述中,正确的是( )
A.用点电荷来代替带电体的研究方法叫微元法
B.伽利略借助实验研究和逻辑推理得出了自由落体运动规律
C.利用v﹣t图象推导匀变速直线运动位移公式的方法是理想模型法
D.法拉第发现电流的磁效应与他坚信电和磁之间一定存在联系的哲学思想是分不开的
【分析】物理学中对于多因素(多变量)的问题,常常采用控制因素(变量)的方法,把多因素的问题变成多个单因素的问题;每一次只改变其中的某一个因素,而控制其余几个因素不变,从而研究被改变的这个因素对事物影响,分别加以研究,最后再综合解决,这种方法叫控制变量法;它是科学探究中的重要思想方法,控制变量法是初中物理中常用的探索问题和分析解决问题的科学方法之一.
等效替代法是指在研究某一个物理现象和规律中,因实验本身的特殊限制或因实验器材等限制,不可以或很难直接揭示物理本质,而采取与之相似或有共同特征的等效现象来替代的方法.
【解答】解:A、用质点代替实际物体是采用了理想模型的方法,质点实际不存在,故A错误;
B、伽利略在研究自由落体运动时采用了推理的方法,故B正确;
C、在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法,故C错误;
D、法拉第发现电磁感应现象,和他坚信电与磁之间一定存在着联系的哲学思想分不开,故D错误;
故选:B。
【点评】解决此题要知道常用的物理学研究方法:控制变量法、等效替代法、模型法、比较法、分类法、类比法、转换法等.
2.(3分)如图所示,在粗糙水平面上放置A、B、C、D四个小物块,各小物块之间由四根完全相同的轻弹簧相互连接,正好组成一个菱形,∠BAD=120°,整个系统保持静止状态.已知A物块所受的摩擦力大小为f,则D物块所受的摩擦力大小为( )
A.f B.f C.f D.2 f
【分析】物体在水平面上受弹簧弹力和静摩擦力平衡,根据力的合成方法求解弹簧的弹力.
【解答】解:已知A物块所受的摩擦力大小为f,设每根弹簧的弹力为F,则有:2Fcos60°=f,对D:2Fcos30°=f′,解得:f′=F=f
故选:C。
【点评】本题考查了物体受共点力平衡和力的合成计算,难度不大.
3.(3分)质量为2kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等.从t=0时刻开始,物体受到方向不变、大小呈周期性变化的水平拉力F的作用,F随时间t的变化规律如图所示.重力加速度g取10m/s2,则物体在t=0至t=12s这段时间的位移大小为( )
A.18 m B.54 m C.72 m D.198 m
【分析】本题的关键是根据F﹣t图象分别对不同的时间段进行分析,注意0到3s时间内,由于物体受到的合力恰好为零,所以物体仍保持静止;第二段时间内,物体做匀加速直线运动,可根据牛顿运动定律求出位移;第三段时间内,物体做匀速直线运动,第四段时间内,物体做匀加速直线运动,根据运动学公式分别求出各段时间内的位移,然后相加即可.
【解答】解:对物体受力分析可知,0到3s内,由于滑动摩擦力为:==0.2×20N=4N,恰好等于外力F大小,所以物体仍能保持静止状态,
3到6s内,物体产生的加速度为:a==,发生的位移为:===9m
6到9s内,物体所受的合力为零,做匀速直线运动,由于6s时的速度为:v=at=2×3=6m/s,所以发生的位移为:=vt=6×(9﹣6)=18m
9到12s内,物体做匀加速直线运动,发生的位移为:=vt=6×3+=27m
所以总位移为:x=0=9+18+27=54m,所以B正确;
故选:B。
【点评】遇到多过程的动力学问题,应分别进行受力分析和运动过程分析,然后选取相应的物理规律进行求解,也可以借助v﹣t图象求解.
4.(3分)如图所示,水平面上固定有一个斜面,从斜面顶端向右平抛一只小球,当初速度为v0时,小球恰好落到斜面底端,平抛的飞行时间为t0.现用不同的初速度v从该斜面顶端向右平抛这只小球,以下哪个图象能正确表示平抛的飞行时间t随v变化的函数关系( )
A. B.
C. D.
【分析】根据小球落在斜面上,结合竖直位移与水平位移的关系求出运动的时间.小球落在地面上,高度一定,则运动时间一定.
【解答】解:当小球落在斜面上时,有:tanθ=,解得t=,与速度v成正比。
当小球落在地面上,根据h=得,t=,知运动时间不变。可知t与v的关系图线先是过原点的一条倾斜直线,然后是平行于横轴的直线。故C正确,A、B、D错误。
故选:C。
【点评】解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.
5.(3分)如图所示,内壁光滑的半球形碗固定不动,其轴线垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则( )
A.球A的角速度小于球B的角速度
B.球A的线速度小于球B的线速度
C.球A对碗壁的压力等于球B对碗壁的压力
D.球A的向心加速度大于球B的向心加速度
【分析】球受重力和支持力,靠重力和支持力的合力提供圆周运动的向心力,根据F合=ma=═mrω2,比较线速度、角速度和向心加速度的大小.并比较支持力的大小,从而能比较压力的大小.
【解答】解:ABD、对于任意一球,设其轨道处半球形碗的半径与竖直方向的夹角为θ,半球形碗的半径为R.根据重力和支持力的合力提供圆周运动的向心力,得:
F合=mgtanθ=ma==mrω2
又 r=Rsinθ
联立得:v=,a=gtanθ,
R一定,可知θ越大,线速度v越大、角速度ω越大、向心加速度a越大,所以球A的线速度大于球B的线速度,球A的角速度大于球B的角速度,球A的向心加速度大于球B的向心加速度。故AB错误,D正确。
C、受力分析可知:球所受的支持力FN=,θ越大,FN越大,则碗对A球的支持力较大,由牛顿第三定律知球A对碗壁的压力大于球B对碗壁的压力,C错误。
故选:D。
【点评】解决本题的关键知道小球做匀速圆周运动,靠重力和支持力的合力提供向心力,能灵活选择向心力的公式,由牛顿运动定律列式分析.
6.(3分)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的平均密度ρ=
C.月球的第一宇宙速度v=
D.月球的质量m月=
【分析】宇航员在月球上自高h处以初速度v0水平抛出一物体,测出物体的水平射程为L,根据水平射程和初速度求出运动的时间,
根据h=gt2求出月球表面的重力加速度大小;由g=求得月球的质量;根据重力提供向心力求出卫星的第一宇宙速度;由质量与半径可求得平均密度。
【解答】解:A、平抛运动的时间t=.再根据h=gt2,得g月=,故A错误;
B、由g月= 与g月=,可得:m月=,因此月球的平均密度ρ==.故B正确。
C、第一宇宙速度:v===,故C错误;
D、由g月= 与g月=,可得:m月=,故D错误;
故选:B。
【点评】解决本题的关键知道平抛运动在水平方向上和竖直方向上的运动规律,以及掌握万有引力提供向心力以及万有引力等于重力这两个理论的运用。
7.(3分)两个等量异种点电荷位于x轴上,相对原点对称分布,正确描述电势φ随位置x变化规律的是图( )
A. B.
C. D.
【分析】本题根据电场线的性质,沿电场线的方向电势降低进行判断即可。
【解答】解:两个等量异号电荷的电场线如下图,
根据“沿电场线方向电势降低”的原理,从左侧无穷远处向右电势应升高,正电荷所在位置处最高;然后再慢慢减小,O点处电势为零,则O点右侧电势为负,同理到达负电荷时电势最小,经过负电荷后,电势开始升高,直到无穷远处,电势为零;故B、C、D是错误的;A正确。
故选:A。
【点评】本题中应明确沿电场线的方向电势降低;并且异号电荷连线的中垂线上的电势为零;因为其中垂线为等势面,与无穷远处电势相等。
8.(3分)如图所示,一种射线管由平行金属板A、B和平行于金属板的细管C组成.放射源O在A极板左端,可以向各个方向发射不同速度、质量为m的电子.若极板长为L,间距为d,当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,细管C离两板等距.已知元电荷为e,则从放射源O发射出的电子的这一速度为( )
A. B.
C. D.
【分析】当A、B板加上电压U时,只有某一速度的电子能从细管C水平射出,逆过来看,该粒子做类平抛运动,通过类平抛运动求出粒子的末速度,即为放射源O发射出的电子的速度.
【解答】解:将从细管C水平射出的电子逆过来看,时类平抛运动,则有:水平方向上:L=v0t,竖直方向上,
a=,联立解得:,而,所以:
v=.故C正确,A、B、D错误。
故选:C。
【点评】本题采取逆向思维,关键掌握求解类平抛运动的方法,类平抛运动在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动.
9.(4分)如图所示,在排球比赛中,假设排球运动员某次发球后排球恰好从网上边缘过网,排球网高H=2.24m,排球质量为m=300g,运动员对排球做的功为W1=20J,排球运动过程中克服空气阻力做功为W2=4.12J,重力加速度g=10m/s2.球从手刚发出位置的高度h=2.04m,选地面为零势能面,则( )
A.与排球从手刚发出相比较,排球恰好到达球网上边缘时重力势能的增加量为6.72 J
B.排球恰好到达球网上边缘时的机械能为22 J
C.排球恰好到达球网上边缘时的动能为15.88 J
D.与排球从手刚发出相比较,排球恰好到达球网上边缘时动能的减少量为4.72 J
【分析】重力势能的增加量由克服重力做功求解。根据功能原理求排球恰好到达球网上边缘时的机械能。由动能定理求排球恰好到达球网上边缘时的动能。与排球从手刚发出相比较,可求得排球恰好到达球网上边缘时动能的减少量。
【解答】解:A、与排球从手刚发出相比较,排球恰好到达球网上边缘时重力势能的增加量为 mg(H﹣h)=0.3×10×(2.24﹣2.04)=0.6 J,故A错误;
B、根据功能关系可得,排球恰好到达球网上边缘时的机械能为 mgh+W1﹣W2=0.3×10×2.04+20﹣4.12=22 J,故B正确;
C、由动能定理可知:排球恰好到达球网上边缘时的动能为 W1﹣W2﹣mg(H﹣h)=15.28 J,故C错误;
D、与排球从手刚发出相比较,排球恰好到达球网上边缘时动能的减少量为 W2+mg(H﹣h)=4.72 J,故D正确。
故选:BD。
【点评】本题考查了动能定理、重力势能的变化及功能关系的直接应用,关键要正确分析功与能的关系,判断能量是如何转化的。
10.(4分)如图所示为通过弹射器研究轻弹簧的弹性势能的实验装置.半径为R的光滑圆形轨道竖直固定于光滑水平面上并与水平地面相切于B点,弹射器固定于A处.某次实验过程中弹射器射出一质量为m的小球,恰能沿圆轨道内侧到达最髙点C,然后从轨道D处(D与圆心等高)下落至水平面.忽略空气阻力,取重力加速度为g.下列说法正确的是( )
A.小球从D处下落至水平面的时间小于
B.小球运动至最低点B时对轨道压力为5mg
C.小球落至水平面时的动能为2mgR
D.释放小球前弹射器的弹性势能为
【分析】小球从被弹出后机械能守恒;在最高点应保证重力充当向心力,由临界条件可求得最高点的速度;由机械能守恒可求得B点的压力、小球到达水平面的动能及开始时的机械能.
【解答】解:A、小球恰好通过最高点,则由mg=m,解得v=;小球从C到D的过程中机械能守恒,则有mgR=﹣mv2;解得vD=;小球由D到地面做匀加速直线运动;若做自由落体运动时,由R=可得,t=;而现在有初速度,故时间小于;故A正确;
B、由B到C过程中,机械能守恒,则有:mg2R=﹣;B点时由牛顿第二定律有:F﹣mg=m;联立解得,F=6mg,故B错误;
C、对C到地面过程由机械能守恒得:Ek﹣=mg2R;EK=2.5mgR;故C错误;
D、小球弹出后的机械能等于弹射器的弹性势能;故弹性势能为E=mg2R+=;故D正确;
故选:AD。
【点评】本题考查功能关系及机械能守恒定律,要注意明确系统只有重力及弹簧的弹力做功,故机械能守恒;正确选择初末状态即可顺利求解.
11.(4分)如图所示,有一范围足够大的水平匀强磁场,磁感应强度为B,一个质量为m,电荷量为+q的带电小圆环套在一根固定的绝缘竖直长杆上,环与杆间的动摩擦因数为μ,现使圆环以初速度v0向上运动,经时间t0圆环回到出发点,不计空气阻力,取竖直向上为正方向,下列描述该过程中圆环的速度v随时间t、摩擦力f随时间t、动能Et随位移x、机械能E随位移x变化规律的图象中,可能正确的是( )
A. B.
C. D.
【分析】小球受重力、洛伦兹力、支持力和滑动摩擦力,然后根据牛顿第二定律列式,推导出纵坐标与横坐标的关系式,由此进行解答.
【解答】解:小球向上运动的过程中受重力、洛伦兹力、支持力和向下的滑动摩擦力,向上运动,重力和摩擦力做负功,速度不断减小,洛伦兹力不断减小,支持力减小,故滑动摩擦力减小,合力减小,物体做加速度不断减小的加速运动,当速度减为零时,向上的位移最大,摩擦力等于0,而加速度等于重力加速度;
小球达到最高点后向下运动的过程中受重力、洛伦兹力、支持力和向上的滑动摩擦力,由于速度不断变大,洛伦兹力不断变大,支持力变大,故滑动摩擦力变大,合力减小,物体做加速度不断减小的加速运动,当加速度减为零时,速度最大;
A、由以上的分析可知,小球先向上运动,加速度逐渐减小;后小球向下运动,加速度仍然继续减小。负号表示速度的方向前后相反。故A正确;
B、由以上的分析可知,小球先向上运动,摩擦力的方向向下,逐渐减小;后小球向下运动,摩擦力的方向向上,逐渐增大。故B正确;
C、小球向上运动的过程中:Ek=Ek0﹣WG﹣Wf=Ek0﹣mgx﹣fx,由于f逐渐减小,所以动能的变化率逐渐减小。故C错误;
D、小球运动的过程中摩擦力做功使小球的机械能减小,向上运动的过程中:△E=﹣f△x,由于向上运动的过程中f逐渐减小,所以机械能的变化率逐渐减小;而向下运动的过程中摩擦力之间增大,所以机械能的变化率逐渐增大。故D正确。
故选:ABD。
【点评】本题关键分析清楚带电小球的运动情况,明确:向上运动的过程中摩擦力逐渐减小,向下运动的过程中摩擦力逐渐增大,加速度、速度和动能、机械能都随之发生 变化.
12.(4分)在光滑的足够长的斜面上横放一电阻可忽略不计的金属杆,如图所示,让金属杆从静止向下运动一段时间.已知此时间内重力做了W1的功,金属杆克服安培力做了W2的功,下列关于此过程的讲法正确的是( )
A.此过程中动能增加了(W1﹣W2)
B.此过程中机械能增加了(W1﹣W2)
C.此过程中重力势能减少了W1
D.此过程中回路中产生了W2的电能
【分析】动能的变化量等于外力所做的总功,由动能定理分析.机械能的变化等于除重力以外的力做功,由功能原理分析.重力势能的变化由重力做功分析.回路中产生的电能等于克服安培力做功.
【解答】解:A、由题知,安培力做功为﹣W2,由动能定理得:动能的增加量为△Ek=W1﹣W2.故A正确。
B、根据功能原理可知,机械能增加量为﹣W2.故B错误。
C、重力做了W1的功,则重力势能减少了W1.故C正确。
D、回路中产生的电能等于克服安培力做功。则此过程中回路中产生了W2的电能。故D正确。
故选:ACD。
【点评】本题从能量的角度研究电磁感应,关键要正确把握功与能的对应关系,明确回路中产生的电能等于克服安培力做功.
二.填空题:(2个小题,共12分)
13.(4分)“验证机械能守恒定律”的实验可以采用如图l所示的(甲)或(乙)方案来进行.
(1)比较这两种方案, 甲 (填“甲”或“乙”)方案好些,理由是 因为这个方案摩擦阻力小,误差小,操作方便,所用实验器材少 .
(2)如图2是采用(甲)方案时得到的一条纸带,在计算图中N点速度时,几位同学分别用下列不同的方法进行,其中正确的是 BC
A.vN=gnT
B.vN=
C.vN=
D.vN=g(n﹣1)T.
【分析】(1)解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项,能够根据实验装置和实验中需要测量的物理量进行选择;
(2)根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出某点的瞬时速度.
【解答】解:(1)机械能守恒的前提是只有重力做功,实际操作的方案中应该使摩擦力越小越好.故甲方案好一些.
(2)根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出某点的瞬时速度,可以求出N点的速度,据图上的数据可知:vN==,故AD错误,BC正确.
故答案为:(1)甲;因为这个方案摩擦阻力小,误差小,操作方便,所用实验器材少;(2)BC.
【点评】要从实验原理、实验仪器、实验步骤、实验数据处理、实验注意事项这几点去搞清楚,同时我们要加强物理基本规律在实验中的应用.
14.(8分)小明同学想测量一节旧干电池的电动势和内电阻,身边仅有下列器材:一个多用电表、一个定值电阻R1、一个滑动变阻器R2(0~20Ω)、一个开关S、导线若干.小明设计了实验原理图(如图甲所示),并进行了如下实验:
①根据原理图,连接实验器材,且S断开;
②多用电表选择“R×1”挡,先 欧姆调零 ,后用红表笔接a端,黑表笔接b端,记录下R1示数(如图乙所示);
③S闭合,多用电表选择“直流电压2.5V”挡, 红 表笔接a端, 黑 表笔接b端(选填“红”或“黑”),记录下示数U1;然后再测出b、c间的电压,记录下示数U2;
④调节滑动变阻器,重复步骤③,得到如下表所示的6组数据;
U1/V
0.10
0.20
0.30
0.40
0.50
0.60
U2/V
1.05
0.90
0.75
0.70
0.45
0.30
(1)请你完成上述操作步骤中的三处填空;
(2)由图乙可知R1测量值为 8 Ω;
(3)请在如图丙所示的坐标纸中画出U2﹣U1关系图;
(4)该电池的内电阻为 3.7 Ω.(保留两位有效数字)
【分析】(1)多用电表在测量电阻时每次换档都要进行欧姆调零;在用电压表测电压时,应保证红进黑出;
(2)欧姆档读数时读最上方刻度;注意要乘以倍率;
(3)由表格中数据利用描点法作出图象;
(4)由电路图及闭合电路欧姆定律列出关于两电压示数的表达式,再结合图象求出内电阻.
【解答】解:(1)选择档位后,应进行欧姆调零;在采用电压表测量时,电流应保证红进黑出,故红表笔接a端;黑表笔接b端;
(2)由指针示数可知,电阻为8×1=8Ω;
(3)采用描点法作出图象,如下图所示;
(4)由闭合电路欧姆定律可知,E=(U1+U2)+;
则有:U2=E﹣U1﹣;
由图可知,k==1.46=(1+)
解得:r=3.7Ω;
故答案为:(1)欧姆调零;a;b;(2)8;(3)如下图;(4)3.7
【点评】本题考查闭合电路欧姆定律及多用电表的使用方法,在解答时要注意分析题意,正确得出欧姆定律表达式,才能够应用数学规律求解.
三.计算题:(3个小题,共33分)
15.(9分)如图所示,在倾角为30°的光滑斜面上,一劲度系数为K=200N/m的轻质弹簧一端连接固定挡板C上,另一端连接一质量为m=4Kg的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端与质量也为m的物体B相连,细绳与斜面平行,斜面足够长,用手托住物体B使绳子刚好没有拉力,然后由静止释放,求:
(1)弹簧恢复原长时细绳上的拉力;
(2)物体A沿斜面向上运动多远时获得最大速度;
(3)物体A的最大速度大小.
【分析】(1)回复原长时,分别对A和B应用牛顿第二定律列式即可求解绳子的拉力,
(2、3)没有释放时,对于物体A由平衡条件求出此时弹簧的压缩量,释放后A沿斜面向上做加速度减小的加速运动,当A加速度为0时,A速度最大,对AB分别根据平衡条件求出此时弹簧的伸长量,进而判断在此过程中弹簧弹性势能改变量,设最大速度为υ,对于A、B及弹簧组成的系统由机械能守恒即可求出A的最大速度值;
【解答】解:(1)回复原长时,
对B:mg﹣T=ma
对A:T﹣mgsin30°=ma
代入数据解得:T=30N
(2)初始位置,弹簧的压缩量为:
,
当A速度最大时,有:mg=kx2+mgsin30°
弹簧的伸长量为:
所以A沿斜面上升的距离为:x=x1+x2=20cm
(3)因为x1=x2,所以弹簧的弹性势能没有改变,由系统机械能守恒得:
mg(x1+x2)﹣mg(x1+x2)sin30°=
解得:v=g
答:(1)弹簧恢复原长时细绳上的拉力为30N;
(2)物体A沿斜面向上运动20cm时获得最大速度;
(3)物体A的最大速度大小为1m/s.
【点评】本题解题的关键是根据两个物体的受力分析判断运动情况,知道当A加速度为0时,A速度最大,此时AB受力都平衡,运动过程中A、B及弹簧组成的系统机械能守恒,难度适中.
16.(12分)如图所示,在平面直角坐标系xoy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从电场中Q(﹣2h,﹣h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子从Q点运动到N点的时间t.
【分析】(1)带电粒子在电场中做类平抛运动,由类似平抛运动规律列方程求解E的大小;
(2)粒子在竖直方向做匀加速直线运动由速度时间公式求出vy,根据tanα=求正切值;由粒子进入磁场时的速度方向与射出磁场时的速度方向可确定圆心与半径,然后根据洛伦兹力提供向心力列方程求得B大小;
(3)粒子在电场中的运动时间等于水平分运动时间;粒子在磁场和电场之间的运动是匀速直线运动;粒子从Q点运动到N点是匀速圆周运动,圆心角为45°,根据t=求解磁场中的运动时间;最后求和得到总时间.
【解答】解:(1)粒子在电场中运动过程中,由平抛运动规律及牛顿运动定律得:
2h=v0t
h=at2
qE=ma
联立解得:
;
(2)粒子到达O点时,沿+y方向的分速度:
速度与x正方向的夹角α满足:
粒子从MP的中点垂直于MP进入磁场,垂直于NP射出磁场,粒子在磁场中的速度,轨道半径由,
解得:;
(3)粒子在电场中的运动时间:
粒子在磁场和电场之间的运动时间为:
=
粒子在磁场中的运动时间为:
故总时间为:
t=+;
答:(1)电场强度的大小E为;
(2)磁感应强度的大小B为;
(3)粒子聪Q点运动到N点的时间t为+.
【点评】带电粒子在电磁场中的运动要注意分析过程,并结合各过程中涉及到的运动规律采用合理的物理规律求解.
17.(12分)如图所示,两平行导轨间距L=0.1m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接,倾斜部分与水平面的夹角θ=30°,垂直斜面方向向上磁感应强度B=0.5T,水平部分没有磁场。金属棒ab质量m=0.005kg,电阻r=0.02Ω,运动中与导轨有良好接触,并且垂直于导轨,电阻R=0.08Ω,其余电阻不计,当金属棒从斜面上离地高h=1.0m以上任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25m.(取g=10m/s2),求:
(1)棒在斜面上的最大速度?
(2)水平面的滑动摩擦因数?
(3)从高度h=1.0m处滑下后电阻R上产生的热量?
【分析】1、到达水平面之前已经开始匀速运动mgsinθ=F,F=BIL,根据闭合电路的欧姆定律,感应电流=,则可以联列解得最大速度v。
2、金属棒在水平面做匀减速运动,有v2=2ax,解出加速度a.金属棒在摩擦力作用下做匀减速运动f=ma,可解得摩擦力f.摩擦力f=μmg,可解得动摩擦因数。
3、下滑的过程中,由动能定理可得:,可解得安培力做的功,安培力所做的功等于电路中产生的焦耳热W=Q,又因为电阻R上产生的热量:,代入数据可得电阻R上产生的热量。
【解答】解:(1)到达水平面之前已经开始匀速运动,设最大速度为v,感应电动势为:
E=BLv
感应电流为:
安培力为:F=BIL
匀速运动时,沿斜面方向上受力有:mgsinθ=F
联立解得:v=1.0m/s
(2)在水平面上滑动时,滑动摩擦力为:f=μmg
金属棒在摩擦力作用下做匀减速运动,由牛顿第二定律有:f=ma
金属棒在水平面做匀减速运动,由运动学公式有:v2=2ax
联立解得:μ=0.04
(3)下滑的过程中,由动能定理可得:
安培力所做的功等于电路中产生的焦耳热,即为:W=Q
电阻R上产生的热量:
代入数据解得:QR=3.8×10﹣2 J。
答:(1)棒在斜面上的最大速度为1m/s。
(2)水平面的滑动摩擦因数为0.04。
(3)从高度h=1.0m处滑下后电阻R上产生的热量为3.8×10﹣2 J。
【点评】本题要注意用平衡条件解决磁场中导体的平衡问题,关键在于安培力的分析和计算,并不难。在匀强磁场中,当通电导体与磁场垂直时,安培力大小F=BIL,方向由左手定则判断。
选考题:共15分.请从给出的三道题中任选一题作答,如果多做,则按所做的第一题计分【选修3-3】(15分)
18.(5分)下列说法中正确的是( )
A.布朗运动并不是液体分子的运动,但它说明分子永不停息地做无规则运动
B.叶面上的小露珠呈球形是由于液体表面张力的作用
C.液晶显示器是利用了液晶对光具有各向异性的特点
D.当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小
【分析】依据布朗运动现象和实质判定A;
由表面张力的形成原因判定B;
液晶的特征是具有光学异性,故可以制作显示器;
依据分子力做功判定分析势能;
【解答】解:
A、布朗运动是悬浮在液体中的固体小颗粒的运动,它说明液体分子永不停息地做无规则运动。故A正确;
B、液体表面张力产生的原因是:液体跟气体接触的表面存在一个薄层,叫做表面层,表面层里的分子比液体内部稀疏,分子间的距离比液体内部大一些,分子间的相互作用表现为引力。露珠的形成就是由于液体表面张力的作用,故B正确;
C、液晶显示器是利用了液晶对光具有各向异性的特点,故C正确;
D、当两分子间距离大于平衡位置的间距r0时,分子力表现为引力,故随分子间的距离增大,分子力做负功,分子势能增大,故D错误;
故选:ABC。
【点评】该题关键是掌握布朗运动的现象和实质;其次要会分析分子力随距离的变化,以及分子力做功与分子势能变化关系,这些是重点考查内容。
19.(10分)如图所示,在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内,用4cm高的水银柱封闭着51cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg。
①若缓慢对玻璃管加热,当水银柱上表面与管口刚好相平时,求管中气体的温度;
②若保持管内温度始终为33℃,现将水银缓慢注入管中,直到水银柱上表面与管口相平,求此时管中气体的压强。
【分析】(1)对气体加热的过程中,气体的压强不变,求出气体的状态参量,然后根据玻意耳定律和盖﹣吕萨克定律求出气体的温度。
(2)当水银柱上表面与管口相平,设水银柱的高度为H,管内气体经等温压缩,由玻意耳定律即可求出结果。
【解答】解:①设玻璃管横截面积为S,以管内封闭气体为研究对象,气体经等压膨胀:
初状态:V1=51S,T1=306K;
末状态:V2=53S,T2=?
由盖吕萨克定律:
解得:T2=318K
②当水银柱上表面与管口相平,设此时管中气体压强为p,水银柱的高度为H,管内气体经等温压缩,
初状态:V1=51S,p1=80cmHg
末状态:V2=(57﹣H)S,p2=(76+H)cmHg
由玻意耳定律:p1V1=p2V2
得:H=9cm
故:p2=85cmHg
答:①若缓慢对玻璃管加热,当水银柱上表面与管口刚好相平时,管中气体的温度是318K;
②若保持管内温度始终为33℃,现将水银缓慢注入管中,直到水银柱上表面与管口相平,此时管中气体的压强是85cmHg。
【点评】本题考查了应用理想气体状态方程求气体压强,分析清楚气体状态变化过程是正确解题的关键。
【选修3-4】(15分)
20.A、B两列简谐横波均沿x轴正向传播,在某时刻的波形分别如图中甲、乙所示,经过时间t(t小于A波的周期TA),这两列简谐横波的波形分别变为图中丙、丁所示,则A、B两列波的波速vA、vB之比可能是( )
A.1:1 B.2:1 C.1:2 D.3:1
E.1:3
【分析】由题,甲、丙图象反相,t小于A波的周期TA,说明A波经过了半个周期.B波的图象与原来重合,说明经过了整数倍周期.由图读出两波的波长,由题分别得到周期与时间的关系,由波速公式得到波速的关系式,再进行选择.
【解答】解:由图读出,A波波长为λA=24cm,甲图到丙图一定是半个周期,所以周期TA=2t;B波波长为λB=12cm,乙图与丁图的波形图相同,经过的时间一定是整数个周期,所以周期TB=,波速vA=,vB=,
得到vA:vB=1:n,所以A、B两列波的波速vA、vB之比可能是ACE,不可能的是B、D。
故选:ACE。
【点评】本题中知道两个时刻波形图,抓住经过半个周期时间,波形反相;经过整数倍周期时间,图象重合是关键.
21.有一玻璃球冠,右侧面镀银,光源S就在其对称轴上,如图所示,从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折射入玻璃球冠内,经右侧镀银面第一次反射恰能沿原路返回,若球面半径为R,玻璃折射率为,求光源S与球冠顶点M之间的距离SM为多大?
【分析】作出光路图,根据折射定律和几何关系,求出入射角和折射角,再由几何关系求解光源S与球心O之间的距离SO,从而得到SM.
【解答】解:如图所示,根据折射定律,有:
n=
根据反射定律,有:θ1=θ3
其中:θ3+θ2=90°
联立可得:θ1=60°,θ2=30°
由图,有:β=θ2=30°,α=θ1﹣β=30°
故:SO=R
故光源S与M间距:SN=SO﹣R=(﹣1)R≈0.73R
答:光源S与球冠顶点M之间的距离SM为0.73R.
【点评】处理几何光学相关的问题,关键是作出光路图,一定要用直尺准确作图,然后根据几何图形的特点求角或者线段的长度.
【选修3-5】(15分)
22.以下说法符合物理学史的是 ( )
A.普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元
B.康普顿效应表明光子具有能量
C.德布罗意把光的波粒二象性推广到实物粒子,认为实物粒子也具有波动性
D.汤姆逊通过α粒子散射实验,提出了原子具有核式结构
E.卢瑟福利用α粒子轰击氮核发现了质子,并预言了中子的存在
【分析】根据物理学史和常识解答,记住著名物理学家的主要贡献即可。
【解答】解:A、普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元,故A正确;
B、康普顿效应不仅表明了光子具有能量,还表明了光子具有动量,故B错误;
C、德布罗意把光的波粒二象性推广到实物粒子,认为实物粒子也具有波动性,故C正确;
D、卢瑟福在用α粒子轰击金箔的实验中发现了质子,并预言了中子的存在,提出原子核式结构学说,故D错误,E正确;
故选:ACE。
【点评】本题考查物理学史,是常识性问题,对于物理学上重大发现、发明、著名理论要加强记忆,这也是考试内容之一。
23.如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连。另一质量为m的小物块A以速度v0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计。(所有过程都在弹簧弹性限度范围内)求:
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比。
【分析】(1)A、B发生弹性碰撞,碰撞过程动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出碰后两物体的速度。
(2)在B压缩弹簧过程中,系统机械能守恒,由机械能守恒定律可以求出弹簧的弹性势能;当弹簧第一次伸长最长时,B、C两物体组成的系统动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出弹簧的弹性势能,然后求出弹簧的弹性势能之比。
【解答】解:(1)A、B发生弹性正碰,碰撞过程中,A、B组成的系统动量守恒、机械能守恒,以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得:
mv0=mvA+2mvB,
在碰撞过程中机械能守恒,由机械能守恒定律得:
mv02=mvA2+?2mvB2,
联立解得:vA=﹣v0,vB=v0;
(2)弹簧第一次压缩到最短时,B的速度为零,该过程机械能守恒,由机械能守恒定律得,弹簧的弹性势能:
EP=?2m?vB2=mv02,
从弹簧压缩最短到弹簧恢复原长时,B、C与弹簧组成的系统机械能守恒,
弹簧恢复原长时,B的速度vB=v0,速度方向向右,C的速度为零,
从弹簧恢复原长到弹簧第一次伸长最长时,B、C与弹簧组成的系统动量守恒、机械能守恒,
弹簧伸长最长时,B、C速度相等,以向右为正方向,由动量守恒定律得:
2mvB=(2m+2m)v′,
由机械能守恒定律得:
?2m?vB2=?(2m+2m)?v′2+EP′,
解得:EP′=mv02,
弹簧第一次压缩最短与第一次伸长最长时弹性势能之比:EP:EP′=2:1;
答:(1)A、B碰后瞬间,A的速度为v0,方向向右,B的速度为v0,方向向左;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比为2:1。
【点评】本题考查了物体的速度与弹簧弹性势能之比,应用动量守恒定律与机械能守恒定律即可正确解题,分析清楚物体运动过程是正确 解题的关键。
同课章节目录
