1.4 算法的概念和表示方法 课件(25张幻灯片)
文档属性
| 名称 | 1.4 算法的概念和表示方法 课件(25张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 958.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2019-06-27 00:00:00 | ||
图片预览







文档简介
课件25张PPT。算法和算法的表示
帮老师数人数小游戏解决某一问题可以有多种方法
解决问题时,我们需要进行分析问题、设计算法、得出结果、验证结果等步骤 算法是解决一个问题的步骤和方法小游戏告诉我们:
秦朝末年,楚汉相争。一次,韩信将1500名将士与楚王大将李锋交战。楚军不敌,败退回营,汉军也死伤四五百人,于是韩信整顿兵马也返回大本营。当行至一山坡,忽有后军来报,说有楚军骑兵追来。只见远方尘土飞扬,杀声震天。汉军本来已十分疲惫,这时队伍大哗。韩信兵马到坡顶,见来敌不足五百骑,便急速点兵迎敌。他命令士兵3人一排,结果多出2名;接着命令士兵5人一排,结果多出3名;他又命令士兵7人一排,结果又多出2名。韩信马上向将士们宣布:我军有1073名勇士,敌人不足五百,我们居高临下,以众击寡,一定能打败敌人。汉军本来就信服自己的统帅,这一来更相信韩信是“神仙下凡”、“神机妙算”。于是士气大振。楚军大败而逃。韩信点兵,多多益善故事由来“韩信点兵”问题:
今有士兵若干,每3人一列余2人、5人一列余3人、7人一列余2人、有士兵多少人?
这个问题又称“鬼谷算”、“秦王暗点兵”评选:最强逻辑组
老师提出问题后,能最快举手回答或展示问题结果的同学,为本小组赢得5分;
每个同学课堂自测的结果将为小组加分“韩信点兵”问题:
每3人一列余2人、5人一列余3人、7人一列余2人,韩信点了多少兵?
用数学方法转换“韩信点兵”问题:求整除3余2,整除5余3,整除7余2的最小自然数打开教学网站的任务导学,完成任务一1、2小题方程X=3n1+2
X=5n2+3
X=7n3+2建立数学模型: 用数学的方法分析,设要求的数为X,每次的列数分别为n1,n2,n3:可得联立方程组:方? 设所求的数为X,则X应满足:
X整除3余2
X整除5余3
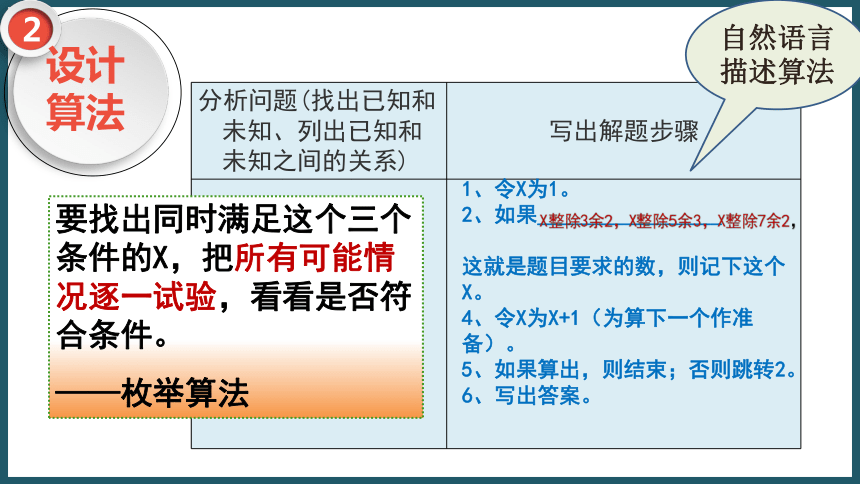
X整除7余21、令X为1。
2、如果_________________
这就是题目要求的数,则记下这个X。
4、令X为X+1(为算下一个作准备)。
5、如果算出,则结束;否则跳转2。
6、写出答案。要找出同时满足这个三个条件的X,把所有可能情况逐一试验,看看是否符合条件。
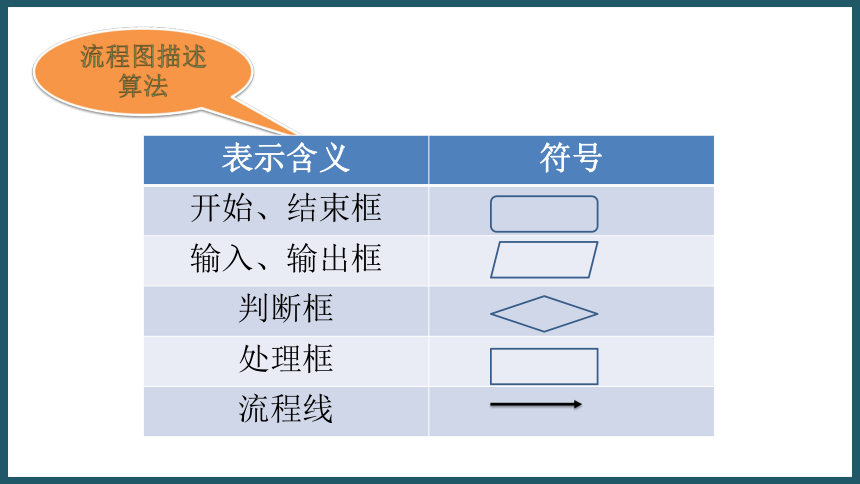
——枚举算法自然语言描述算法X整除3余2,X整除5余3,X整除7余2,流程图描述算法尝试完善算法流程图开始结束Y1、令X为1。
如果,X整除5余2,X整除7余4,这就是题目要求的数,则记下这个X。
3、令X为X+1(为算下一个作准备)。
4、如果算出,则结束;否则跳转2。
5、写出答案。1 ? XX+1?X输出XNX被3、5、7、整除后余数为2、3、2请尝试手工方式写出答案,完成任务一3、4小题问题牵移与扩大数据量后
“韩信点兵”深度问题:
求整除3余1,整除5余2,整除7余4,整除13余6,整除17余8的最小自然数 面对这个数据量很大问题,利用人工求解要耗费更多的时间和精力,而计算机由于超快的计算能力,最善于做相似的重复的处理操作。分析问题编写程序代码设计算法调试运行程序计算机解决问题的一般过程 程序设计语言:是人们与计算机交流的桥梁,通过它告诉计算机执行一系列操作,实现某种功能。
常用的计算机语言有C ,C++ ,Visual Basic ,JAVA,PYthon?等。开始X被3、5、7、整除后余数为2、3、2X+1?X输出X结束YNDim X As Integer
X=11 ? XPrivate Sub Command1_Click()Mod 是求余运算符End SubDo While not (X Mod 3= 2 and X Mod 5 = 3 and X Mod 7 = 2)
X=X+1
Loop print “韩信统御士兵数:” ;X编写程序解决韩信点兵问题:
计算机语言描述算法(或伪代码)利用VB调试运行问题1程序 韩信统御士兵数:?“韩信点兵”问题2:
求整除3余1,整除5余2,整除7余4,整除13余6,整除17余8的最小自然数能力提升组内成员互助,完成“韩信点兵”问题2比一比谁最快让你的程序飞起来!“韩信点兵”问题2:求整除3余1、整除5余2、整除7余4、整除13余6、整除17余8的最小自然数。 修改程序,调试运行,输出结果。士兵数:?分析问题、设计算法、得出结果、验算结果等
对题目进行解答、运算速度慢、不需要计算机等编写程序、调试程序、运算速度快等人工解题与计算机解题的异同:课堂自测打开教学网站做课堂自测题,选择组别并提交查看答题情况,进行自查自纠。人工解题过程体验,数学建模
分析问题,设计算法,编写代码,调试运行
算法的描述、结构,计算机语言
人工解题与计算机解题异同
韩信点兵问题
计算机解决问题的过程与方法本课小结阿尔法围棋(AlphaGo)是一款围棋人工智能程序。 业界人士透露,其实“大师”根本不会下棋,只会看图。这个图就是棋盘。简单来说,“大师”每次落子前会经历四步:
一、读取当前棋盘;
二、随机尝试走棋;
三、对每个走棋路线的结果进行输赢概率的计算;
四、把所有计算结果综合起来得出一个胜率最高的落子点。
基于计算机的超快计算能力,“大师”的强大可以说是必然的。
谢谢!计算机天生就是用来解决以前没有过的问题的。
----比尔盖茨
解决问题时,我们需要进行分析问题、设计算法、得出结果、验证结果等步骤 算法是解决一个问题的步骤和方法小游戏告诉我们:
秦朝末年,楚汉相争。一次,韩信将1500名将士与楚王大将李锋交战。楚军不敌,败退回营,汉军也死伤四五百人,于是韩信整顿兵马也返回大本营。当行至一山坡,忽有后军来报,说有楚军骑兵追来。只见远方尘土飞扬,杀声震天。汉军本来已十分疲惫,这时队伍大哗。韩信兵马到坡顶,见来敌不足五百骑,便急速点兵迎敌。他命令士兵3人一排,结果多出2名;接着命令士兵5人一排,结果多出3名;他又命令士兵7人一排,结果又多出2名。韩信马上向将士们宣布:我军有1073名勇士,敌人不足五百,我们居高临下,以众击寡,一定能打败敌人。汉军本来就信服自己的统帅,这一来更相信韩信是“神仙下凡”、“神机妙算”。于是士气大振。楚军大败而逃。韩信点兵,多多益善故事由来“韩信点兵”问题:
今有士兵若干,每3人一列余2人、5人一列余3人、7人一列余2人、有士兵多少人?
这个问题又称“鬼谷算”、“秦王暗点兵”评选:最强逻辑组
老师提出问题后,能最快举手回答或展示问题结果的同学,为本小组赢得5分;
每个同学课堂自测的结果将为小组加分“韩信点兵”问题:
每3人一列余2人、5人一列余3人、7人一列余2人,韩信点了多少兵?
用数学方法转换“韩信点兵”问题:求整除3余2,整除5余3,整除7余2的最小自然数打开教学网站的任务导学,完成任务一1、2小题方程X=3n1+2
X=5n2+3
X=7n3+2建立数学模型: 用数学的方法分析,设要求的数为X,每次的列数分别为n1,n2,n3:可得联立方程组:方? 设所求的数为X,则X应满足:
X整除3余2
X整除5余3
X整除7余21、令X为1。
2、如果_________________
这就是题目要求的数,则记下这个X。
4、令X为X+1(为算下一个作准备)。
5、如果算出,则结束;否则跳转2。
6、写出答案。要找出同时满足这个三个条件的X,把所有可能情况逐一试验,看看是否符合条件。
——枚举算法自然语言描述算法X整除3余2,X整除5余3,X整除7余2,流程图描述算法尝试完善算法流程图开始结束Y1、令X为1。
如果,X整除5余2,X整除7余4,这就是题目要求的数,则记下这个X。
3、令X为X+1(为算下一个作准备)。
4、如果算出,则结束;否则跳转2。
5、写出答案。1 ? XX+1?X输出XNX被3、5、7、整除后余数为2、3、2请尝试手工方式写出答案,完成任务一3、4小题问题牵移与扩大数据量后
“韩信点兵”深度问题:
求整除3余1,整除5余2,整除7余4,整除13余6,整除17余8的最小自然数 面对这个数据量很大问题,利用人工求解要耗费更多的时间和精力,而计算机由于超快的计算能力,最善于做相似的重复的处理操作。分析问题编写程序代码设计算法调试运行程序计算机解决问题的一般过程 程序设计语言:是人们与计算机交流的桥梁,通过它告诉计算机执行一系列操作,实现某种功能。
常用的计算机语言有C ,C++ ,Visual Basic ,JAVA,PYthon?等。开始X被3、5、7、整除后余数为2、3、2X+1?X输出X结束YNDim X As Integer
X=11 ? XPrivate Sub Command1_Click()Mod 是求余运算符End SubDo While not (X Mod 3= 2 and X Mod 5 = 3 and X Mod 7 = 2)
X=X+1
Loop print “韩信统御士兵数:” ;X编写程序解决韩信点兵问题:
计算机语言描述算法(或伪代码)利用VB调试运行问题1程序 韩信统御士兵数:?“韩信点兵”问题2:
求整除3余1,整除5余2,整除7余4,整除13余6,整除17余8的最小自然数能力提升组内成员互助,完成“韩信点兵”问题2比一比谁最快让你的程序飞起来!“韩信点兵”问题2:求整除3余1、整除5余2、整除7余4、整除13余6、整除17余8的最小自然数。 修改程序,调试运行,输出结果。士兵数:?分析问题、设计算法、得出结果、验算结果等
对题目进行解答、运算速度慢、不需要计算机等编写程序、调试程序、运算速度快等人工解题与计算机解题的异同:课堂自测打开教学网站做课堂自测题,选择组别并提交查看答题情况,进行自查自纠。人工解题过程体验,数学建模
分析问题,设计算法,编写代码,调试运行
算法的描述、结构,计算机语言
人工解题与计算机解题异同
韩信点兵问题
计算机解决问题的过程与方法本课小结阿尔法围棋(AlphaGo)是一款围棋人工智能程序。 业界人士透露,其实“大师”根本不会下棋,只会看图。这个图就是棋盘。简单来说,“大师”每次落子前会经历四步:
一、读取当前棋盘;
二、随机尝试走棋;
三、对每个走棋路线的结果进行输赢概率的计算;
四、把所有计算结果综合起来得出一个胜率最高的落子点。
基于计算机的超快计算能力,“大师”的强大可以说是必然的。
谢谢!计算机天生就是用来解决以前没有过的问题的。
----比尔盖茨
同课章节目录
- 第一章 算法和算法的表示
- 1.1 使用计算机解决问题的一般过程
- 1.2 确定解决问题的方法
- 1.3 把解决问题的方法步骤化
- 1.4 算法的概念和表示方法
- 第二章 算法实例
- 2.1 枚举算法
- 2.2 解析算法
- 2.3 排序
- 2.4 查找
- 第三章 面向对象程序设计的基本知识
- 3.1 面向对象程序设计方法简介
- 3.2 在可视化的程序设计环境VB中建立一个应用程序
- 第四章 VB程序设计初步
- 4.1 基本数据类型、常量、变量
- 4.2 基本运算和表达式
- 4.3 语句
- 4.4 过程和函数
- 第五章 算法实例的程序实现
- 5.1 枚举算法的程序实现
- 5.2 解析算法的程序实现
- 5.3 排序算法的程序实现
- 5.4 查找算法的程序实现
- 5.5 递归算法实例及程序实现
- 非试题类资料
