高中数学必修四知识讲解,巩固练习(复习补习,期末复习资料):09【基础】正弦函数、余弦函数的图象
文档属性
| 名称 | 高中数学必修四知识讲解,巩固练习(复习补习,期末复习资料):09【基础】正弦函数、余弦函数的图象 |

|
|
| 格式 | zip | ||
| 文件大小 | 695.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-28 00:00:00 | ||
图片预览


文档简介
【基础】正弦函数、余弦函数的图象
正弦函数、余弦函数的图象
【学习目标】
1.了解作正弦函数、余弦函数图象的三种方法;
2.掌握三角函数图象的作用,会用“五点法”作出正弦函数和余弦函数的图象。
【要点梳理】
要点一:正弦函数、余弦函数图象的画法
1.描点法:
按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法。
2.几何法
利用三角函数线作出正弦函数和余弦函数在内的图象,再通过平移得到和的图象。
3.五点法
先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点,再利用光滑曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。
在确定正弦函数在上的图象形状时,起关键作用的五个点是
要点诠释:
(1)熟记正弦函数、余弦函数图象起关键作用的五点。
(2)若,可先作出正弦函数、余弦函数在上的图象,然后通过左、右平移可得到和的图象。
(3)由诱导公式,故的图象也可以将的图象上所有点向左平移个单位长度得到。
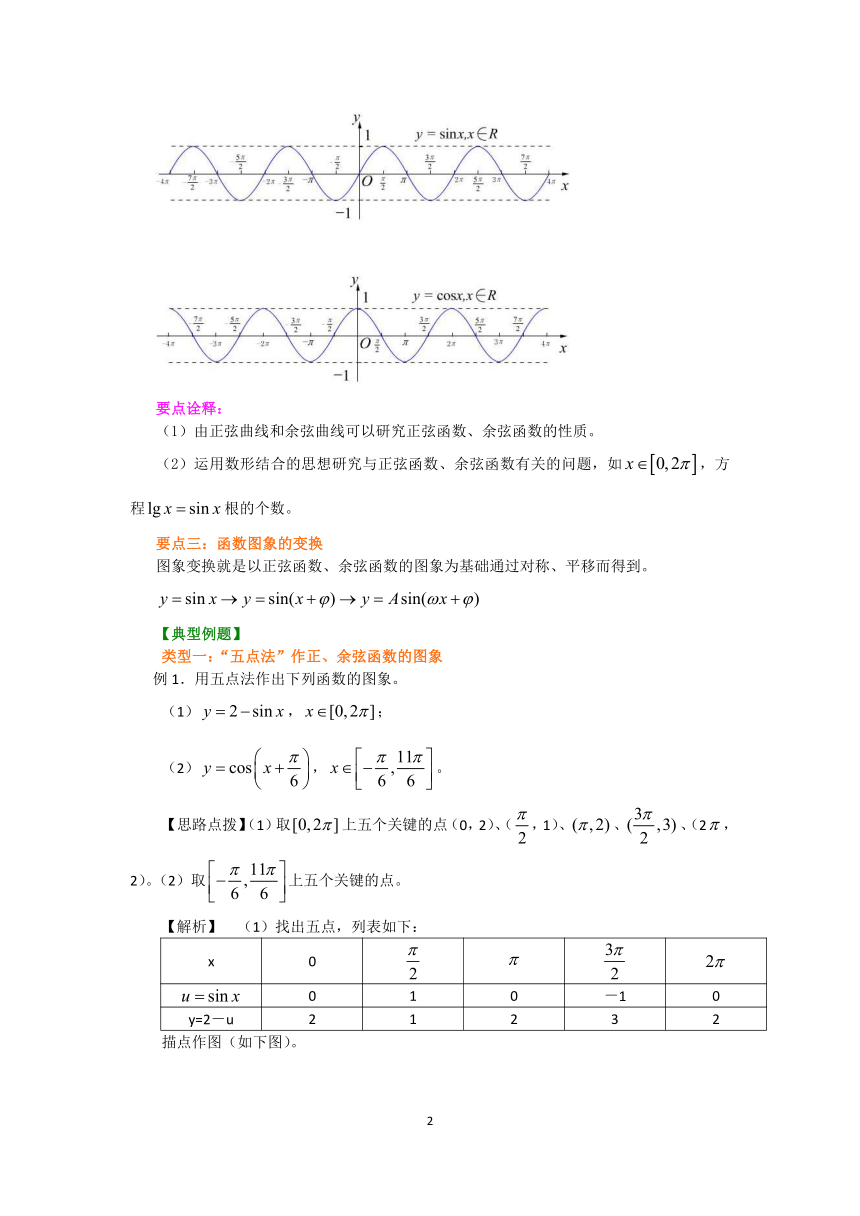
要点二:正弦曲线、余弦曲线
(1)定义:正弦函数和余弦函数的图象分别叫做正弦曲线和余弦曲线。
(2)图象
要点诠释:
(1)由正弦曲线和余弦曲线可以研究正弦函数、余弦函数的性质。
(2)运用数形结合的思想研究与正弦函数、余弦函数有关的问题,如,方程根的个数。
要点三:函数图象的变换
图象变换就是以正弦函数、余弦函数的图象为基础通过对称、平移而得到。
【典型例题】
类型一:“五点法”作正、余弦函数的图象
例1.用五点法作出下列函数的图象。
(1),;
(2),。
【思路点拨】(1)取上五个关键的点(0,2)、(,1)、、、(2,2)。(2)取上五个关键的点。
【解析】 (1)找出五点,列表如下:
x
0
0
1
0
-1
0
y=2-u
2
1
2
3
2
描点作图(如下图)。
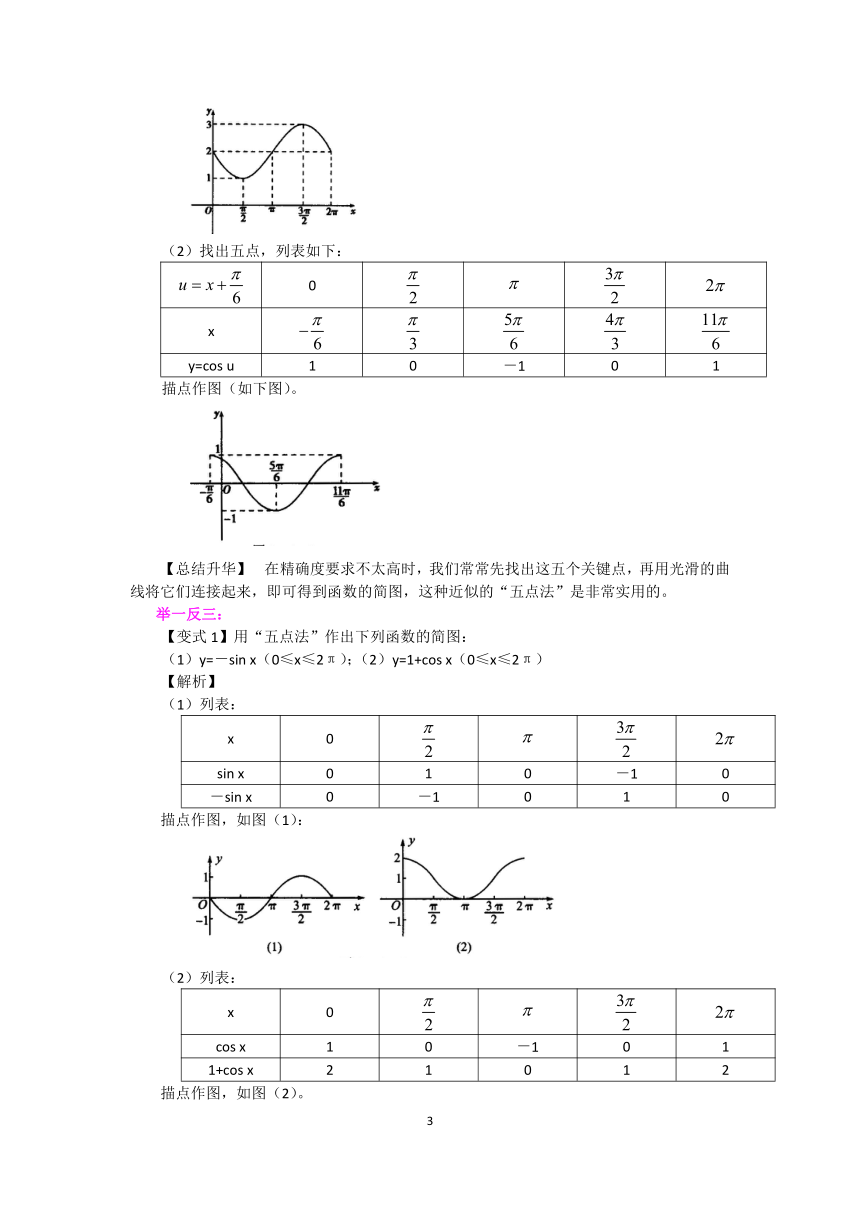
(2)找出五点,列表如下:
0
x
y=cos u
1
0
-1
0
1
描点作图(如下图)。
【总结升华】 在精确度要求不太高时,我们常常先找出这五个关键点,再用光滑的曲线将它们连接起来,即可得到函数的简图,这种近似的“五点法”是非常实用的。
举一反三:
【变式1】用“五点法”作出下列函数的简图:
(1)y=-sin x(0≤x≤2π);(2)y=1+cos x(0≤x≤2π)
【解析】
(1)列表:
x
0
sin x
0
1
0
-1
0
-sin x
0
-1
0
1
0
描点作图,如图(1):
(2)列表:
x
0
cos x
1
0
-1
0
1
1+cos x
2
1
0
1
2
描点作图,如图(2)。
类型二:利用图象变换作出函数的图象
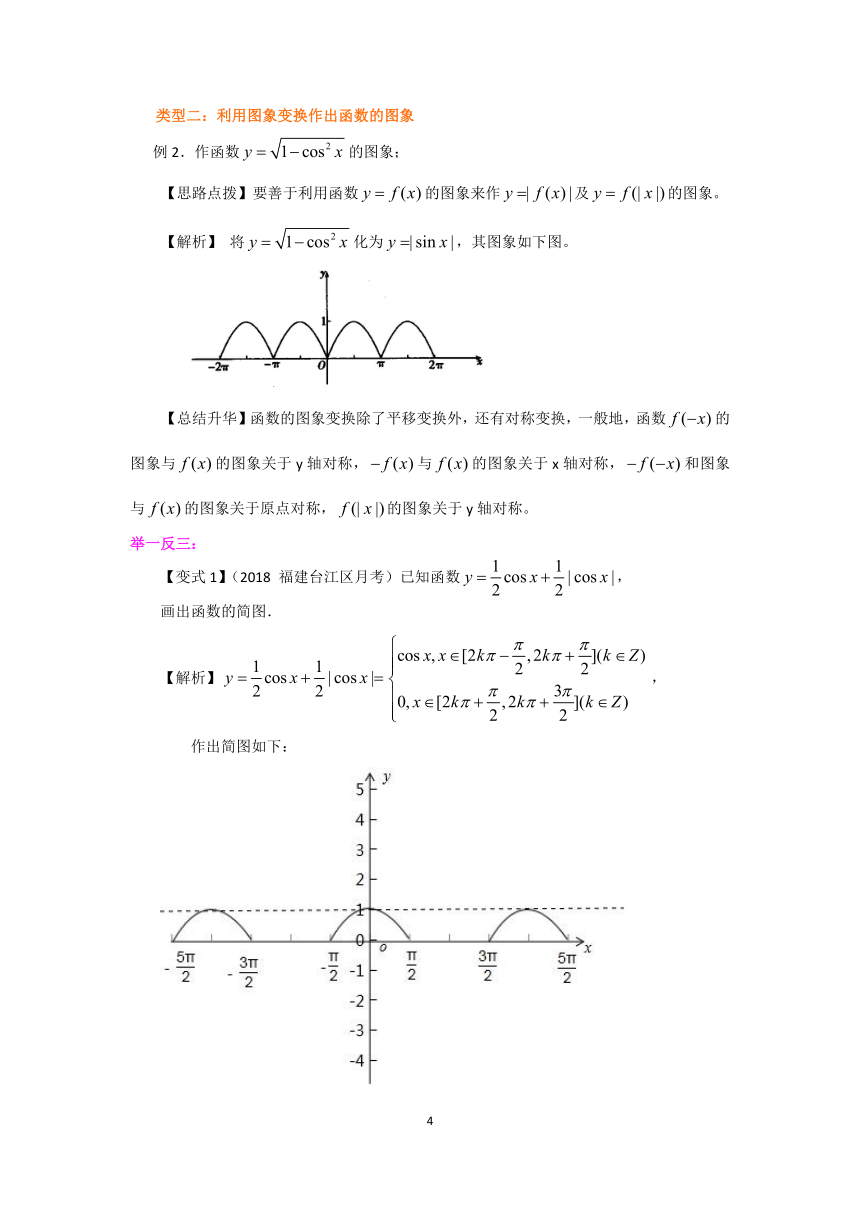
例2.作函数的图象;
【思路点拨】要善于利用函数的图象来作及的图象。
【解析】 将化为,其图象如下图。
【总结升华】函数的图象变换除了平移变换外,还有对称变换,一般地,函数的图象与的图象关于y轴对称,与的图象关于x轴对称,和图象与的图象关于原点对称,的图象关于y轴对称。
举一反三:
【变式1】(2018 福建台江区月考)已知函数,
画出函数的简图.
【解析】,
作出简图如下:
类型三:利用函数图象解简单的三角不等式
例3.画出正弦函数(x∈R)的简图,并根据图象写出:
(1)时x的集合;
(2)时x的集合。
【思路点拨】用“五点法”作出y=sin x的简图。
【解析】
(1)过点作x轴的平行线,从图象中看出:在[0,2π]区间与正弦曲线交于、两点,在[0,2π]区间内,时x的集合为。当x∈R时,若,则x的集合为。
(2)过、两点分别作x轴的平行线,从图象中看出:在[0,2π]区间,它们分别与正弦曲线交于,点和,点,那么当时,x的集合为
或
。
【总结升华】利用三角函数的图象或三角函数线,都可解简单的不等式,但需注意解的完整性,此外数形结合是重要的数学思想,它能把抽象的数学式子转化为形象直观的图象,平时解题时要灵活运用。
举一反三:
【变式1】(2017春 四川资阳月考)利用正弦函数图象解下列不等式:
(1);
(2)
(3);
(4).
【解析】作出函数y=sin x的图象,如图所示:
由图可得:(1)时,,k∈Z,即原不等式的解集为,k∈Z;
(2)时,,k∈Z,即原不等式的解集为,k∈Z;
(3)时,,k∈Z,即,k∈Z,即原不等式的解集为,k∈Z;
(4)时,,k∈Z,即, k∈Z,即原不等式的解集为, k∈Z.
类型四:三角函数图象的应用
例4.(1)(2017春 陕西宝塔区月考)求在区间[-π,π]内解的个数.
(2)若,则与3的大小关系为( )
A. B.
C. D.与的取值有关
【思路点拨】(1)作出函数y=sin x与的函数图象,观察图象交点个数.(2)作出与的函数图象,利用数形结合可得.
【答案】(1)4;(2)D
【解析】(1)函数y=sin x与的图象交点个数等于方程解的个数.
在同一坐标系内作出两个函数y=sin x,在[-π,π]内的图象,如图所示.由图象不难看出,它们有4个交点.
所以方程在[-π,π]内有4个解.
(2)作图(如下图),观察函数,在内的图象可知与的大小关系与的取值有关.
举一反三:
【变式1】下列各式中正确的为( )
A. B.
C. D.
【答案】C
【巩固练习】
1.以下对正弦函数y=sin x的图象描述不正确的是( )
A.在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同
B.介于直线y=1与直线y=-1之间
C.关于x轴对称
D.与y轴仅有一个交点
2.用五点法作y=2sin2x的图象时,首先应描出的五点的横坐标可以是( )
A.0,,π,,2π B.0,,,,π
C.0,π,2π,3π,4π D.0,,,,
3.函数在区间的简图是( )
4.y=cos x,x∈[0,2π]的图象与直线的交点的个数为( )
A.0 B.1 C.2 D.3
5.方程|x|=cos x在(-∞,+∞)内( )
A.没有根 B.有且仅有一个根 C.有且仅有两个根 D.有无穷多个根
6.要得到函数的图象,只需将函数的图象( ).
A. 向右平移个单位 B. 向右平移个单位
C. 向左平移个单位 D. 向左平移个单位
7.设函数,x∈R,对于以下三个结论:
①函数的值域是[-1,1] ②当且仅当(k∈Z)时,取得最大值1 ③当且仅当2kπ+π<x<2kπ+(k∈Z)时,.
根据函数的图象判断其中正确结论的个数是( )
A.0 B.1 C.2 D.3
8.已知k<―4,则函数y=cos2x+k (cos x―1)的最小值是( )
A.1 B.―1 C.2k+1 D.―2k+1
9.函数y=cos x的图象可以通过将y=sin x的图象________而得到.
10.下列函数图象相同的序号是________.
①y=cos x与y=cos (π+x);
②与;
③y=sin x与y=sin (-x);
④y=sin (2π+x)与y=sin x.
11.若2sin x+3=a,则实数a的取值范围是________.
12.(2018 江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是________.
13.(2017秋 山东潍坊期中)画出下列函数的简图:
(1)y=1-sin x,x∈[0,2π];
(2)y=3cos x+1,x∈[0,2π].
14.(2017 河北邢台月考)利用图象变换作出下列函数的简图:y=1-cosx.
【答案与解析】
1.【答案】C
【解析】由三角函数y=sin x的图象知,它不关于x轴对称.
2.【答案】B
【解析】2x分别取0,,π,,2π.
3.【答案】A
4.【答案】C
【解析】y=cos x,x∈[0,2π]的图象与直线的交点的个数,即方程在区间[0,2π]上的解的个数.
由在区间[0,2π]上的解为,或,
可得方程在区间[0,2π]上的解的个数为2,
故选:C.
5.【答案】C
【解析】求解方程|x|=cos x在(-∞,+∞)内根的个数问题,可转化为求解函数和在(-∞,+∞)内的交点个数问题.和的图象如图所示,显然有两交点,即原方程有且仅有两个根.
6.【答案】A
7.【答案】C
【解析】 作出正弦函数y=sin x,x∈R的图象(如下图),从图中可以看出①②正确,③错误.
8.【答案】A
【解析】 y=cos2x+k (cos x―1)=2cos2x+kcos x―(k+1).令t=cos x(t∈[―1,1]),则y=2t2+kt―(k+1),对称轴.∵k<-4,∴,∴函数y=2t2+kt―(k+1)在[―1,1]内为单递减函数.当t=1,即cos x=1时,函数有最小值1.故选A.
9.【答案】向左平移个单位长度
【解析】因为,故
.
10.【答案】④
【解析】根据诱导公式,只有sin (2π+x)=sin x成立.
11.【答案】[1,5]
【解析】∵2sin x+3=a,
∴
∵sin x∈[-1,1]
∴,
解得1≤a≤5;
故实数a的取值范围为[1,5],
故答案为:[1,5].
12.【答案】7.
【解析】画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:
由图可知,共7个交点.
故答案为:7.
13.【解析】(1)列表如下:
画出图形,如图:
(2)列表为
函数图象如下:
14.【解析】先作出y=cosx的图象,然后利用对称作出y=-cosx的图象,最后向上平移1个单位即可,如下图.
正弦函数、余弦函数的图象
【学习目标】
1.了解作正弦函数、余弦函数图象的三种方法;
2.掌握三角函数图象的作用,会用“五点法”作出正弦函数和余弦函数的图象。
【要点梳理】
要点一:正弦函数、余弦函数图象的画法
1.描点法:
按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法。
2.几何法
利用三角函数线作出正弦函数和余弦函数在内的图象,再通过平移得到和的图象。
3.五点法
先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点,再利用光滑曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。
在确定正弦函数在上的图象形状时,起关键作用的五个点是
要点诠释:
(1)熟记正弦函数、余弦函数图象起关键作用的五点。
(2)若,可先作出正弦函数、余弦函数在上的图象,然后通过左、右平移可得到和的图象。
(3)由诱导公式,故的图象也可以将的图象上所有点向左平移个单位长度得到。
要点二:正弦曲线、余弦曲线
(1)定义:正弦函数和余弦函数的图象分别叫做正弦曲线和余弦曲线。
(2)图象
要点诠释:
(1)由正弦曲线和余弦曲线可以研究正弦函数、余弦函数的性质。
(2)运用数形结合的思想研究与正弦函数、余弦函数有关的问题,如,方程根的个数。
要点三:函数图象的变换
图象变换就是以正弦函数、余弦函数的图象为基础通过对称、平移而得到。
【典型例题】
类型一:“五点法”作正、余弦函数的图象
例1.用五点法作出下列函数的图象。
(1),;
(2),。
【思路点拨】(1)取上五个关键的点(0,2)、(,1)、、、(2,2)。(2)取上五个关键的点。
【解析】 (1)找出五点,列表如下:
x
0
0
1
0
-1
0
y=2-u
2
1
2
3
2
描点作图(如下图)。
(2)找出五点,列表如下:
0
x
y=cos u
1
0
-1
0
1
描点作图(如下图)。
【总结升华】 在精确度要求不太高时,我们常常先找出这五个关键点,再用光滑的曲线将它们连接起来,即可得到函数的简图,这种近似的“五点法”是非常实用的。
举一反三:
【变式1】用“五点法”作出下列函数的简图:
(1)y=-sin x(0≤x≤2π);(2)y=1+cos x(0≤x≤2π)
【解析】
(1)列表:
x
0
sin x
0
1
0
-1
0
-sin x
0
-1
0
1
0
描点作图,如图(1):
(2)列表:
x
0
cos x
1
0
-1
0
1
1+cos x
2
1
0
1
2
描点作图,如图(2)。
类型二:利用图象变换作出函数的图象
例2.作函数的图象;
【思路点拨】要善于利用函数的图象来作及的图象。
【解析】 将化为,其图象如下图。
【总结升华】函数的图象变换除了平移变换外,还有对称变换,一般地,函数的图象与的图象关于y轴对称,与的图象关于x轴对称,和图象与的图象关于原点对称,的图象关于y轴对称。
举一反三:
【变式1】(2018 福建台江区月考)已知函数,
画出函数的简图.
【解析】,
作出简图如下:
类型三:利用函数图象解简单的三角不等式
例3.画出正弦函数(x∈R)的简图,并根据图象写出:
(1)时x的集合;
(2)时x的集合。
【思路点拨】用“五点法”作出y=sin x的简图。
【解析】
(1)过点作x轴的平行线,从图象中看出:在[0,2π]区间与正弦曲线交于、两点,在[0,2π]区间内,时x的集合为。当x∈R时,若,则x的集合为。
(2)过、两点分别作x轴的平行线,从图象中看出:在[0,2π]区间,它们分别与正弦曲线交于,点和,点,那么当时,x的集合为
或
。
【总结升华】利用三角函数的图象或三角函数线,都可解简单的不等式,但需注意解的完整性,此外数形结合是重要的数学思想,它能把抽象的数学式子转化为形象直观的图象,平时解题时要灵活运用。
举一反三:
【变式1】(2017春 四川资阳月考)利用正弦函数图象解下列不等式:
(1);
(2)
(3);
(4).
【解析】作出函数y=sin x的图象,如图所示:
由图可得:(1)时,,k∈Z,即原不等式的解集为,k∈Z;
(2)时,,k∈Z,即原不等式的解集为,k∈Z;
(3)时,,k∈Z,即,k∈Z,即原不等式的解集为,k∈Z;
(4)时,,k∈Z,即, k∈Z,即原不等式的解集为, k∈Z.
类型四:三角函数图象的应用
例4.(1)(2017春 陕西宝塔区月考)求在区间[-π,π]内解的个数.
(2)若,则与3的大小关系为( )
A. B.
C. D.与的取值有关
【思路点拨】(1)作出函数y=sin x与的函数图象,观察图象交点个数.(2)作出与的函数图象,利用数形结合可得.
【答案】(1)4;(2)D
【解析】(1)函数y=sin x与的图象交点个数等于方程解的个数.
在同一坐标系内作出两个函数y=sin x,在[-π,π]内的图象,如图所示.由图象不难看出,它们有4个交点.
所以方程在[-π,π]内有4个解.
(2)作图(如下图),观察函数,在内的图象可知与的大小关系与的取值有关.
举一反三:
【变式1】下列各式中正确的为( )
A. B.
C. D.
【答案】C
【巩固练习】
1.以下对正弦函数y=sin x的图象描述不正确的是( )
A.在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同
B.介于直线y=1与直线y=-1之间
C.关于x轴对称
D.与y轴仅有一个交点
2.用五点法作y=2sin2x的图象时,首先应描出的五点的横坐标可以是( )
A.0,,π,,2π B.0,,,,π
C.0,π,2π,3π,4π D.0,,,,
3.函数在区间的简图是( )
4.y=cos x,x∈[0,2π]的图象与直线的交点的个数为( )
A.0 B.1 C.2 D.3
5.方程|x|=cos x在(-∞,+∞)内( )
A.没有根 B.有且仅有一个根 C.有且仅有两个根 D.有无穷多个根
6.要得到函数的图象,只需将函数的图象( ).
A. 向右平移个单位 B. 向右平移个单位
C. 向左平移个单位 D. 向左平移个单位
7.设函数,x∈R,对于以下三个结论:
①函数的值域是[-1,1] ②当且仅当(k∈Z)时,取得最大值1 ③当且仅当2kπ+π<x<2kπ+(k∈Z)时,.
根据函数的图象判断其中正确结论的个数是( )
A.0 B.1 C.2 D.3
8.已知k<―4,则函数y=cos2x+k (cos x―1)的最小值是( )
A.1 B.―1 C.2k+1 D.―2k+1
9.函数y=cos x的图象可以通过将y=sin x的图象________而得到.
10.下列函数图象相同的序号是________.
①y=cos x与y=cos (π+x);
②与;
③y=sin x与y=sin (-x);
④y=sin (2π+x)与y=sin x.
11.若2sin x+3=a,则实数a的取值范围是________.
12.(2018 江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是________.
13.(2017秋 山东潍坊期中)画出下列函数的简图:
(1)y=1-sin x,x∈[0,2π];
(2)y=3cos x+1,x∈[0,2π].
14.(2017 河北邢台月考)利用图象变换作出下列函数的简图:y=1-cosx.
【答案与解析】
1.【答案】C
【解析】由三角函数y=sin x的图象知,它不关于x轴对称.
2.【答案】B
【解析】2x分别取0,,π,,2π.
3.【答案】A
4.【答案】C
【解析】y=cos x,x∈[0,2π]的图象与直线的交点的个数,即方程在区间[0,2π]上的解的个数.
由在区间[0,2π]上的解为,或,
可得方程在区间[0,2π]上的解的个数为2,
故选:C.
5.【答案】C
【解析】求解方程|x|=cos x在(-∞,+∞)内根的个数问题,可转化为求解函数和在(-∞,+∞)内的交点个数问题.和的图象如图所示,显然有两交点,即原方程有且仅有两个根.
6.【答案】A
7.【答案】C
【解析】 作出正弦函数y=sin x,x∈R的图象(如下图),从图中可以看出①②正确,③错误.
8.【答案】A
【解析】 y=cos2x+k (cos x―1)=2cos2x+kcos x―(k+1).令t=cos x(t∈[―1,1]),则y=2t2+kt―(k+1),对称轴.∵k<-4,∴,∴函数y=2t2+kt―(k+1)在[―1,1]内为单递减函数.当t=1,即cos x=1时,函数有最小值1.故选A.
9.【答案】向左平移个单位长度
【解析】因为,故
.
10.【答案】④
【解析】根据诱导公式,只有sin (2π+x)=sin x成立.
11.【答案】[1,5]
【解析】∵2sin x+3=a,
∴
∵sin x∈[-1,1]
∴,
解得1≤a≤5;
故实数a的取值范围为[1,5],
故答案为:[1,5].
12.【答案】7.
【解析】画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:
由图可知,共7个交点.
故答案为:7.
13.【解析】(1)列表如下:
画出图形,如图:
(2)列表为
函数图象如下:
14.【解析】先作出y=cosx的图象,然后利用对称作出y=-cosx的图象,最后向上平移1个单位即可,如下图.
