16.4 碰撞 :21张PPT
文档属性
| 名称 | 16.4 碰撞 :21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-06-27 16:49:15 | ||
图片预览







文档简介
课件21张PPT。1. 了解弹性碰撞、非弹性碰撞和完全弹性碰撞。会应用动量、能量的观点综合分析、解决一维碰撞问题。
2.了解对心碰撞和非对心碰撞。
3. 了解散射和中子的发现过程,体会理论对实践的指导作用,进一步了解动量守恒定律的普适性。
4. 加深对动量守恒定律和机械能守恒定律的理解,能运用这两个字解决一些简单的与生产、生活相关的实际问题。
【重点难点】
1.应用动量、能量的观点综合分析、解决一维碰撞问题。
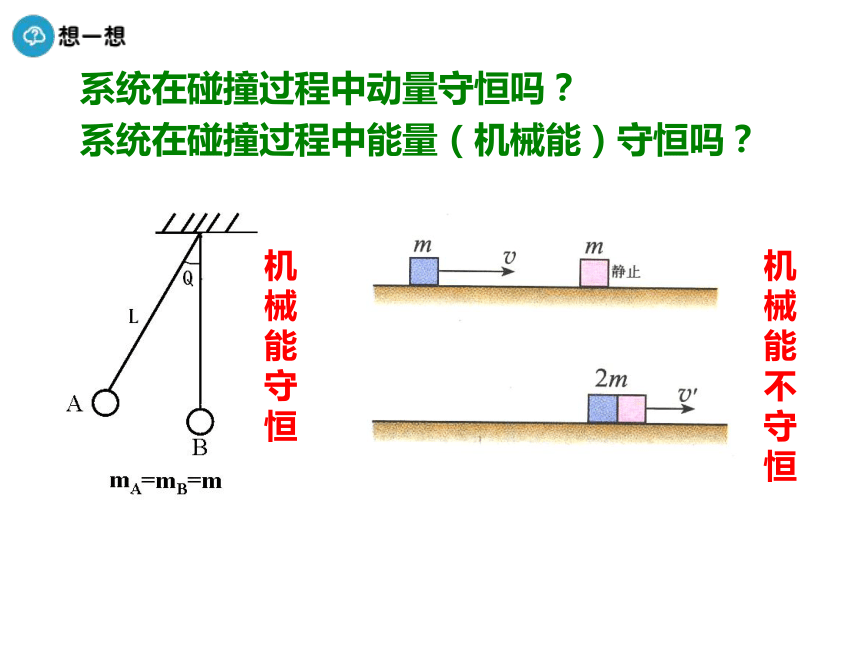
2.理解动量守恒定律和机械能守恒定律及其应用。非弹性碰撞与完全非弹性碰撞系统在碰撞过程中动量守恒吗?系统在碰撞过程中能量(机械能)守恒吗?机械能守恒机械能不守恒一、弹性碰撞和非弹性碰撞1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。例如钢球、玻璃球的碰撞2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。例如木制品、橡皮泥球的碰撞3. 完全非弹性碰撞:碰撞后两物体连在一起运动的现象。系统机械能损失最多。例如橡皮泥球之间的碰撞碰撞的类型总结: 弹性碰撞:碰撞过程中机械能守恒的碰撞。
特点:动量守恒,动能守恒,碰后分开。 2. 非弹性碰撞:碰撞过程中有能量的损失,机械能不守恒的碰撞。
特点:动量守恒,动能有损失,碰后不一定分开。3. 完全非弹性碰撞:非弹性碰撞中的一种。
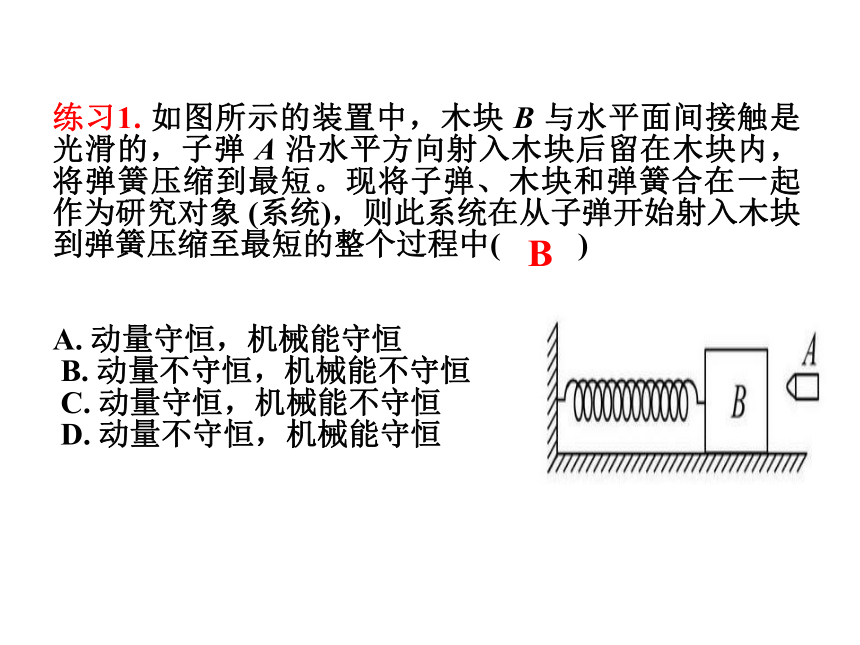
特点:动量守恒,动能损失最大,动能转化为其它能量,如内能、重力势能、弹性势能、磁场能、电场能等,碰后粘合在一起运动。练习1. 如图所示的装置中,木块 B 与水平面间接触是光滑的,子弹 A 沿水平方向射入木块后留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作为研究对象 (系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中( )
A. 动量守恒,机械能守恒
B. 动量不守恒,机械能不守恒
C. 动量守恒,机械能不守恒
D. 动量不守恒,机械能守恒BP18思考与讨论
……我们的任务是得出用m1、m2、v1表达v1 ′和v2 ′的公式。
碰撞过程都要遵从动量守恒定律……弹性碰撞中没有机械能损失……两个方程联立,把v1′和v2′作为未知量解出来就可以了。二、弹性正碰的研究弹性碰撞公式?由动量守恒得: m1V1= m1V1′ + m2V2 ′ ……………(1)由系统动能守恒联立①②式得:讨论: 1. 若 m1 = m2质量相等的两物体
弹性碰撞后交换速度2. 若 m1 << m2 3. 若m1 >>m2碰撞后第一个物体被撞了回去,以原来的速率向反方向运动,而第二个物体仍然静止碰撞后第一个物体的速度没有变化,而第二个物体以2v0的速度被撞出去练习2.在光滑水平面上有三个完全相同的小球,它们成一条直线,2、3小球静止,并靠在一起,1球以速度v0射向它们,如图所示,设碰撞为弹性碰撞,则碰撞后三个小球的速度可能是( )D2.非对心碰撞(斜碰):碰撞前后,物体的运动方向不在同一直线上。三、按运动形式分类:1.对心碰撞(正碰):碰撞前后,物体的运动方向在同一直线上。特点:发生对心碰撞的两个物体,碰撞前后的速度都是沿同一条直线,它们的动量也都沿这条直线,可以在这个方向上应用动量守恒定律。特点:对于非对心碰撞,由于碰撞前后速度不共线,故应该在相互垂直的两个方向上分别应用动量守恒定律四、散射--微观粒子的碰撞 微观粒子相互接近时并不发生直接接触,因此微观粒子的碰撞又叫做散射。粒子散射后,速度方向向着各个方向。散射是研究物质微观结构的重要方法。——卢瑟福做α粒子散射实验,提出了原子的核式结构学说。散射练习3:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。 mMv0vmMv0v根据动量守恒定律:
mv0= (m+M)vM动能增加,Fs = Mv2/2m动能减少,F’(s +d) = mv02/2 -mv2/2系统动能(机械能)减少:△E =Em-EM =Fd
= mv02/2 -mv2/2 - Mv2/2 =E内 从子弹进入木块前到刚好相对木块静止过程中根据动能定理:根据动能定理:1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做
弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 完全非弹性碰撞:碰撞后两物体连在一起运动的现象。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:系统动能损失最大
3. 对心碰撞和非对心碰撞
4.散射--微观粒子的碰撞
2.了解对心碰撞和非对心碰撞。
3. 了解散射和中子的发现过程,体会理论对实践的指导作用,进一步了解动量守恒定律的普适性。
4. 加深对动量守恒定律和机械能守恒定律的理解,能运用这两个字解决一些简单的与生产、生活相关的实际问题。
【重点难点】
1.应用动量、能量的观点综合分析、解决一维碰撞问题。
2.理解动量守恒定律和机械能守恒定律及其应用。非弹性碰撞与完全非弹性碰撞系统在碰撞过程中动量守恒吗?系统在碰撞过程中能量(机械能)守恒吗?机械能守恒机械能不守恒一、弹性碰撞和非弹性碰撞1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。例如钢球、玻璃球的碰撞2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。例如木制品、橡皮泥球的碰撞3. 完全非弹性碰撞:碰撞后两物体连在一起运动的现象。系统机械能损失最多。例如橡皮泥球之间的碰撞碰撞的类型总结: 弹性碰撞:碰撞过程中机械能守恒的碰撞。
特点:动量守恒,动能守恒,碰后分开。 2. 非弹性碰撞:碰撞过程中有能量的损失,机械能不守恒的碰撞。
特点:动量守恒,动能有损失,碰后不一定分开。3. 完全非弹性碰撞:非弹性碰撞中的一种。
特点:动量守恒,动能损失最大,动能转化为其它能量,如内能、重力势能、弹性势能、磁场能、电场能等,碰后粘合在一起运动。练习1. 如图所示的装置中,木块 B 与水平面间接触是光滑的,子弹 A 沿水平方向射入木块后留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作为研究对象 (系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中( )
A. 动量守恒,机械能守恒
B. 动量不守恒,机械能不守恒
C. 动量守恒,机械能不守恒
D. 动量不守恒,机械能守恒BP18思考与讨论
……我们的任务是得出用m1、m2、v1表达v1 ′和v2 ′的公式。
碰撞过程都要遵从动量守恒定律……弹性碰撞中没有机械能损失……两个方程联立,把v1′和v2′作为未知量解出来就可以了。二、弹性正碰的研究弹性碰撞公式?由动量守恒得: m1V1= m1V1′ + m2V2 ′ ……………(1)由系统动能守恒联立①②式得:讨论: 1. 若 m1 = m2质量相等的两物体
弹性碰撞后交换速度2. 若 m1 << m2 3. 若m1 >>m2碰撞后第一个物体被撞了回去,以原来的速率向反方向运动,而第二个物体仍然静止碰撞后第一个物体的速度没有变化,而第二个物体以2v0的速度被撞出去练习2.在光滑水平面上有三个完全相同的小球,它们成一条直线,2、3小球静止,并靠在一起,1球以速度v0射向它们,如图所示,设碰撞为弹性碰撞,则碰撞后三个小球的速度可能是( )D2.非对心碰撞(斜碰):碰撞前后,物体的运动方向不在同一直线上。三、按运动形式分类:1.对心碰撞(正碰):碰撞前后,物体的运动方向在同一直线上。特点:发生对心碰撞的两个物体,碰撞前后的速度都是沿同一条直线,它们的动量也都沿这条直线,可以在这个方向上应用动量守恒定律。特点:对于非对心碰撞,由于碰撞前后速度不共线,故应该在相互垂直的两个方向上分别应用动量守恒定律四、散射--微观粒子的碰撞 微观粒子相互接近时并不发生直接接触,因此微观粒子的碰撞又叫做散射。粒子散射后,速度方向向着各个方向。散射是研究物质微观结构的重要方法。——卢瑟福做α粒子散射实验,提出了原子的核式结构学说。散射练习3:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。 mMv0vmMv0v根据动量守恒定律:
mv0= (m+M)vM动能增加,Fs = Mv2/2m动能减少,F’(s +d) = mv02/2 -mv2/2系统动能(机械能)减少:△E =Em-EM =Fd
= mv02/2 -mv2/2 - Mv2/2 =E内 从子弹进入木块前到刚好相对木块静止过程中根据动能定理:根据动能定理:1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做
弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 完全非弹性碰撞:碰撞后两物体连在一起运动的现象。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:系统动能损失最大
3. 对心碰撞和非对心碰撞
4.散射--微观粒子的碰撞
