人教版 数学 必修四 2.4.1数量积的背景及意义(16张PPT)
文档属性
| 名称 | 人教版 数学 必修四 2.4.1数量积的背景及意义(16张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 195.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-29 00:00:00 | ||
图片预览






文档简介
课件16张PPT。θS
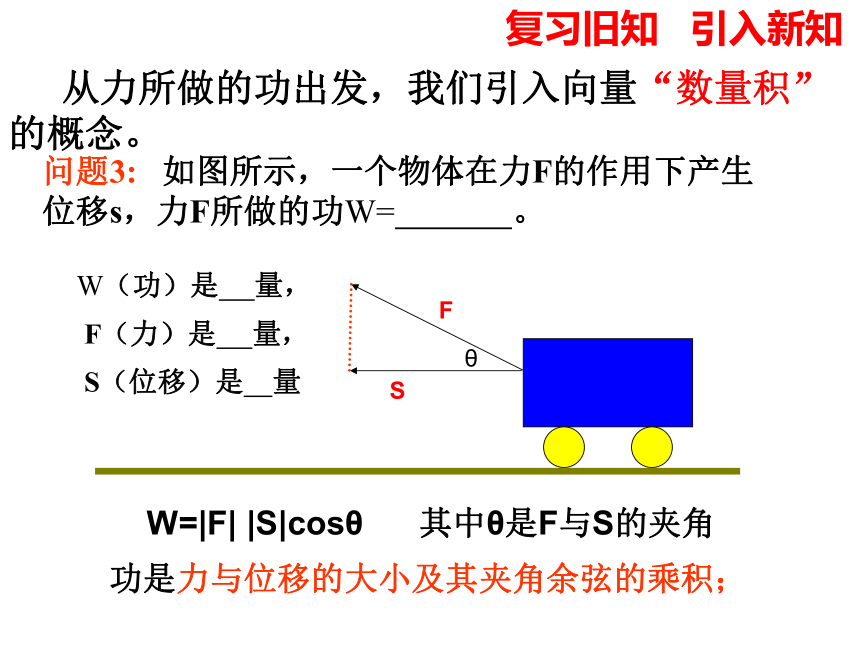
W=|F| |S|cosθ 其中θ是F与S的夹角 从力所做的功出发,我们引入向量“数量积”的概念。问题3: 如图所示,一个物体在力F的作用下产生位移s,力F所做的功W= 。 W(功)是 量,
F(力)是 量,
S(位移)是 量复习旧知 引入新知 功是力与位移的大小及其夹角余弦的乘积; 平面向量 2.4.1 平面向量数量积的 物理背景及其含义学习目标1. 在物理中功的概念的基础上,
理解向量数量积的概念及几何意义;
2. 掌握数量积的运算式及变式;
掌握并能熟练运用数量积的运算律;
掌握模长公式.1、向量的数量积的定义已知两个非零向量 与 ,它们的夹
角为θ, 我们把数量 叫做
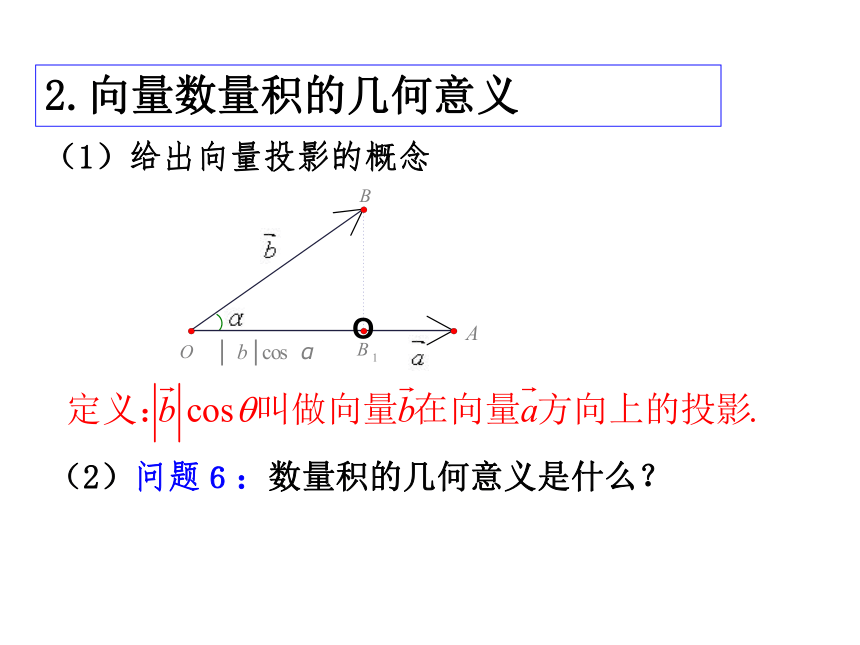
与 的数量积(或内积,点乘),即 注: 1、两向量的数量积是一个数量,而不是向量,符号由夹角决定2、 a · b不能写成a×b ,符号“·”在向量运算中不是乘号,不能省略.展示汇报 反馈点拨 例1、应用举例 问题 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?2.向量数量积的几何意义(1)给出向量投影的概念(2)问题6:数量积的几何意义是什么?O2、向量数量积的几何意义注:数量积的性质平面向量数量积的运算律 我们学过了实数乘法的哪些运算律?这些运算律对向量是否也适用? 经验证,数量积满足如下运算律(交换律)(数乘结合律)(分配律)4、数量积运算律说明:常用公式课本105页例2巩固训练 拓展提升例若 , ,且 , 则是多少?变式一:变式二:在△ABC中, 求,课堂小结:1、向量的数量积的定义2、向量数量积的几何意义课堂小结3、向量数量积的性质4、数量积运算律课堂小结:(交换律)(数乘结合律)(分配律)作业: 课本P108习题2.4A组1、2、3。
W=|F| |S|cosθ 其中θ是F与S的夹角 从力所做的功出发,我们引入向量“数量积”的概念。问题3: 如图所示,一个物体在力F的作用下产生位移s,力F所做的功W= 。 W(功)是 量,
F(力)是 量,
S(位移)是 量复习旧知 引入新知 功是力与位移的大小及其夹角余弦的乘积; 平面向量 2.4.1 平面向量数量积的 物理背景及其含义学习目标1. 在物理中功的概念的基础上,
理解向量数量积的概念及几何意义;
2. 掌握数量积的运算式及变式;
掌握并能熟练运用数量积的运算律;
掌握模长公式.1、向量的数量积的定义已知两个非零向量 与 ,它们的夹
角为θ, 我们把数量 叫做
与 的数量积(或内积,点乘),即 注: 1、两向量的数量积是一个数量,而不是向量,符号由夹角决定2、 a · b不能写成a×b ,符号“·”在向量运算中不是乘号,不能省略.展示汇报 反馈点拨 例1、应用举例 问题 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?2.向量数量积的几何意义(1)给出向量投影的概念(2)问题6:数量积的几何意义是什么?O2、向量数量积的几何意义注:数量积的性质平面向量数量积的运算律 我们学过了实数乘法的哪些运算律?这些运算律对向量是否也适用? 经验证,数量积满足如下运算律(交换律)(数乘结合律)(分配律)4、数量积运算律说明:常用公式课本105页例2巩固训练 拓展提升例若 , ,且 , 则是多少?变式一:变式二:在△ABC中, 求,课堂小结:1、向量的数量积的定义2、向量数量积的几何意义课堂小结3、向量数量积的性质4、数量积运算律课堂小结:(交换律)(数乘结合律)(分配律)作业: 课本P108习题2.4A组1、2、3。
