人教版 数学 必修3 3.1.3 概率的基本性(16张PPT)
文档属性
| 名称 | 人教版 数学 必修3 3.1.3 概率的基本性(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-29 07:29:31 | ||
图片预览




文档简介
课件16张PPT。3.1.3
概率的基本性质
事件的关系
与运算
概率的基
本性质
思考:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果? 在掷骰子的试验中,我们可以定义许多事件,如:
C1 ={ 出现 1 点 };C2 ={出现 2 点};C3 ={ 出现 3 点 };
C4 ={ 出现 4 点 };C5 ={出现 5 点};C6 ={ 出现 6 点 };思考:1. 上述事件中有必然事件或不可能事件吗?5. 在掷骰子实验中事件G和事件H是否一定有一个会发生?4. 若只掷一次骰子,则事件C1和事件C2有可能同时发生么?3.上述事件中,哪些事件发生当且仅当事件D2且事件D3同时发生?2. 若事件C1发生,则还有哪些事件也一定会发生?探究反过来可以么?D1 ={ 出现的点数不大于 1 }; D2 ={ 出现的点数大于 3 };
D3 ={ 出现的点数小于 5 };
E ={ 出现的点数小于 7 }; F ={ 出现的点数大于 6 };
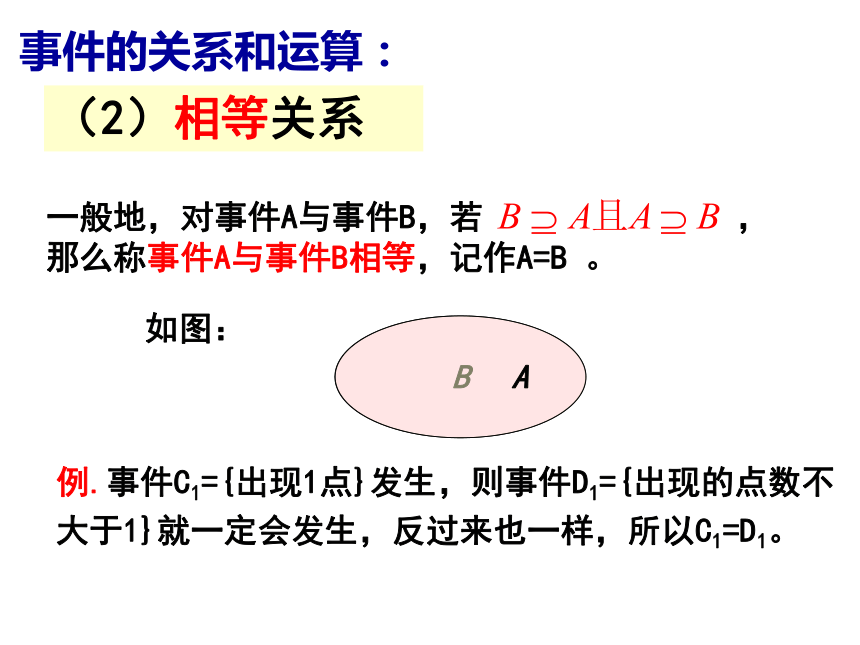
G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 };……你能写出这个试验中出现的其它一些事件吗?一、事件的关系和运算:BA如图:例.事件C1 ={出现1点 }发生,则事件 H ={出现的点数为奇数}也一定会发生,所以注:不可能事件记作 ,任何事件都包括不可能事件。(1)包含关系一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B),记作(2)相等关系B A如图:例.事件C1={出现1点}发生,则事件D1={出现的点数不大于1}就一定会发生,反过来也一样,所以C1=D1。事件的关系和运算:一般地,对事件A与事件B,若 ,那么称事件A与事件B相等,记作A=B 。(3)并事件(和事件)若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A和事件B的并事件(或和事件),记作 。B A如图:例.若事件K={出现1点或5点} 发生,则事件C1 =
{出现1点}与事件C5 ={出现 5 点 }中至少有一个会
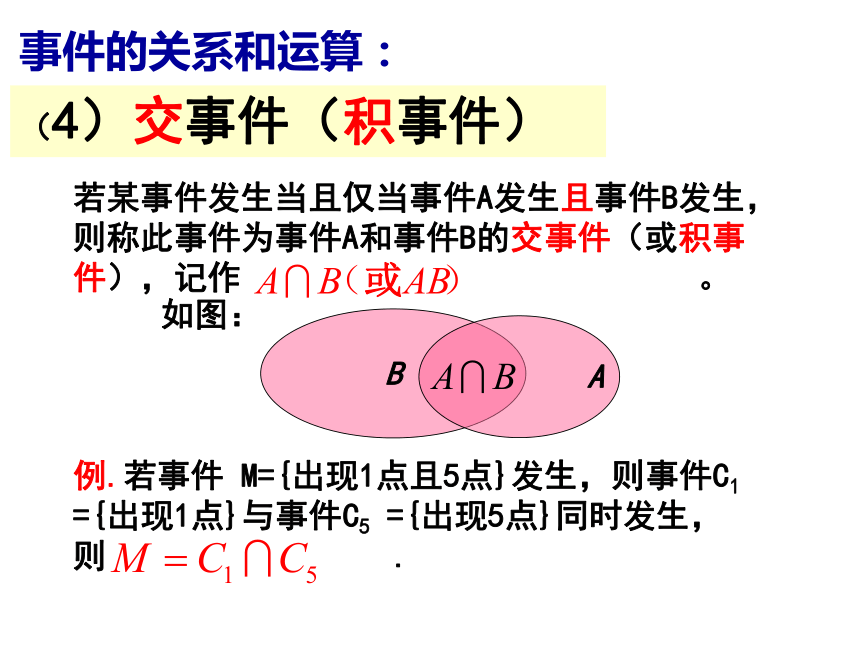
发生,则K .事件的关系和运算:(4)交事件(积事件)若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A和事件B的交事件(或积事件),记作 。B A如图:事件的关系和运算:例.若事件 M={出现1点且5点}发生,则事件C1 ={出现1点}与事件C5 ={出现5点}同时发生,则 .(5)互斥事件若 为不可能事件( ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中都不会同时发生。AB如图:例.因为事件C1={出现1点}与事件C2={出现2点}不可能
同时发生,故这两个事件互斥。事件的关系和运算:(6)互为对立事件若 为不可能事件, 为必然事件,那么称事件A与事件B互为对立事件,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生。如图:例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数} 即为互为对立事件。事件的关系和运算:互斥事件与对立事件的区别与联系 对立事件除了要求这两个事件不同时发生之外,要求二者之一必须有一个发生相同点:互斥事件和对立事件都不会同时发生不同点:互斥中的两个事件可能都不发生联系:对立事件是互斥事件,而互斥事件未必是对立事件,对立事件是互斥事件的特殊情形
例题分析:
例1 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;
事件B:命中环数为10环;
事件C:命中环数小于6环;
事件D:命中环数为6、7、8、9、10环.解:互斥事件有:A和C、B和C、C和D.
对立事件有:C和D.二.概率的基本性质:(1)任何事件的概率在0~1之间,即0≤P(A)≤1(2)必然事件的概率为1,即P(A)=1(3)不可能事件的概率为0,即P(A)=0思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频数
与事件C1和事件C3发生的频数之间有什
么关系?结论:当事件A与事件B互斥时
(4)概率的加法公式
如果事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)(5)如果事件B与事件A是互为对立事件,则
P(B)=1-P(A)事件G与事件H互为对立事件,则 为必然事件,例2 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是0.25,取到方块(事件B)的概率是0.25,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?解:(1)P(C)=P(A)+ P(B)=0.25+0.25=0.5;
(2)P(D)=1-P(C)=1-0.5=0.5.概率的基本性质事件的关系与运算包含关系概率的基本性质相等关系并(和)事件交(积)事件互斥事件对立事件必然事件的概率为1不可能事件的概率为0概率的加法公式对立事件计算公式0≤P(A) ≤1
概率的基本性质
事件的关系
与运算
概率的基
本性质
思考:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果? 在掷骰子的试验中,我们可以定义许多事件,如:
C1 ={ 出现 1 点 };C2 ={出现 2 点};C3 ={ 出现 3 点 };
C4 ={ 出现 4 点 };C5 ={出现 5 点};C6 ={ 出现 6 点 };思考:1. 上述事件中有必然事件或不可能事件吗?5. 在掷骰子实验中事件G和事件H是否一定有一个会发生?4. 若只掷一次骰子,则事件C1和事件C2有可能同时发生么?3.上述事件中,哪些事件发生当且仅当事件D2且事件D3同时发生?2. 若事件C1发生,则还有哪些事件也一定会发生?探究反过来可以么?D1 ={ 出现的点数不大于 1 }; D2 ={ 出现的点数大于 3 };
D3 ={ 出现的点数小于 5 };
E ={ 出现的点数小于 7 }; F ={ 出现的点数大于 6 };
G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 };……你能写出这个试验中出现的其它一些事件吗?一、事件的关系和运算:BA如图:例.事件C1 ={出现1点 }发生,则事件 H ={出现的点数为奇数}也一定会发生,所以注:不可能事件记作 ,任何事件都包括不可能事件。(1)包含关系一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B),记作(2)相等关系B A如图:例.事件C1={出现1点}发生,则事件D1={出现的点数不大于1}就一定会发生,反过来也一样,所以C1=D1。事件的关系和运算:一般地,对事件A与事件B,若 ,那么称事件A与事件B相等,记作A=B 。(3)并事件(和事件)若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A和事件B的并事件(或和事件),记作 。B A如图:例.若事件K={出现1点或5点} 发生,则事件C1 =
{出现1点}与事件C5 ={出现 5 点 }中至少有一个会
发生,则K .事件的关系和运算:(4)交事件(积事件)若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A和事件B的交事件(或积事件),记作 。B A如图:事件的关系和运算:例.若事件 M={出现1点且5点}发生,则事件C1 ={出现1点}与事件C5 ={出现5点}同时发生,则 .(5)互斥事件若 为不可能事件( ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中都不会同时发生。AB如图:例.因为事件C1={出现1点}与事件C2={出现2点}不可能
同时发生,故这两个事件互斥。事件的关系和运算:(6)互为对立事件若 为不可能事件, 为必然事件,那么称事件A与事件B互为对立事件,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生。如图:例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数} 即为互为对立事件。事件的关系和运算:互斥事件与对立事件的区别与联系 对立事件除了要求这两个事件不同时发生之外,要求二者之一必须有一个发生相同点:互斥事件和对立事件都不会同时发生不同点:互斥中的两个事件可能都不发生联系:对立事件是互斥事件,而互斥事件未必是对立事件,对立事件是互斥事件的特殊情形
例题分析:
例1 一个射手进行一次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;
事件B:命中环数为10环;
事件C:命中环数小于6环;
事件D:命中环数为6、7、8、9、10环.解:互斥事件有:A和C、B和C、C和D.
对立事件有:C和D.二.概率的基本性质:(1)任何事件的概率在0~1之间,即0≤P(A)≤1(2)必然事件的概率为1,即P(A)=1(3)不可能事件的概率为0,即P(A)=0思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频数
与事件C1和事件C3发生的频数之间有什
么关系?结论:当事件A与事件B互斥时
(4)概率的加法公式
如果事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)(5)如果事件B与事件A是互为对立事件,则
P(B)=1-P(A)事件G与事件H互为对立事件,则 为必然事件,例2 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是0.25,取到方块(事件B)的概率是0.25,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?解:(1)P(C)=P(A)+ P(B)=0.25+0.25=0.5;
(2)P(D)=1-P(C)=1-0.5=0.5.概率的基本性质事件的关系与运算包含关系概率的基本性质相等关系并(和)事件交(积)事件互斥事件对立事件必然事件的概率为1不可能事件的概率为0概率的加法公式对立事件计算公式0≤P(A) ≤1
