陕西省榆林市第二中学2018-2019学年高一下学期第二次月考数学试题
文档属性
| 名称 | 陕西省榆林市第二中学2018-2019学年高一下学期第二次月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-30 00:00:00 | ||
图片预览



文档简介
榆林市第二中学2018--2019学年第二学期第二次月考
高一年级数学试题
命题人:
时间:120分钟 满分:150分
一、选择题(本大题共12小题,共60分)
向量,=(-1,2),则=( )
A. 6 B. 5 C. 1 D.
直线,直线?的方向向量为,且,则
A. B. C. 2 D.
把函数y=sin(2x+)图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将图象向右平移个单位,得到函数y=g(x),那么g()的值为( )
A. B. C. D.
设非零向量,满足则(? ? ? ? )
A. B. C. ? D.
已知平面向量是非零向量,,,则向量在向量方向上的投影为? ?
A. 1 B. C. 2 D.
如图,在△ABC中,,,若,则λ+μ的值为( )
A. B. C. D.
已知向量,向量,则△ABC的形状为( )
A. 等腰直角三角形 B. 等边三角形 C. 直角非等腰三角形 D. 等腰非直角三角形
已知两点,,则与向量共线的单位向量是 .
A. B. , C. D. ,
函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,若其图象向左平移个单位后得到的函数为奇函数,则函数f(x)的图象( )
A. 关于点对称 B. 关于点对称 C. 关于直线对称 D. 关于直线对称
已知是单位向量,的夹角为,若向量,则的最大值为
A. B. C. 2 D.
已知ABCD的三个顶点A(-1,-2),B(3,1),C(0,2),则顶点D的坐标为( )
A. B. C. D.
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
A. 2 B. C. D.
二、填空题(本大题共4小题,共20分)
设,是不共线向量,与共线,则实数k为______ .
设x∈R,向量,,且⊥,则= ______ .
已知函数,的最大值为4,则正实数a的值为______ .
一条河宽为,一船从出发航行垂直到达河正对岸的处,船速为.水速为,则船到达处所需时间为 ________________.
三、解答题(本大题共6小题,共70分)
(本题10分)已知向量=(-3,1),=(1,-2),=+k(k∈R). (1)若与向量2-垂直,求实数k的值; (2)若向量=(1,-1),且与向量k+平行,求实数k的值.
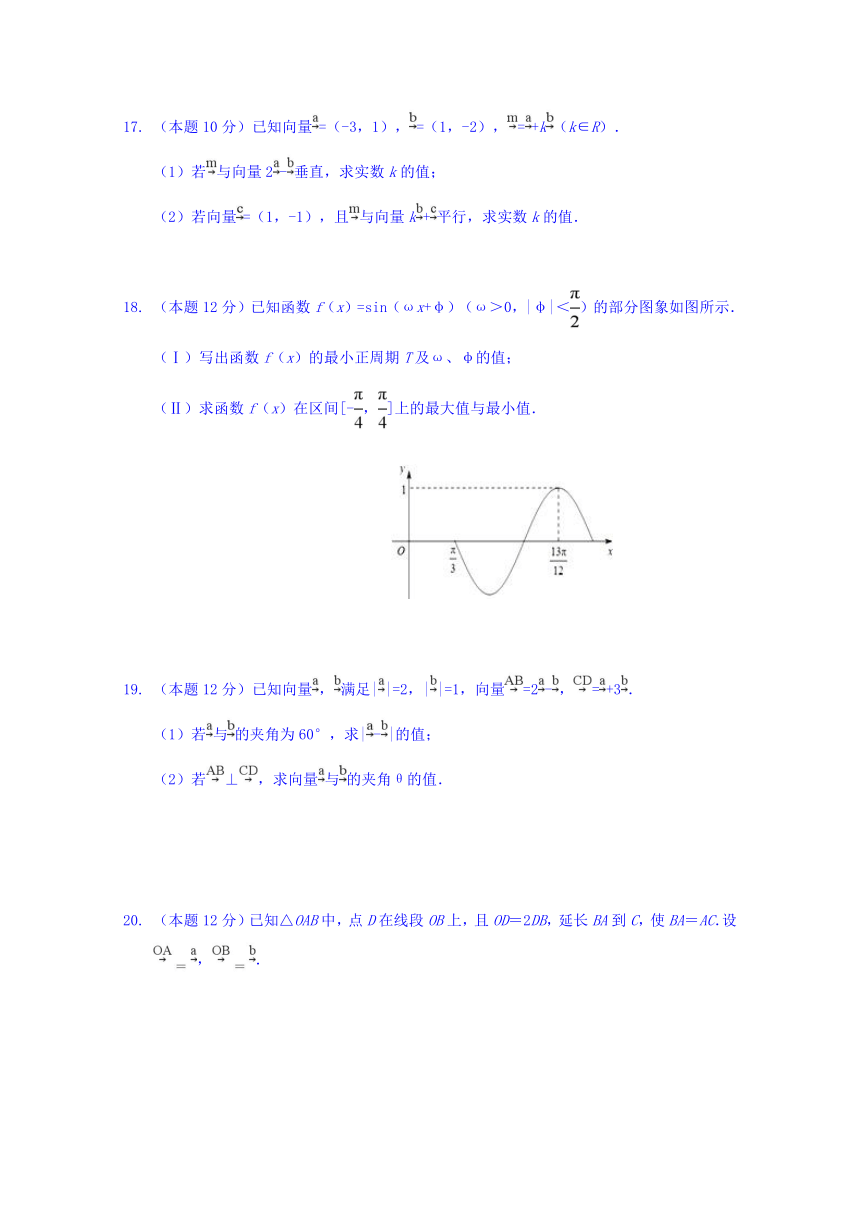
(本题12分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示. (Ⅰ)写出函数f(x)的最小正周期T及ω、φ的值; (Ⅱ)求函数f(x)在区间[-,]上的最大值与最小值.
(本题12分)已知向量,满足||=2,||=1,向量=2-,=+3. (1)若与的夹角为60°,求|-|的值; (2)若⊥,求向量与的夹角θ的值.
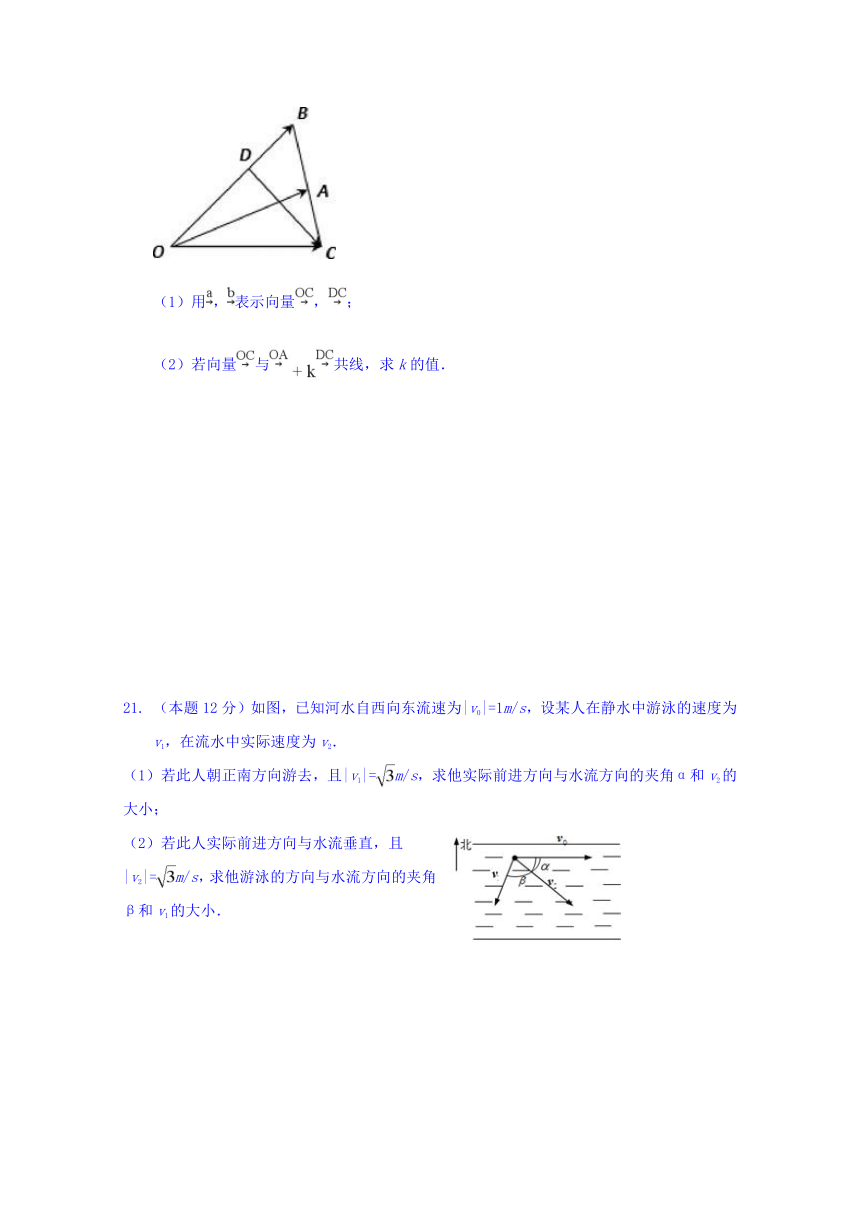
(本题12分)已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设,.
(1)用,表示向量,;
(2)若向量与共线,求k的值.
(本题12分)如图,已知河水自西向东流速为|v0|=1m/s,设某人在静水中游泳的速度为v1,在流水中实际速度为v2.
若此人朝正南方向游去,且|v1|=m/s,求他实际前进方向与水流方向的夹角α和v2的大小; (2)若此人实际前进方向与水流垂直,且|v2|=m/s,求他游泳的方向与水流方向的夹角β和v1的大小.
(本题12分)已知函数的?部分图象如图所示: (1)求f(x)的解析式; (2)求f(x)的单调区间和对称中心坐标; (3)将f(x)的图象向左平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在上的最大值和最小值.
高一数学月考答案
1.A 2.B 3.B 4.A 5.B 6.A 7.A 8.D 9.C 10.D 11.D 12. C
13. ? 14. 5 15. 2 16. 1.5
17.解:(1)=+k=(-3+k,1-2k),2-=(-7,4). ∵与向量2-垂直,∴?(2-)=-7(-3+k)+4(1-2k)=0,解得k=. (2)k+=(k+1,-2k-1),∵与向量k+平行, ∴(-2k-1)(-3+k)-(1-2k)(k+1)=0,解得k=.
18.解:(Ⅰ)根据函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象,
可得=-,求得ω=2, ?∴最小正周期T==π. 再根据五点法作图可得2?+φ=π, ?求得φ=; (Ⅱ)由以上可得,f(x)=sin(2x+),在区间[-,]上,
2x+∈[-,],sin(2x+)∈[-,1], 当2x+=-时,即x=-,函数f(x)取得最小值为-. 当2x+=时,即x=,函数f(x)取得最大值为1.
19.解:(1)=2×1×cos60°=1. ∴|-|2=2-2+2=3. ∴|-|=. (2)∵⊥,∴?=0, 即(2-)?(+3)=22+5-32=8+10cosθ-3=0. ∴cosθ=,又 ?∴θ=120°.
20.解:(1)∵A为BC的中点,∴, 可得, 而 (2)由(1),得, ∵与共线,设 即, 根据平面向量基本定理,得 解之得,.
21.解:如图,设=v0,=,=, 则由题意知=+,||=1, 根据向量加法的平行四边形法则得四边形OACB为平行四边形. (1)由此人朝正南方向游去得四边形OACB为矩形,且||=AC=,如下图所示, 则在直角△OAC中,||=OC==2, tan∠AOC==,又α=∠AOC∈(0,),所以α=; (2)由题意知α=∠OCB=,且||=|OC|=,BC=1,如下图所示, 则在直角△OBC中,||=OB==2, tan∠BOC==, 又∠AOC∈(0,),所以∠BOC=, 则β==, 答:(1)他实际前进方向与水流方向的夹角α为,v2的大小为2m/s; (2)他游泳的方向与水流方向的夹角β为,v1的大小为2m/s.
22.解:(1)由图象可知, 解得, 又由于, 所以, 由图象及五点法作图可知:, 所以, 所以; (2)由(1)知,, 令,得, 所以f(x)的单调递增区间为, 令,得, 所以f(x)的单调递减区间为, 令,得, 所以f(x)的对称中心的坐标为; (3)由已知的图象变换过程可得:, 因为, 所以, 所以当,得时,g(x)取得最小值, 当时,即x=0时,g(x)取得最大值.
高一年级数学试题
命题人:
时间:120分钟 满分:150分
一、选择题(本大题共12小题,共60分)
向量,=(-1,2),则=( )
A. 6 B. 5 C. 1 D.
直线,直线?的方向向量为,且,则
A. B. C. 2 D.
把函数y=sin(2x+)图象上各点的横坐标缩短到原来的倍(纵坐标不变),再将图象向右平移个单位,得到函数y=g(x),那么g()的值为( )
A. B. C. D.
设非零向量,满足则(? ? ? ? )
A. B. C. ? D.
已知平面向量是非零向量,,,则向量在向量方向上的投影为? ?
A. 1 B. C. 2 D.
如图,在△ABC中,,,若,则λ+μ的值为( )
A. B. C. D.
已知向量,向量,则△ABC的形状为( )
A. 等腰直角三角形 B. 等边三角形 C. 直角非等腰三角形 D. 等腰非直角三角形
已知两点,,则与向量共线的单位向量是 .
A. B. , C. D. ,
函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,若其图象向左平移个单位后得到的函数为奇函数,则函数f(x)的图象( )
A. 关于点对称 B. 关于点对称 C. 关于直线对称 D. 关于直线对称
已知是单位向量,的夹角为,若向量,则的最大值为
A. B. C. 2 D.
已知ABCD的三个顶点A(-1,-2),B(3,1),C(0,2),则顶点D的坐标为( )
A. B. C. D.
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
A. 2 B. C. D.
二、填空题(本大题共4小题,共20分)
设,是不共线向量,与共线,则实数k为______ .
设x∈R,向量,,且⊥,则= ______ .
已知函数,的最大值为4,则正实数a的值为______ .
一条河宽为,一船从出发航行垂直到达河正对岸的处,船速为.水速为,则船到达处所需时间为 ________________.
三、解答题(本大题共6小题,共70分)
(本题10分)已知向量=(-3,1),=(1,-2),=+k(k∈R). (1)若与向量2-垂直,求实数k的值; (2)若向量=(1,-1),且与向量k+平行,求实数k的值.
(本题12分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示. (Ⅰ)写出函数f(x)的最小正周期T及ω、φ的值; (Ⅱ)求函数f(x)在区间[-,]上的最大值与最小值.
(本题12分)已知向量,满足||=2,||=1,向量=2-,=+3. (1)若与的夹角为60°,求|-|的值; (2)若⊥,求向量与的夹角θ的值.
(本题12分)已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设,.
(1)用,表示向量,;
(2)若向量与共线,求k的值.
(本题12分)如图,已知河水自西向东流速为|v0|=1m/s,设某人在静水中游泳的速度为v1,在流水中实际速度为v2.
若此人朝正南方向游去,且|v1|=m/s,求他实际前进方向与水流方向的夹角α和v2的大小; (2)若此人实际前进方向与水流垂直,且|v2|=m/s,求他游泳的方向与水流方向的夹角β和v1的大小.
(本题12分)已知函数的?部分图象如图所示: (1)求f(x)的解析式; (2)求f(x)的单调区间和对称中心坐标; (3)将f(x)的图象向左平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在上的最大值和最小值.
高一数学月考答案
1.A 2.B 3.B 4.A 5.B 6.A 7.A 8.D 9.C 10.D 11.D 12. C
13. ? 14. 5 15. 2 16. 1.5
17.解:(1)=+k=(-3+k,1-2k),2-=(-7,4). ∵与向量2-垂直,∴?(2-)=-7(-3+k)+4(1-2k)=0,解得k=. (2)k+=(k+1,-2k-1),∵与向量k+平行, ∴(-2k-1)(-3+k)-(1-2k)(k+1)=0,解得k=.
18.解:(Ⅰ)根据函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象,
可得=-,求得ω=2, ?∴最小正周期T==π. 再根据五点法作图可得2?+φ=π, ?求得φ=; (Ⅱ)由以上可得,f(x)=sin(2x+),在区间[-,]上,
2x+∈[-,],sin(2x+)∈[-,1], 当2x+=-时,即x=-,函数f(x)取得最小值为-. 当2x+=时,即x=,函数f(x)取得最大值为1.
19.解:(1)=2×1×cos60°=1. ∴|-|2=2-2+2=3. ∴|-|=. (2)∵⊥,∴?=0, 即(2-)?(+3)=22+5-32=8+10cosθ-3=0. ∴cosθ=,又 ?∴θ=120°.
20.解:(1)∵A为BC的中点,∴, 可得, 而 (2)由(1),得, ∵与共线,设 即, 根据平面向量基本定理,得 解之得,.
21.解:如图,设=v0,=,=, 则由题意知=+,||=1, 根据向量加法的平行四边形法则得四边形OACB为平行四边形. (1)由此人朝正南方向游去得四边形OACB为矩形,且||=AC=,如下图所示, 则在直角△OAC中,||=OC==2, tan∠AOC==,又α=∠AOC∈(0,),所以α=; (2)由题意知α=∠OCB=,且||=|OC|=,BC=1,如下图所示, 则在直角△OBC中,||=OB==2, tan∠BOC==, 又∠AOC∈(0,),所以∠BOC=, 则β==, 答:(1)他实际前进方向与水流方向的夹角α为,v2的大小为2m/s; (2)他游泳的方向与水流方向的夹角β为,v1的大小为2m/s.
22.解:(1)由图象可知, 解得, 又由于, 所以, 由图象及五点法作图可知:, 所以, 所以; (2)由(1)知,, 令,得, 所以f(x)的单调递增区间为, 令,得, 所以f(x)的单调递减区间为, 令,得, 所以f(x)的对称中心的坐标为; (3)由已知的图象变换过程可得:, 因为, 所以, 所以当,得时,g(x)取得最小值, 当时,即x=0时,g(x)取得最大值.
同课章节目录
