人教版九年级上册24.4 弧长及扇形的面积课件(20张PPT)
文档属性
| 名称 | 人教版九年级上册24.4 弧长及扇形的面积课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 553.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-01 08:35:51 | ||
图片预览


文档简介
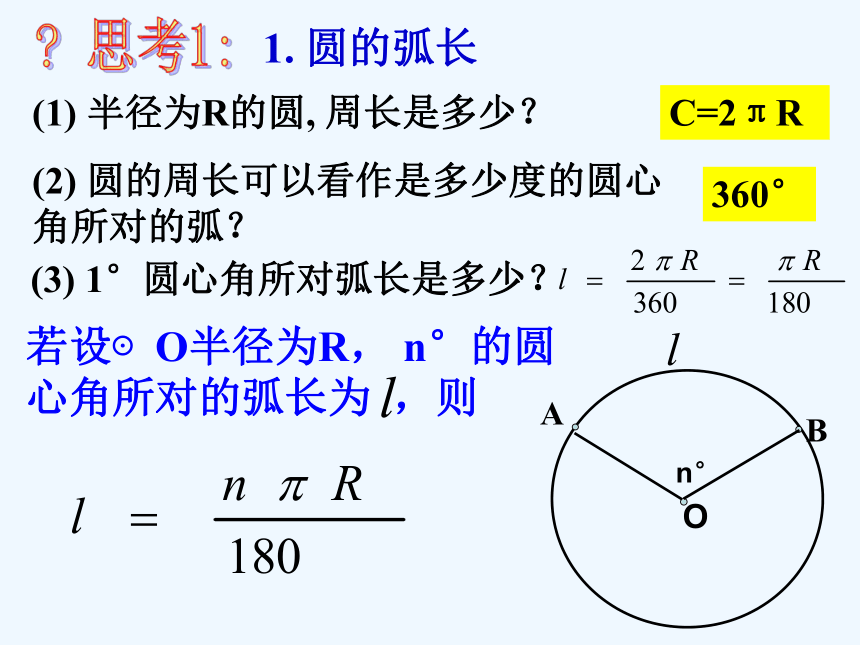
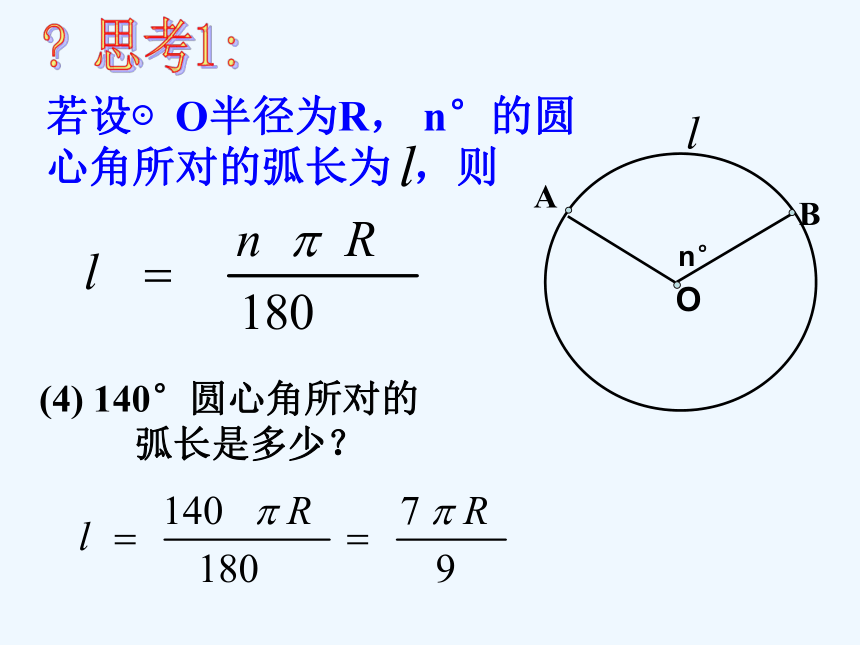
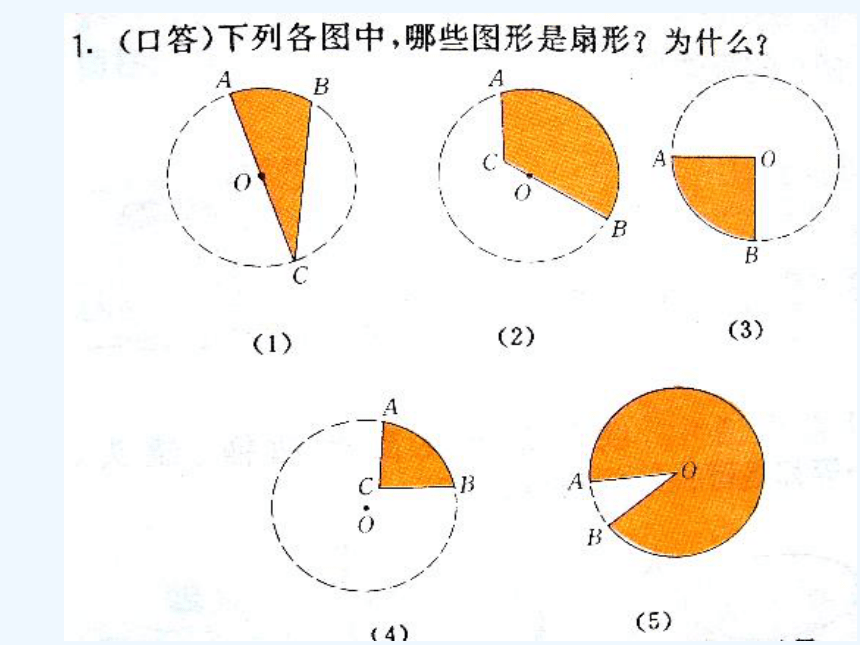
课件20张PPT。24.4 弧长和扇形面积(1)C=2πR (3) 1°圆心角所对弧长是多少? (2) 圆的周长可以看作是多少度的圆心角所对的弧?(1) 半径为R的圆, 周长是多少?? 思考1:360°1. 圆的弧长n°ABO? 思考1:(4) 140°圆心角所对的
弧长是多少? 1. 已知弧所对的圆心角为900,半径是4,则弧长为______.
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为______.
3. 钟表的轴心到分针针端的长为5cm, 那么经过40分钟,分针针端转过的弧长是 ( )
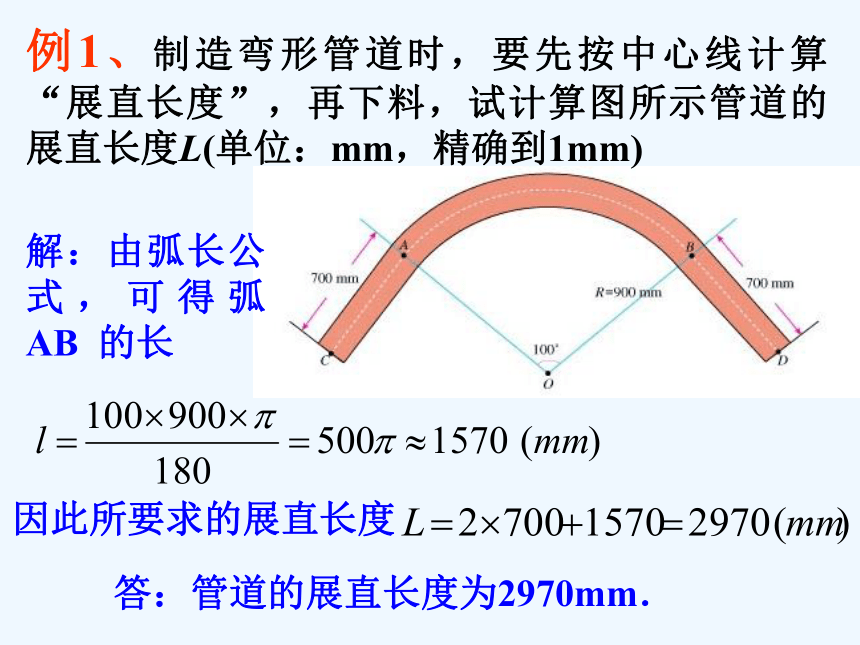
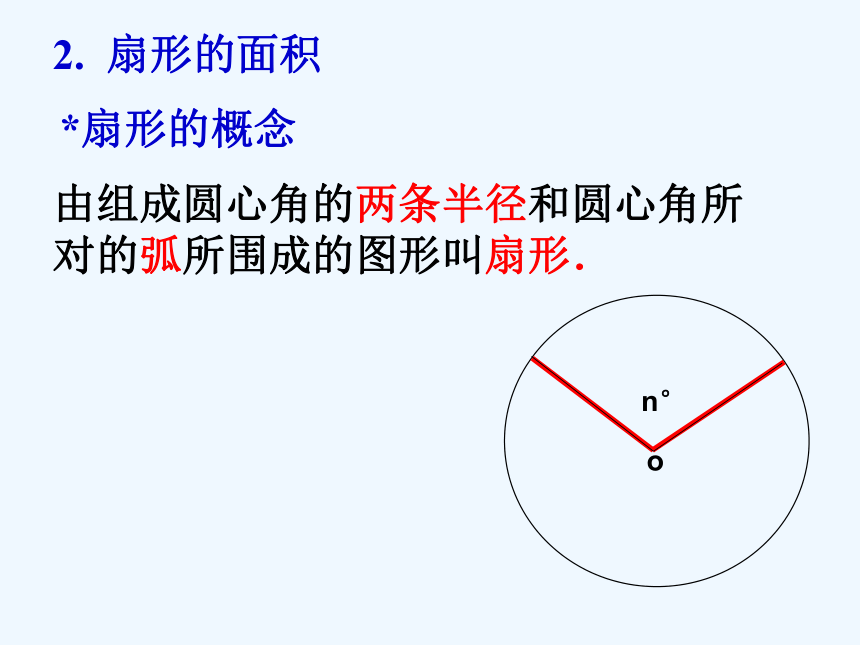
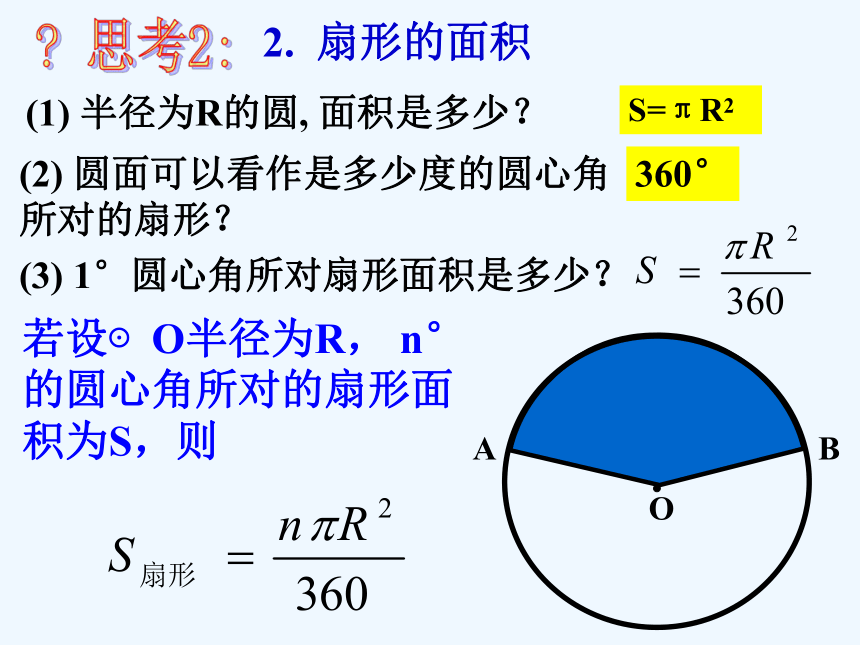
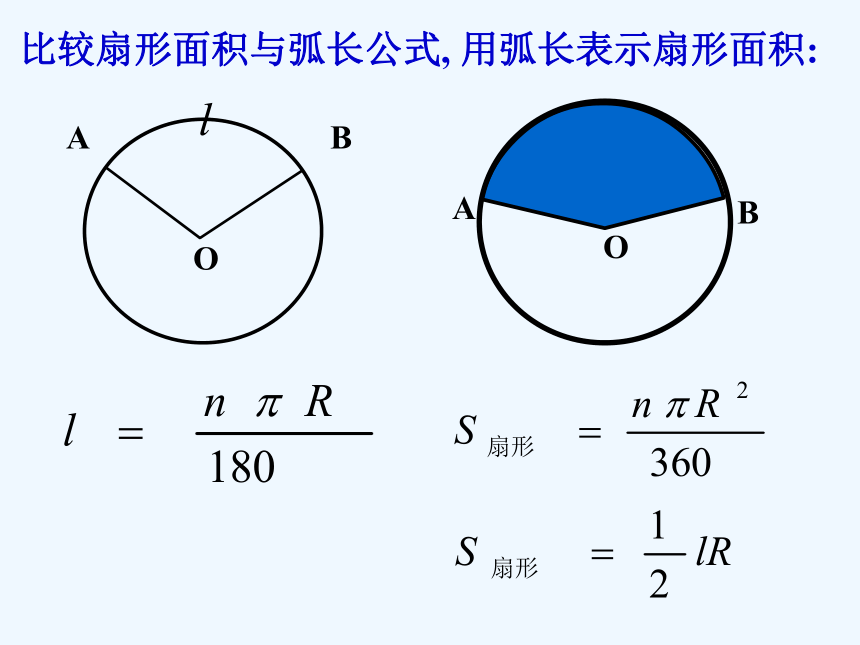
A. B. C. D. 练习12π160°B例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)解:由弧长公式,可得弧AB 的长因此所要求的展直长度 答:管道的展直长度为2970mm. 由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形.n°o2. 扇形的面积*扇形的概念O(1) 半径为R的圆, 面积是多少?S=πR2(3) 1°圆心角所对扇形面积是多少? (2) 圆面可以看作是多少度的圆心角所对的扇形?若设⊙O半径为R, n°的圆心角所对的扇形面 积为S,则 ? 思考2:2. 扇形的面积360°比较扇形面积与弧长公式, 用弧长表示扇形面积:AB1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形= .练习2 3、已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积是_______.A. B. C. D. 4、如图,这是中央电视台“曲苑杂谈”中的一 副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为 ( )B练习2例2:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。 (精确到0.01m)CD3. 弓形面积由弦及其所对的弧组成的图形叫做弓形. 弓形:弓形面积:弓形面积可以由扇形和三角形的面积来计算.弓形面积:ABDCE有水部分的面积
= S扇+ S△练习3分析:0.60.30.3 2. 如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1, 顺次连接四个圆心得到四边形ABCD, 则图形中四个扇形(空白部分)的面积之和是______.π 3. 如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为______个平方单位.πn°ABO设⊙O半径为R, n°的圆心角所对的扇形面积 为S,则 2. 扇形的面积1. 圆的弧长小结3. 弓形面积
弧长是多少? 1. 已知弧所对的圆心角为900,半径是4,则弧长为______.
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为______.
3. 钟表的轴心到分针针端的长为5cm, 那么经过40分钟,分针针端转过的弧长是 ( )
A. B. C. D. 练习12π160°B例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)解:由弧长公式,可得弧AB 的长因此所要求的展直长度 答:管道的展直长度为2970mm. 由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形.n°o2. 扇形的面积*扇形的概念O(1) 半径为R的圆, 面积是多少?S=πR2(3) 1°圆心角所对扇形面积是多少? (2) 圆面可以看作是多少度的圆心角所对的扇形?若设⊙O半径为R, n°的圆心角所对的扇形面 积为S,则 ? 思考2:2. 扇形的面积360°比较扇形面积与弧长公式, 用弧长表示扇形面积:AB1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形= .练习2 3、已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积是_______.A. B. C. D. 4、如图,这是中央电视台“曲苑杂谈”中的一 副图案,它是一扇形图形,其中∠AOB为1200,OC长为8cm,CA长为12cm,则贴纸部分的面积为 ( )B练习2例2:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。 (精确到0.01m)CD3. 弓形面积由弦及其所对的弧组成的图形叫做弓形. 弓形:弓形面积:弓形面积可以由扇形和三角形的面积来计算.弓形面积:ABDCE有水部分的面积
= S扇+ S△练习3分析:0.60.30.3 2. 如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1, 顺次连接四个圆心得到四边形ABCD, 则图形中四个扇形(空白部分)的面积之和是______.π 3. 如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为______个平方单位.πn°ABO设⊙O半径为R, n°的圆心角所对的扇形面积 为S,则 2. 扇形的面积1. 圆的弧长小结3. 弓形面积
同课章节目录
