第一章 丰富的图形世界 2 展开与折叠 第2课时 柱体、锥体的展开与折叠(学案)
文档属性
| 名称 | 第一章 丰富的图形世界 2 展开与折叠 第2课时 柱体、锥体的展开与折叠(学案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-03 10:40:52 | ||
图片预览


文档简介
第一章 丰富的图形世界
2 展开与折叠
第2课时 柱体、锥体的展开与折叠
自主预习
1.棱柱的表面展开图是由两个形状相同的多边形和一些________形组成的.沿棱柱表面不同的棱剪开,可得到不同的组合方式的表面展开图.
2.圆柱的表面展开图是两个________和一个长方形.
3.圆锥的表面展开图是一个圆和一个_________形.
4.棱锥的表面展开图有一个是多边形,其余都是_________形.
课堂巩固
知识点:柱体、锥体的展开与折叠
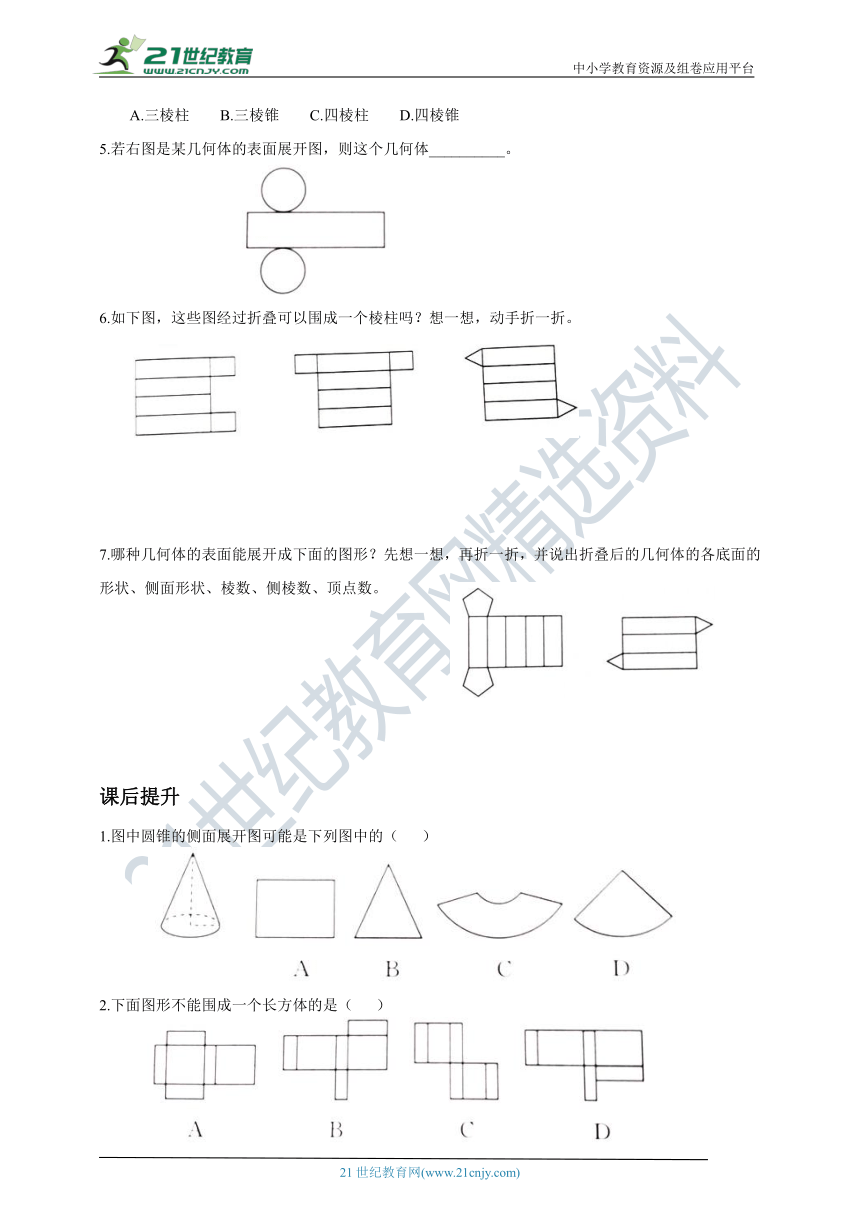
1.下列立体图形中,侧面展开图是扇形的是( )
2.如图,圆柱体的表面展开后得到的平面图形是( )
3.下列四个图形中,是三棱锥的展开图的是( )
4.一个几何体的展开图如图所示,这个几何体是( )
A.三棱柱 B.三棱锥 C.四棱柱 D.四棱锥
5.若右图是某几何体的表面展开图,则这个几何体__________。
6.如下图,这些图经过折叠可以围成一个棱柱吗?想一想,动手折一折。
7.哪种几何体的表面能展开成下面的图形?先想一想,再折一折,并说出折叠后的几何体的各底面的形状、侧面形状、棱数、侧棱数、顶点数。
课后提升
1.图中圆锥的侧面展开图可能是下列图中的( )
2.下面图形不能围成一个长方体的是( )
3.下面图形经过折叠不能围成棱柱的是( )
4.一个几何体的表面展开图如图所示,则这个几何体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
5.将图①中的正四棱锥 ABCDE沿着其中的四个边剪开后,形成的展开图为图②,判断下列哪一个选项中的四个边可为剪开四个边?
A.AC,AD,BC,DE B .AB,BE,DE,CD
C. AC,BC,AE,DE D.AC,AD,AE,BC
6.某个立体图形的平面展开图如图所示,那么这个几何体是________。
7.一个正棱柱(底面为正多边形),有30条棱,侧棱长为10 cm,底面边长为1 cm.
(1)这是几棱柱?
(2)此棱柱的侧面积是多少?
8.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果A面在长方体的底部,那么哪一个面会在上面?
(2)如果F面在前面,B面在左面,那么哪一个面会在上面?(字母朝外)
(3)如果C面在右面,D面在后面,那么哪一个面会在上面?(字母朝外)
创新探究
9.如图是一张铁皮.
(1)计算该铁皮的面积.
(2)能否用它做成了一个长方体盒子?若能,画出这个长方体盒子,并计算该长方体盒子的体积;若不能,请说明理由。
参考答案及解析
自主预习
1.长方 2.圆 3.扇 4.三角
课堂巩固
1.B 2.B 3.B 4.C 5.圆柱
6.中间一个可以围成一个棱柱。
7.解:左边的图形是(正)五棱柱:底面是正五边形,侧面是长方形,有15条棱,5条侧棱,10个顶点右边的图形是(正三棱柱:底面是三角形,侧面是长方形,有9条棱,3条侧棱,6个顶点。
课后提升
1.D 2.D 3.D 4.A 5.A 6.三棱柱
7.解:(1)30÷3=10,这是十棱柱,
(2)10×1×10=100(cm2),即此棱柱的侧面积是100cm2。
8.解:(1)因为面“A”与面“F”相对,所以A面是长方体的底部时,F面在上面;
(2)由题图可知,如果F面在前面,B面在左面,那么“E”面在下面,因为面“C”与面“E”相对,所以C面会在上面;(3)由题图可知,如果C面在右面,D面在后面,那么“F”面在下面,因为面“A”与面“F”相对,所以A面在上面。
创新探究
9.解:(1)该铁皮的面积为(1×3)×2+(2×3)×2+(1×2)×2=22(dm2).
(2)能做成一个长方体盒子.如图所示,该长方体盒子的体积为3×1×2=6(dm3)。
2 展开与折叠
第2课时 柱体、锥体的展开与折叠
自主预习
1.棱柱的表面展开图是由两个形状相同的多边形和一些________形组成的.沿棱柱表面不同的棱剪开,可得到不同的组合方式的表面展开图.
2.圆柱的表面展开图是两个________和一个长方形.
3.圆锥的表面展开图是一个圆和一个_________形.
4.棱锥的表面展开图有一个是多边形,其余都是_________形.
课堂巩固
知识点:柱体、锥体的展开与折叠
1.下列立体图形中,侧面展开图是扇形的是( )
2.如图,圆柱体的表面展开后得到的平面图形是( )
3.下列四个图形中,是三棱锥的展开图的是( )
4.一个几何体的展开图如图所示,这个几何体是( )
A.三棱柱 B.三棱锥 C.四棱柱 D.四棱锥
5.若右图是某几何体的表面展开图,则这个几何体__________。
6.如下图,这些图经过折叠可以围成一个棱柱吗?想一想,动手折一折。
7.哪种几何体的表面能展开成下面的图形?先想一想,再折一折,并说出折叠后的几何体的各底面的形状、侧面形状、棱数、侧棱数、顶点数。
课后提升
1.图中圆锥的侧面展开图可能是下列图中的( )
2.下面图形不能围成一个长方体的是( )
3.下面图形经过折叠不能围成棱柱的是( )
4.一个几何体的表面展开图如图所示,则这个几何体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
5.将图①中的正四棱锥 ABCDE沿着其中的四个边剪开后,形成的展开图为图②,判断下列哪一个选项中的四个边可为剪开四个边?
A.AC,AD,BC,DE B .AB,BE,DE,CD
C. AC,BC,AE,DE D.AC,AD,AE,BC
6.某个立体图形的平面展开图如图所示,那么这个几何体是________。
7.一个正棱柱(底面为正多边形),有30条棱,侧棱长为10 cm,底面边长为1 cm.
(1)这是几棱柱?
(2)此棱柱的侧面积是多少?
8.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果A面在长方体的底部,那么哪一个面会在上面?
(2)如果F面在前面,B面在左面,那么哪一个面会在上面?(字母朝外)
(3)如果C面在右面,D面在后面,那么哪一个面会在上面?(字母朝外)
创新探究
9.如图是一张铁皮.
(1)计算该铁皮的面积.
(2)能否用它做成了一个长方体盒子?若能,画出这个长方体盒子,并计算该长方体盒子的体积;若不能,请说明理由。
参考答案及解析
自主预习
1.长方 2.圆 3.扇 4.三角
课堂巩固
1.B 2.B 3.B 4.C 5.圆柱
6.中间一个可以围成一个棱柱。
7.解:左边的图形是(正)五棱柱:底面是正五边形,侧面是长方形,有15条棱,5条侧棱,10个顶点右边的图形是(正三棱柱:底面是三角形,侧面是长方形,有9条棱,3条侧棱,6个顶点。
课后提升
1.D 2.D 3.D 4.A 5.A 6.三棱柱
7.解:(1)30÷3=10,这是十棱柱,
(2)10×1×10=100(cm2),即此棱柱的侧面积是100cm2。
8.解:(1)因为面“A”与面“F”相对,所以A面是长方体的底部时,F面在上面;
(2)由题图可知,如果F面在前面,B面在左面,那么“E”面在下面,因为面“C”与面“E”相对,所以C面会在上面;(3)由题图可知,如果C面在右面,D面在后面,那么“F”面在下面,因为面“A”与面“F”相对,所以A面在上面。
创新探究
9.解:(1)该铁皮的面积为(1×3)×2+(2×3)×2+(1×2)×2=22(dm2).
(2)能做成一个长方体盒子.如图所示,该长方体盒子的体积为3×1×2=6(dm3)。
