高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):03【基础】空间几何体的三视图和直观图
文档属性
| 名称 | 高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):03【基础】空间几何体的三视图和直观图 |  | |
| 格式 | zip | ||
| 文件大小 | 363.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 08:24:39 | ||
图片预览




文档简介
空间几何体的三视图和直观图
【学习目标】
1.了解平行投影与中心投影,了解在平行投影下画空间图形与在中心投影下画空间图形两种方法的各自特点,了解空间图形的不同表现形式;
2. 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱的简易组合体)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测画法画出它们的直观图.
【要点梳理】
要点一、中心投影与平行投影
1.投影、投影线和投影面
由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做投影.其中的光线叫做投影线,留下物体影子的屏幕叫做投影面.
2.中心投影
我们把光由一点向外散射形成的投影叫做中心投影.中心投影的投影线交于一点,它的实质是一个点光源把一个物体射到一个平面上,这个物体的影子就是它在这个平面上的中心投影.
3.中心投影的性质
(1)中心投影的投影线交于一点;
(2)点光源距离物体越近,投影形成的影子越大.
4.平行投影
我们把在一束平行光线照射下形成的投影叫做平行投影.投影线正对着投影面时,叫做正投影,否则叫做斜投影.
5.平行投影的性质
(1)平行投影的投影线互相平行.
(2)在平行投影之下,与投影面平行的平面图形留下的影子与这个平面图形的形状和大小完全相同.
6.中心投影与平行投影的区别与联系
(1)平行投影包括斜二测画法和三视图.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.
(2)画实际效果图时,一般用中心投影法,画立体几何中的图形时,一般用平行投影法.
要点二、空间几何体的三视图
1.三视图的概念
把一个空间几何体投影到一个平面上,可以获得一个平面图形,但是只有一个平面图形很难把握几何体的全貌,因此我们需要从多个角度进行投影,这样才能较好地把握几何体的形状和大小.通常,我们总是选择三种投影.
(1)光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图;
(2)光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图;
(3)光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图.
几何体的正视图、侧视图和俯视图统称为几何体的三视图.
2.三视图的画法规则
画三视图时,以正视图为准,俯视图在正视图的正下方,侧视图在正视图的正右方,正、俯、侧三个视图之间必须互相对齐,不能错位.
正视图反映物体的长度和高度,俯视图反映物体的长度和宽度,侧视图反映物体的宽度和高度,由此,每两个视图之间有一定的对应关系,根据这种对应关系得到三视图的画法规则:
(1)正、俯视图都反映物体的长度——“长对正”;
(2)正、侧视图都反映物体的高度——“高平齐”;
(3)俯、侧视图都反映物体的宽度——“宽相等”.
要点三、斜二测画法
在立体几何中,空间几何体的直观图通常是在平行投影下画出的空间图形.要画空间几何体的直观图,首先要学会水平放置的平面图形的直观图画法.
对于平面多边形,我们常用斜二测画法画它们的直观图,斜二测画法是一种特殊的平行投影画法.
斜二测画法的步骤:
(1)在已知图形中取互相垂直的z轴和y轴,两轴相交于点O.画直观图时,把它们画成对应的x'轴与y'轴,两轴交于点O',且使∠x'O'y'=45°(或135°),它们确定的平面表示水平面.
(2)已知图形中,平行于x轴、y轴的线段,在直观图中分别画成平行于x'轴、y'轴的线段,并使它们和所画坐标轴的位置关系与已知图形中相应线段和原坐标轴的位置关系相同.
(3)已知图形中,平行于x轴或z轴的线段,在直观图中保持长度不变,平行于y轴的线段,长度变为原来的一半.画图完成后,擦去作为辅助线的坐标轴,就得到了平面图形的直观图.
要点诠释:
用斜二测画法画图的关键是在原图中找到决定图形位置与形状的点并在直观图中画出.一般情况下,这些点的位置都要通过其所在的平行于x、y轴的线段来确定,当原图中无需线段时,需要作辅助线段.
要点四、立体图形的直观图
(1)用斜二测画法画空间几何体的步骤
①在已知图形中,取互相垂直的x轴和y轴,再取z轴,使∠xOz=90°,且∠yOz=90°;
②画直观图时,把它们画成对应的轴x′,y′,z′,使∠x′O′y′=45°(或135°),∠x′O′z′=90°,x′O′y′所确定的平面表示水平平面;
③已知图形中平行于x轴,y轴或z轴的线段,在直观图中分别画成平行于x′轴,y′轴或z′轴的线段;
④在已知平面图形中平行于x轴和z轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度变为原来的一半;
⑤擦去作为辅助线的坐标轴,就得到了空间几何体的直观图.
(2)斜二测画法保留了原图形中的三个性质
①平行性不变,即在原图中平行的线在直观图中仍然平行;②共点性不变,即在原图中相交的直线仍然相交;③平行于x,z轴的长度不变.
(3)画立体图形与画水平放置的平面图形相比多了一个z轴,其直观图中对应于z轴的是z'轴,平面x'O'y'表示水平平面,平面y'O'z'和x'O'z'表示直立平面.平行于z轴(或在:轴上)的线段,其平行性和长度都不变.
(4)三视图与直观图的联系与区别
三视图与直观图都是用平面图形来刻画空间图形的位置特征与度量特征,二者有以下区别:
①三视图从细节上刻画了空间几何体的结构,由三视图可以得到一个精确的几何体,如零件、建筑图纸等都是三视图.
②直观图是对空间几何体的整体刻画,可视性高,立体感强,由此可以想象实物的形状.
要点五、已知三视图画直观图
三视图和直观图是空间几何体的两种不同的表现形式.直观图是在某一定点观察到的图形,三视图是投射线从不同位置将物体按正投影向投影面投射所得到的图形,对于同一个物体,两者可以相互转换.
由三视图画直观图,一般可分为两步:
第一步:想象空间几何体的形状.
三视图是按照正投影的规律,使平行光线分别从物体的正面、侧面和上面投射到投影面后得到的投影图,包括正视图、侧视图和俯视图.
正视图反映出物体的长和高,侧视图反映出物体高和宽,所以正视图和侧视图可以确定几何体的基本形状,如柱体、锥体或台体等.俯视图反映出物体的长和宽.对于简单几何体来说,当俯视图是圆形时,该几何体是旋转体;当俯视图是多边形时,该几何体是多面体.
第二步:利用斜二测画法画出直观图.
当几何体的形状确定后,用斜二测画法画出相应物体的直观图.注意用实线表示看得见的部分,用虚线表示看不见的部分.画完直观图后还应注意检验.
【典型例题】
类型一、平行投影与中心投影
例1.下列命题中正确的是( )
A.矩形的平行投影一定是矩形
B.梯形的平行投影一定是梯形
C.两条相交直线的投影可能平行
D.一条线段的平行投影如果仍是一条线段,那么这条线段中点的投影必是这条线段投影的中心
【答案】D
【解析】平行投影因投影线的方向变化而不同,因而平行投影改变几何图形的形状,因而A、B不正确.
两条直线的交点无论是平行投影还是中心投影仍是同一个点,这个点在两条直线的投影上,因而两条直线的投影不可能平行,故C错.
两条线段平行投影的比等于这两条线段的比,因而D正确.
【总结升华】空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线,如照片中由近到远,物体之间的距离越来越近,最后相交于一点.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体,所以在绘画时,经常使用这种方法.
例2.一图形的投影是一条线段,这个图形不可能是 .
①线段 ②直线 ③圆 ④梯形 ⑤长方体
【答案】②⑤
【解析】线段、圆、梯形都是平面图形,且在有限范围内,投影都可能为线段;长方体是三维空间图形,其投影不可能是线段;直线的投影,只能是直线或点.
举一反三:
【变式1】有下列说法:
①从投影的角度看,三视图和斜二测画法画出的直观图都是平行投影下画出来的空间图形;②平行投影的投影线互相平行,中心投影的投影线相交于一点;③空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线;④空间几何体在平行投影与中心投影下有不同的表现形式.
其中正确的命题有( ).
A.1个 B.2个 C.3个 D.4个
【答案】D
类型二、空间几何体的三视图
例3.螺栓是棱柱和圆柱构成的组合体,如下图,画出它的三视图.
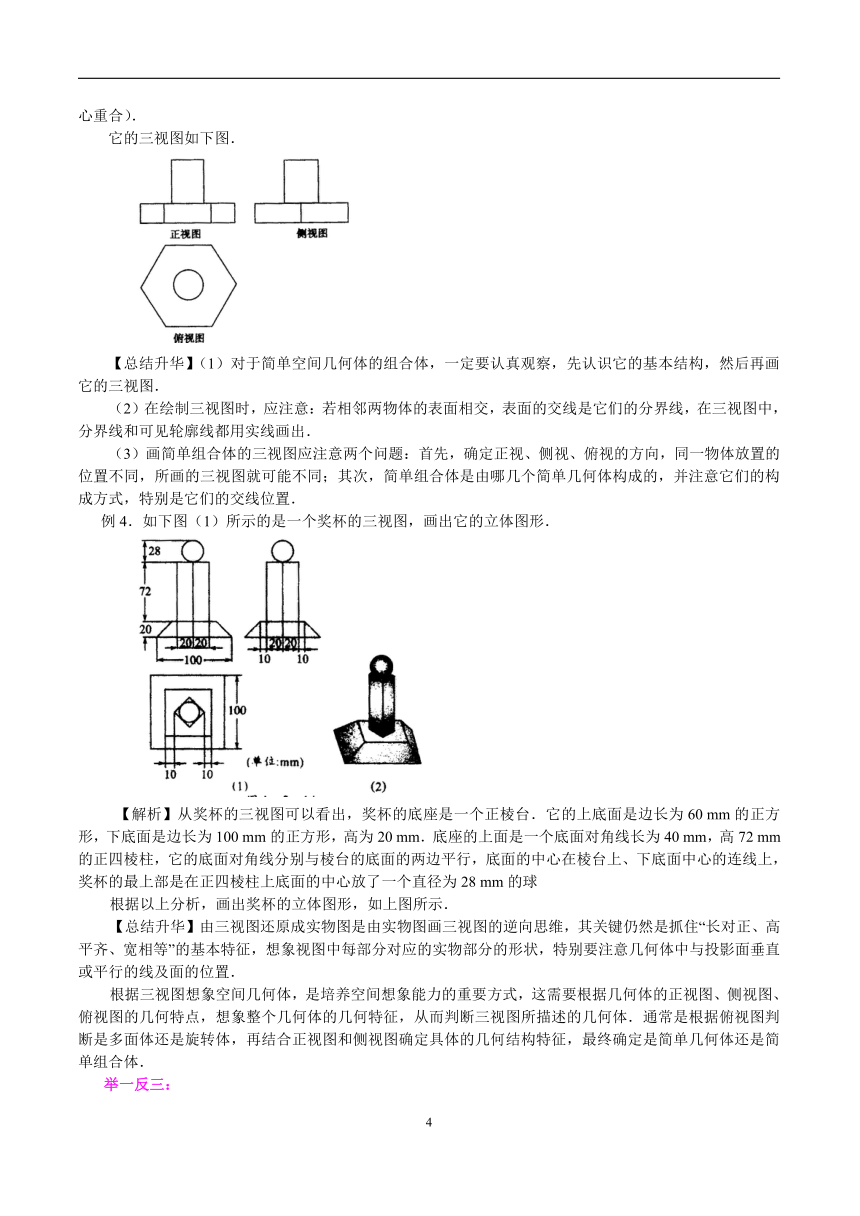
【解析】该物体是由一个正六棱柱和一个圆柱组合而成的.正视图反映正六棱柱的三个侧面和圆柱侧面,侧视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体正投影后是一个正六边形和一个圆(中心重合).
它的三视图如下图.
【总结升华】(1)对于简单空间几何体的组合体,一定要认真观察,先认识它的基本结构,然后再画它的三视图.
(2)在绘制三视图时,应注意:若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出.
(3)画简单组合体的三视图应注意两个问题:首先,确定正视、侧视、俯视的方向,同一物体放置的位置不同,所画的三视图就可能不同;其次,简单组合体是由哪几个简单几何体构成的,并注意它们的构成方式,特别是它们的交线位置.
例4.如下图(1)所示的是一个奖杯的三视图,画出它的立体图形.
【解析】从奖杯的三视图可以看出,奖杯的底座是一个正棱台.它的上底面是边长为60 mm的正方形,下底面是边长为100 mm的正方形,高为20 mm.底座的上面是一个底面对角线长为40 mm,高72 mm的正四棱柱,它的底面对角线分别与棱台的底面的两边平行,底面的中心在棱台上、下底面中心的连线上,奖杯的最上部是在正四棱柱上底面的中心放了一个直径为28 mm的球
根据以上分析,画出奖杯的立体图形,如上图所示.
【总结升华】由三视图还原成实物图是由实物图画三视图的逆向思维,其关键仍然是抓住“长对正、高平齐、宽相等”的基本特征,想象视图中每部分对应的实物部分的形状,特别要注意几何体中与投影面垂直或平行的线及面的位置.
根据三视图想象空间几何体,是培养空间想象能力的重要方式,这需要根据几何体的正视图、侧视图、俯视图的几何特点,想象整个几何体的几何特征,从而判断三视图所描述的几何体.通常是根据俯视图判断是多面体还是旋转体,再结合正视图和侧视图确定具体的几何结构特征,最终确定是简单几何体还是简单组合体.
举一反三:
【变式1】 右图是长和宽分别相等的两个矩形.给定下列三个命题,其中真命题的个数是( ).
①存在三棱柱.其正(主)视图、俯视图如右图 ②存在四棱柱,其正(主)视图、俯视图如右图 ③存在圆柱,其正(主)视图、俯视图如右图
A.3 B.2 C.1 D.0
【答案】A
【变式2】一几何体的直观图如图,下列给出的四个俯视图中正确的是( )
【答案】B
【解析】由直观图可知,该几何体由一个长方体和一个截角三棱柱组成,从上往下看,外层轮廓线是一矩形,矩形内部有一条线段连接两个三角形.故选B.
类型三、空间几何体的直观图
例5.如图所示,梯形ABCD中,AB∥CD,AB=4 cm,CD=2 cm,∠DAB=30°,AD=3 cm,试画出它的直观图.
【答案】详见解析
【解析】(1)如图a所示,在梯形ABCD中,以边AB所在的直线为x轴,点A为原点,建立平面直角坐标系xOy.如图b所示,画出对应的x′轴,y′轴,使∠x′O′y′=45°.
(2)在图a中,过D点作DE⊥x轴,垂足为E.在x′轴上取A′B′=AB=4 cm,A′E′=AE=≈2.598 cm;过点E′作E′D′∥y′轴,使,再过点D′作D′C′∥x′轴,且使D′C′=DC=2 cm.
(3)连接A′D′、B′C′,并擦去x′轴与y′轴及其他一些辅助线,如图c所示,则四边形A′B′C′D′就是所求作的直观图.
【总结升华】斜二测画法的作图技巧:
1.在已知图中建立直角坐标系,理论上在任何位置建立坐标系都行,但实际作图时,一般建立特殊的直角坐标系,尽量运用原有直线为坐标轴或图形的对称轴为坐标轴,以线段的中点或图形的对称点为原点;
2.在原图中平行于轴和轴的线段在直观图中仍然平行于轴和轴,原图中不与坐标轴平行的线段可以先画出线段的端点再连线,画端点时利用与坐标轴平行的线段;
3.画立体图形的直观图,在画轴时,要再画一条与平面垂直的轴,平行于轴的线段长度保持不变.
举一反三:
【变式1】已知正角形ABC的边长为a,那么△ABC的平面直观图△A'B'C'的面积为( )
A. B. C. D.
【答案】D
【解析】先根据题意,画出直观图,然后根据直观图△A'B'C'的边长及夹角求解.
如上图(1)、(2)所示的实际图形和直观图.由图(2)可知,A'B'=AB=a,,在图(2)中作C'D'⊥A'B'于D',则.
∴.
【总结升华】求直观图的面积的关键是依据斜二测画法,求出相应的直观图的底边和高,也就是原来实际图形中的高线在直观图中变为与水平直线成45°角且长度为原来的一半的线段,以此为依据求出相应的高线即可.反过来,由一个平面图形的直观图来确定原平面图形的面积,也是依据这个规则来确定的.
例6.(2017春 福建漳州月考)已知某几何体的三视图如图,画出该几何体的直观图.
【思路点拨】这是底面边长为4,高为2的同底的正四棱柱与四棱锥的组合体,可得该几何体的直观图;
【解析】几何体的直观图如图.
【巩固练习】
1.下列实例中,不是中心投影的是( ).
A.工程图纸 B.小孔成像 C.相片 D.人的视觉
2.下列种说法:①相等的角在直观图中对应的角仍然相等;②相等的线段在直观图中对应的线段仍然相等;③平行的线段在直观图中对应的线段仍然平行;④线段的中点在直观图中仍然是线段的中点.其中,说法正确的有( ).
A.1个 B.2个 C.3个 D.4个
3.一个几何体的某一方向的视图是圆,则它不可能是( ).
A.球体 B.圆锥 C.圆柱 D.长方体
4.一个建筑物的正视图、侧视图、俯视图如下图所示,则组成这个建筑物的组合体是( ).
A.圆柱和圆锥 B.立方体和圆锥 C.正四棱柱和圆锥 D.正方形和圆
5.观察下图所示几何体,其中判断正确的是( )
A.①是棱台 B.②是圆台
C.③是棱锥 D.④不是棱柱
6.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为
7.平行投影与中心投影之间的区别是________________.
8.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为____________.
9.(2017 大庆模拟)某几何体是由大小相同的正方体木块堆成的,其正视图、侧视图均如图所示,则此几何体最少由________块木块堆成.
10.用斜二测画法作出两边边长分别为3cm和4cm的矩形的直观图.
11.已知正三角形ABC的边长为a,求△ABC的直观图△A′B′C′的面积.
12.(2017 安吉县月考)(1)用斜二测画法作出边长为3 cm、高4 cm的矩形的直观图;
(2)画出正四棱锥的三视图.
【答案与解析】
1.【答案】A
【解析】由中心投影的特点可知,B、C、D均是中心投影.
2.【答案】B
【解析】由直观图的画法可知③、④正确.
3.【答案】D
【解析】
4.【答案】C
【解析】 由三视图可知,组合体上部分是圆锥,下部分为正四棱柱.
5.【答案】C
6.【答案】C
【解析】 正视图中小长方形在左上方,对应俯视图应该在左侧,排除B、D,侧视图中小长方形在右上方,对应俯视图应该在下方,排除A,故选C.
7.【答案】平行投影的投影线互相平行,而中心投影的投影线相交于一点.
8.【答案】2.5
【解析】由直观图知,原平面图形为直角三角形,且AC=A′C′=3,BC=2B′C′=4,计算得AB=5,所求中线长为2.5.
9.【答案】5
【解析】由三视图可知这几个正方体木块有三层,
底层至少有3个小正方体,第2层和第3层至少有一个小正方体,
所以该几何至少共有3+1+1=5块正方体,
故答案为:5.
10.【解析】采用斜二测画法,即在已知图形所在的空间中取水平平面,作轴、轴,使,然后依据平行投影的有关性质逐一作图(如右图).
(1)在已知ABCD中取AB,AD所在边为x轴与y轴,相交于点O(O与A重合),画对应的x'轴、y'轴,使∠x'O'y'=45°.
(2)在x'轴上取A',B',使A'B'=AB=4,在y'轴上取D',使A'D'=AD=,过D'作D'C'平行x'的直线,且等于A'B'长.
(3)连C'B',所得四边形A'B'C'D'就是矩形ABCD的直观图.
11.【答案】
【解析】先画出正三角形ABC,
然后再画出它的水平放置的直观图,
如图所示.由斜二测画法规则知
B′C′=a,O′A′=.
过A′引A′M⊥x′轴,垂足为M,
则A′M=O′A′·sin 45°=.
∴S△A′B′C′=B′C′·A′M
=.
12.【解析】(1)①在已知ABCD中取AB、AD所在边为X轴与Y辆,相交于O点(O与A重合),
画对应X'轴,Y'轴使∠X'O'Y=45°
②在X'轴上取A',B'使A'B'=AB,在Y'轴上取D',
使,对D'作D'C'平行X'的直线,且等于A'D'长.
③连C'B'所得四边形A'B'C'D'就是矩形ABCD的直观图.
(2)正四棱锥的正视图与侧视图是相同的等腰三角形,俯视图轮廓是正方形,含有对角线,如图:
【学习目标】
1.了解平行投影与中心投影,了解在平行投影下画空间图形与在中心投影下画空间图形两种方法的各自特点,了解空间图形的不同表现形式;
2. 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱的简易组合体)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测画法画出它们的直观图.
【要点梳理】
要点一、中心投影与平行投影
1.投影、投影线和投影面
由于光的照射,在不透明物体后面的屏幕上可以留下这个物体的影子,这种现象叫做投影.其中的光线叫做投影线,留下物体影子的屏幕叫做投影面.
2.中心投影
我们把光由一点向外散射形成的投影叫做中心投影.中心投影的投影线交于一点,它的实质是一个点光源把一个物体射到一个平面上,这个物体的影子就是它在这个平面上的中心投影.
3.中心投影的性质
(1)中心投影的投影线交于一点;
(2)点光源距离物体越近,投影形成的影子越大.
4.平行投影
我们把在一束平行光线照射下形成的投影叫做平行投影.投影线正对着投影面时,叫做正投影,否则叫做斜投影.
5.平行投影的性质
(1)平行投影的投影线互相平行.
(2)在平行投影之下,与投影面平行的平面图形留下的影子与这个平面图形的形状和大小完全相同.
6.中心投影与平行投影的区别与联系
(1)平行投影包括斜二测画法和三视图.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.
(2)画实际效果图时,一般用中心投影法,画立体几何中的图形时,一般用平行投影法.
要点二、空间几何体的三视图
1.三视图的概念
把一个空间几何体投影到一个平面上,可以获得一个平面图形,但是只有一个平面图形很难把握几何体的全貌,因此我们需要从多个角度进行投影,这样才能较好地把握几何体的形状和大小.通常,我们总是选择三种投影.
(1)光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图;
(2)光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图;
(3)光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图.
几何体的正视图、侧视图和俯视图统称为几何体的三视图.
2.三视图的画法规则
画三视图时,以正视图为准,俯视图在正视图的正下方,侧视图在正视图的正右方,正、俯、侧三个视图之间必须互相对齐,不能错位.
正视图反映物体的长度和高度,俯视图反映物体的长度和宽度,侧视图反映物体的宽度和高度,由此,每两个视图之间有一定的对应关系,根据这种对应关系得到三视图的画法规则:
(1)正、俯视图都反映物体的长度——“长对正”;
(2)正、侧视图都反映物体的高度——“高平齐”;
(3)俯、侧视图都反映物体的宽度——“宽相等”.
要点三、斜二测画法
在立体几何中,空间几何体的直观图通常是在平行投影下画出的空间图形.要画空间几何体的直观图,首先要学会水平放置的平面图形的直观图画法.
对于平面多边形,我们常用斜二测画法画它们的直观图,斜二测画法是一种特殊的平行投影画法.
斜二测画法的步骤:
(1)在已知图形中取互相垂直的z轴和y轴,两轴相交于点O.画直观图时,把它们画成对应的x'轴与y'轴,两轴交于点O',且使∠x'O'y'=45°(或135°),它们确定的平面表示水平面.
(2)已知图形中,平行于x轴、y轴的线段,在直观图中分别画成平行于x'轴、y'轴的线段,并使它们和所画坐标轴的位置关系与已知图形中相应线段和原坐标轴的位置关系相同.
(3)已知图形中,平行于x轴或z轴的线段,在直观图中保持长度不变,平行于y轴的线段,长度变为原来的一半.画图完成后,擦去作为辅助线的坐标轴,就得到了平面图形的直观图.
要点诠释:
用斜二测画法画图的关键是在原图中找到决定图形位置与形状的点并在直观图中画出.一般情况下,这些点的位置都要通过其所在的平行于x、y轴的线段来确定,当原图中无需线段时,需要作辅助线段.
要点四、立体图形的直观图
(1)用斜二测画法画空间几何体的步骤
①在已知图形中,取互相垂直的x轴和y轴,再取z轴,使∠xOz=90°,且∠yOz=90°;
②画直观图时,把它们画成对应的轴x′,y′,z′,使∠x′O′y′=45°(或135°),∠x′O′z′=90°,x′O′y′所确定的平面表示水平平面;
③已知图形中平行于x轴,y轴或z轴的线段,在直观图中分别画成平行于x′轴,y′轴或z′轴的线段;
④在已知平面图形中平行于x轴和z轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度变为原来的一半;
⑤擦去作为辅助线的坐标轴,就得到了空间几何体的直观图.
(2)斜二测画法保留了原图形中的三个性质
①平行性不变,即在原图中平行的线在直观图中仍然平行;②共点性不变,即在原图中相交的直线仍然相交;③平行于x,z轴的长度不变.
(3)画立体图形与画水平放置的平面图形相比多了一个z轴,其直观图中对应于z轴的是z'轴,平面x'O'y'表示水平平面,平面y'O'z'和x'O'z'表示直立平面.平行于z轴(或在:轴上)的线段,其平行性和长度都不变.
(4)三视图与直观图的联系与区别
三视图与直观图都是用平面图形来刻画空间图形的位置特征与度量特征,二者有以下区别:
①三视图从细节上刻画了空间几何体的结构,由三视图可以得到一个精确的几何体,如零件、建筑图纸等都是三视图.
②直观图是对空间几何体的整体刻画,可视性高,立体感强,由此可以想象实物的形状.
要点五、已知三视图画直观图
三视图和直观图是空间几何体的两种不同的表现形式.直观图是在某一定点观察到的图形,三视图是投射线从不同位置将物体按正投影向投影面投射所得到的图形,对于同一个物体,两者可以相互转换.
由三视图画直观图,一般可分为两步:
第一步:想象空间几何体的形状.
三视图是按照正投影的规律,使平行光线分别从物体的正面、侧面和上面投射到投影面后得到的投影图,包括正视图、侧视图和俯视图.
正视图反映出物体的长和高,侧视图反映出物体高和宽,所以正视图和侧视图可以确定几何体的基本形状,如柱体、锥体或台体等.俯视图反映出物体的长和宽.对于简单几何体来说,当俯视图是圆形时,该几何体是旋转体;当俯视图是多边形时,该几何体是多面体.
第二步:利用斜二测画法画出直观图.
当几何体的形状确定后,用斜二测画法画出相应物体的直观图.注意用实线表示看得见的部分,用虚线表示看不见的部分.画完直观图后还应注意检验.
【典型例题】
类型一、平行投影与中心投影
例1.下列命题中正确的是( )
A.矩形的平行投影一定是矩形
B.梯形的平行投影一定是梯形
C.两条相交直线的投影可能平行
D.一条线段的平行投影如果仍是一条线段,那么这条线段中点的投影必是这条线段投影的中心
【答案】D
【解析】平行投影因投影线的方向变化而不同,因而平行投影改变几何图形的形状,因而A、B不正确.
两条直线的交点无论是平行投影还是中心投影仍是同一个点,这个点在两条直线的投影上,因而两条直线的投影不可能平行,故C错.
两条线段平行投影的比等于这两条线段的比,因而D正确.
【总结升华】空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线,如照片中由近到远,物体之间的距离越来越近,最后相交于一点.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体,所以在绘画时,经常使用这种方法.
例2.一图形的投影是一条线段,这个图形不可能是 .
①线段 ②直线 ③圆 ④梯形 ⑤长方体
【答案】②⑤
【解析】线段、圆、梯形都是平面图形,且在有限范围内,投影都可能为线段;长方体是三维空间图形,其投影不可能是线段;直线的投影,只能是直线或点.
举一反三:
【变式1】有下列说法:
①从投影的角度看,三视图和斜二测画法画出的直观图都是平行投影下画出来的空间图形;②平行投影的投影线互相平行,中心投影的投影线相交于一点;③空间图形经过中心投影后,直线变成直线,但平行线可能变成了相交的直线;④空间几何体在平行投影与中心投影下有不同的表现形式.
其中正确的命题有( ).
A.1个 B.2个 C.3个 D.4个
【答案】D
类型二、空间几何体的三视图
例3.螺栓是棱柱和圆柱构成的组合体,如下图,画出它的三视图.
【解析】该物体是由一个正六棱柱和一个圆柱组合而成的.正视图反映正六棱柱的三个侧面和圆柱侧面,侧视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体正投影后是一个正六边形和一个圆(中心重合).
它的三视图如下图.
【总结升华】(1)对于简单空间几何体的组合体,一定要认真观察,先认识它的基本结构,然后再画它的三视图.
(2)在绘制三视图时,应注意:若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出.
(3)画简单组合体的三视图应注意两个问题:首先,确定正视、侧视、俯视的方向,同一物体放置的位置不同,所画的三视图就可能不同;其次,简单组合体是由哪几个简单几何体构成的,并注意它们的构成方式,特别是它们的交线位置.
例4.如下图(1)所示的是一个奖杯的三视图,画出它的立体图形.
【解析】从奖杯的三视图可以看出,奖杯的底座是一个正棱台.它的上底面是边长为60 mm的正方形,下底面是边长为100 mm的正方形,高为20 mm.底座的上面是一个底面对角线长为40 mm,高72 mm的正四棱柱,它的底面对角线分别与棱台的底面的两边平行,底面的中心在棱台上、下底面中心的连线上,奖杯的最上部是在正四棱柱上底面的中心放了一个直径为28 mm的球
根据以上分析,画出奖杯的立体图形,如上图所示.
【总结升华】由三视图还原成实物图是由实物图画三视图的逆向思维,其关键仍然是抓住“长对正、高平齐、宽相等”的基本特征,想象视图中每部分对应的实物部分的形状,特别要注意几何体中与投影面垂直或平行的线及面的位置.
根据三视图想象空间几何体,是培养空间想象能力的重要方式,这需要根据几何体的正视图、侧视图、俯视图的几何特点,想象整个几何体的几何特征,从而判断三视图所描述的几何体.通常是根据俯视图判断是多面体还是旋转体,再结合正视图和侧视图确定具体的几何结构特征,最终确定是简单几何体还是简单组合体.
举一反三:
【变式1】 右图是长和宽分别相等的两个矩形.给定下列三个命题,其中真命题的个数是( ).
①存在三棱柱.其正(主)视图、俯视图如右图 ②存在四棱柱,其正(主)视图、俯视图如右图 ③存在圆柱,其正(主)视图、俯视图如右图
A.3 B.2 C.1 D.0
【答案】A
【变式2】一几何体的直观图如图,下列给出的四个俯视图中正确的是( )
【答案】B
【解析】由直观图可知,该几何体由一个长方体和一个截角三棱柱组成,从上往下看,外层轮廓线是一矩形,矩形内部有一条线段连接两个三角形.故选B.
类型三、空间几何体的直观图
例5.如图所示,梯形ABCD中,AB∥CD,AB=4 cm,CD=2 cm,∠DAB=30°,AD=3 cm,试画出它的直观图.
【答案】详见解析
【解析】(1)如图a所示,在梯形ABCD中,以边AB所在的直线为x轴,点A为原点,建立平面直角坐标系xOy.如图b所示,画出对应的x′轴,y′轴,使∠x′O′y′=45°.
(2)在图a中,过D点作DE⊥x轴,垂足为E.在x′轴上取A′B′=AB=4 cm,A′E′=AE=≈2.598 cm;过点E′作E′D′∥y′轴,使,再过点D′作D′C′∥x′轴,且使D′C′=DC=2 cm.
(3)连接A′D′、B′C′,并擦去x′轴与y′轴及其他一些辅助线,如图c所示,则四边形A′B′C′D′就是所求作的直观图.
【总结升华】斜二测画法的作图技巧:
1.在已知图中建立直角坐标系,理论上在任何位置建立坐标系都行,但实际作图时,一般建立特殊的直角坐标系,尽量运用原有直线为坐标轴或图形的对称轴为坐标轴,以线段的中点或图形的对称点为原点;
2.在原图中平行于轴和轴的线段在直观图中仍然平行于轴和轴,原图中不与坐标轴平行的线段可以先画出线段的端点再连线,画端点时利用与坐标轴平行的线段;
3.画立体图形的直观图,在画轴时,要再画一条与平面垂直的轴,平行于轴的线段长度保持不变.
举一反三:
【变式1】已知正角形ABC的边长为a,那么△ABC的平面直观图△A'B'C'的面积为( )
A. B. C. D.
【答案】D
【解析】先根据题意,画出直观图,然后根据直观图△A'B'C'的边长及夹角求解.
如上图(1)、(2)所示的实际图形和直观图.由图(2)可知,A'B'=AB=a,,在图(2)中作C'D'⊥A'B'于D',则.
∴.
【总结升华】求直观图的面积的关键是依据斜二测画法,求出相应的直观图的底边和高,也就是原来实际图形中的高线在直观图中变为与水平直线成45°角且长度为原来的一半的线段,以此为依据求出相应的高线即可.反过来,由一个平面图形的直观图来确定原平面图形的面积,也是依据这个规则来确定的.
例6.(2017春 福建漳州月考)已知某几何体的三视图如图,画出该几何体的直观图.
【思路点拨】这是底面边长为4,高为2的同底的正四棱柱与四棱锥的组合体,可得该几何体的直观图;
【解析】几何体的直观图如图.
【巩固练习】
1.下列实例中,不是中心投影的是( ).
A.工程图纸 B.小孔成像 C.相片 D.人的视觉
2.下列种说法:①相等的角在直观图中对应的角仍然相等;②相等的线段在直观图中对应的线段仍然相等;③平行的线段在直观图中对应的线段仍然平行;④线段的中点在直观图中仍然是线段的中点.其中,说法正确的有( ).
A.1个 B.2个 C.3个 D.4个
3.一个几何体的某一方向的视图是圆,则它不可能是( ).
A.球体 B.圆锥 C.圆柱 D.长方体
4.一个建筑物的正视图、侧视图、俯视图如下图所示,则组成这个建筑物的组合体是( ).
A.圆柱和圆锥 B.立方体和圆锥 C.正四棱柱和圆锥 D.正方形和圆
5.观察下图所示几何体,其中判断正确的是( )
A.①是棱台 B.②是圆台
C.③是棱锥 D.④不是棱柱
6.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为
7.平行投影与中心投影之间的区别是________________.
8.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为____________.
9.(2017 大庆模拟)某几何体是由大小相同的正方体木块堆成的,其正视图、侧视图均如图所示,则此几何体最少由________块木块堆成.
10.用斜二测画法作出两边边长分别为3cm和4cm的矩形的直观图.
11.已知正三角形ABC的边长为a,求△ABC的直观图△A′B′C′的面积.
12.(2017 安吉县月考)(1)用斜二测画法作出边长为3 cm、高4 cm的矩形的直观图;
(2)画出正四棱锥的三视图.
【答案与解析】
1.【答案】A
【解析】由中心投影的特点可知,B、C、D均是中心投影.
2.【答案】B
【解析】由直观图的画法可知③、④正确.
3.【答案】D
【解析】
4.【答案】C
【解析】 由三视图可知,组合体上部分是圆锥,下部分为正四棱柱.
5.【答案】C
6.【答案】C
【解析】 正视图中小长方形在左上方,对应俯视图应该在左侧,排除B、D,侧视图中小长方形在右上方,对应俯视图应该在下方,排除A,故选C.
7.【答案】平行投影的投影线互相平行,而中心投影的投影线相交于一点.
8.【答案】2.5
【解析】由直观图知,原平面图形为直角三角形,且AC=A′C′=3,BC=2B′C′=4,计算得AB=5,所求中线长为2.5.
9.【答案】5
【解析】由三视图可知这几个正方体木块有三层,
底层至少有3个小正方体,第2层和第3层至少有一个小正方体,
所以该几何至少共有3+1+1=5块正方体,
故答案为:5.
10.【解析】采用斜二测画法,即在已知图形所在的空间中取水平平面,作轴、轴,使,然后依据平行投影的有关性质逐一作图(如右图).
(1)在已知ABCD中取AB,AD所在边为x轴与y轴,相交于点O(O与A重合),画对应的x'轴、y'轴,使∠x'O'y'=45°.
(2)在x'轴上取A',B',使A'B'=AB=4,在y'轴上取D',使A'D'=AD=,过D'作D'C'平行x'的直线,且等于A'B'长.
(3)连C'B',所得四边形A'B'C'D'就是矩形ABCD的直观图.
11.【答案】
【解析】先画出正三角形ABC,
然后再画出它的水平放置的直观图,
如图所示.由斜二测画法规则知
B′C′=a,O′A′=.
过A′引A′M⊥x′轴,垂足为M,
则A′M=O′A′·sin 45°=.
∴S△A′B′C′=B′C′·A′M
=.
12.【解析】(1)①在已知ABCD中取AB、AD所在边为X轴与Y辆,相交于O点(O与A重合),
画对应X'轴,Y'轴使∠X'O'Y=45°
②在X'轴上取A',B'使A'B'=AB,在Y'轴上取D',
使,对D'作D'C'平行X'的直线,且等于A'D'长.
③连C'B'所得四边形A'B'C'D'就是矩形ABCD的直观图.
(2)正四棱锥的正视图与侧视图是相同的等腰三角形,俯视图轮廓是正方形,含有对角线,如图:
