高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):09【基础】平面的基本性质
文档属性
| 名称 | 高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):09【基础】平面的基本性质 |
|
|
| 格式 | zip | ||
| 文件大小 | 496.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 00:00:00 | ||
图片预览




文档简介
平面
【学习目标】
1.利用生活中的实物对平面进行描述;理解平面的概念,掌握平面的画法及表示方法.
2.重点掌握平面的基本性质.
3.能利用平面的性质解决有关问题.
【要点梳理】
要点一、平面的基本概念
1.平面的概念:
“平面”是一个只描述而不定义的原始概念,常见的桌面、黑板面、平静的水面等都给我们以平面的形象.几何里的平面就是从这些物体中抽象出来的,但是,几何里的平面是无限延展的.
要点诠释:
(1)“平面”是平的(这是区别“平面”与“曲面”的依据);
(2) “平面”无厚薄之分;
(3)“平面”无边界,它可以向四周无限延展,这是区别“平面”与“平面图形”的依据.
2.平面的画法:
通常画平行四边形表示平面.
要点诠释:
(1)表示平面的平行四边形,通常把它的锐角画成,横边长是其邻边的两倍;
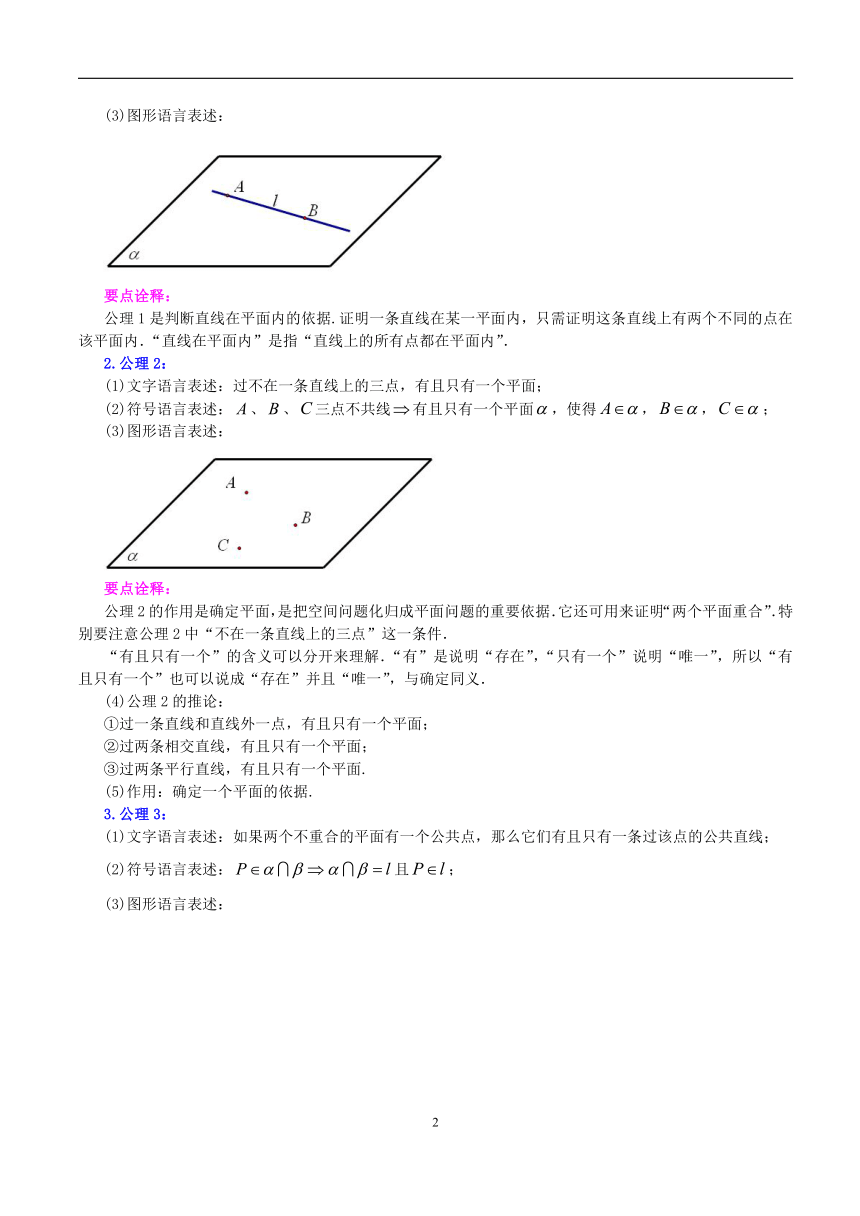
(2)两个相交平面的画法:当一个平面的一部分被另一个平面遮住时,把被遮住的部分的线段画为虚线或者不画;
3.平面的表示法:
(1)用一个希腊字母表示一个平面,如平面、平面、平面等;
(2)用表示平面的平行四边形的四个字母表示,如平面;
(3)用表示平面的平行四边形的相对两个顶点的两个字母表示,如平面或者平面;
4.点、直线、平面的位置关系:
(1)点A在直线a上,记作;点A在直线a外,记作;
(2)点A在平面上,记作;点A在平面外,记作;
(3)直线在平面内,记作;直线不在平面内,记作.
要点二、平面的基本性质
平面的基本性质即书中的三个公理,它们是研究立体几何的基本理论基础.
1.公理1:
(1)文字语言表述:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内;
(2)符号语言表述:,,,;
(3)图形语言表述:
要点诠释:
公理1是判断直线在平面内的依据.证明一条直线在某一平面内,只需证明这条直线上有两个不同的点在该平面内.“直线在平面内”是指“直线上的所有点都在平面内”.
2.公理2:
(1)文字语言表述:过不在一条直线上的三点,有且只有一个平面;
(2)符号语言表述:、、三点不共线有且只有一个平面,使得,,;
(3)图形语言表述:
要点诠释:
公理2的作用是确定平面,是把空间问题化归成平面问题的重要依据.它还可用来证明“两个平面重合”.特别要注意公理2中“不在一条直线上的三点”这一条件.
“有且只有一个”的含义可以分开来理解.“有”是说明“存在”,“只有一个”说明“唯一”,所以“有且只有一个”也可以说成“存在”并且“唯一”,与确定同义.
(4)公理2的推论:
①过一条直线和直线外一点,有且只有一个平面;
②过两条相交直线,有且只有一个平面;
③过两条平行直线,有且只有一个平面.
(5)作用:确定一个平面的依据.
3.公理3:
(1)文字语言表述:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线;
(2)符号语言表述:且;
(3)图形语言表述:
要点诠释:
公理3的作用是判定两个平面相交及证明点在直线上的依据.
要点三、证明点线共面
所谓点线共面问题就是指证明一些点或直线在同一个平面内的问题.
1.证明点线共面的主要依据:
(1)如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内(公理1);②经过不在同一条直线上的三点,有且只有一个平面(公理2及其推论).
2.证明点线共面的常用方法:
(1)纳入平面法:先确定一个平面,再证明有关点、线在此平面内;(2)辅助平面法:先证明有关的点、线确定平面α,再证明其余元素确定平面β,最后证明平面a、β重合;(3)反证法.
3.具体操作方法:
(1)证明几点共面的问题可先取三点(不共线的三点)确定一个平面,再证明其余各点都在这个平面内;
(2)证明空间几条直线共面问题可先取两条(相交或平行)直线确定一个平面,再证明其余直线均在这个平面内.
要点四、证明三点共线问题
所谓点共线问题就是证明三个或三个以上的点在同—条直线上.
1.证明三点共线的依据是公理3:如果两个不重合的平面有一个公共点,那么它们还有其他的公共点,且所有这些公共点的集合是一条过这个公共点的直线.也就说一个点若是两个平面的公共点,则这个点在这两个平面的交线上.
对于这个公理应进一步理解下面三点:①如果两个相交平面有两个公共点,那么过这两点的直线就是它们的交线;②如果两个相交平面有三个公共点,那么这三点共线;③如果两个平面相交,那么一个平面内的直线和另一个平面的交点必在这两个平面的交线上.
2.证明三点共线的常用方法
方法1:首先找出两个平面,然后证明这三点都是这两个平面的公共点.根据公理3知,这些点都在交线上.
方法2:选择其中两点确定一条直线,然后证明另一点也在其上.
要点五、证明三线共点问题
所谓线共点问题就是证明三条或三条以上的直线交于一点.
1.证明三线共点的依据是公理3.
2.证明三线共点的思路:先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.
【经典例题】
类型一、平面的概念及其表示
例1.下面的说法中正确的是( ).
A.平行四边形是一个平面
B.任何一个平面图形都是一个平面
C.平静的太平洋面就是一个平面
D.圆和平行四边形都可以表示平面
【答案】D
【解析】 利用平面的基本特征以及平面与平面图形的区别进行判断.
A不正确.我们用平行四边形来表示平面,但不能说平行四边形是一个平面.平行四边形仅是平面上四条线段构成的图形,它是不能无限延展的.
B不正确,平面图形和平面是完全不同的两个概念,平面图形是有大小的,它是不可以无限延展的.
C不正确,太平洋再大也会有边际,也不可能是绝对平面.
D正确.在需要时,除用平行四边形表示平面外,还能用三角形、梯形、圆等来表示平面.
【总结升华】 平面与平面图形既有区别又有联系.平面没有角度、绝对平展、无边界,是一种理想的图形.平面可以用三角形、正方形、梯形、圆等平面图形来表示.但平面图形如三角形、正方形、梯形等,它们是有大小之分的,不能说三角形、正方形、梯形等是平面.
举一反三:
【变式1】下列命题:
(1)书桌面是平面;(2)8个平面重叠起来要比6个平面重叠起来厚;(3)有一个平面的长是50 m,宽是20 m;(4)平面是绝对的平、无厚度、可以无限延展的抽象的数学概念.
其中正确命题的个数为( ).
A.1 B.2 C.3 D.4
【答案】A
例2.平面内的直线a、b相交于点P,用符号语言概述为“,且P∈ ”,是否正确?
【答案】不正确
【解析】不正确.应表示为:,,且a∩b=P.
相交于点P的直线a、b都在平面内,也可以说,平面经过相交于点P的直线a、b.题中的符号语言只描述了直线a、b交于点P,点P在平面内,而没有描述直线a、b也都在平面内,下图也是题中的符号语言所表示的情形.
【总结升华】用符号语言来叙述时,必须交代清楚所有元素的位置关系,不能有半点遗漏.
立体几何中的三种语言(文字语言、符号语言、图形语言组成立体几何语言,我们强须准确地把握它们.其中文字语言比较自然、生动,能将问题研究的对象的含义更明确地叙述出来.图形语言给人以清晰的视觉形象,有助于空间想象力的培养;而符号语言更精练、简洁.三种语言的互译有助于我们在更广阔的思维领域里寻找解决问题的途径,有利于对思维广阔性的培养.
举一反三:
【变式1】指出图中的图形画法是否正确,如不正确,请改正.
(1)如图1,直线a在平面α内.
(2)如图2,直线a和平面α相交.
(3)如图3,直线a和平面α平行.
【答案】详见解析
【解析】(1)(2)(3)的图形画法都不正确.正确画法如下图:
(1)直线a在平面α内:
(2)直线a与平面α相交:
(3)直线a与平面α平行:
类型二、平面的确定
例3.判断下列说法是否正确,并说明理由:
(1)一点和一条直线确定一个平面;
(2)经过一点的两条直线确定一个平面:
(3)两两相交的三条直线确定一个平面;
(4)首尾依次相接的4条线段在同一平面内.
【答案】不正确 正确 不正确 不正确
【解析】(1)不正确.如果点在直线上,可以确定无数个平面;如果点不在直线上,在已知直线上任取两个不同的点,由公理2知,有且只有一个平面,或直接由公理2的推论1知,有且只有一个平面.
(2)正确.经过同一点的两条直线是相交直线,由公理2的推论2知,有且只有一个平面.
(3)不正确.3条直线可能交于同一点,也可能有三个不同交点,如下图(1)、(2)所示.前者,由公理2的推论2知.可以确定1个或3个平面;后者,由公理2的推论2及公理1知,能确定一个平面.
(4)不正确.四边形中三点可确定一个平面,而第4点不一定在此平面内,如上图(3),因此这4条线段不一定在同一平面内.
【总结升华】公理2及其3个推论都是确定平面的依据,对涉及这方面的应用问题,务必分清它们的条件.立体几何研究的对象是空间点、线、面的位置关系问题,要有一定的空间想象能力.对于问题中的点、线,要注意它们各种不同的位置关系,以及由此产生的不同结果.
举一反三:
【变式1】正方体的八个顶点一共可以确定 个平面.
【答案】20
例4.三个互不重合的平面,能把空间分成n部分,则n的所有可能值为______________.
【思路点拨】将互不重合的三个平面的位置关系分为:三个平面互相平行;三个平面有两个平行,第三个平面与其它两个平面相交;三个平面交于一线;三个平面两两相交且三条交线平行;三个平面两两相交且三条交线交于一点;五种情况并分别讨论,即可得到答案.
【答案】4,6,7,8
【解析】若三个平面互相平行,则可将空间分为4部分;
若三个平面有两个平行,第三个平面与其它两个平面相交,则可将空间分为6部分;
若三个平面交于一线,则可将空间分为6部分;
若三个平面两两相交且三条交线平行(联想三棱柱三个侧面的关系),则可将空间分为7部分;
若三个平面两两相交且三条交线交于一点(联想墙角三个墙面的关系),则可将空间分为8部分;
故n等于4,6,7或8
类型三、平面的基本性质的应用
例5.如右图,在正方体ABCD-A1B1C1D1中,判断下列命题是否正确,并说明理由.
(1)直线AC1在平面CC1B1B内;
(2)设正方形ABCD与正方形A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
(3)由点A、D、C可以确定一个平面;
(4)由点A、C1、B1确定的平面为ADC1B1;
(5)由点A、C1、B1确定的平面与由点A、C1、D确定的平面是同一个平面.
【解析】(1)错误.因为点A平面CC1B1B,所以AC1不在平面CC1B1B内.
(2)正确.因为点O∈直线AC,直线AC平面AA1C1C,所以点O∈平面AA1C1C.同理,点O1∈平面AA1C1C,所以直线OO1平面AA1C1C.同理,直线OO1平面BB1D1D.故OO1为平面AA1C1C与平面BB1D1D的交线.
(3)错误.因为点A、O、C在同一直线上,故不能确定—个平面
(4)正确.因为点A、C1、B1不共线,故可确定一个平面,又AD∥B1C1,所以点D∈平面AB1C1,故由点A、C1、B1确定的平面为ADC1B1.
(5)正确.因为点A、C1、B1确定的平面为平面ADC1B1,而由点A、C1、D确定的平面也是平面ADC1B1,故它们确定的是同一个平面.
【总结升华】正确地运用三个公理和有关概念的推理是解决此类题目的依据.
例6.已知直线a∥b,直线与a,b都相交,求证:过a,b,有且只有一个平面.
证明 证法一:如下图所示.由已知a∥b,所以过a,b有且只有一个平面.设,,∴A∈,B∈,且A∈,B∈,∴.即过a,b,有且只有一个平面.
证法二:由已知可设,.
∵,过与a有且只有一个平面.
∵a∥b,∴过a,b有且只有一个平面,
∴B∈,B∈,,.
又Ba,∴平面与重合.
即a∥b,.,过a,b,有且只有一个平面.
【总结升华】在证明多线共面时,可用下面的两种方法来证明:
(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平面内.确定一个平面的方法:①直线和直线外一点确定一个平面;②两条平行线确定一个平面;③两条相交直线确定一个平面.
(2)重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.
举一反三:
【变式】(1)空间两两相交的四条直线能确定几个平面?
(2)证明空间不共点且两两相交的四条直线在同一平面内.
【答案】(1)1或6;(2)略
【解析】(1)略
(2)分两种情形,有三条交于一个点,没有三条交于一个点.
已知:直线AB、BC、CD、DA两两相交,且不过同一点.
求证:直线AB、BC、CD、DA 共面.
证明:如图(左), AB、BC、CD、DA两两相交,且无三条直线相交于一点.
设 AD、BC 交于点M,AB、CD交于点N.∴ AB、CD确定一个平面α.
又∵ C∈CD,B∈AB,D∈CD,A∈AB.∴A、B、C、D∈α.
由公理1,知 AD、BC∈α .
故AB、BC、CD、DA 四条直线共面.
如图(右),AB、BC、CD、DA两两相交,且有三直线交于一点D.
∵ AB∩CD=C. ∴ AB、CD确定一个平面β.
又∵ A∈AB,D∈CD,∴A、D∈β,B∈AB,D∈CD,∴ B、D∈β.
∴ AD(β,BD(β(公理1).∴ AB、BC、CD、DA四直线共面.
例7.如下图,已知△ABC的三个顶点都不在平面内,它的三边AB、BC、AC延长后分别交平面 于点P、Q、R.求证:P、Q、R在同一条直线上.
证明 由已知AB的延长线交平面于点P,根据公理3,平面ABC与平面必相交于一条直线,设为L.
∵P∈直线AB,
∴P∈平面ABC.
又AB∩=P, ∴P∈平面,
∴P是平面ABC与平面的公共点.
∵平面ABC∩=,∴P∈,
同理,Q∈,R∈.
∴点P、Q、R在同一条直线上.
【总结升华】多点共线中的这条线一定是两个平面的交线,因此这类问题实际为两平面的相交问题.
举一反三:
【变式1】已知E,F,G,H分别是空间四边形各边AB,AD,BC,CD上的点,且直线EF与GH交于点P.求证:B,D,P在同一直线上.
【解析】
例8.(2017 甘肃天水月考)在正方体中,E为AB的中点,F为的中点,求证:CE,,DA三线共点.
【思路点拨】延长、DA交于P,连结EP,由已知条件得△PAE≌△PAF,从而得到∠PEA+∠AEC=180°,由此能证明CE、、DA三线共点于P.
【答案】略
【解析】延长、DA交于P,连结EP
∵AE=AF,PA=PA,∠PAE=∠PAF=90°,
∴△PAE≌△PAF,
∴∠PFA=∠PEA,
∵∠PEA=,=∠DCE(=∠BCE),
∴∠PEA=∠DCE,
又∵∠DCE+∠AEC=180°,
∴∠PEA+∠AEC=180°,
即点P、E、C共线,
∴CE,,DA三线共点于P.
【总结升华】本题考查三线共点的证明,题时要认真审题,注意空间思维能力的培养.
举一反三:
【变式1】 如下图,已知空间四边形ABCD(即四个点不在同一平面内的四边形)中,E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且.
求证:直线EF、GH、AC相交于一点.
证明:∵E、H分别是边AB、AD的中点,
∴EH∥BD且.
∵F、G分别是边BC、CD上的点,且,
∴FG∥BD且.
故知EH∥FGE且EH≠FG,
即四边形EFGH为梯形,从而EF与GH必相交,设交点为P.
∵P∈EF,EF平面ABC,∴P∈平面ABC.
同理P∈平面ADC.
∵平面ADC∩平面ABC=AC,∴P∈AC.
即EF、GH、AC交于一点P
【巩固练习】
1.“直线经过平面外一点”用符号表示为( )
A. B. C. D.
2.下面图形均表示两个相交平面,其中画法正确的是( )
3.已知平面α与平面β、γ都相交,则这三个平面可能的交线有( )
A.1条或2条 B.2条或3条
C.1条或3条 D.1条或2条或3条
4.下列说法正确的是( )
A.空间四边形的对角线可能相交
B.四个角都是直角的四边形一定是平面图形
C.两两相交的三条直线一定共面
D.在空间的四点,若无三点共线,则这四点一定不共面.
5.空间四点A,B,C,D共面而不共线,那么这四点中( ).
A.必有三点共线 B.必有三点不共线 C.至少有三点共线 D.不可能有三点共线
6.若三个平面把空间分成6个部分,那么这三个平面的位置关系是( )
A. 三个平面共线
B. 有两个平面平行且都与第三个平面相交
C. 三个平面共线,或两个平面平行且都与第三个平面相交
D.三个平面两两相交.
7.把下列符号叙述所对应的图形(如图)的序号填在题后横线上.
(1)Aα,a在平面α内________.
(2)α∩β=a,Pα且Pβ________.
(3)aα,a∩α=A________.
(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O________.
8.在空间四边形中,点分别在上,若直线与相交于点,则点与直线的关系是 .
9.(2017春 江苏启东市期末)若直线l上有两个点在平面α内,则下列说法正确的序号为________
①直线l上至少有一个点在平面α外;
②直线l上有无穷多个点在平面α外;
③直线l上所有点都在平面α内;
④直线l上至多有两个点在平面α内.
10.三个平面把空间分成7部分时它们的交线有 条.
11.画一个正方体ABCD-A1B1C1D1,再画出平面AC D1与平面BD C1的交线,并且说明理由.
12.(2017 安徽蚌埠月考)如图,已知E、F、G、H分别是三棱锥A—ABC的棱AB、BC、CD、DA的中点.
求证:E、F、G、H四点共面
13.若空间中三个平面两两相交于三条直线,这三条直线两两不平行,求证此三条直线必相交于一点.
【答案与解析】
1.C
【解析】 注意点与直线、点与平面之间的关系是元素与集合的关系,直线与平面之间的关系是集合与集合之间的关系.故选C.
2.【答案】D
【解析】 A中图形没有画出两平面的交线;B、C中图形的实、虚线没有按照画法原则去画,也不正确.故选D.
3.【答案】D
【解析】当α过平面β与γ的交线时,这三个平面有1条交线,
当β∥γ时,α与β和γ各有一条交线,共有2条交线.
当β∩γ=b,α∩β=a,α∩γ=c时,有3条交线.
故选D.
4.【答案】B
【解析】 空间四边形的对角线一定不相交,故A不正确;两两相交的三条直线能确定1或3个平面,故C不正确;在空间的四点,若无三点共线,则这四点可能共面也可能不共面,故D不正确.所以只有B正确.
5.【答案】B
【解析】 空间四点A,B,C,D共面而不共线,则至少有一点不在其余点中的两点确定的直线上.如CAB,无论C点在何位置,C,A,B不共线.故选B.
6.【答案】C
【解析】如下图,三个平面相交的截面图是下面两种情况时,把空间分成6个部分.
7.【答案】(1)C (2)D (3)A (4)B
8.【答案】
【解析】由公理3可得。
9.【答案】③
【解析】若直线l上有两个点在平面α内,则直线l在平面α内,
所以直线l上所有点都在平面α内.
所以正确的命题是③.
故答案为:③.
10.【答案】3
【解析】三个平面如图相交时,把空间分成7个部分,所以交线是3条.
11.【解析】如图,为所求.
12.【证明】依题意,EH为△ABD的中位线,
∴EH∥BD,
同理GF∥BD,
∴四边形EFGH为平行四边形,
∴E、F、G、H四点共面.
13.【证明】∵l1在平面β内,l2在平面β内,l1l2,
∴l1∩l2交于一点,记交点为P.
∵P∈l1在平面β内,P∈l2在平面γ内,
∴P∈β∩γ=l3,
∴l1,l2,l3交于一点.
【学习目标】
1.利用生活中的实物对平面进行描述;理解平面的概念,掌握平面的画法及表示方法.
2.重点掌握平面的基本性质.
3.能利用平面的性质解决有关问题.
【要点梳理】
要点一、平面的基本概念
1.平面的概念:
“平面”是一个只描述而不定义的原始概念,常见的桌面、黑板面、平静的水面等都给我们以平面的形象.几何里的平面就是从这些物体中抽象出来的,但是,几何里的平面是无限延展的.
要点诠释:
(1)“平面”是平的(这是区别“平面”与“曲面”的依据);
(2) “平面”无厚薄之分;
(3)“平面”无边界,它可以向四周无限延展,这是区别“平面”与“平面图形”的依据.
2.平面的画法:
通常画平行四边形表示平面.
要点诠释:
(1)表示平面的平行四边形,通常把它的锐角画成,横边长是其邻边的两倍;
(2)两个相交平面的画法:当一个平面的一部分被另一个平面遮住时,把被遮住的部分的线段画为虚线或者不画;
3.平面的表示法:
(1)用一个希腊字母表示一个平面,如平面、平面、平面等;
(2)用表示平面的平行四边形的四个字母表示,如平面;
(3)用表示平面的平行四边形的相对两个顶点的两个字母表示,如平面或者平面;
4.点、直线、平面的位置关系:
(1)点A在直线a上,记作;点A在直线a外,记作;
(2)点A在平面上,记作;点A在平面外,记作;
(3)直线在平面内,记作;直线不在平面内,记作.
要点二、平面的基本性质
平面的基本性质即书中的三个公理,它们是研究立体几何的基本理论基础.
1.公理1:
(1)文字语言表述:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内;
(2)符号语言表述:,,,;
(3)图形语言表述:
要点诠释:
公理1是判断直线在平面内的依据.证明一条直线在某一平面内,只需证明这条直线上有两个不同的点在该平面内.“直线在平面内”是指“直线上的所有点都在平面内”.
2.公理2:
(1)文字语言表述:过不在一条直线上的三点,有且只有一个平面;
(2)符号语言表述:、、三点不共线有且只有一个平面,使得,,;
(3)图形语言表述:
要点诠释:
公理2的作用是确定平面,是把空间问题化归成平面问题的重要依据.它还可用来证明“两个平面重合”.特别要注意公理2中“不在一条直线上的三点”这一条件.
“有且只有一个”的含义可以分开来理解.“有”是说明“存在”,“只有一个”说明“唯一”,所以“有且只有一个”也可以说成“存在”并且“唯一”,与确定同义.
(4)公理2的推论:
①过一条直线和直线外一点,有且只有一个平面;
②过两条相交直线,有且只有一个平面;
③过两条平行直线,有且只有一个平面.
(5)作用:确定一个平面的依据.
3.公理3:
(1)文字语言表述:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线;
(2)符号语言表述:且;
(3)图形语言表述:
要点诠释:
公理3的作用是判定两个平面相交及证明点在直线上的依据.
要点三、证明点线共面
所谓点线共面问题就是指证明一些点或直线在同一个平面内的问题.
1.证明点线共面的主要依据:
(1)如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内(公理1);②经过不在同一条直线上的三点,有且只有一个平面(公理2及其推论).
2.证明点线共面的常用方法:
(1)纳入平面法:先确定一个平面,再证明有关点、线在此平面内;(2)辅助平面法:先证明有关的点、线确定平面α,再证明其余元素确定平面β,最后证明平面a、β重合;(3)反证法.
3.具体操作方法:
(1)证明几点共面的问题可先取三点(不共线的三点)确定一个平面,再证明其余各点都在这个平面内;
(2)证明空间几条直线共面问题可先取两条(相交或平行)直线确定一个平面,再证明其余直线均在这个平面内.
要点四、证明三点共线问题
所谓点共线问题就是证明三个或三个以上的点在同—条直线上.
1.证明三点共线的依据是公理3:如果两个不重合的平面有一个公共点,那么它们还有其他的公共点,且所有这些公共点的集合是一条过这个公共点的直线.也就说一个点若是两个平面的公共点,则这个点在这两个平面的交线上.
对于这个公理应进一步理解下面三点:①如果两个相交平面有两个公共点,那么过这两点的直线就是它们的交线;②如果两个相交平面有三个公共点,那么这三点共线;③如果两个平面相交,那么一个平面内的直线和另一个平面的交点必在这两个平面的交线上.
2.证明三点共线的常用方法
方法1:首先找出两个平面,然后证明这三点都是这两个平面的公共点.根据公理3知,这些点都在交线上.
方法2:选择其中两点确定一条直线,然后证明另一点也在其上.
要点五、证明三线共点问题
所谓线共点问题就是证明三条或三条以上的直线交于一点.
1.证明三线共点的依据是公理3.
2.证明三线共点的思路:先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.
【经典例题】
类型一、平面的概念及其表示
例1.下面的说法中正确的是( ).
A.平行四边形是一个平面
B.任何一个平面图形都是一个平面
C.平静的太平洋面就是一个平面
D.圆和平行四边形都可以表示平面
【答案】D
【解析】 利用平面的基本特征以及平面与平面图形的区别进行判断.
A不正确.我们用平行四边形来表示平面,但不能说平行四边形是一个平面.平行四边形仅是平面上四条线段构成的图形,它是不能无限延展的.
B不正确,平面图形和平面是完全不同的两个概念,平面图形是有大小的,它是不可以无限延展的.
C不正确,太平洋再大也会有边际,也不可能是绝对平面.
D正确.在需要时,除用平行四边形表示平面外,还能用三角形、梯形、圆等来表示平面.
【总结升华】 平面与平面图形既有区别又有联系.平面没有角度、绝对平展、无边界,是一种理想的图形.平面可以用三角形、正方形、梯形、圆等平面图形来表示.但平面图形如三角形、正方形、梯形等,它们是有大小之分的,不能说三角形、正方形、梯形等是平面.
举一反三:
【变式1】下列命题:
(1)书桌面是平面;(2)8个平面重叠起来要比6个平面重叠起来厚;(3)有一个平面的长是50 m,宽是20 m;(4)平面是绝对的平、无厚度、可以无限延展的抽象的数学概念.
其中正确命题的个数为( ).
A.1 B.2 C.3 D.4
【答案】A
例2.平面内的直线a、b相交于点P,用符号语言概述为“,且P∈ ”,是否正确?
【答案】不正确
【解析】不正确.应表示为:,,且a∩b=P.
相交于点P的直线a、b都在平面内,也可以说,平面经过相交于点P的直线a、b.题中的符号语言只描述了直线a、b交于点P,点P在平面内,而没有描述直线a、b也都在平面内,下图也是题中的符号语言所表示的情形.
【总结升华】用符号语言来叙述时,必须交代清楚所有元素的位置关系,不能有半点遗漏.
立体几何中的三种语言(文字语言、符号语言、图形语言组成立体几何语言,我们强须准确地把握它们.其中文字语言比较自然、生动,能将问题研究的对象的含义更明确地叙述出来.图形语言给人以清晰的视觉形象,有助于空间想象力的培养;而符号语言更精练、简洁.三种语言的互译有助于我们在更广阔的思维领域里寻找解决问题的途径,有利于对思维广阔性的培养.
举一反三:
【变式1】指出图中的图形画法是否正确,如不正确,请改正.
(1)如图1,直线a在平面α内.
(2)如图2,直线a和平面α相交.
(3)如图3,直线a和平面α平行.
【答案】详见解析
【解析】(1)(2)(3)的图形画法都不正确.正确画法如下图:
(1)直线a在平面α内:
(2)直线a与平面α相交:
(3)直线a与平面α平行:
类型二、平面的确定
例3.判断下列说法是否正确,并说明理由:
(1)一点和一条直线确定一个平面;
(2)经过一点的两条直线确定一个平面:
(3)两两相交的三条直线确定一个平面;
(4)首尾依次相接的4条线段在同一平面内.
【答案】不正确 正确 不正确 不正确
【解析】(1)不正确.如果点在直线上,可以确定无数个平面;如果点不在直线上,在已知直线上任取两个不同的点,由公理2知,有且只有一个平面,或直接由公理2的推论1知,有且只有一个平面.
(2)正确.经过同一点的两条直线是相交直线,由公理2的推论2知,有且只有一个平面.
(3)不正确.3条直线可能交于同一点,也可能有三个不同交点,如下图(1)、(2)所示.前者,由公理2的推论2知.可以确定1个或3个平面;后者,由公理2的推论2及公理1知,能确定一个平面.
(4)不正确.四边形中三点可确定一个平面,而第4点不一定在此平面内,如上图(3),因此这4条线段不一定在同一平面内.
【总结升华】公理2及其3个推论都是确定平面的依据,对涉及这方面的应用问题,务必分清它们的条件.立体几何研究的对象是空间点、线、面的位置关系问题,要有一定的空间想象能力.对于问题中的点、线,要注意它们各种不同的位置关系,以及由此产生的不同结果.
举一反三:
【变式1】正方体的八个顶点一共可以确定 个平面.
【答案】20
例4.三个互不重合的平面,能把空间分成n部分,则n的所有可能值为______________.
【思路点拨】将互不重合的三个平面的位置关系分为:三个平面互相平行;三个平面有两个平行,第三个平面与其它两个平面相交;三个平面交于一线;三个平面两两相交且三条交线平行;三个平面两两相交且三条交线交于一点;五种情况并分别讨论,即可得到答案.
【答案】4,6,7,8
【解析】若三个平面互相平行,则可将空间分为4部分;
若三个平面有两个平行,第三个平面与其它两个平面相交,则可将空间分为6部分;
若三个平面交于一线,则可将空间分为6部分;
若三个平面两两相交且三条交线平行(联想三棱柱三个侧面的关系),则可将空间分为7部分;
若三个平面两两相交且三条交线交于一点(联想墙角三个墙面的关系),则可将空间分为8部分;
故n等于4,6,7或8
类型三、平面的基本性质的应用
例5.如右图,在正方体ABCD-A1B1C1D1中,判断下列命题是否正确,并说明理由.
(1)直线AC1在平面CC1B1B内;
(2)设正方形ABCD与正方形A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
(3)由点A、D、C可以确定一个平面;
(4)由点A、C1、B1确定的平面为ADC1B1;
(5)由点A、C1、B1确定的平面与由点A、C1、D确定的平面是同一个平面.
【解析】(1)错误.因为点A平面CC1B1B,所以AC1不在平面CC1B1B内.
(2)正确.因为点O∈直线AC,直线AC平面AA1C1C,所以点O∈平面AA1C1C.同理,点O1∈平面AA1C1C,所以直线OO1平面AA1C1C.同理,直线OO1平面BB1D1D.故OO1为平面AA1C1C与平面BB1D1D的交线.
(3)错误.因为点A、O、C在同一直线上,故不能确定—个平面
(4)正确.因为点A、C1、B1不共线,故可确定一个平面,又AD∥B1C1,所以点D∈平面AB1C1,故由点A、C1、B1确定的平面为ADC1B1.
(5)正确.因为点A、C1、B1确定的平面为平面ADC1B1,而由点A、C1、D确定的平面也是平面ADC1B1,故它们确定的是同一个平面.
【总结升华】正确地运用三个公理和有关概念的推理是解决此类题目的依据.
例6.已知直线a∥b,直线与a,b都相交,求证:过a,b,有且只有一个平面.
证明 证法一:如下图所示.由已知a∥b,所以过a,b有且只有一个平面.设,,∴A∈,B∈,且A∈,B∈,∴.即过a,b,有且只有一个平面.
证法二:由已知可设,.
∵,过与a有且只有一个平面.
∵a∥b,∴过a,b有且只有一个平面,
∴B∈,B∈,,.
又Ba,∴平面与重合.
即a∥b,.,过a,b,有且只有一个平面.
【总结升华】在证明多线共面时,可用下面的两种方法来证明:
(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平面内.确定一个平面的方法:①直线和直线外一点确定一个平面;②两条平行线确定一个平面;③两条相交直线确定一个平面.
(2)重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.
举一反三:
【变式】(1)空间两两相交的四条直线能确定几个平面?
(2)证明空间不共点且两两相交的四条直线在同一平面内.
【答案】(1)1或6;(2)略
【解析】(1)略
(2)分两种情形,有三条交于一个点,没有三条交于一个点.
已知:直线AB、BC、CD、DA两两相交,且不过同一点.
求证:直线AB、BC、CD、DA 共面.
证明:如图(左), AB、BC、CD、DA两两相交,且无三条直线相交于一点.
设 AD、BC 交于点M,AB、CD交于点N.∴ AB、CD确定一个平面α.
又∵ C∈CD,B∈AB,D∈CD,A∈AB.∴A、B、C、D∈α.
由公理1,知 AD、BC∈α .
故AB、BC、CD、DA 四条直线共面.
如图(右),AB、BC、CD、DA两两相交,且有三直线交于一点D.
∵ AB∩CD=C. ∴ AB、CD确定一个平面β.
又∵ A∈AB,D∈CD,∴A、D∈β,B∈AB,D∈CD,∴ B、D∈β.
∴ AD(β,BD(β(公理1).∴ AB、BC、CD、DA四直线共面.
例7.如下图,已知△ABC的三个顶点都不在平面内,它的三边AB、BC、AC延长后分别交平面 于点P、Q、R.求证:P、Q、R在同一条直线上.
证明 由已知AB的延长线交平面于点P,根据公理3,平面ABC与平面必相交于一条直线,设为L.
∵P∈直线AB,
∴P∈平面ABC.
又AB∩=P, ∴P∈平面,
∴P是平面ABC与平面的公共点.
∵平面ABC∩=,∴P∈,
同理,Q∈,R∈.
∴点P、Q、R在同一条直线上.
【总结升华】多点共线中的这条线一定是两个平面的交线,因此这类问题实际为两平面的相交问题.
举一反三:
【变式1】已知E,F,G,H分别是空间四边形各边AB,AD,BC,CD上的点,且直线EF与GH交于点P.求证:B,D,P在同一直线上.
【解析】
例8.(2017 甘肃天水月考)在正方体中,E为AB的中点,F为的中点,求证:CE,,DA三线共点.
【思路点拨】延长、DA交于P,连结EP,由已知条件得△PAE≌△PAF,从而得到∠PEA+∠AEC=180°,由此能证明CE、、DA三线共点于P.
【答案】略
【解析】延长、DA交于P,连结EP
∵AE=AF,PA=PA,∠PAE=∠PAF=90°,
∴△PAE≌△PAF,
∴∠PFA=∠PEA,
∵∠PEA=,=∠DCE(=∠BCE),
∴∠PEA=∠DCE,
又∵∠DCE+∠AEC=180°,
∴∠PEA+∠AEC=180°,
即点P、E、C共线,
∴CE,,DA三线共点于P.
【总结升华】本题考查三线共点的证明,题时要认真审题,注意空间思维能力的培养.
举一反三:
【变式1】 如下图,已知空间四边形ABCD(即四个点不在同一平面内的四边形)中,E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且.
求证:直线EF、GH、AC相交于一点.
证明:∵E、H分别是边AB、AD的中点,
∴EH∥BD且.
∵F、G分别是边BC、CD上的点,且,
∴FG∥BD且.
故知EH∥FGE且EH≠FG,
即四边形EFGH为梯形,从而EF与GH必相交,设交点为P.
∵P∈EF,EF平面ABC,∴P∈平面ABC.
同理P∈平面ADC.
∵平面ADC∩平面ABC=AC,∴P∈AC.
即EF、GH、AC交于一点P
【巩固练习】
1.“直线经过平面外一点”用符号表示为( )
A. B. C. D.
2.下面图形均表示两个相交平面,其中画法正确的是( )
3.已知平面α与平面β、γ都相交,则这三个平面可能的交线有( )
A.1条或2条 B.2条或3条
C.1条或3条 D.1条或2条或3条
4.下列说法正确的是( )
A.空间四边形的对角线可能相交
B.四个角都是直角的四边形一定是平面图形
C.两两相交的三条直线一定共面
D.在空间的四点,若无三点共线,则这四点一定不共面.
5.空间四点A,B,C,D共面而不共线,那么这四点中( ).
A.必有三点共线 B.必有三点不共线 C.至少有三点共线 D.不可能有三点共线
6.若三个平面把空间分成6个部分,那么这三个平面的位置关系是( )
A. 三个平面共线
B. 有两个平面平行且都与第三个平面相交
C. 三个平面共线,或两个平面平行且都与第三个平面相交
D.三个平面两两相交.
7.把下列符号叙述所对应的图形(如图)的序号填在题后横线上.
(1)Aα,a在平面α内________.
(2)α∩β=a,Pα且Pβ________.
(3)aα,a∩α=A________.
(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O________.
8.在空间四边形中,点分别在上,若直线与相交于点,则点与直线的关系是 .
9.(2017春 江苏启东市期末)若直线l上有两个点在平面α内,则下列说法正确的序号为________
①直线l上至少有一个点在平面α外;
②直线l上有无穷多个点在平面α外;
③直线l上所有点都在平面α内;
④直线l上至多有两个点在平面α内.
10.三个平面把空间分成7部分时它们的交线有 条.
11.画一个正方体ABCD-A1B1C1D1,再画出平面AC D1与平面BD C1的交线,并且说明理由.
12.(2017 安徽蚌埠月考)如图,已知E、F、G、H分别是三棱锥A—ABC的棱AB、BC、CD、DA的中点.
求证:E、F、G、H四点共面
13.若空间中三个平面两两相交于三条直线,这三条直线两两不平行,求证此三条直线必相交于一点.
【答案与解析】
1.C
【解析】 注意点与直线、点与平面之间的关系是元素与集合的关系,直线与平面之间的关系是集合与集合之间的关系.故选C.
2.【答案】D
【解析】 A中图形没有画出两平面的交线;B、C中图形的实、虚线没有按照画法原则去画,也不正确.故选D.
3.【答案】D
【解析】当α过平面β与γ的交线时,这三个平面有1条交线,
当β∥γ时,α与β和γ各有一条交线,共有2条交线.
当β∩γ=b,α∩β=a,α∩γ=c时,有3条交线.
故选D.
4.【答案】B
【解析】 空间四边形的对角线一定不相交,故A不正确;两两相交的三条直线能确定1或3个平面,故C不正确;在空间的四点,若无三点共线,则这四点可能共面也可能不共面,故D不正确.所以只有B正确.
5.【答案】B
【解析】 空间四点A,B,C,D共面而不共线,则至少有一点不在其余点中的两点确定的直线上.如CAB,无论C点在何位置,C,A,B不共线.故选B.
6.【答案】C
【解析】如下图,三个平面相交的截面图是下面两种情况时,把空间分成6个部分.
7.【答案】(1)C (2)D (3)A (4)B
8.【答案】
【解析】由公理3可得。
9.【答案】③
【解析】若直线l上有两个点在平面α内,则直线l在平面α内,
所以直线l上所有点都在平面α内.
所以正确的命题是③.
故答案为:③.
10.【答案】3
【解析】三个平面如图相交时,把空间分成7个部分,所以交线是3条.
11.【解析】如图,为所求.
12.【证明】依题意,EH为△ABD的中位线,
∴EH∥BD,
同理GF∥BD,
∴四边形EFGH为平行四边形,
∴E、F、G、H四点共面.
13.【证明】∵l1在平面β内,l2在平面β内,l1l2,
∴l1∩l2交于一点,记交点为P.
∵P∈l1在平面β内,P∈l2在平面γ内,
∴P∈β∩γ=l3,
∴l1,l2,l3交于一点.
