22.2 第2课时 配方法 课件(13张PPT)
文档属性
| 名称 | 22.2 第2课时 配方法 课件(13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 88.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 10:14:25 | ||
图片预览





文档简介
课件13张PPT。22.2 一元二次方程的解法第2课时 配方法1.掌握用配方法解一元二次方程;(重点)
2.能根据一元二次方程的特征,灵活选择解法. (难点)读诗词解题:
(通过列方程,算出周瑜去世时的年龄)
大江东去浪淘尽,千古风流数人物.
而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?解:设个位数字为x,十位数字为x-3 x2-11x+30=0x2=10(x-3)+x
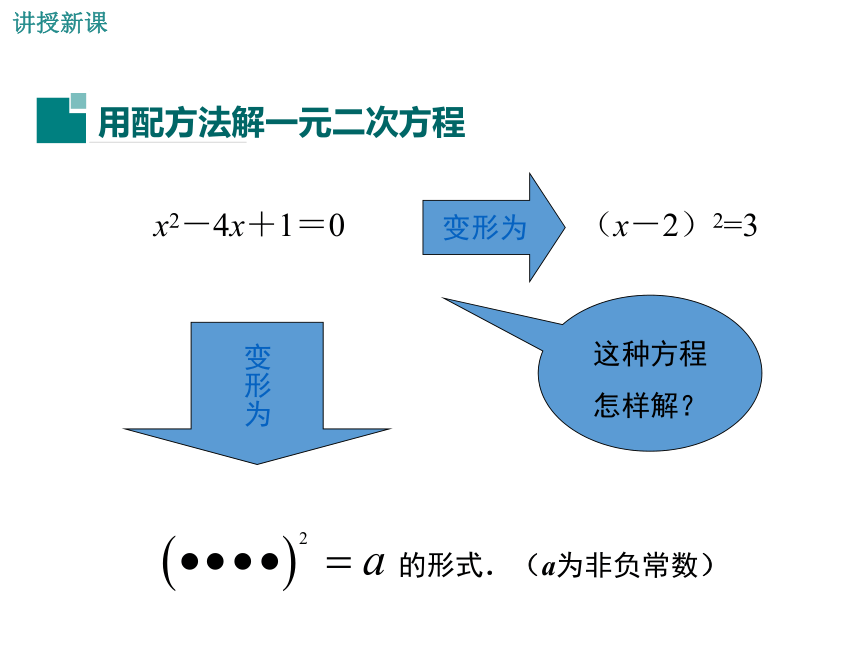
导入新课思考这种方程怎样解?变形为的形式.(a为非负常数)变形为x2-4x+1=0(x-2)2=3讲授新课 像这种先对原一元二次方程配方,使它出现完全平方式后, 再用直接开平方法求解的方法叫做配方法.(1)x2+8x+ =(x+4)2
(2)x2-4x+ =(x- )2
(3)x2-___x+ 9 =(x- )2 配方时, 等式两边同时加上的是一次项系数一半的平方.166342探究归纳例 用配方法解下列方程:
(1)x2-4x-1=0;
(2)2x2-3x-1=0.典例精析用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.(2) -x2+4x-3=0(1) x2+12x =-9 1.用配方法解下列方程:当堂练习解:(1) 两边同时加上36,得x2+12x+36 =-9+36,
配方得(x+6)2=27,解得
(2)原方程可变形为x2-4x+3=0,配方得(x-1)(x-3)=0,
x1=1,x2=3.2.用配方法说明:不论k取何实数,多项式k2-3k+5的值必
定大于零. 3.先用配方法解下列方程:
(1) x2-2x-1=0; (2) x2-2x+4=0;
(3) x2-2x+1=0;
然后回答下列问题:
(4)你在求解过程中遇到什么问题?你是怎样处理所遇到的问题的?
(5)对于形如x2+px+q=0这样的方程,在什么条件下才有实数根?解:(1) 左右两边同时加2,得x2-2x+1=2,
配方得(x-1)2=2,解得
(2)左右两边同时减去3,得x2-2x+1=-3,
配方得(x-1)2=-3,很明显此方程无解;
(3)原方程配方得(x-1)2=0,解得x=1;
(4)略;
(5) 1.一般地,对于形如x2=a(a≥0)的方程,根据平方根的定义,可解得 ,这种解一元二次方程的方法叫做直接开平方法. 2.像这种先对原一元二次方程配方,使它出现完全平方式后, 再用直接开平方法求解的方法叫做配方法. 注意:配方时, 等式两边同时加上的是一次项系数一半的平方.课堂小结用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.
2.能根据一元二次方程的特征,灵活选择解法. (难点)读诗词解题:
(通过列方程,算出周瑜去世时的年龄)
大江东去浪淘尽,千古风流数人物.
而立之年督东吴,早逝英年两位数.
十位恰小个位三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?解:设个位数字为x,十位数字为x-3 x2-11x+30=0x2=10(x-3)+x
导入新课思考这种方程怎样解?变形为的形式.(a为非负常数)变形为x2-4x+1=0(x-2)2=3讲授新课 像这种先对原一元二次方程配方,使它出现完全平方式后, 再用直接开平方法求解的方法叫做配方法.(1)x2+8x+ =(x+4)2
(2)x2-4x+ =(x- )2
(3)x2-___x+ 9 =(x- )2 配方时, 等式两边同时加上的是一次项系数一半的平方.166342探究归纳例 用配方法解下列方程:
(1)x2-4x-1=0;
(2)2x2-3x-1=0.典例精析用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.(2) -x2+4x-3=0(1) x2+12x =-9 1.用配方法解下列方程:当堂练习解:(1) 两边同时加上36,得x2+12x+36 =-9+36,
配方得(x+6)2=27,解得
(2)原方程可变形为x2-4x+3=0,配方得(x-1)(x-3)=0,
x1=1,x2=3.2.用配方法说明:不论k取何实数,多项式k2-3k+5的值必
定大于零. 3.先用配方法解下列方程:
(1) x2-2x-1=0; (2) x2-2x+4=0;
(3) x2-2x+1=0;
然后回答下列问题:
(4)你在求解过程中遇到什么问题?你是怎样处理所遇到的问题的?
(5)对于形如x2+px+q=0这样的方程,在什么条件下才有实数根?解:(1) 左右两边同时加2,得x2-2x+1=2,
配方得(x-1)2=2,解得
(2)左右两边同时减去3,得x2-2x+1=-3,
配方得(x-1)2=-3,很明显此方程无解;
(3)原方程配方得(x-1)2=0,解得x=1;
(4)略;
(5) 1.一般地,对于形如x2=a(a≥0)的方程,根据平方根的定义,可解得 ,这种解一元二次方程的方法叫做直接开平方法. 2.像这种先对原一元二次方程配方,使它出现完全平方式后, 再用直接开平方法求解的方法叫做配方法. 注意:配方时, 等式两边同时加上的是一次项系数一半的平方.课堂小结用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.
