21.2 第2课时 二次根式的除法 课件(18张PPT)
文档属性
| 名称 | 21.2 第2课时 二次根式的除法 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 286.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 10:14:25 | ||
图片预览






文档简介
课件18张PPT。21.2 二次根式的乘除第2课时 二次根式的除法学习目标1.掌握二次根式的除法法则及商的算术平方根的性质;
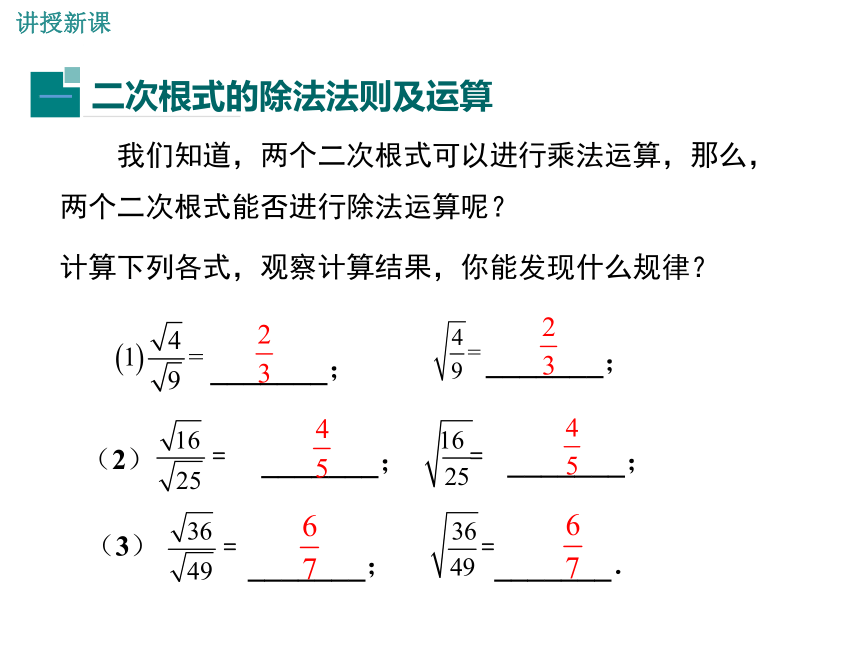
(重点)2.会利用除法法则进行二次根式的运算.(难点)1.二次根式的两个基本性质:=a(a ≥ 0)=∣a∣a (a≥ 0)-a (a<0)=导入新课观察与思考2.二次根式的乘法:算术平方根的积等于各个被开方数积的算术平方根.积的算术平方根等于各因式的算术平方根的积.3.二次根式乘法运算规律公式(a≥0,b≥0)关键:将被开方数因式分解或因数分解,使被开方数出现“完全平方数”或“偶次方因式”.如何化简二次根式(2) (3) _______; _______;_______;_______;_______;_______.计算下列各式,观察计算结果,你能发现什么规律?讲授新课 我们知道,两个二次根式可以进行乘法运算,那么,两个二次根式能否进行除法运算呢? 归纳一般地,二次根式的除法法则(a≥0,b>0) 两个二次根式相除,等于把被开方数相除,作为商的被开方数.思考:等式中的a和b有没有条件的限制?解:典例精析例1 计算:公式的逆用注意:(1) 这里的被开方数是一个整式(可以是多项式,也可以是单项式). (2) 注意被开方数的取值范围.1.与积的算术平方根的性质比较:共同点:一个根号变成两个根号.区别:取值范围不同.商的算术平方根:2.理解和记忆商的算术平方根要注意的问题:比较,得出结论解:提示:(1)要进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简;(2)有理化因式确定方法.如 有理化因式是它本身, 的有理化因式是 .这种方法有的地方称之为分母有理化,即把分母中的根号化去的过程.例2 化简解: 观察上面各数并思考:
(1)你觉得这些数能否再化简,它们已经是最简二次根式了吗?
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条件就可以说它是最简二次根式了? 可以发现这些式子有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式. 简记为:分母无根号,根号无分母解: 解题支招:为了能迅速准确地把二次根式化成最简二次根式,需要熟记1~100以内非二次根式的化简.
如 等.典例精析1.化简:2.把下列各式分母有理化:当堂练习1. 利用商的算术平方根的性质化简二次根式.2. 二次根式的除法有两种常用方法:(1)利用公式:(2)把除法先写成分式的形式,再进行分母有理化运算.
课堂小结3.最简二次根式的概念 被开方数不含分母;
被开方数中不含能开得尽方的因数或因式.4.如何化去分母中的根号,请举例说明.可以用二次根式的性质,乘除运算法则及分数基本性质化去分母中的根号.5.把一个二次根式化为最简二次根式的依据是什么? 把一个二次根式化为最简二次根式的依据是二次根式的基本性质,二次根式的乘除运算,分数基本性质.
(重点)2.会利用除法法则进行二次根式的运算.(难点)1.二次根式的两个基本性质:=a(a ≥ 0)=∣a∣a (a≥ 0)-a (a<0)=导入新课观察与思考2.二次根式的乘法:算术平方根的积等于各个被开方数积的算术平方根.积的算术平方根等于各因式的算术平方根的积.3.二次根式乘法运算规律公式(a≥0,b≥0)关键:将被开方数因式分解或因数分解,使被开方数出现“完全平方数”或“偶次方因式”.如何化简二次根式(2) (3) _______; _______;_______;_______;_______;_______.计算下列各式,观察计算结果,你能发现什么规律?讲授新课 我们知道,两个二次根式可以进行乘法运算,那么,两个二次根式能否进行除法运算呢? 归纳一般地,二次根式的除法法则(a≥0,b>0) 两个二次根式相除,等于把被开方数相除,作为商的被开方数.思考:等式中的a和b有没有条件的限制?解:典例精析例1 计算:公式的逆用注意:(1) 这里的被开方数是一个整式(可以是多项式,也可以是单项式). (2) 注意被开方数的取值范围.1.与积的算术平方根的性质比较:共同点:一个根号变成两个根号.区别:取值范围不同.商的算术平方根:2.理解和记忆商的算术平方根要注意的问题:比较,得出结论解:提示:(1)要进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简;(2)有理化因式确定方法.如 有理化因式是它本身, 的有理化因式是 .这种方法有的地方称之为分母有理化,即把分母中的根号化去的过程.例2 化简解: 观察上面各数并思考:
(1)你觉得这些数能否再化简,它们已经是最简二次根式了吗?
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条件就可以说它是最简二次根式了? 可以发现这些式子有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式. 简记为:分母无根号,根号无分母解: 解题支招:为了能迅速准确地把二次根式化成最简二次根式,需要熟记1~100以内非二次根式的化简.
如 等.典例精析1.化简:2.把下列各式分母有理化:当堂练习1. 利用商的算术平方根的性质化简二次根式.2. 二次根式的除法有两种常用方法:(1)利用公式:(2)把除法先写成分式的形式,再进行分母有理化运算.
课堂小结3.最简二次根式的概念 被开方数不含分母;
被开方数中不含能开得尽方的因数或因式.4.如何化去分母中的根号,请举例说明.可以用二次根式的性质,乘除运算法则及分数基本性质化去分母中的根号.5.把一个二次根式化为最简二次根式的依据是什么? 把一个二次根式化为最简二次根式的依据是二次根式的基本性质,二次根式的乘除运算,分数基本性质.
