江苏省南京市六校联合体2018-2019学年高一下学期期末联考试题 数学 Word版
文档属性
| 名称 | 江苏省南京市六校联合体2018-2019学年高一下学期期末联考试题 数学 Word版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 18:15:23 | ||
图片预览


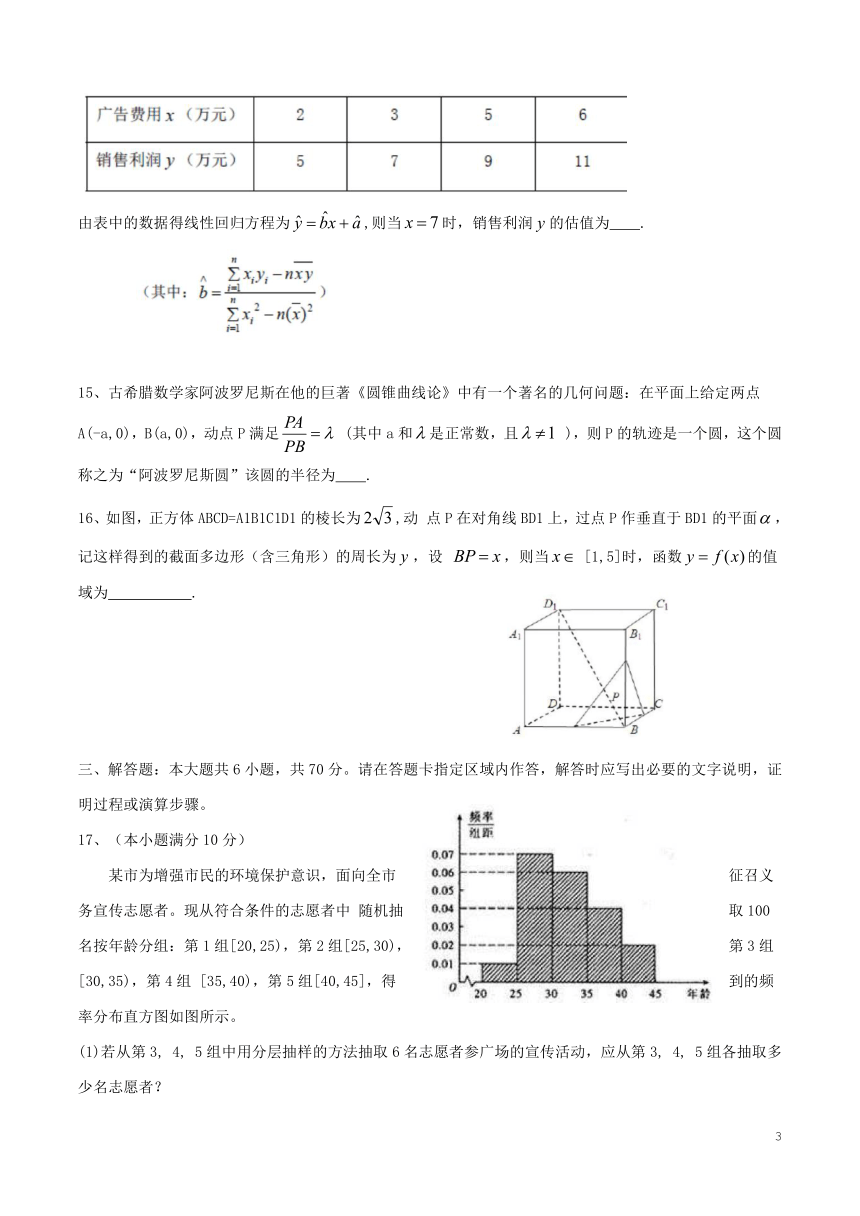


文档简介
南京市六校联合体2018级高一第二学期期末联考
数学试题
一、选择题:本大题共12小题,每题5分,共60分。请把答案填写在答题卞相应位置上。
1、已知圆,圆,则圆与圆 的
位置关系是
A.相离 B.相交 C.外切 D.内切
2、计算的值为
A. B. C. D.
3、在空间直角坐标系中,点P(3,4,5)关于z轴对称的点的坐标为
A. (-3,-4,5) B. (3,-4,5) C. (3,-4,-5) D. (-3,4,5)
4、产能利用率是指实际产出与生产能力的比率,工业产能利用率是衡量工业生产经营状况 的重要指标.下图为国家统计局发布的2015年至2018年第2季度我国工业产能利用率的折线图。
在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2016年第二季度与2015年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2015 年第二季度与2015年第一季度相比较,据上述信息,下列结论中正确的是
A. 2015年第三季度环比有所提高 B. 2016年第一季度同比有所提高
C. 2017年第三季度同比有所提高 D. 2018年第一季度环比有所提高
5、同时抛掷三枚硬币,则抛掷一次时出现两枚正面一枚反面的概率为
A. B. C. D.
6、直线 与 平行,则
A.2 B.2 或3 C.-3 D. -2 或-3
7、己知表示两条不同直线,表示平面,下列说法正确的是
A.若 m // , n //,则 m // n B.若 m 丄,m 丄 n,则 n //
若m丄, n,则m丄n D. 若m // , m丄n,则n丄
8、若圆的圆心在第一象限,则直线—定不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9、在空间四边形ABCD中,AD =2 , BC=,E, F分别是AB, CD的中点,EF = ,则异面直线AD与BC所成角的大小为
A. 150° B. 60° C. 120° D. 30°
10、己知函数和的定义域都是,则它们的图像围成的区域面积是
A. B. C. D.
11、在△ABC中,已知,若△ABC最长边为,则最短边长为
A. B. C. D.
12、已知锐角△ABC中,角A、B、C所对的边分别为a,b,c,若,则的取值范围是
A. B. C. D.
二、填空题:本大题共4小题,每题5分,共20分。请把答案填写在答题卡相应位置上。
13、若直线与圆有公共点,则实数的取值范围是 .
14、某公司调查了商品A的广告投入费用 (万元)与销售利润 (万元)的统计数据,如下表:
由表中的数据得线性回归方程为,则当时,销售利润的估值为 .
15、古希腊数学家阿波罗尼斯在他的巨著《圆锥曲线论》中有一个著名的几何问题:在平面上给定两点A(-a,0),B(a,0),动点P满足 (其中a和是正常数,且 ),则P的轨迹是一个圆,这个圆称之为“阿波罗尼斯圆”该圆的半径为 .
16、如图,正方体ABCD=A1B1C1D1的棱长为,动 点P在对角线BD1上,过点P作垂直于BD1的平面,记这样得到的截面多边形(含三角形)的周长为,设 ,则当 [1,5]时,函数的值域为 .
三、解答题:本大题共6小题,共70分。请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤。
17、(本小题满分10分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者。现从符合条件的志愿者中 随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组 [35,40),第5组[40,45],得到的频率分布直方图如图所示。
(1)若从第3, 4, 5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3, 4, 5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在这6 名志愿者中随机抽取2名志愿者介绍宣传经验,求第5组志愿者有被抽中的概率。
18、(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA丄底面ABCD,E是BC的中点,已知 AB= 2, AD = , PA = 2,求:
(1)直线PC与平面PAD所成角的正切值;
(2)三棱锥P - ABE的体积。
19、(本小题满分12分)
已知△ABC的顶点A(5,1),AC边上的中线BM所在直线方程为,AB边上的高CH所在直线方程为.
(1)求顶点B的坐标;
(2)求直线BC的方程.
20、(本小题满分12分)
如图,直三棱柱ABC-A1B1C1中,点D是棱BC的中点,点D在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
若点M在棱BB1上,且BM=1.
(1)求证:平面CAM丄平面ADF ;
(2)棱AB上是否存在一点E,使得C1E //平面ADF?证
明你的结论。
21、(本小题满分12分)
如图,某住宅小区的平面图呈圆心角为的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD。
(1)已知某人从C沿CD走到D用了 10分钟,从D沿DA走到A用了 6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米)
(2)若该扇形的半径为OA = a,已知某老人散步,从C沿CD走到D,再从D沿DO走到O,试确定C的位置,使老人散步路线最长。
22、(本小题满分12分)
已知△ABC的三个顶点A(-1,0),B(1,0),C(3,2),其外接圆为圆H .
(1)求圆H的方程;
(2)若直线过点C,且被圆H截得的弦长为2,求直线的方程;
(3)对于线段BH上的任意一点P,若在以C为圆心的圆上都存在不同的两点M,N,使得点M是线段PN的中点,求圆C的半径r的取值范围.
PAGE
11
同课章节目录
