23.4 中位线 课件(20张PPT)
文档属性
| 名称 | 23.4 中位线 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 421.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 11:43:03 | ||
图片预览



文档简介
课件20张PPT。23.4 中位线第23章 图形的相似1.理解中位线的概念和性质;(重点)
2.能够利用中位线解决相关问题; (重点、难点)
3.经历三角形中位线的性质定理及重心的推导过程.(难点)问题1 怎样由平行线判定两个三角形相似?
问题2 相似三角形有哪些方面的应用?你会解决下面的问
题吗?
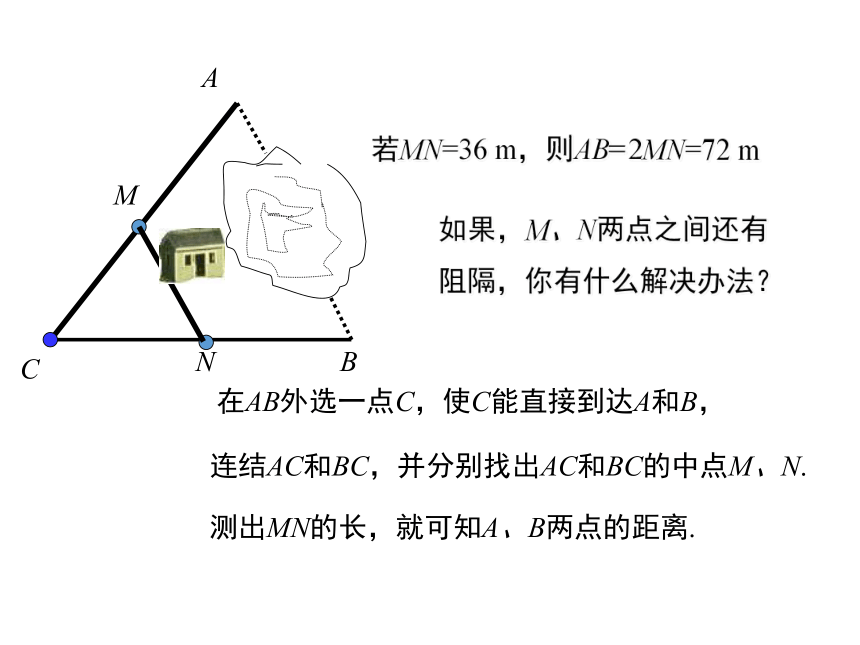
导入新课观察与思考ABC测出MN的长,就可知A、B两点的距离.
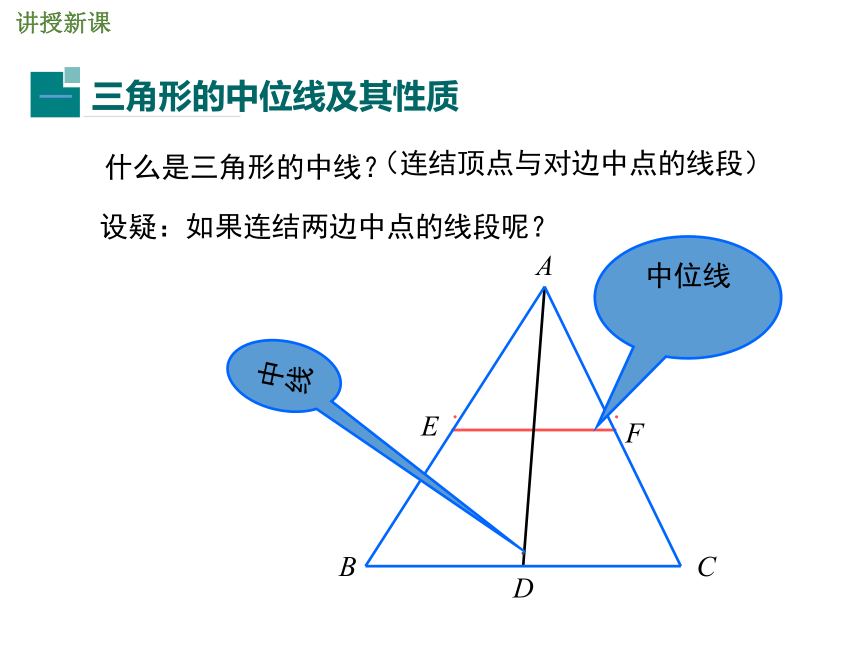
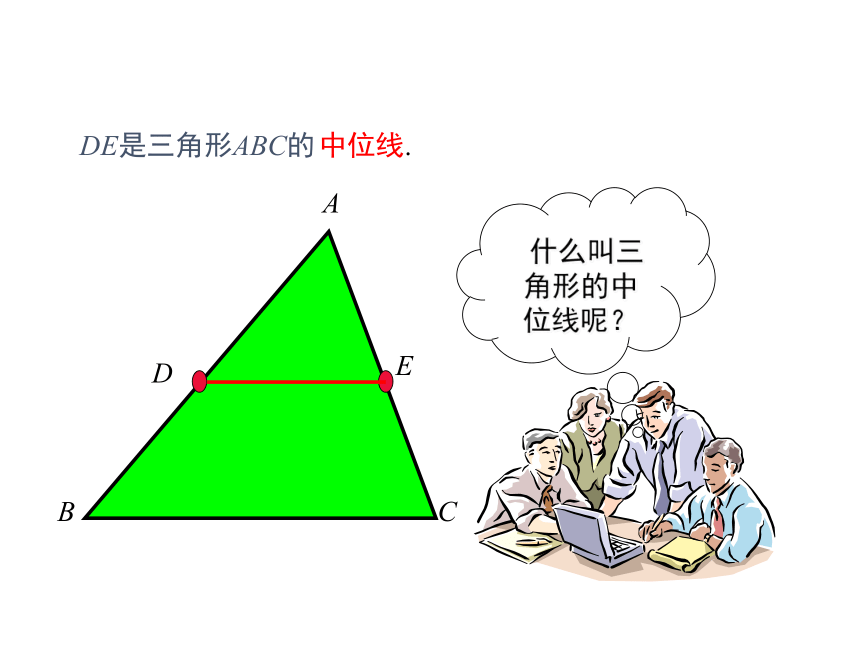
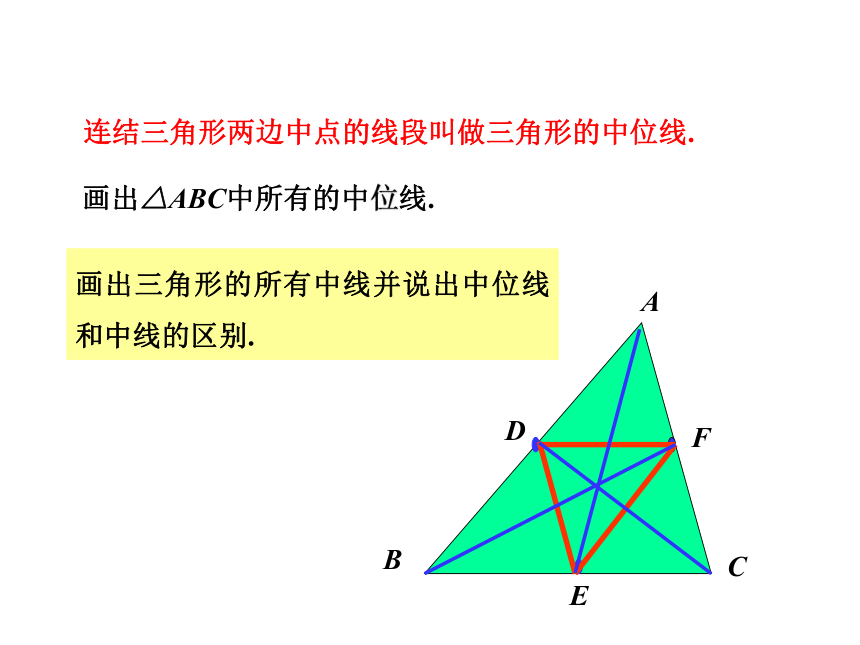
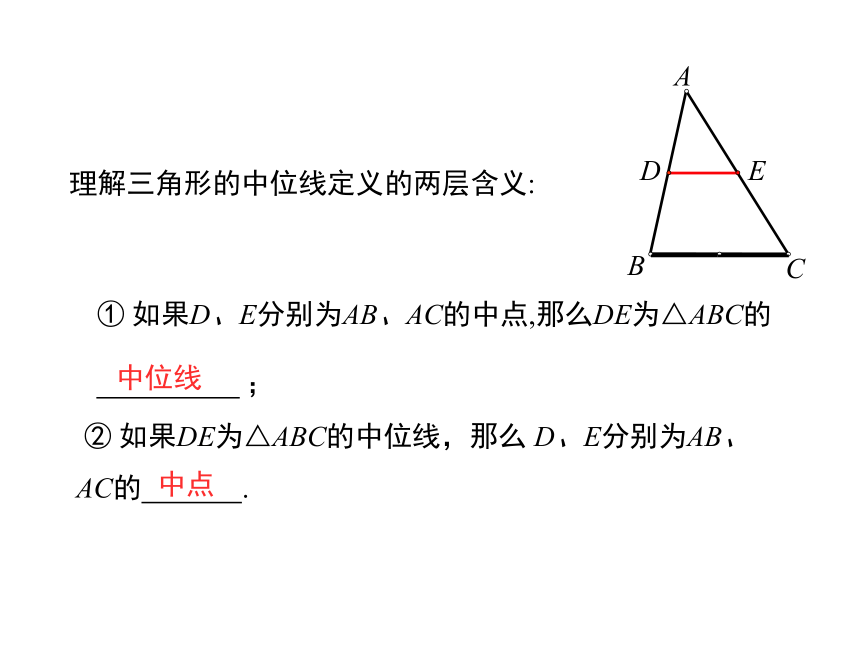
MN在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.若MN=36 m,则AB=2MN=72 m中位线中线什么是三角形的中线?(连结顶点与对边中点的线段)设疑:如果连结两边中点的线段呢?讲授新课DEDE是三角形ABC的中位线. 连结三角形两边中点的线段叫做三角形的中位线.画出三角形的所有中线并说出中位线和中线的区别.DEF理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .① 如果D、E分别为AB、AC的中点,那么DE为△ABC的
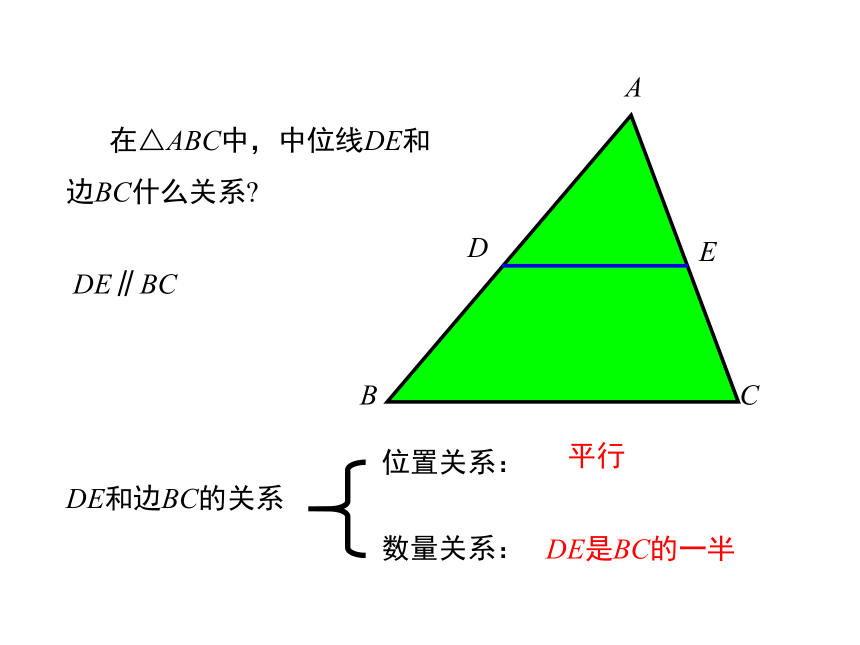
;CBAED中位线中点 在△ABC中,中位线DE和边BC什么关系?DE和边BC的关系数量关系:位置关系:DE∥BCDE平行DE是BC的一半结论:三角形的中位线平行于第三边,并且等于它的一半.如图:在△ABC中,D是AC的中点,E是AB的中点.
则有: DE∥BC,DE= BC.能说出理由吗? 如图,在△ABC中,D是AC的中点,E是AB的中点.
则有: DE∥BC,DE= BC.用不同的方法证明
三角形中位线的性质 三角形的中位线平行于第三边,并且等于它的一半.∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别 是各边中点 AB=6cmAC=8cm,BC=10cm, 则△DEF的周长= cm图1图260412ABCD EBACD EF如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.求证: 证明:连结ED, ∵ D、E分别是边BC、AB的中点,∴ △ACG∽△DEG,如果在上图中,取AC的中点F,假设BF与AD交于G`,如下图,那么我们同理有,
所以有 ,即两图中的点G与G`是重合的.
于是我们有以下结论:
三角形三条边上的中线交于一点,
这个点就是三角形的重心,重心与一边
中点的连线的长是对应中线长的 .
A1.如图:EF是△ABC 的中位线,BC=20,则EF=________;
10 当堂练习2.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是_______________.平行且相等 3.求证:顺次连结四边形四条边的中点所得的四边形是平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= AC.
同理 EF∥AC, EF= AC,
∴HG∥EF ,HG=EF.
∴四边形EFGH是平行四边形.1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于它的一半.3.三角形的中位线性质不仅给出了中位线与第三边的关系,而且给出了它们的数量关系,在三角形中给出一边的中点时,可转化为中位线.课堂小结
2.能够利用中位线解决相关问题; (重点、难点)
3.经历三角形中位线的性质定理及重心的推导过程.(难点)问题1 怎样由平行线判定两个三角形相似?
问题2 相似三角形有哪些方面的应用?你会解决下面的问
题吗?
导入新课观察与思考ABC测出MN的长,就可知A、B两点的距离.
MN在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.若MN=36 m,则AB=2MN=72 m中位线中线什么是三角形的中线?(连结顶点与对边中点的线段)设疑:如果连结两边中点的线段呢?讲授新课DEDE是三角形ABC的中位线. 连结三角形两边中点的线段叫做三角形的中位线.画出三角形的所有中线并说出中位线和中线的区别.DEF理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .① 如果D、E分别为AB、AC的中点,那么DE为△ABC的
;CBAED中位线中点 在△ABC中,中位线DE和边BC什么关系?DE和边BC的关系数量关系:位置关系:DE∥BCDE平行DE是BC的一半结论:三角形的中位线平行于第三边,并且等于它的一半.如图:在△ABC中,D是AC的中点,E是AB的中点.
则有: DE∥BC,DE= BC.能说出理由吗? 如图,在△ABC中,D是AC的中点,E是AB的中点.
则有: DE∥BC,DE= BC.用不同的方法证明
三角形中位线的性质 三角形的中位线平行于第三边,并且等于它的一半.∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别 是各边中点 AB=6cmAC=8cm,BC=10cm, 则△DEF的周长= cm图1图260412ABCD EBACD EF如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.求证: 证明:连结ED, ∵ D、E分别是边BC、AB的中点,∴ △ACG∽△DEG,如果在上图中,取AC的中点F,假设BF与AD交于G`,如下图,那么我们同理有,
所以有 ,即两图中的点G与G`是重合的.
于是我们有以下结论:
三角形三条边上的中线交于一点,
这个点就是三角形的重心,重心与一边
中点的连线的长是对应中线长的 .
A1.如图:EF是△ABC 的中位线,BC=20,则EF=________;
10 当堂练习2.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是_______________.平行且相等 3.求证:顺次连结四边形四条边的中点所得的四边形是平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= AC.
同理 EF∥AC, EF= AC,
∴HG∥EF ,HG=EF.
∴四边形EFGH是平行四边形.1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于它的一半.3.三角形的中位线性质不仅给出了中位线与第三边的关系,而且给出了它们的数量关系,在三角形中给出一边的中点时,可转化为中位线.课堂小结
