23.5 位似图形 课件(16张PPT)
文档属性
| 名称 | 23.5 位似图形 课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 11:43:03 | ||
图片预览




文档简介
课件16张PPT。23.5 位似图形第23章 图形的相似1.了解位似图形及其有关概念;(重点)
2.理解位似图形上任意一组对应点到位似中心的距离之比等于
位似比;(重点)
3.会画位似图形并会利用位似解决一些简单的问题.(难点)问题1 我们学过的图形变换形式有哪些?
问题2 什么叫相似?相似图形有哪些性质?
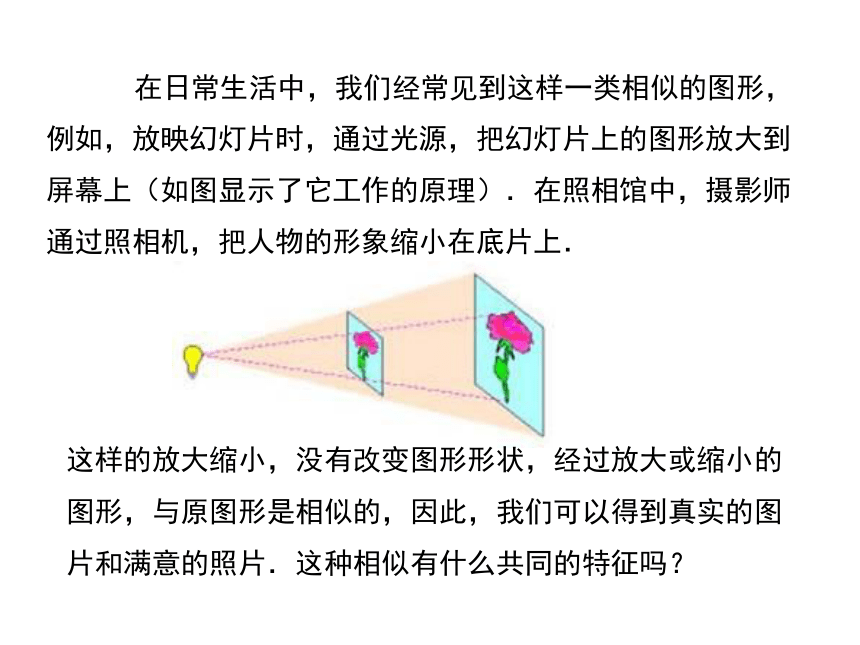
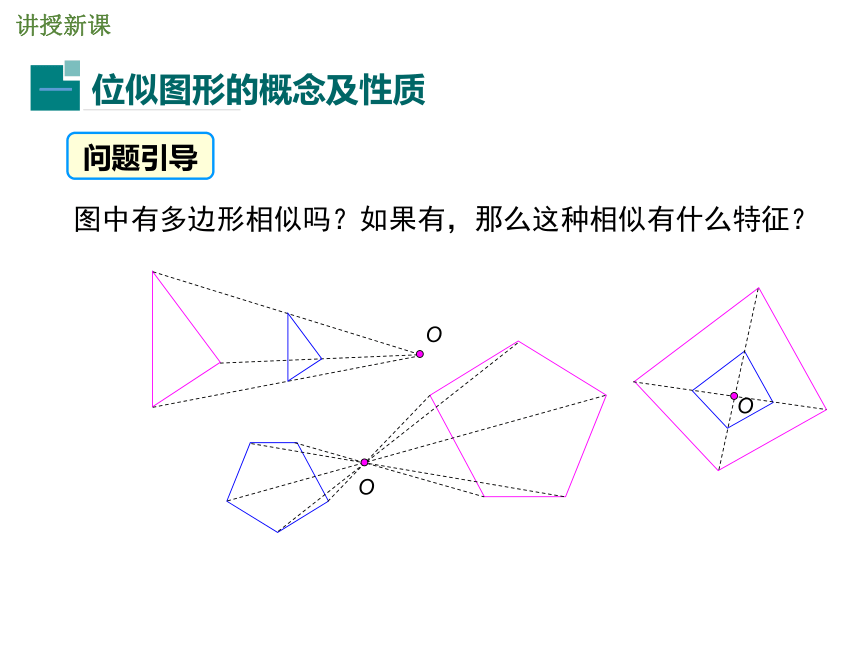
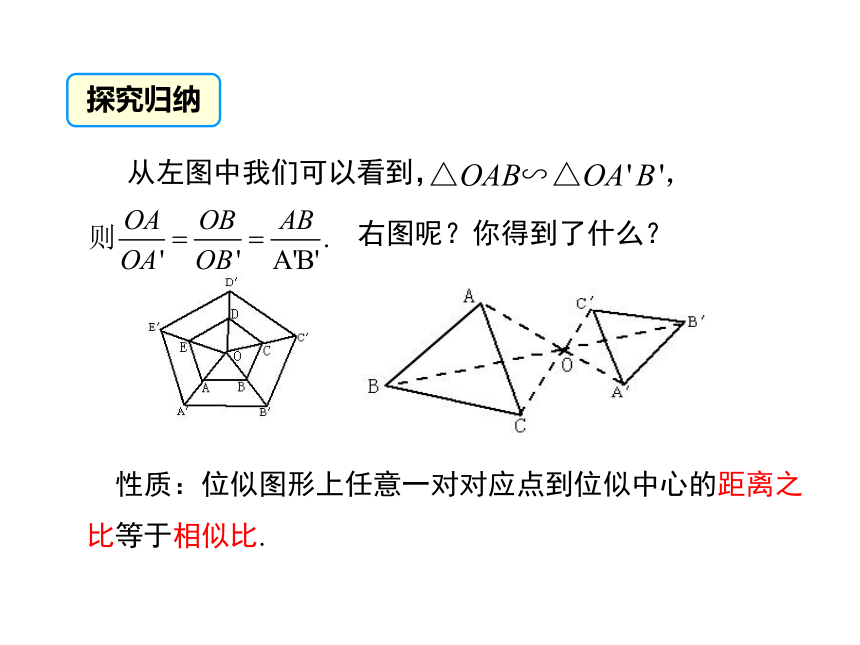
导入新课观察与思考例如,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).在照相馆中,摄影师通过照相机,把人物的形象缩小在底片上.在日常生活中,我们经常见到这样一类相似的图形,这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.这种相似有什么共同的特征吗?图中有多边形相似吗?如果有,那么这种相似有什么特征?OOO讲授新课问题引导 图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这个点叫做位似中心.概念形成: 性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比. 探究归纳从左图中我们可以看到,右图呢?你得到了什么?2) 分别在线段OA、OB、OC、OD上取点A' 、B' 、C' 、D' ,使得
3) 顺次连结点 A' 、B' 、C' 、D' ,所得四边形A' B' C' D' 就是所要求的图形.ODABCA'B'C'D'利用位似,可以将一个图形放大或缩小.1.把四边形ABCD 缩小到原来的1/2.1) 在四边形外任选一点O(如图),对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A ' ,B ' 、C ' 、D ' ,使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.ODABCA'B'C'D'ODABC 2.如图,△ABC,画△A’B’ C‘ ,使△A’ B‘ C’ ∽△ABC,且使相似比为1:4,
要求:(1)位似中心在△ABC的一条边AB上;
(2)以点C为位似中心. BAC(1)位似中心在△ABC的一条边AB上(2)以点C为位似中心假设位似中心点O在AB上,
相似比1:4,点O位置如图
(1)所示o●●A`B`C`●●●A`B`(C`)●●2.利用位似进行作图的关键是确定位似中心和关键点. 3.位似分为内位似和外位似,内位似的位似中心在连结两个对应点的线段上;外位似的位似中心在连结两个对应点的线段之外.1.画位似图形的一般步骤:1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形.归纳1.如图,△OAB 和△OCD是位似图形,AB与CD平行吗?为什么?解:AB∥CD.∵△OAB与△OCD是位似图形,∴△OAB ∽△OCD,∴∠OAB=∠C,∴AB∥CD.当堂练习2. 如图,以O为位似中心,将△ABC放大为原来的两倍.OABC解:①作射线OA 、OB 、 OC ,②分别在OA、OB 、OC 上取点A' 、B' 、C' 使得③顺次连结A' 、B' 、C' 就是所要求图形.A' B' C' 3.画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A`B`C`D`E`.DB1. 位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行或者在一条直线上,像这样的两个图形叫做位似图形,这个点叫做位似中心.
2.位似图形的性质:
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或
相似比;
(4)对应线段平行或者在一条直线上. 课堂小结
2.理解位似图形上任意一组对应点到位似中心的距离之比等于
位似比;(重点)
3.会画位似图形并会利用位似解决一些简单的问题.(难点)问题1 我们学过的图形变换形式有哪些?
问题2 什么叫相似?相似图形有哪些性质?
导入新课观察与思考例如,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).在照相馆中,摄影师通过照相机,把人物的形象缩小在底片上.在日常生活中,我们经常见到这样一类相似的图形,这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.这种相似有什么共同的特征吗?图中有多边形相似吗?如果有,那么这种相似有什么特征?OOO讲授新课问题引导 图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这个点叫做位似中心.概念形成: 性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比. 探究归纳从左图中我们可以看到,右图呢?你得到了什么?2) 分别在线段OA、OB、OC、OD上取点A' 、B' 、C' 、D' ,使得
3) 顺次连结点 A' 、B' 、C' 、D' ,所得四边形A' B' C' D' 就是所要求的图形.ODABCA'B'C'D'利用位似,可以将一个图形放大或缩小.1.把四边形ABCD 缩小到原来的1/2.1) 在四边形外任选一点O(如图),对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A ' ,B ' 、C ' 、D ' ,使得 呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.ODABCA'B'C'D'ODABC 2.如图,△ABC,画△A’B’ C‘ ,使△A’ B‘ C’ ∽△ABC,且使相似比为1:4,
要求:(1)位似中心在△ABC的一条边AB上;
(2)以点C为位似中心. BAC(1)位似中心在△ABC的一条边AB上(2)以点C为位似中心假设位似中心点O在AB上,
相似比1:4,点O位置如图
(1)所示o●●A`B`C`●●●A`B`(C`)●●2.利用位似进行作图的关键是确定位似中心和关键点. 3.位似分为内位似和外位似,内位似的位似中心在连结两个对应点的线段上;外位似的位似中心在连结两个对应点的线段之外.1.画位似图形的一般步骤:1)确定位似中心;
2)分别连接并延长位似中心和能代表原图的关键点;
3)根据相似比,确定能代表所作的位似图形的关键点;
4)顺次连接上述各点,得到放大或缩小的图形.归纳1.如图,△OAB 和△OCD是位似图形,AB与CD平行吗?为什么?解:AB∥CD.∵△OAB与△OCD是位似图形,∴△OAB ∽△OCD,∴∠OAB=∠C,∴AB∥CD.当堂练习2. 如图,以O为位似中心,将△ABC放大为原来的两倍.OABC解:①作射线OA 、OB 、 OC ,②分别在OA、OB 、OC 上取点A' 、B' 、C' 使得③顺次连结A' 、B' 、C' 就是所要求图形.A' B' C' 3.画出以O为位似中心,将五边形ABCDE缩小到原来的0.5倍的五边形A`B`C`D`E`.DB1. 位似图形:如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行或者在一条直线上,像这样的两个图形叫做位似图形,这个点叫做位似中心.
2.位似图形的性质:
(1)位似图形一定相似,位似比等于相似比;
(2)位似图形对应点和位似中心在同一条直线上;
(3)任意一对对应点到位似中心的距离之比等于位似比或
相似比;
(4)对应线段平行或者在一条直线上. 课堂小结
