第21章 二次根式 单元复习课件(20张PPT)
文档属性
| 名称 | 第21章 二次根式 单元复习课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 11:55:13 | ||
图片预览

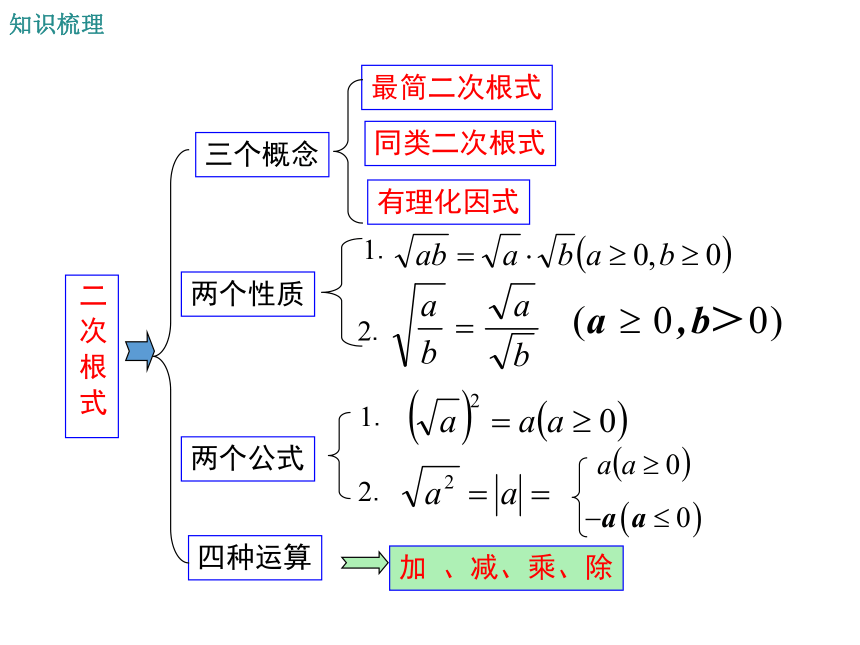







文档简介
课件20张PPT。复习和小结第21章 二次根式知识梳理1.二次根式的概念
一般地,形如____(a≥0)的式子叫做二次根式;
对于二次根式的理解:
①带有根号;②被开方数是非负数,即a≥0.
[易错点] 二次根式中,被开方数一定是非负数,否则就没有意义.2.二次根式的性质
3.最简二次根式
满足下列两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含_______;
(2)被开方数中不含能___________的因数或因式.开得尽方分母4.二次根式的运算
=______(a≥0,b≥0); =____(a≥0,b>0).
二次根式加减时,可以先将二次根式化成_____________,再将________________的二次根式进行合并.被开方数相同 最简二次根式1. 当x _____ 时, 有意义. 3.求下列二次根式中字母的取值范围.解得 - 5≤x<3说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组). ≤3a=4考点分类2. 有意义的条件是 .1.已知: + =0,求 x-y 的值. 2.已知x,y为实数,且 +3(y-2)2 =0,则x-y的值为( )
A.3 B.-3 C.1 D.-1解:由题意,得 x-4=0 且 2x+y=0解得 x=4,y=-8x-y=4-(-8)= 4+ 8 =12D方法技巧
初中阶段主要涉及三种非负数: ≥0, ≥0,a2≥0.如果若干个非负数的和为0,那么这若干个非负数都必为0.即由a≥0,b≥0,c≥0且a+b+c=0,一定得到a=b=c=0,这是求一个方程中含有多个未知数的有效方法之一.CA1.确定二次根式中被开方数所含字母的取值范围
2.二次根式的非负性的应用3.二次根式性质的应用4.二次根式的化简5.二次根式的运算复习归纳C0课后演练 3.若1<x<4,则化简
的结果是_____4.下列各式中,是最简二次根式的是( )3B5.下列各式中那些是二次根式?那些不是?为什么?⑧⑦⑥⑤④①②③a<0-(a2+1)<0(a-1)2≥06.计算:若a为底,b为腰,此时底边上的高为∴三角形的面积为(2)若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的面积.设a、b为实数,且| 2 -a|+ b-2 =0解:若a为腰,b为底,此时底边上的高为∴三角形的面积为7.(2)如图所示,AD⊥DC于D,BC⊥CD于C,ABPDC若点P为线段CD上动点.已知△ABP的一边AB=①则AD=____ BC=____12(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为 8.② 设DP=a,请用含a的代数式表示AP,BP,则AP=_________,BP=__________.③ 当a=1 时,则PA+PB=______,当a=3,则PA+PB=______.④ PA+PB是否存在一个最小值?
一般地,形如____(a≥0)的式子叫做二次根式;
对于二次根式的理解:
①带有根号;②被开方数是非负数,即a≥0.
[易错点] 二次根式中,被开方数一定是非负数,否则就没有意义.2.二次根式的性质
3.最简二次根式
满足下列两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含_______;
(2)被开方数中不含能___________的因数或因式.开得尽方分母4.二次根式的运算
=______(a≥0,b≥0); =____(a≥0,b>0).
二次根式加减时,可以先将二次根式化成_____________,再将________________的二次根式进行合并.被开方数相同 最简二次根式1. 当x _____ 时, 有意义. 3.求下列二次根式中字母的取值范围.解得 - 5≤x<3说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组). ≤3a=4考点分类2. 有意义的条件是 .1.已知: + =0,求 x-y 的值. 2.已知x,y为实数,且 +3(y-2)2 =0,则x-y的值为( )
A.3 B.-3 C.1 D.-1解:由题意,得 x-4=0 且 2x+y=0解得 x=4,y=-8x-y=4-(-8)= 4+ 8 =12D方法技巧
初中阶段主要涉及三种非负数: ≥0, ≥0,a2≥0.如果若干个非负数的和为0,那么这若干个非负数都必为0.即由a≥0,b≥0,c≥0且a+b+c=0,一定得到a=b=c=0,这是求一个方程中含有多个未知数的有效方法之一.CA1.确定二次根式中被开方数所含字母的取值范围
2.二次根式的非负性的应用3.二次根式性质的应用4.二次根式的化简5.二次根式的运算复习归纳C0课后演练 3.若1<x<4,则化简
的结果是_____4.下列各式中,是最简二次根式的是( )3B5.下列各式中那些是二次根式?那些不是?为什么?⑧⑦⑥⑤④①②③a<0-(a2+1)<0(a-1)2≥06.计算:若a为底,b为腰,此时底边上的高为∴三角形的面积为(2)若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的面积.设a、b为实数,且| 2 -a|+ b-2 =0解:若a为腰,b为底,此时底边上的高为∴三角形的面积为7.(2)如图所示,AD⊥DC于D,BC⊥CD于C,ABPDC若点P为线段CD上动点.已知△ABP的一边AB=①则AD=____ BC=____12(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为 8.② 设DP=a,请用含a的代数式表示AP,BP,则AP=_________,BP=__________.③ 当a=1 时,则PA+PB=______,当a=3,则PA+PB=______.④ PA+PB是否存在一个最小值?
