苏科版九年级数学下册第六章图形的相似单元检测试题(无答案)
文档属性
| 名称 | 苏科版九年级数学下册第六章图形的相似单元检测试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 00:00:00 | ||
图片预览




文档简介
苏科版九年级数学下册
第六章 图形的相似 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.中午点,身高为的小冰的影长为,同学小雪此时的影长为,那么小雪的身高为( )
A. B. C. D.
?2.如图,选项中的阴影三角形与相似的为( )
A. B.
C. D.
?3.在比例尺为的地图上,某段路的长度约为厘米,则它的实际长度约为( )
A.米 B.米 C.米 D.米
?4.如图,已知直线,直线和分别与、、相交于点、、和、、.如果,,那么下列各式中,正确的是( )
A. B.
C. D.
?5.如果,那么下列等式中不成立的是( )
A. B.
C. D.
?6.如果点是线段的黄金分割点,那么下列线段比的值不可能是的为( )
A. B. C. D.
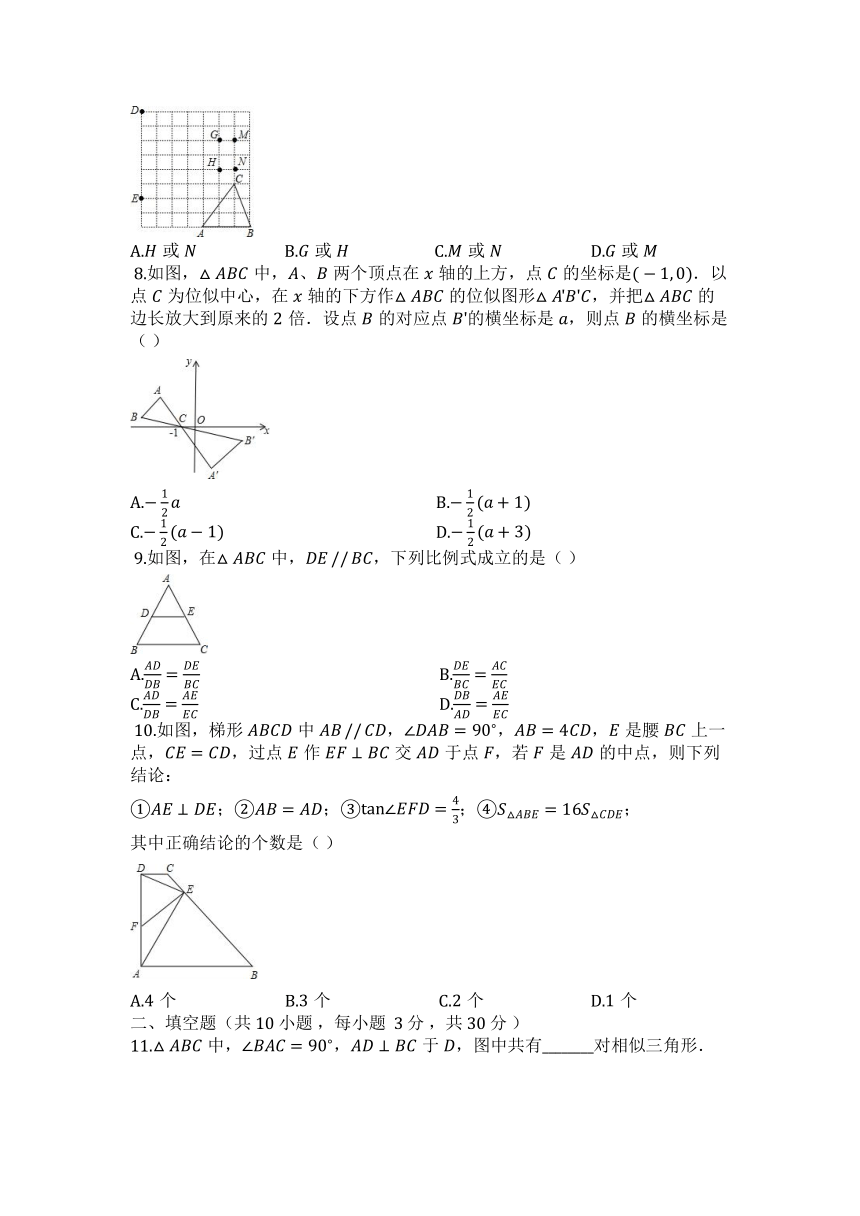
?7.如图,,,,,,,,,都是方格纸中的格点(即小正方形的顶点),要使与相似,则点应是,,,四点中的( )
A.或 B.或 C.或 D.或
?8.如图,中,、两个顶点在轴的上方,点的坐标是.以点为位似中心,在轴的下方作的位似图形,并把的边长放大到原来的倍.设点的对应点的横坐标是,则点的横坐标是( )
A. B.
C. D.
?9.如图,在中,,下列比例式成立的是( )
A. B.
C. D.
?10.如图,梯形中,,,是腰上一点,,过点作交于点,若是的中点,则下列结论:
①;②;③;④;
其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.中,,于,图中共有________对相似三角形.
?12.在和中,如果,,,,那么这两个三角形能否相似的结论是________,理由是________.
?13.两个三角形相似,其中一个三角形的三边分别为、、,另一个三角形的最短边长为,则另外两边之长分别为________和________.
?14.已知两个相似三角形的面积比为,则它们的相似比为________,其中一个周长为,则另一个周长为________.
?15.如图所示,的面积为,取边中点作,,得到四边形,它的面积记作,再取中点,作,得到四边形,它的面积记作,照此规律作下去,________.
?16.已知是轴的正半轴上的点,是由等腰直角三角形以为位似中心变换得到的,如图,已知,,则位似中心点的坐标是________.
?17.如图,已知、、都与垂直,垂足分别是、、,且,,那么的长是________.
?18.由一块底长、高的等腰三角形木板中锯下一块最大的正方形(正方形木板有一边与三角形木板的底边重合).这块正方形木板的面积是________平方米.
?19.如图,在中,,,垂足为,,,则的长为________.
?20.一天,小青在校园内发现一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为米,由此可推断出树高是________米.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,与是位似图形,试说明与是否平行.
?
22.如图,中,,于,,,求.
?
23.在中,,,,将放在如图所示的平面直角坐标系中,且点、点在在轴上,是正半轴上一动点,把绕点逆时针旋转的度数,点旋转后的对应点为.
若时,则点的坐标是________.(直接写出结果)
若旋转后所得三角形和相似时,求此时点的坐标;
是否存在满足条件的点,使直线恰好过点;若存在,求出点的坐标,若不存在,请说明理由.
?
24.如图,和是等腰直角三角形,,点、在的外部,连结,.
求证:;
若将绕点旋转,直线交直线于点,交直线于点.
①如果,,求的值;
②当为等腰直角三角形时,请你直接写出的值.
?
25.已知:如图,在四边形中,,对角线、交于点,点在边上,连接交线段于点,.
求证:;
连接,求证:.
?
26.如图①,已知平面内一点与一直线,如果过点作直线,垂足为,那么垂足叫做点在直线上的射影;如果线段的两个端点和在直线上的射影分别为点和,那么线段叫做线段在直线上的射影.
如图①,已知平面内一点与一直线,如果过点作直线,垂足为,那么垂足叫做点在直线上的射影;如果线段的两个端点和在直线上的射影分别为点和,那么线段叫做线段在直线上的射影.
如图②,、为线段外两点,,,垂足分别为、.
则点在上的射影是________点,点在上的射影是________点,
线段在上的射影是________,线段在上的射影是________;
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
答案
1.A
2.B
3.B
4.C
5.D
6.D
7.C
8.D
9.C
10.A
11.
12.有两组角对应相等的两个三角形相似
13.
14.或
15.
16.
17.
18.
19.
20.
21.解:.
理由:∵与是位似图形,
∴,
∴,
∴.
22.解:如图,∵中,,,
∴.
又∵,,
∴,,
∴,
∴,即.
23.①如图中,当时满足条件,此时易知,,设,
在中,∵,
∴,
∴,
∴,,
由,可得,
∴,,
∴,
∴点坐标.
②如图中,若时,此时,点恰好与点重合,所以,
综上所述,点的坐标是.设点的坐标为,同法可得的坐标是,
设过,,则有,解得
∴,
把,代入,
化简得,解得,(不合题意,舍去),
∴点的坐标是.
24.解:∵
∴,
∴,
在和中,
,
∴,
∴;
①当点在线段上时(如图)
∵,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴.
∴,
当点在线段延长线上时(如图)
∵,
∴,
又∵,
∴,
∴,
∴;
∵,
∴,
∵,
∴
∴;
②如图,
当为等腰直角三角形时,
则,
.
25.证明:∵,
∴.
又∵,
∴.
∴.
∵,
∴.
∴.∵,,
∴.
∴.
又∵,
∴.
∴.
∴.
26.线段线段
第六章 图形的相似 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.中午点,身高为的小冰的影长为,同学小雪此时的影长为,那么小雪的身高为( )
A. B. C. D.
?2.如图,选项中的阴影三角形与相似的为( )
A. B.
C. D.
?3.在比例尺为的地图上,某段路的长度约为厘米,则它的实际长度约为( )
A.米 B.米 C.米 D.米
?4.如图,已知直线,直线和分别与、、相交于点、、和、、.如果,,那么下列各式中,正确的是( )
A. B.
C. D.
?5.如果,那么下列等式中不成立的是( )
A. B.
C. D.
?6.如果点是线段的黄金分割点,那么下列线段比的值不可能是的为( )
A. B. C. D.
?7.如图,,,,,,,,,都是方格纸中的格点(即小正方形的顶点),要使与相似,则点应是,,,四点中的( )
A.或 B.或 C.或 D.或
?8.如图,中,、两个顶点在轴的上方,点的坐标是.以点为位似中心,在轴的下方作的位似图形,并把的边长放大到原来的倍.设点的对应点的横坐标是,则点的横坐标是( )
A. B.
C. D.
?9.如图,在中,,下列比例式成立的是( )
A. B.
C. D.
?10.如图,梯形中,,,是腰上一点,,过点作交于点,若是的中点,则下列结论:
①;②;③;④;
其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.中,,于,图中共有________对相似三角形.
?12.在和中,如果,,,,那么这两个三角形能否相似的结论是________,理由是________.
?13.两个三角形相似,其中一个三角形的三边分别为、、,另一个三角形的最短边长为,则另外两边之长分别为________和________.
?14.已知两个相似三角形的面积比为,则它们的相似比为________,其中一个周长为,则另一个周长为________.
?15.如图所示,的面积为,取边中点作,,得到四边形,它的面积记作,再取中点,作,得到四边形,它的面积记作,照此规律作下去,________.
?16.已知是轴的正半轴上的点,是由等腰直角三角形以为位似中心变换得到的,如图,已知,,则位似中心点的坐标是________.
?17.如图,已知、、都与垂直,垂足分别是、、,且,,那么的长是________.
?18.由一块底长、高的等腰三角形木板中锯下一块最大的正方形(正方形木板有一边与三角形木板的底边重合).这块正方形木板的面积是________平方米.
?19.如图,在中,,,垂足为,,,则的长为________.
?20.一天,小青在校园内发现一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为米,由此可推断出树高是________米.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,与是位似图形,试说明与是否平行.
?
22.如图,中,,于,,,求.
?
23.在中,,,,将放在如图所示的平面直角坐标系中,且点、点在在轴上,是正半轴上一动点,把绕点逆时针旋转的度数,点旋转后的对应点为.
若时,则点的坐标是________.(直接写出结果)
若旋转后所得三角形和相似时,求此时点的坐标;
是否存在满足条件的点,使直线恰好过点;若存在,求出点的坐标,若不存在,请说明理由.
?
24.如图,和是等腰直角三角形,,点、在的外部,连结,.
求证:;
若将绕点旋转,直线交直线于点,交直线于点.
①如果,,求的值;
②当为等腰直角三角形时,请你直接写出的值.
?
25.已知:如图,在四边形中,,对角线、交于点,点在边上,连接交线段于点,.
求证:;
连接,求证:.
?
26.如图①,已知平面内一点与一直线,如果过点作直线,垂足为,那么垂足叫做点在直线上的射影;如果线段的两个端点和在直线上的射影分别为点和,那么线段叫做线段在直线上的射影.
如图①,已知平面内一点与一直线,如果过点作直线,垂足为,那么垂足叫做点在直线上的射影;如果线段的两个端点和在直线上的射影分别为点和,那么线段叫做线段在直线上的射影.
如图②,、为线段外两点,,,垂足分别为、.
则点在上的射影是________点,点在上的射影是________点,
线段在上的射影是________,线段在上的射影是________;
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
答案
1.A
2.B
3.B
4.C
5.D
6.D
7.C
8.D
9.C
10.A
11.
12.有两组角对应相等的两个三角形相似
13.
14.或
15.
16.
17.
18.
19.
20.
21.解:.
理由:∵与是位似图形,
∴,
∴,
∴.
22.解:如图,∵中,,,
∴.
又∵,,
∴,,
∴,
∴,即.
23.①如图中,当时满足条件,此时易知,,设,
在中,∵,
∴,
∴,
∴,,
由,可得,
∴,,
∴,
∴点坐标.
②如图中,若时,此时,点恰好与点重合,所以,
综上所述,点的坐标是.设点的坐标为,同法可得的坐标是,
设过,,则有,解得
∴,
把,代入,
化简得,解得,(不合题意,舍去),
∴点的坐标是.
24.解:∵
∴,
∴,
在和中,
,
∴,
∴;
①当点在线段上时(如图)
∵,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴.
∴,
当点在线段延长线上时(如图)
∵,
∴,
又∵,
∴,
∴,
∴;
∵,
∴,
∵,
∴
∴;
②如图,
当为等腰直角三角形时,
则,
.
25.证明:∵,
∴.
又∵,
∴.
∴.
∵,
∴.
∴.∵,,
∴.
∴.
又∵,
∴.
∴.
∴.
26.线段线段
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
