高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):20【提高】直线、平面垂直的性质
文档属性
| 名称 | 高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):20【提高】直线、平面垂直的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 671.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-02 00:00:00 | ||
图片预览




文档简介
直线、平面垂直的性质
【学习目标】
1.掌握直线与平面垂直的性质定理,并能解决有关问题;
2.掌握两个平面垂直的性质定理,并能解决有关问题;
3.能综合运用直线与平面、平面与平面的垂直、平行的判定和性质定理解决有关问题.
【要点梳理】
要点一、直线与平面垂直的性质
1.基本性质
文字语言:一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线.
符号语言:
图形语言:
2.性质定理
文字语言:垂直于同一个平面的两条直线平行.
符号语言:
图形语言:
3.直线与平面垂直的其他性质
(1)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。
(2)若于,,则。
(3)垂直于同一条直线的两个平面平行。
(4)如果一条直线垂直于两个平行平面中的一个,则它必垂直于另一个平面。
要点诠释:
线面垂直关系是线线垂直、面面垂直关系的枢纽,通过线面垂直可以实现线线垂直和面面垂直关系的相互转化。
要点二、平面与平面垂直的性质
1.性质定理
文字语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
符号语言:
图形语言:
要点诠释:
面面垂直的性质定理是作线面垂直的依据和方法,在解决二面角问题中作二面角的平面角经常用到。这种线面垂直与面面垂直间的相互转化,是我们立体几何中求解(证)问题的重要思想方法。
2.平面与平面垂直性质定理的推论
如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内。
要点三、垂直关系的综合转化
线线垂直、线面垂直、面面垂直是相互联系的,能够相互转化,转化的纽带是对应的定义、判定定理和性质定理,具体的转化关系如下图所示:
在解决问题时,可以从条件入手,分析已有的垂直关系,早从结论探求所需的关系,从而架起条件与结论的桥梁.
垂直间的关系可按下面的口诀记忆:
线面垂直的关键,定义来证最常见,
判定定理也常用,它的意义要记清.
平面之内两直线,两线交于一个点,
面外还有一条线,垂直两线是条件.
面面垂直要证好,原有图中去寻找,
若是这样还不好,辅助线面是个宝.
先作交线的垂线,面面转为线和面,
再证一步线和线,面面垂直即可见.
借助辅助线和面,加的时候不能乱,
以某性质为基础,不能主观凭臆断,
判断线和面垂直,线垂面中两交线.
两线垂直同一面,相互平行共伸展,
两面垂直同一线,一面平行另一面.
要让面和面垂直,面过另面一垂线,
面面垂直成直角,线面垂直记心间.
【典型例题】
类型一:直线与平面垂直的性质
例1.设a,b为异面直线,AB是它们的公垂线(与两异面直线都垂直且相交的直线)。
(1)若a,b都平行于平面,求证:AB⊥;
(2)若a,b分别垂直于平面,,且,求证:AB∥c。
【思路点拨】(1)依据直线和平面垂直的判定定理证明AB⊥,可先证明线与线的平行。(2)由于此时垂直的关系较多,因此可以考虑利用线面垂直的性质证明AB∥c。
证明:(1)如图(1),在内任取一点P,设直线a与点P确定的平面与平面的交线为a',设直线b与点P确定的平面与平面的交线为b'。
∵a∥,b∥,∴a∥a',b∥b'。
又∵AB⊥,AB⊥b,∴AB⊥a',AB⊥b',
∴AB⊥。
(2)如图,过B作BB'⊥,则AB⊥BB'。
又∵AB⊥b,∴AB垂直于由b和BB'确定的平面。
∵b⊥,∴b⊥c,∵BB'⊥,∴BB'⊥c。
∴c也垂直于由BB'和b确定的平面。
故c∥AB。
【总结升华】由第(2)问的证明可以看出,利用线面垂直的性质证明线与线的平行,其关键是构造平面,使所证线皆与该平面垂直。如题中,通过作出辅助线BB',构造出平面,即由相交直线b与BB'确定的平面,然后借助于题目中的其他垂直关系证明。
举一反三:
【变式1】 设,m是两条不同的直线,是一个平面,则下列命题正确的是( )
A.若⊥m,m,则⊥ B.若⊥,∥m,则m⊥
C.若∥,m,则∥m D.若∥,m∥,则∥m
【答案】B
【解析】两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。
例2.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)证明:AE⊥CD;
(2)证明:PD⊥平面ABE.
【思路点拨】(1)由PA⊥底面ABCD,可得 CD⊥PA,又CD⊥AC,故CD⊥面PAC,从而证得CD⊥AE;
(2)由等腰三角形的底边中线的性质可得AE⊥PC,由(Ⅰ)知CD⊥AE,从而AE⊥面PCD,AE⊥PD,再由 AB⊥PD 可得 PD⊥面ABE。
【解析】
(1)证明:在四棱锥P-ABCD中,PA⊥底面ABCD,CD?平面ABCD,∴CD⊥PA.
又CD⊥AC,PA∩AC=A,∴CD⊥面PAC,
∵AE?面PAC,故CD⊥AE.
(2)证明:由PA=AB=BC,∠ABC=60°,可得PA=AC,
∵E是PC的中点,∴AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,故AE⊥PD.
由(1)知,AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD.
而PD?平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,PD在底面ABCD内的射影是AD,AB⊥AD,∴AB⊥PD.
又∵AB∩AE=A,∴PD⊥面ABE
【总结升华】直线与平面垂直的性质定理(以及补充性质)是线线、线面垂直以及线面、面面平行相互转化的桥梁,因此必须熟练掌握这些定理,并能灵活地运用它们.
举一反三:
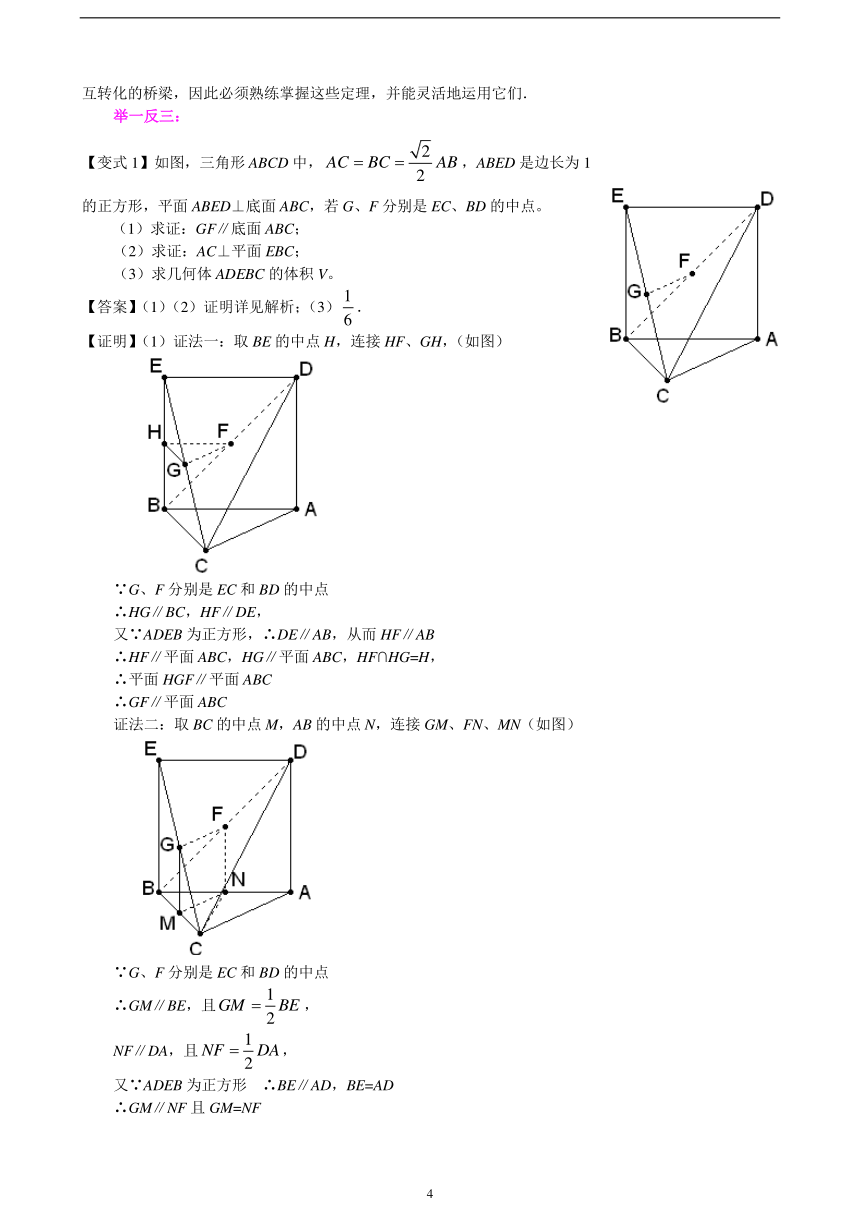
【变式1】如图,三角形ABCD中,,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点。
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V。
【答案】(1)(2)证明详见解析;(3).
【证明】(1)证法一:取BE的中点H,连接HF、GH,(如图)
∵G、F分别是EC和BD的中点
∴HG∥BC,HF∥DE,
又∵ADEB为正方形,∴DE∥AB,从而HF∥AB
∴HF∥平面ABC,HG∥平面ABC,HF∩HG=H,
∴平面HGF∥平面ABC
∴GF∥平面ABC
证法二:取BC的中点M,AB的中点N,连接GM、FN、MN(如图)
∵G、F分别是EC和BD的中点
∴GM∥BE,且,
NF∥DA,且,
又∵ADEB为正方形 ∴BE∥AD,BE=AD
∴GM∥NF且GM=NF
∴MNFG为平行四边形
∴GF∥MN,又MN平面ABC,
∴GF∥平面ABC
证法三:连接AE,
∵ADEB为正方形,
∴AE∩BD=F,且F是AE中点,
∴GF∥AC,
又AC平面ABC,
∴GF∥平面ABC
(2)∵ADEB为正方形,∴EB⊥AB,∴GF∥平面ABC
又∵平面ABED⊥平面ABC,∴BE⊥平面ABC
∴BE⊥AC
又∵CA2+CB2=AB2
∴AC⊥BC,
∵BC∩BE=B,
∴AC⊥平面BCE
(3)连接CN,因为AC=BC,∴CN⊥AB,
又平面ABED⊥平面ABC,CN平面ABC,∴CN⊥平面ABED。
∵三角形ABC是等腰直角三角形,∴,
∵C—ABED是四棱锥,
∴
类型二:平面与平面垂直的性质
例3.如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面。
【解析】已知:,,,求证:。
证法1:如图(左),在内取一点P,作PA垂直于与的交线于A,PB垂直于与的交线于B,则PA⊥,PB⊥,
∵,∴⊥PA,⊥PB。
∵PA,PB,PA∩PB=P,
∴。
证法2:如图(右),在内作直线m垂直于与的交线,在内作直线n垂直于与的交线,
∵,,∴,,∴m∥n。
又,∴m∥,∴m∥,∴。
证法3:如图,在上取一点A,过A作直线m,使。
∵,且,∴。
同理,∴,即与m重合。
∴。
【总结升华】证法1、证法2都是利用“两平面垂直时,在一个平面内垂直于两平面的交线的直线垂直于另一个平面”这一性质,添加了在一个平面内垂直于交线的直线这样的辅助线,这是证法1、证法2的关键。证法3利用两个平面垂直的推论,则较为简捷。由此可见,我们必须熟练掌握这一推论。
举一反三:
【变式1】已知△ABC,AB=AC=3a,BC=2a,D为BC的中点,在空间平移△ABC到△A1B1C1,连接对应顶点,且满足AA1平面ABC,AA1=3a。如图所示,E是CC1上一点,且CE=2a,求二面角D—AE—C的正弦值。
【解析】 ∵AA1⊥平面ABC,CC1∥AA1,∴CC1⊥平面ABC。
又CC1平面ACE,∴平面ACE⊥平面ABC。
作DH⊥AC于H,DH⊥平面AEC,作HF⊥AE于F,连接DF,
则DF⊥AE,∴∠DFH是二面角D—AE—C的平面角。
在Rt△ADC中,。
在Rt△ADE(易证得)中,。
在Rt△DHF中,。
∴二面角D—AE—C的正弦值为。
【总结升华】面面垂直的性质定理是作线面垂直的依据和方法(即若有两个平面垂直,则在一个平面内作垂直于交线的直线,则该直线必垂直于另一个平面),利用它可以作出二面角的平面的角、直线与平面所成的角、平面的垂线等。
类型三:综合应用
例4.(2017年 重庆模拟)如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,,点G为AC的中点。
(1)求证:EG∥平面ABF;
(2)求三棱锥B—AEG的体积;
(3)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由。
【思路点拨】(1)取AB中点M,连接MG,则EF∥MG,①即得证。
(2)转换三棱锥B—AEG为E—ABG即可求得体积。
(3)只要证明AE⊥CDE即可。
【答案】(1)略(2)(3)略
【证明】(1)证明:取AB中点M,连FM,GM。
∵G为对角线AC的中点,
∴GM∥AD,且,
又∵FE∥,
∴GM∥FE且GM=FE。
∴四边形GMFE为平行四边形,即EG∥FM。
又∵EG平面ABF,FM平面ABF,
∴EG∥平面ABF。
(2)作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E—ABG的高
∵ 在△AEF中,AF=FE,∠AFE=60°,
∴ △AEF是正三角形
∴ ∠AEF=60°,
由EF∥AD知∠EAD=60°,
∴
∴ 三棱锥BAEG的体积为
(3)平面BAE⊥平面DCE,证明如下:
∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴ CD⊥平面AFED,
∴ CD⊥AE
∵ 四边形AFED为梯形,FE∥AD,且∠AEF=60°,
∴ ∠FAD=120°
又在△AED中,EA=2,AD=4,∠EAD=60°,
由余弦定理,得
∴
∴ ED⊥AE
又∵ ED∩CD=D
∴ AE⊥平面DCE
又 AE面BAE
∴ 平面BAE⊥平面DCE
例5.如图1,在中,,分别为的中点,点为线段上的一点,将沿折起到的位置,使,如图2.
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)线段上是否存在点,使平面?说明理由.
【思路点拨】这是个折叠问题,要注意折叠前和折叠后线段的数量和位置关系的变化。
【解析】
(Ⅰ)因为D,E分别为AC,AB的中点,
所以DE∥BC,
又因为DE平面A1CB,
所以DE∥平面A1CB.
(Ⅱ)由已知得AC⊥BC且DE∥BC,
所以DE⊥AC.
所以DE⊥A1D.DE⊥CD.
所以DE⊥平面A1DC.
而A1F平面A1DC,
所以DE⊥A1F.
又因为A1F⊥CD,
所以A1F⊥平面BCDE.
所以A1F⊥BE.
(Ⅲ)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.
所以平面DEQ即为平面DEP.
由(Ⅱ)知,DE⊥平面A1DC,
所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.
所以A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.
举一反三:
【变式1】 如下图,已知三棱锥P—ABC中,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足。
(1)求证:PA⊥平面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形。
证明 : (1)如下图(左),在平面ABC内取一点D,作DF⊥AC于F。
因为平面PAC⊥平面ABC,且交线为AC,所以DF⊥平面PAC。
又PA平面PAC,所以DF⊥PA。
作DG⊥AB于G,同理可证DG⊥PA。
又因为DG、DF都在平面ABC内,且DG∩DF=D,
所以PA⊥平面ABC。
(2)连接BE并延长交PC于H,如上图(右)。
因为E是△PBC的垂心,所以PC⊥BE。
又已知AE是平面PBC的垂线,所以PC⊥AE。
所以PC⊥平面ABE,所以PC⊥AB。
又因为PA⊥平面ABC,所以PA⊥AB,
所以AB⊥平面PAC,所以AB⊥AC,
即△ABC是直角三角形。
【总结升华】 证明两个平面垂直,通常是通过证明线线垂直一线面垂直——面面垂直来实现的。因此,在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化,每一垂直的判定就是从某一垂直开始转向另一垂直,最终达到目的。
【变式2】(2018 哈尔滨模拟)如图,已知四棱锥P—ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)判定AE与PD是否垂直,并说明理由.
(2)设AB=2,若H为PD上的动点,若△AHE面积的最小值为,求四棱锥P—ABCD的体积.
【答案】(1)略;(2).
【证明】(1)AE⊥PD
因为四边形ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形.
因为E是BC的中点,
∴AE⊥BC,结合BC∥AD,得AE⊥AD
∵PA⊥平面ABCD,AE平面ABCD,
∴PA⊥AE
PA∩AD=A,且PA平面PAD,AD平面PAD
∴AE⊥平面PAD,又PD平面PAD
∴AE⊥PD
(2)由(1),EA⊥平面PAD,
∴EA⊥AH,即△AEH为直角三角形,
Rt⊥EAH中,,
当AH最短时,即AH⊥PD时,△AEH面积的最小
此时,.
又AD=2,所以∠ADH=45°,所以PA=2.
【总结升华】本题综合了直线与平面平行的判定、直线与平面垂直的性质和棱柱、棱锥、棱台的体积等几个知识点.在题中出现了探究性问题,请同学们留意在解题过程中“空间问题平面化的思路”,是立体几何常用的数学思想.
【变式3】如图,四棱锥中,,,侧面为等边三角形,.
(Ⅰ)证明:;
(Ⅱ)求与平面所成角的正弦值.
【答案】(1)略(2)
【解析】
(I)取AB中点E,连结DE、SE,
∴ 四边形BCDE为矩形,DE=CB=2,
∵ 侧面为等边三角形
∴
又∵SD=1,,
∴为直角.
又∵,
∴ AB⊥平面SDE,
∴.
又SD与两条相交直线AB、SE都垂直.
∴SD⊥平面SAB.
(II)作垂足为F,FG⊥BC,垂足为G,连结SG
∵ AB⊥平面SDE,
∴ 平面ABCD⊥平面SED.
∴ SF⊥平面ABCD,
∵
∴ ,
又 ∵FG⊥BC,
∴ BC⊥平面SFG,
∵
∴ 平面SBC⊥平面SFG.
作,H为垂足,则FH⊥平面SBC.
又∵在中, ,
在中,
∴ ,即F到平面SBC的距离为.
∵ ED//BC,
∴ ED//平面SBC,∴ E到平面SBC的距离d也是.
设AB与平面SBC所成的角为α,则.
【巩固练习】
1.下列说法中正确的是( )
①过平面外一点有且仅有一条直线和已知平面垂直;②过直线外一点有且仅有一个平面与已知直线垂直;③过平面外一点可作无数条直线与已知平面平行;④过直线外一点只能作一条直线与已知直线垂直.
A.①②③ B.①②③④ C.②③ D.②③④
2.设a、b是异面直线,下列命题中正确的是( )
A.过不在a、b上的一点P一定可作一条直线和a、b都相交
B.过不在a、b上的一点P一定可作一个平面和a、b都垂直
C.过a一定可作一个平面与b垂直
D.过a一定可作一个平面与b平行
3.已知平面、、,则下列命题中正确的是( )
A.,,则
B.,,则
C.,,,则a⊥b
D.,,a⊥b,则b⊥
4.给出下列四个命题:
①经过平面外一点有且仅有一个平面与已知平面垂直;②如果一条直线和两个垂直平面中的一个垂直,它必和另一个平行;③过不在平面内的一条直线可作无数个平面与已知平面垂直;④如果两个平面互相垂直,经过一个平面内一点与另一个平面垂直的直线在这个平面内.
其中正确的是( )
A.①③ B.②③ C.②③④ D.④
5.(2017年 安徽合肥一模)如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD
6.以等腰直角△ABC斜边BC上的高为棱,把它折成直二面角,则此时两条直角边的夹角为( )
A.30° B.45° C.60° D.90°
7.(2018 甘肃天水期末)如图,四边形ABCD中,AB=AD=CD=1,,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'—BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
A.A'C⊥BD
B.∠BA'C=90°
C.CA'与平面A'BD所成的角为30°
D.四面体A'—BCD的体积为
8.给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面与不垂直.
其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
9.平面平面,且,则和的位置关系是 .
10.在空间四边形中,、都是边长为1的正三角形,且平面平面.为空间各边上的中点,则四边形的面积是 .
11.(2017春 上海期中)如图所示,以等腰直角三角形ABC斜边BC上的高AD为折痕.使△ABD和△ACD折成互相垂直的两个平面,则∠BAC=________.
12.如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
13.(2018 陕西模拟)如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在边BC的何处,都有PE⊥AF.
14.如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由.
(3)如果PA=AB=2,求三棱锥B—CDF的体积.
【答案与解析】
1.【答案】A
【解析】 过直线a外一点P可作一平面与直线a垂直,平面内所有过P的直线均与垂直,从而④不正确.
2.【答案】D
【解析】 A不正确,若点P和直线a确定平面,当b∥时,满足条件的直线不存在;C不正确,只有a、b垂直时才能作出满足条件的平面.
3.【答案】B
【解析】 如图,A中,平面AA1B1B⊥平面A1B1C1D1,
平面AA1D1D⊥平面A1B1C1D1,而平面AA1B1B与平面A1D1D相交.
C中,平面AA1B1B∩平面AB1D1=D1B1,
平面AA1D1D∩平面AB1D1=AD1,
平面AA1B1B⊥平面AA1D1D,
而AB1与AD1不垂直;
D中,b不定在平面β内.
4.【答案】D
【解析】 过平面外一点可作一条直线与平面垂直,过该直线的任何一个平面都与已知平面垂直,①不对;若,,则或,②不对;③当平面外的直线是平面的垂线时可以作无数个,否则只能作一个,③不对.
5.【分析】设AC∩BD=O,由ABCD是正方形,得O是AC中点,从而OM∥PC,由此得到M是PA中点;设N为PB的中点,连结AN,则AN与PB不一定垂直,从而得到N不一定是PB中点;由已知得PA=AC,PD=DC,从而H为PC的中点;由AD∥BC,得到l∥AD∥BC.
【答案】B
【解析】设AC∩BD=O,∵ABCD是正方形,∴O是AC中点,
∵过BD且与PC平行的平面交PA于M点,∴OM∥PC,
∴M是PA中点,故A正确;
设N为PB的中点,连接AN,
∵PA与AB不一定相等,∴AN与PB不一定垂直,
∴过AC且与PB垂直的平面交PB于N点,则N不一定是PB的中点,故B错误;
∵四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,
∴PA=AC,PD=DC,
∴过AD且与PC垂直的平面交PC于H点,则H为PC的中点,故C正确;
∵AD∥BC,平面PAD与平面PCB有公共点P,
∴l∥AD∥BC,故D正确.
故选:B.
6.【答案】C
【解析】 如图,由题可知CD=BD=AD,∠BDC=90°,则 ,所以∠ABC=60°.
7.【答案】B
【解析】若A成立可得BD⊥A'D,产生矛盾,故A不正确;
由题设知:△BA'D为等腰Rt△,CD⊥平面A'BD,得BA'⊥平面A'CD,于是B正确;
由CA'与平面A'BD所成的角为∠CA'D=45°知C不正确;
,D不正确.
故选B.
8.【答案】D
【解析】 ①没有强调一个平面内的两条相交直线与另一个平面都平行,所以①错;②符合两个平面相互垂直的判定定理,所以②正确;③垂直于同一直线的两条直线可能平行,也可能相交或异面,所以③错;④根据两个平面垂直的性质定理易知④正确.故选D.
9.【答案】
【解析】设,,,,又,.
10.【答案】
【解析】画出空间四边形,由题意知,四边形是矩形,其中一边长是,一边长是,所以矩形的面积是.
11.【分析】设AB=AC=1,则,由已知条件推导出△ABC是正三角形,由此能求出结果.
【答案】60°
【解析】设AB=AC=1,则,
∵BD⊥平面ADC,CD平面ADC,
∴BD⊥CD,
∵△BDC是等腰直角三角形,
∴,
∴△ABC是正三角形,
∴∠BAC=60°.
故答案为:60°.
12.【答案】
【解析】如图,过D作DG⊥AF,垂足为G,连接GK,
∵平面ABD⊥平面ABC,又DK⊥AB,
∴DK⊥平面ABC,∴DK⊥AF.
∴AF⊥平面DKG,∴AF⊥GK.
容易得到,当F接近E点时,K接近AB的中点,当F接近C点时,K接近AB的四等分点.
所以t的取值范围是.
13.【解析】(1)当点E为BC的中点时,EF与平面PAC平行.
∵△PBC中,E、F分别为BC、PB的中点.
∴EF∥PC,又EF不包含于平面PAC,
而PC平面PAC,∴EF∥平面PAC
(2)证明:∵PA⊥平面ABCD,BE平面ABCD,
∴EB⊥PA,
又EB⊥AB,AB∩AP=A,AB,AP平面PAB,
∴EB⊥平面PAB,又AF平面PAB,
∴AF⊥BE,
又PA=PB=1,点F是PB的中点,
∴AF⊥PB,
又∵PB∩BE=B,PB,BEPBE,
∴AF⊥平面PBE.
∵PE平面PBE,∴AF⊥PE.
∴无论点E在边BC的何处,都有PE⊥AF.
14.【分析】(1)由已知条件,利用直线垂直于平面的判定定理,先推导出BD⊥平面APC,由此能够证明BD⊥FG.
(2)当G为EC中点时,FG∥平面PBD.根据题设条件,利用直线与平面平行的判定定理进行证明.
(3)三棱锥B—CDF的体积等于三棱锥F—BCD的体积,利用等积法能求出结果.
【答案】(1)略(2)略(3)
【证明】(1)证明:∵PA⊥面ABCD,四边形ABCD是正方形,
其对角线BD、AC交于点E,
∴PA⊥BD,AC⊥BD.
∴BD⊥平面APC,
∵FG平面PAC,∴BD⊥FG
(2)当G为EC中点,即时,FG∥平面PBD.
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG∥PE
而FG平面PBD,PB平面PBD,
故FG∥平面PBD.
(3)连结FE,FD,
∵F是PC中点,E是正方形ABCD对角线的交点,
∴FE∥PA,且,
∵PD⊥面ABCD,∴FE⊥面BCD,
∵,
∴三棱锥B—CDF的体积.
【学习目标】
1.掌握直线与平面垂直的性质定理,并能解决有关问题;
2.掌握两个平面垂直的性质定理,并能解决有关问题;
3.能综合运用直线与平面、平面与平面的垂直、平行的判定和性质定理解决有关问题.
【要点梳理】
要点一、直线与平面垂直的性质
1.基本性质
文字语言:一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线.
符号语言:
图形语言:
2.性质定理
文字语言:垂直于同一个平面的两条直线平行.
符号语言:
图形语言:
3.直线与平面垂直的其他性质
(1)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。
(2)若于,,则。
(3)垂直于同一条直线的两个平面平行。
(4)如果一条直线垂直于两个平行平面中的一个,则它必垂直于另一个平面。
要点诠释:
线面垂直关系是线线垂直、面面垂直关系的枢纽,通过线面垂直可以实现线线垂直和面面垂直关系的相互转化。
要点二、平面与平面垂直的性质
1.性质定理
文字语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
符号语言:
图形语言:
要点诠释:
面面垂直的性质定理是作线面垂直的依据和方法,在解决二面角问题中作二面角的平面角经常用到。这种线面垂直与面面垂直间的相互转化,是我们立体几何中求解(证)问题的重要思想方法。
2.平面与平面垂直性质定理的推论
如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内。
要点三、垂直关系的综合转化
线线垂直、线面垂直、面面垂直是相互联系的,能够相互转化,转化的纽带是对应的定义、判定定理和性质定理,具体的转化关系如下图所示:
在解决问题时,可以从条件入手,分析已有的垂直关系,早从结论探求所需的关系,从而架起条件与结论的桥梁.
垂直间的关系可按下面的口诀记忆:
线面垂直的关键,定义来证最常见,
判定定理也常用,它的意义要记清.
平面之内两直线,两线交于一个点,
面外还有一条线,垂直两线是条件.
面面垂直要证好,原有图中去寻找,
若是这样还不好,辅助线面是个宝.
先作交线的垂线,面面转为线和面,
再证一步线和线,面面垂直即可见.
借助辅助线和面,加的时候不能乱,
以某性质为基础,不能主观凭臆断,
判断线和面垂直,线垂面中两交线.
两线垂直同一面,相互平行共伸展,
两面垂直同一线,一面平行另一面.
要让面和面垂直,面过另面一垂线,
面面垂直成直角,线面垂直记心间.
【典型例题】
类型一:直线与平面垂直的性质
例1.设a,b为异面直线,AB是它们的公垂线(与两异面直线都垂直且相交的直线)。
(1)若a,b都平行于平面,求证:AB⊥;
(2)若a,b分别垂直于平面,,且,求证:AB∥c。
【思路点拨】(1)依据直线和平面垂直的判定定理证明AB⊥,可先证明线与线的平行。(2)由于此时垂直的关系较多,因此可以考虑利用线面垂直的性质证明AB∥c。
证明:(1)如图(1),在内任取一点P,设直线a与点P确定的平面与平面的交线为a',设直线b与点P确定的平面与平面的交线为b'。
∵a∥,b∥,∴a∥a',b∥b'。
又∵AB⊥,AB⊥b,∴AB⊥a',AB⊥b',
∴AB⊥。
(2)如图,过B作BB'⊥,则AB⊥BB'。
又∵AB⊥b,∴AB垂直于由b和BB'确定的平面。
∵b⊥,∴b⊥c,∵BB'⊥,∴BB'⊥c。
∴c也垂直于由BB'和b确定的平面。
故c∥AB。
【总结升华】由第(2)问的证明可以看出,利用线面垂直的性质证明线与线的平行,其关键是构造平面,使所证线皆与该平面垂直。如题中,通过作出辅助线BB',构造出平面,即由相交直线b与BB'确定的平面,然后借助于题目中的其他垂直关系证明。
举一反三:
【变式1】 设,m是两条不同的直线,是一个平面,则下列命题正确的是( )
A.若⊥m,m,则⊥ B.若⊥,∥m,则m⊥
C.若∥,m,则∥m D.若∥,m∥,则∥m
【答案】B
【解析】两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面。
例2.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)证明:AE⊥CD;
(2)证明:PD⊥平面ABE.
【思路点拨】(1)由PA⊥底面ABCD,可得 CD⊥PA,又CD⊥AC,故CD⊥面PAC,从而证得CD⊥AE;
(2)由等腰三角形的底边中线的性质可得AE⊥PC,由(Ⅰ)知CD⊥AE,从而AE⊥面PCD,AE⊥PD,再由 AB⊥PD 可得 PD⊥面ABE。
【解析】
(1)证明:在四棱锥P-ABCD中,PA⊥底面ABCD,CD?平面ABCD,∴CD⊥PA.
又CD⊥AC,PA∩AC=A,∴CD⊥面PAC,
∵AE?面PAC,故CD⊥AE.
(2)证明:由PA=AB=BC,∠ABC=60°,可得PA=AC,
∵E是PC的中点,∴AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,故AE⊥PD.
由(1)知,AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD.
而PD?平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,PD在底面ABCD内的射影是AD,AB⊥AD,∴AB⊥PD.
又∵AB∩AE=A,∴PD⊥面ABE
【总结升华】直线与平面垂直的性质定理(以及补充性质)是线线、线面垂直以及线面、面面平行相互转化的桥梁,因此必须熟练掌握这些定理,并能灵活地运用它们.
举一反三:
【变式1】如图,三角形ABCD中,,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点。
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V。
【答案】(1)(2)证明详见解析;(3).
【证明】(1)证法一:取BE的中点H,连接HF、GH,(如图)
∵G、F分别是EC和BD的中点
∴HG∥BC,HF∥DE,
又∵ADEB为正方形,∴DE∥AB,从而HF∥AB
∴HF∥平面ABC,HG∥平面ABC,HF∩HG=H,
∴平面HGF∥平面ABC
∴GF∥平面ABC
证法二:取BC的中点M,AB的中点N,连接GM、FN、MN(如图)
∵G、F分别是EC和BD的中点
∴GM∥BE,且,
NF∥DA,且,
又∵ADEB为正方形 ∴BE∥AD,BE=AD
∴GM∥NF且GM=NF
∴MNFG为平行四边形
∴GF∥MN,又MN平面ABC,
∴GF∥平面ABC
证法三:连接AE,
∵ADEB为正方形,
∴AE∩BD=F,且F是AE中点,
∴GF∥AC,
又AC平面ABC,
∴GF∥平面ABC
(2)∵ADEB为正方形,∴EB⊥AB,∴GF∥平面ABC
又∵平面ABED⊥平面ABC,∴BE⊥平面ABC
∴BE⊥AC
又∵CA2+CB2=AB2
∴AC⊥BC,
∵BC∩BE=B,
∴AC⊥平面BCE
(3)连接CN,因为AC=BC,∴CN⊥AB,
又平面ABED⊥平面ABC,CN平面ABC,∴CN⊥平面ABED。
∵三角形ABC是等腰直角三角形,∴,
∵C—ABED是四棱锥,
∴
类型二:平面与平面垂直的性质
例3.如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面。
【解析】已知:,,,求证:。
证法1:如图(左),在内取一点P,作PA垂直于与的交线于A,PB垂直于与的交线于B,则PA⊥,PB⊥,
∵,∴⊥PA,⊥PB。
∵PA,PB,PA∩PB=P,
∴。
证法2:如图(右),在内作直线m垂直于与的交线,在内作直线n垂直于与的交线,
∵,,∴,,∴m∥n。
又,∴m∥,∴m∥,∴。
证法3:如图,在上取一点A,过A作直线m,使。
∵,且,∴。
同理,∴,即与m重合。
∴。
【总结升华】证法1、证法2都是利用“两平面垂直时,在一个平面内垂直于两平面的交线的直线垂直于另一个平面”这一性质,添加了在一个平面内垂直于交线的直线这样的辅助线,这是证法1、证法2的关键。证法3利用两个平面垂直的推论,则较为简捷。由此可见,我们必须熟练掌握这一推论。
举一反三:
【变式1】已知△ABC,AB=AC=3a,BC=2a,D为BC的中点,在空间平移△ABC到△A1B1C1,连接对应顶点,且满足AA1平面ABC,AA1=3a。如图所示,E是CC1上一点,且CE=2a,求二面角D—AE—C的正弦值。
【解析】 ∵AA1⊥平面ABC,CC1∥AA1,∴CC1⊥平面ABC。
又CC1平面ACE,∴平面ACE⊥平面ABC。
作DH⊥AC于H,DH⊥平面AEC,作HF⊥AE于F,连接DF,
则DF⊥AE,∴∠DFH是二面角D—AE—C的平面角。
在Rt△ADC中,。
在Rt△ADE(易证得)中,。
在Rt△DHF中,。
∴二面角D—AE—C的正弦值为。
【总结升华】面面垂直的性质定理是作线面垂直的依据和方法(即若有两个平面垂直,则在一个平面内作垂直于交线的直线,则该直线必垂直于另一个平面),利用它可以作出二面角的平面的角、直线与平面所成的角、平面的垂线等。
类型三:综合应用
例4.(2017年 重庆模拟)如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,,点G为AC的中点。
(1)求证:EG∥平面ABF;
(2)求三棱锥B—AEG的体积;
(3)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由。
【思路点拨】(1)取AB中点M,连接MG,则EF∥MG,①即得证。
(2)转换三棱锥B—AEG为E—ABG即可求得体积。
(3)只要证明AE⊥CDE即可。
【答案】(1)略(2)(3)略
【证明】(1)证明:取AB中点M,连FM,GM。
∵G为对角线AC的中点,
∴GM∥AD,且,
又∵FE∥,
∴GM∥FE且GM=FE。
∴四边形GMFE为平行四边形,即EG∥FM。
又∵EG平面ABF,FM平面ABF,
∴EG∥平面ABF。
(2)作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E—ABG的高
∵ 在△AEF中,AF=FE,∠AFE=60°,
∴ △AEF是正三角形
∴ ∠AEF=60°,
由EF∥AD知∠EAD=60°,
∴
∴ 三棱锥BAEG的体积为
(3)平面BAE⊥平面DCE,证明如下:
∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴ CD⊥平面AFED,
∴ CD⊥AE
∵ 四边形AFED为梯形,FE∥AD,且∠AEF=60°,
∴ ∠FAD=120°
又在△AED中,EA=2,AD=4,∠EAD=60°,
由余弦定理,得
∴
∴ ED⊥AE
又∵ ED∩CD=D
∴ AE⊥平面DCE
又 AE面BAE
∴ 平面BAE⊥平面DCE
例5.如图1,在中,,分别为的中点,点为线段上的一点,将沿折起到的位置,使,如图2.
(Ⅰ)求证:平面;
(Ⅱ)求证:;
(Ⅲ)线段上是否存在点,使平面?说明理由.
【思路点拨】这是个折叠问题,要注意折叠前和折叠后线段的数量和位置关系的变化。
【解析】
(Ⅰ)因为D,E分别为AC,AB的中点,
所以DE∥BC,
又因为DE平面A1CB,
所以DE∥平面A1CB.
(Ⅱ)由已知得AC⊥BC且DE∥BC,
所以DE⊥AC.
所以DE⊥A1D.DE⊥CD.
所以DE⊥平面A1DC.
而A1F平面A1DC,
所以DE⊥A1F.
又因为A1F⊥CD,
所以A1F⊥平面BCDE.
所以A1F⊥BE.
(Ⅲ)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:
如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
又因为DE∥BC,所以DE∥PQ.
所以平面DEQ即为平面DEP.
由(Ⅱ)知,DE⊥平面A1DC,
所以DE⊥A1C.
又因为P是等腰三角形DA1C底边A1C的中点,
所以A1C⊥DP.
所以A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.
举一反三:
【变式1】 如下图,已知三棱锥P—ABC中,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足。
(1)求证:PA⊥平面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形。
证明 : (1)如下图(左),在平面ABC内取一点D,作DF⊥AC于F。
因为平面PAC⊥平面ABC,且交线为AC,所以DF⊥平面PAC。
又PA平面PAC,所以DF⊥PA。
作DG⊥AB于G,同理可证DG⊥PA。
又因为DG、DF都在平面ABC内,且DG∩DF=D,
所以PA⊥平面ABC。
(2)连接BE并延长交PC于H,如上图(右)。
因为E是△PBC的垂心,所以PC⊥BE。
又已知AE是平面PBC的垂线,所以PC⊥AE。
所以PC⊥平面ABE,所以PC⊥AB。
又因为PA⊥平面ABC,所以PA⊥AB,
所以AB⊥平面PAC,所以AB⊥AC,
即△ABC是直角三角形。
【总结升华】 证明两个平面垂直,通常是通过证明线线垂直一线面垂直——面面垂直来实现的。因此,在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化,每一垂直的判定就是从某一垂直开始转向另一垂直,最终达到目的。
【变式2】(2018 哈尔滨模拟)如图,已知四棱锥P—ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
(1)判定AE与PD是否垂直,并说明理由.
(2)设AB=2,若H为PD上的动点,若△AHE面积的最小值为,求四棱锥P—ABCD的体积.
【答案】(1)略;(2).
【证明】(1)AE⊥PD
因为四边形ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形.
因为E是BC的中点,
∴AE⊥BC,结合BC∥AD,得AE⊥AD
∵PA⊥平面ABCD,AE平面ABCD,
∴PA⊥AE
PA∩AD=A,且PA平面PAD,AD平面PAD
∴AE⊥平面PAD,又PD平面PAD
∴AE⊥PD
(2)由(1),EA⊥平面PAD,
∴EA⊥AH,即△AEH为直角三角形,
Rt⊥EAH中,,
当AH最短时,即AH⊥PD时,△AEH面积的最小
此时,.
又AD=2,所以∠ADH=45°,所以PA=2.
【总结升华】本题综合了直线与平面平行的判定、直线与平面垂直的性质和棱柱、棱锥、棱台的体积等几个知识点.在题中出现了探究性问题,请同学们留意在解题过程中“空间问题平面化的思路”,是立体几何常用的数学思想.
【变式3】如图,四棱锥中,,,侧面为等边三角形,.
(Ⅰ)证明:;
(Ⅱ)求与平面所成角的正弦值.
【答案】(1)略(2)
【解析】
(I)取AB中点E,连结DE、SE,
∴ 四边形BCDE为矩形,DE=CB=2,
∵ 侧面为等边三角形
∴
又∵SD=1,,
∴为直角.
又∵,
∴ AB⊥平面SDE,
∴.
又SD与两条相交直线AB、SE都垂直.
∴SD⊥平面SAB.
(II)作垂足为F,FG⊥BC,垂足为G,连结SG
∵ AB⊥平面SDE,
∴ 平面ABCD⊥平面SED.
∴ SF⊥平面ABCD,
∵
∴ ,
又 ∵FG⊥BC,
∴ BC⊥平面SFG,
∵
∴ 平面SBC⊥平面SFG.
作,H为垂足,则FH⊥平面SBC.
又∵在中, ,
在中,
∴ ,即F到平面SBC的距离为.
∵ ED//BC,
∴ ED//平面SBC,∴ E到平面SBC的距离d也是.
设AB与平面SBC所成的角为α,则.
【巩固练习】
1.下列说法中正确的是( )
①过平面外一点有且仅有一条直线和已知平面垂直;②过直线外一点有且仅有一个平面与已知直线垂直;③过平面外一点可作无数条直线与已知平面平行;④过直线外一点只能作一条直线与已知直线垂直.
A.①②③ B.①②③④ C.②③ D.②③④
2.设a、b是异面直线,下列命题中正确的是( )
A.过不在a、b上的一点P一定可作一条直线和a、b都相交
B.过不在a、b上的一点P一定可作一个平面和a、b都垂直
C.过a一定可作一个平面与b垂直
D.过a一定可作一个平面与b平行
3.已知平面、、,则下列命题中正确的是( )
A.,,则
B.,,则
C.,,,则a⊥b
D.,,a⊥b,则b⊥
4.给出下列四个命题:
①经过平面外一点有且仅有一个平面与已知平面垂直;②如果一条直线和两个垂直平面中的一个垂直,它必和另一个平行;③过不在平面内的一条直线可作无数个平面与已知平面垂直;④如果两个平面互相垂直,经过一个平面内一点与另一个平面垂直的直线在这个平面内.
其中正确的是( )
A.①③ B.②③ C.②③④ D.④
5.(2017年 安徽合肥一模)如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD
6.以等腰直角△ABC斜边BC上的高为棱,把它折成直二面角,则此时两条直角边的夹角为( )
A.30° B.45° C.60° D.90°
7.(2018 甘肃天水期末)如图,四边形ABCD中,AB=AD=CD=1,,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'—BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
A.A'C⊥BD
B.∠BA'C=90°
C.CA'与平面A'BD所成的角为30°
D.四面体A'—BCD的体积为
8.给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面与不垂直.
其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
9.平面平面,且,则和的位置关系是 .
10.在空间四边形中,、都是边长为1的正三角形,且平面平面.为空间各边上的中点,则四边形的面积是 .
11.(2017春 上海期中)如图所示,以等腰直角三角形ABC斜边BC上的高AD为折痕.使△ABD和△ACD折成互相垂直的两个平面,则∠BAC=________.
12.如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
13.(2018 陕西模拟)如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,点F是PB的中点,点E在边BC上移动.
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在边BC的何处,都有PE⊥AF.
14.如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由.
(3)如果PA=AB=2,求三棱锥B—CDF的体积.
【答案与解析】
1.【答案】A
【解析】 过直线a外一点P可作一平面与直线a垂直,平面内所有过P的直线均与垂直,从而④不正确.
2.【答案】D
【解析】 A不正确,若点P和直线a确定平面,当b∥时,满足条件的直线不存在;C不正确,只有a、b垂直时才能作出满足条件的平面.
3.【答案】B
【解析】 如图,A中,平面AA1B1B⊥平面A1B1C1D1,
平面AA1D1D⊥平面A1B1C1D1,而平面AA1B1B与平面A1D1D相交.
C中,平面AA1B1B∩平面AB1D1=D1B1,
平面AA1D1D∩平面AB1D1=AD1,
平面AA1B1B⊥平面AA1D1D,
而AB1与AD1不垂直;
D中,b不定在平面β内.
4.【答案】D
【解析】 过平面外一点可作一条直线与平面垂直,过该直线的任何一个平面都与已知平面垂直,①不对;若,,则或,②不对;③当平面外的直线是平面的垂线时可以作无数个,否则只能作一个,③不对.
5.【分析】设AC∩BD=O,由ABCD是正方形,得O是AC中点,从而OM∥PC,由此得到M是PA中点;设N为PB的中点,连结AN,则AN与PB不一定垂直,从而得到N不一定是PB中点;由已知得PA=AC,PD=DC,从而H为PC的中点;由AD∥BC,得到l∥AD∥BC.
【答案】B
【解析】设AC∩BD=O,∵ABCD是正方形,∴O是AC中点,
∵过BD且与PC平行的平面交PA于M点,∴OM∥PC,
∴M是PA中点,故A正确;
设N为PB的中点,连接AN,
∵PA与AB不一定相等,∴AN与PB不一定垂直,
∴过AC且与PB垂直的平面交PB于N点,则N不一定是PB的中点,故B错误;
∵四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,
∴PA=AC,PD=DC,
∴过AD且与PC垂直的平面交PC于H点,则H为PC的中点,故C正确;
∵AD∥BC,平面PAD与平面PCB有公共点P,
∴l∥AD∥BC,故D正确.
故选:B.
6.【答案】C
【解析】 如图,由题可知CD=BD=AD,∠BDC=90°,则 ,所以∠ABC=60°.
7.【答案】B
【解析】若A成立可得BD⊥A'D,产生矛盾,故A不正确;
由题设知:△BA'D为等腰Rt△,CD⊥平面A'BD,得BA'⊥平面A'CD,于是B正确;
由CA'与平面A'BD所成的角为∠CA'D=45°知C不正确;
,D不正确.
故选B.
8.【答案】D
【解析】 ①没有强调一个平面内的两条相交直线与另一个平面都平行,所以①错;②符合两个平面相互垂直的判定定理,所以②正确;③垂直于同一直线的两条直线可能平行,也可能相交或异面,所以③错;④根据两个平面垂直的性质定理易知④正确.故选D.
9.【答案】
【解析】设,,,,又,.
10.【答案】
【解析】画出空间四边形,由题意知,四边形是矩形,其中一边长是,一边长是,所以矩形的面积是.
11.【分析】设AB=AC=1,则,由已知条件推导出△ABC是正三角形,由此能求出结果.
【答案】60°
【解析】设AB=AC=1,则,
∵BD⊥平面ADC,CD平面ADC,
∴BD⊥CD,
∵△BDC是等腰直角三角形,
∴,
∴△ABC是正三角形,
∴∠BAC=60°.
故答案为:60°.
12.【答案】
【解析】如图,过D作DG⊥AF,垂足为G,连接GK,
∵平面ABD⊥平面ABC,又DK⊥AB,
∴DK⊥平面ABC,∴DK⊥AF.
∴AF⊥平面DKG,∴AF⊥GK.
容易得到,当F接近E点时,K接近AB的中点,当F接近C点时,K接近AB的四等分点.
所以t的取值范围是.
13.【解析】(1)当点E为BC的中点时,EF与平面PAC平行.
∵△PBC中,E、F分别为BC、PB的中点.
∴EF∥PC,又EF不包含于平面PAC,
而PC平面PAC,∴EF∥平面PAC
(2)证明:∵PA⊥平面ABCD,BE平面ABCD,
∴EB⊥PA,
又EB⊥AB,AB∩AP=A,AB,AP平面PAB,
∴EB⊥平面PAB,又AF平面PAB,
∴AF⊥BE,
又PA=PB=1,点F是PB的中点,
∴AF⊥PB,
又∵PB∩BE=B,PB,BEPBE,
∴AF⊥平面PBE.
∵PE平面PBE,∴AF⊥PE.
∴无论点E在边BC的何处,都有PE⊥AF.
14.【分析】(1)由已知条件,利用直线垂直于平面的判定定理,先推导出BD⊥平面APC,由此能够证明BD⊥FG.
(2)当G为EC中点时,FG∥平面PBD.根据题设条件,利用直线与平面平行的判定定理进行证明.
(3)三棱锥B—CDF的体积等于三棱锥F—BCD的体积,利用等积法能求出结果.
【答案】(1)略(2)略(3)
【证明】(1)证明:∵PA⊥面ABCD,四边形ABCD是正方形,
其对角线BD、AC交于点E,
∴PA⊥BD,AC⊥BD.
∴BD⊥平面APC,
∵FG平面PAC,∴BD⊥FG
(2)当G为EC中点,即时,FG∥平面PBD.
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG∥PE
而FG平面PBD,PB平面PBD,
故FG∥平面PBD.
(3)连结FE,FD,
∵F是PC中点,E是正方形ABCD对角线的交点,
∴FE∥PA,且,
∵PD⊥面ABCD,∴FE⊥面BCD,
∵,
∴三棱锥B—CDF的体积.
