沪科版九年级数学下册第24章圆单元检测试题(有答案)
文档属性
| 名称 | 沪科版九年级数学下册第24章圆单元检测试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 167.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-03 11:25:42 | ||
图片预览

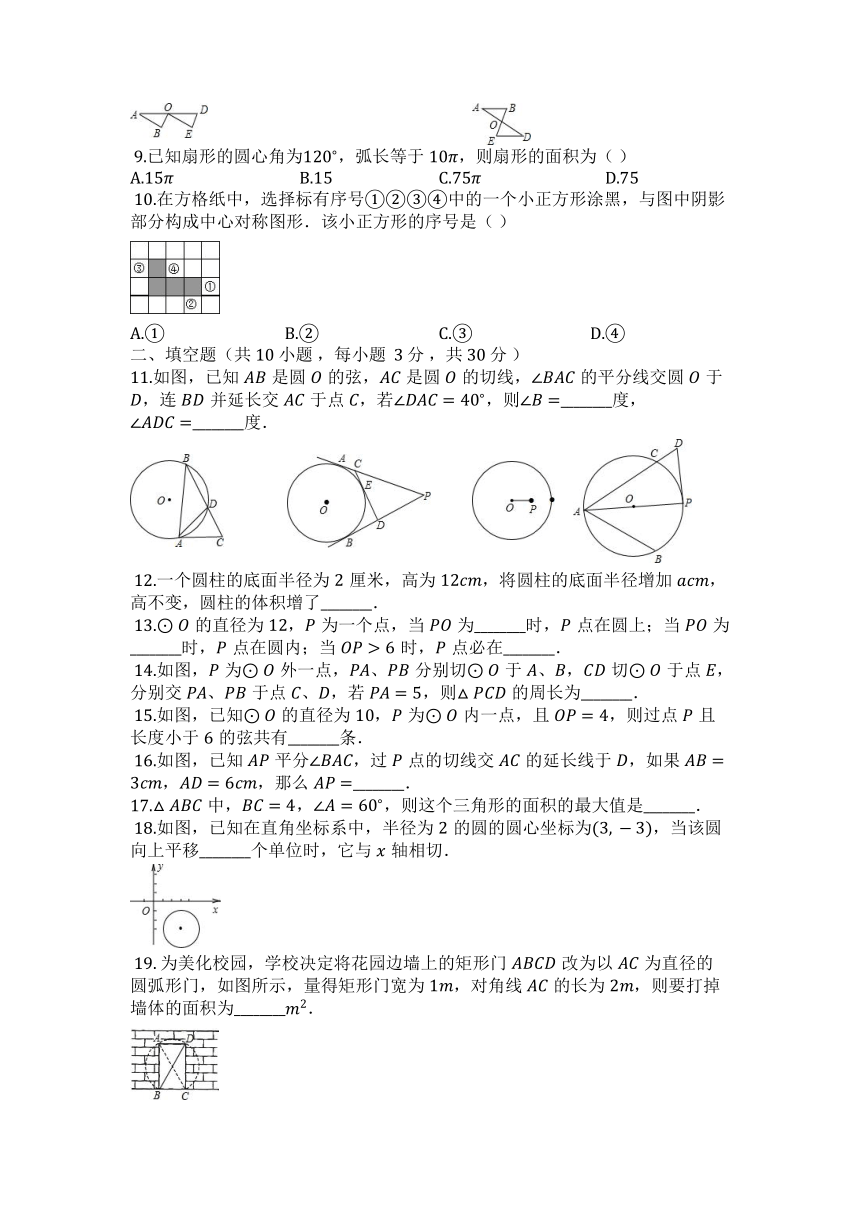
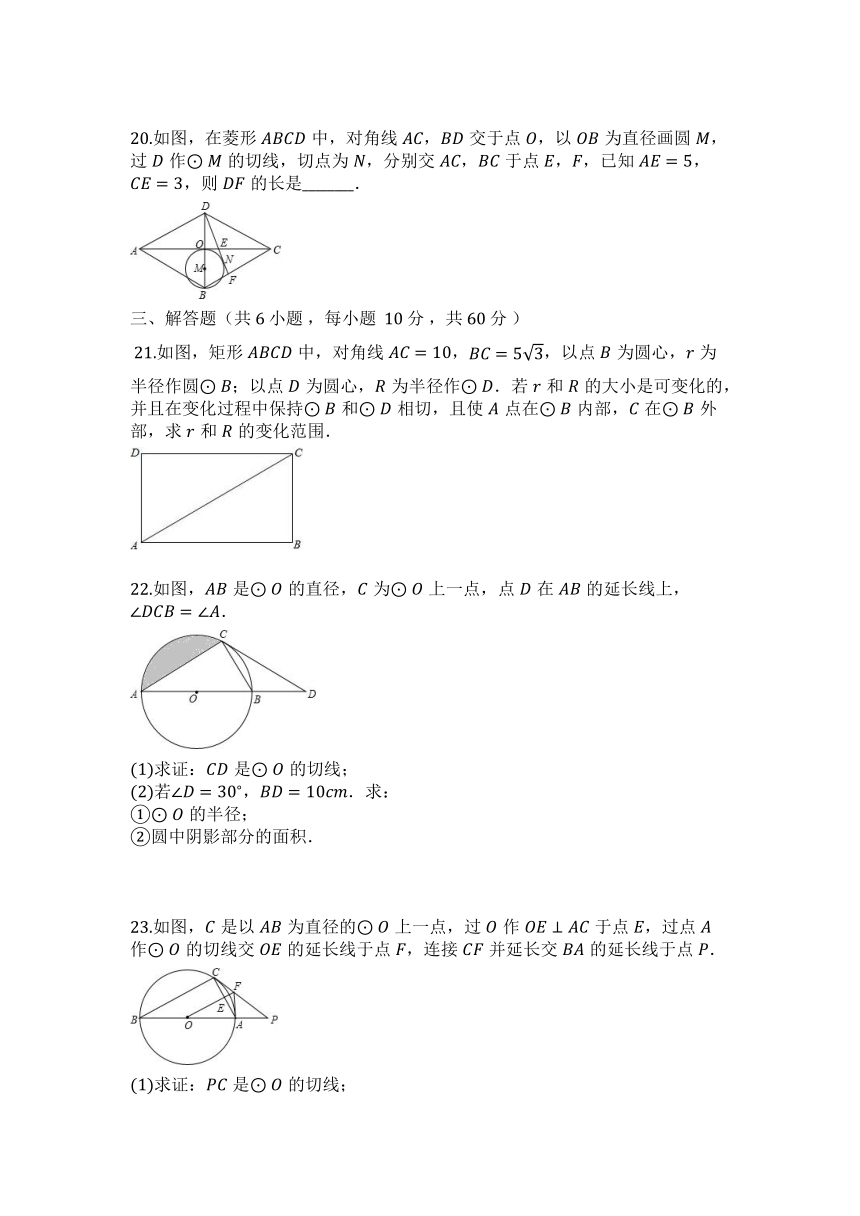

文档简介
沪科版九年级数学下册
第24章 圆 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,中,弦与直径相交于点,且,,,则的半径为( )
A. B. C. D.
?2.圆锥的底面半径为,母线长为,则该圆锥的侧面积为( )
A.л B.л C.л D.л
?3.在中,,,将这个三角形绕点旋转后,的中点落在点处,那么的长为( )
A. B. C. D.
?4.下列说法中,正确的是( )
A.到圆心的距离大于半径的点在圆内 B.圆的半径垂直于圆的切线
C.圆周角等于圆心角的一半 D.等弧所对的圆心角相等
?5.如果圆柱的轴截面是一个边长为的正方形,那么圆柱的侧面积为( )
A. B. C. D.
?6.若一个图形绕着一个定点旋转一个角后能够与原来的图形重合,那么这个图形叫做旋转对称图形.例如:等边三角形绕着它的中心旋转(如图),能够与原来的等边三角形重合,因而等边三角形是旋转对称图形.显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.下面四个图形中,旋转对称图形个数有( )
A. B. C. D.
?7.已知圆的半径为,如果一条直线上的个一点和圆心的距离为,那么这条直线和这个圆的位置关系是( )
A.相离 B.相交和相切
C.相交 D.都可能
?8.将绕点旋转得到,则下列作图正确的是( )
A. B.
C. D.
?9.已知扇形的圆心角为,弧长等于,则扇形的面积为( )
A. B. C. D.
?10.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.如图,已知是圆的弦,是圆的切线,的平分线交圆于,连并延长交于点,若,则________度,________度.
?12.一个圆柱的底面半径为厘米,高为,将圆柱的底面半径增加,高不变,圆柱的体积增了________.
?13.的直径为,为一个点,当为________时,点在圆上;当为________时,点在圆内;当时,点必在________.
?14.如图,为外一点,、分别切于、,切于点,分别交、于点、,若,则的周长为________.
?15.如图,已知的直径为,为内一点,且,则过点且长度小于的弦共有________条.
?16.如图,已知平分,过点的切线交的延长线于,如果,,那么________.
17.中,,,则这个三角形的面积的最大值是________.
?18.如图,已知在直角坐标系中,半径为的圆的圆心坐标为,当该圆向上平移________个单位时,它与轴相切.
?19.?为美化校园,学校决定将花园边墙上的矩形门改为以为直径的圆弧形门,如图所示,量得矩形门宽为,对角线的长为,则要打掉墙体的面积为________.
?
20.如图,在菱形中,对角线,交于点,以为直径画圆,过作的切线,切点为,分别交,于点,,已知,,则的长是________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,矩形中,对角线,,以点为圆心,为半径作圆;以点为圆心,为半径作.若和的大小是可变化的,并且在变化过程中保持和相切,且使点在内部,在外部,求和的变化范围.
?
22.如图,是的直径,为上一点,点在的延长线上,.
求证:是的切线;
若,.求:
①的半径;
②圆中阴影部分的面积.
?
23.如图,是以为直径的上一点,过作于点,过点作的切线交的延长线于点,连接并延长交的延长线于点.
求证:是的切线;
若,,求的长.
?24.如图所示,内接于,是的直径,点在上,过点的切线交的延长线于点,且,连接.
求证:;
若,,求的值.
?
25.如图,在中,半径垂直于弦,垂足为,点在的延长线上,若
求的度数;
若,求的长.
?
26.如图,四边形内接于圆,点在对角线上.
若,,求的度数;
若在上有一点,且,求证:.
答案
1.C
2.C
3.A
4.D
5.A
6.C
7.D
8.D
9.C
10.B
11.
12.
13.圆外
14.
15.
16.
17.
18.或
19.
20.
21.解:在中,∵,,
∴,
∵点在内部,在外部,
∴,
当和外切时,,则,
∴,
∴;
当和内切时,,则,
∴,
∴.
22.证明:连接,
∵是的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴是的切线;
解:①∵,
∴,,
∴是等边三角形,
∴,
∴;
②过作,
∵,,
∴,,
.
23.证明:连接,
∵为的直径,,又,
∴,
∴,,
∵,∴,
∴,
在和中,
,
∴,
∴,
∴是的切线;
设,则,
由切割线定理得,,
即,
解得,
∵,∴,
解得,.
24.证明:连接.
∵,
∴.
∵是的切线,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∴.
解:∵是的直径,
∴.
∴.
∵,,
∴.
∴.
∴,
∴,
∵,
∴,
∴.
25.解:
连接,
∵,,
∴,,
∵,,
∴,
∴,又,
∴;∵,
∴,
设的半径为,则,,
由勾股定理得,,
解得,
∵,,
∴.
26.解:∵,
∴,
∴,
∴,
∵四边形为圆内接四边形,
∴;∵,
∴,又,
∴,
∴,
∵,
∴,
∴,
∴.
第24章 圆 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,中,弦与直径相交于点,且,,,则的半径为( )
A. B. C. D.
?2.圆锥的底面半径为,母线长为,则该圆锥的侧面积为( )
A.л B.л C.л D.л
?3.在中,,,将这个三角形绕点旋转后,的中点落在点处,那么的长为( )
A. B. C. D.
?4.下列说法中,正确的是( )
A.到圆心的距离大于半径的点在圆内 B.圆的半径垂直于圆的切线
C.圆周角等于圆心角的一半 D.等弧所对的圆心角相等
?5.如果圆柱的轴截面是一个边长为的正方形,那么圆柱的侧面积为( )
A. B. C. D.
?6.若一个图形绕着一个定点旋转一个角后能够与原来的图形重合,那么这个图形叫做旋转对称图形.例如:等边三角形绕着它的中心旋转(如图),能够与原来的等边三角形重合,因而等边三角形是旋转对称图形.显然,中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.下面四个图形中,旋转对称图形个数有( )
A. B. C. D.
?7.已知圆的半径为,如果一条直线上的个一点和圆心的距离为,那么这条直线和这个圆的位置关系是( )
A.相离 B.相交和相切
C.相交 D.都可能
?8.将绕点旋转得到,则下列作图正确的是( )
A. B.
C. D.
?9.已知扇形的圆心角为,弧长等于,则扇形的面积为( )
A. B. C. D.
?10.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.如图,已知是圆的弦,是圆的切线,的平分线交圆于,连并延长交于点,若,则________度,________度.
?12.一个圆柱的底面半径为厘米,高为,将圆柱的底面半径增加,高不变,圆柱的体积增了________.
?13.的直径为,为一个点,当为________时,点在圆上;当为________时,点在圆内;当时,点必在________.
?14.如图,为外一点,、分别切于、,切于点,分别交、于点、,若,则的周长为________.
?15.如图,已知的直径为,为内一点,且,则过点且长度小于的弦共有________条.
?16.如图,已知平分,过点的切线交的延长线于,如果,,那么________.
17.中,,,则这个三角形的面积的最大值是________.
?18.如图,已知在直角坐标系中,半径为的圆的圆心坐标为,当该圆向上平移________个单位时,它与轴相切.
?19.?为美化校园,学校决定将花园边墙上的矩形门改为以为直径的圆弧形门,如图所示,量得矩形门宽为,对角线的长为,则要打掉墙体的面积为________.
?
20.如图,在菱形中,对角线,交于点,以为直径画圆,过作的切线,切点为,分别交,于点,,已知,,则的长是________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,矩形中,对角线,,以点为圆心,为半径作圆;以点为圆心,为半径作.若和的大小是可变化的,并且在变化过程中保持和相切,且使点在内部,在外部,求和的变化范围.
?
22.如图,是的直径,为上一点,点在的延长线上,.
求证:是的切线;
若,.求:
①的半径;
②圆中阴影部分的面积.
?
23.如图,是以为直径的上一点,过作于点,过点作的切线交的延长线于点,连接并延长交的延长线于点.
求证:是的切线;
若,,求的长.
?24.如图所示,内接于,是的直径,点在上,过点的切线交的延长线于点,且,连接.
求证:;
若,,求的值.
?
25.如图,在中,半径垂直于弦,垂足为,点在的延长线上,若
求的度数;
若,求的长.
?
26.如图,四边形内接于圆,点在对角线上.
若,,求的度数;
若在上有一点,且,求证:.
答案
1.C
2.C
3.A
4.D
5.A
6.C
7.D
8.D
9.C
10.B
11.
12.
13.圆外
14.
15.
16.
17.
18.或
19.
20.
21.解:在中,∵,,
∴,
∵点在内部,在外部,
∴,
当和外切时,,则,
∴,
∴;
当和内切时,,则,
∴,
∴.
22.证明:连接,
∵是的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴是的切线;
解:①∵,
∴,,
∴是等边三角形,
∴,
∴;
②过作,
∵,,
∴,,
.
23.证明:连接,
∵为的直径,,又,
∴,
∴,,
∵,∴,
∴,
在和中,
,
∴,
∴,
∴是的切线;
设,则,
由切割线定理得,,
即,
解得,
∵,∴,
解得,.
24.证明:连接.
∵,
∴.
∵是的切线,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∴.
解:∵是的直径,
∴.
∴.
∵,,
∴.
∴.
∴,
∴,
∵,
∴,
∴.
25.解:
连接,
∵,,
∴,,
∵,,
∴,
∴,又,
∴;∵,
∴,
设的半径为,则,,
由勾股定理得,,
解得,
∵,,
∴.
26.解:∵,
∴,
∴,
∴,
∵四边形为圆内接四边形,
∴;∵,
∴,又,
∴,
∴,
∵,
∴,
∴,
∴.
