华师大版九年级数学下册第26章二次函数单元检测试题(有答案)
文档属性
| 名称 | 华师大版九年级数学下册第26章二次函数单元检测试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 139.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-03 00:00:00 | ||
图片预览


文档简介
华师大版九年级数学下册_
第26章 _二次函数 _单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.若函数是二次函数且图象开口向上,则
A. B. C.或 D.或
?2.设,二次函数的图象为下列之一,则的值为( )
A. B.
C. D.
?3.把元的电器连续两次降价后的价格为元,若平均每次降价的百分率是,则与的函数关系式为( )
A. B.
C. D.
?4.抛物线的顶点坐标为( )
A. B.
C. D.
?5.已知二次函数的图象如图所示,给出以下结论:
①.②该函数的图象关于直线对称.③方程的两根是和.④时,随的增大而增大.其中正确结论的个数是( )
A. B. C. D.
?6.根据图象判断下列说法错误的是( )
A.函数的最大值等于 B.时,
C.当, D.当为或时,
?7.已知二次函数的图象如图所示,有下列个结论:
①;②;③;④;⑤(的实数);⑥
其中正确的结论有( )
A.个 B.个 C.个 D.个
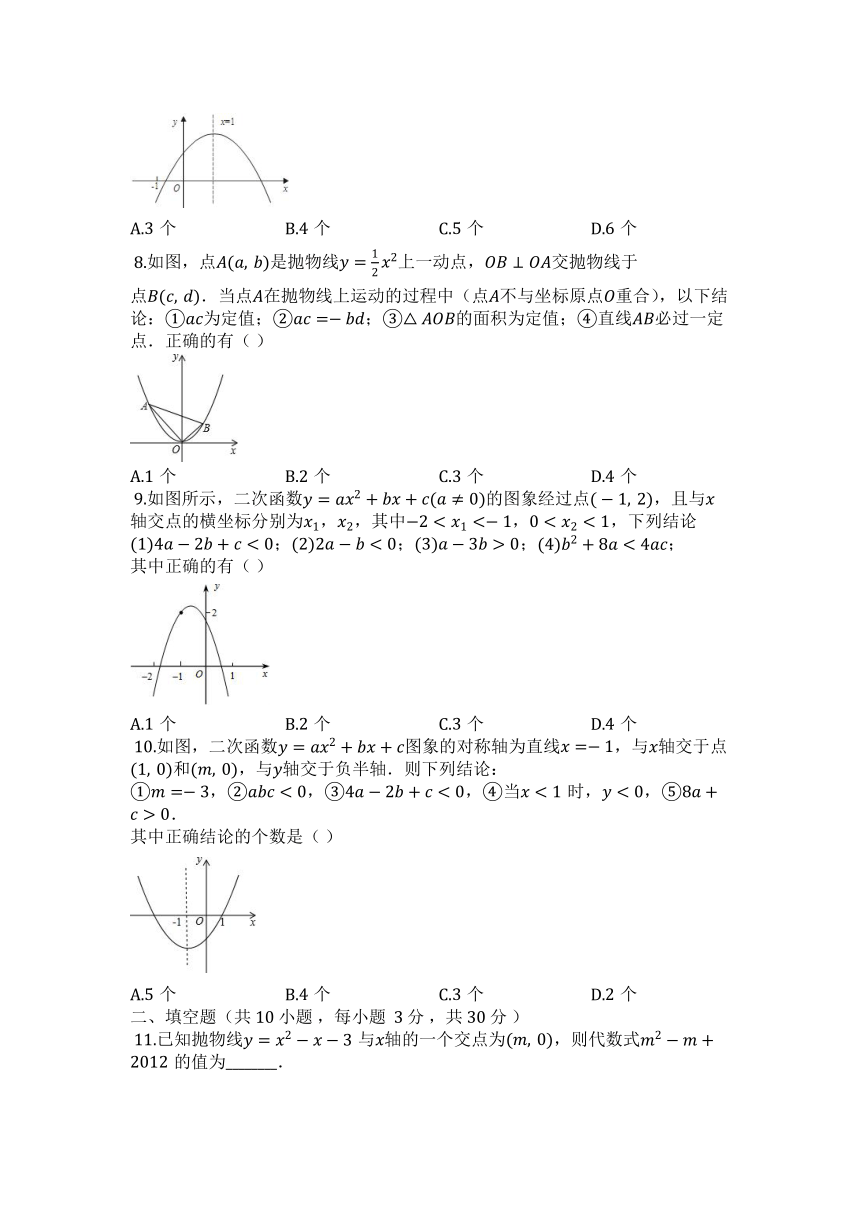
?8.如图,点是抛物线上一动点,交抛物线于点.当点在抛物线上运动的过程中(点不与坐标原点重合),以下结论:①为定值;②;③的面积为定值;④直线必过一定点.正确的有( )
A.个 B.个 C.个 D.个
?9.如图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,,其中,,下列结论
;;;;?
其中正确的有( )
A.个 B.个 C.个 D.个
?10.如图,二次函数图象的对称轴为直线,与轴交于点和,与轴交于负半轴.则下列结论:
①,②,③,④当时,,⑤.
其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知抛物线与轴的一个交点为,则代数式的值为________.
?
12.已知二次函数的图象经过点,,,那么这个二次函数的解析式为________.
?13.将抛物线向右平移个单位,再向下平移个单位后所得到的抛物线为________.
?14.二次函数,用配方法化为的形式为________.
?15.已知抛物线,当时有最小值.则这个最小值是________.
?16.已知二次函数的图象如图所示,以下关于,,的不等式中正确的序号是________.
①??②??③??④.
?17.已知二次函数的最小值为,则这个二次函数的解析式为________.
?18.如图是二次函数的图象,则________.
19.已知二次函数(、、是常数),图象如图所示,则当满足的条件是________时,.
?20.如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如图所示的坐标系,如果喷头所在处,水流路线最高处,如果不考虑其他因素,那么水池的半径至少要________,才能使喷出的水流不至落到池外.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.设二次函数的图象的对称轴是,在轴的截距的倒数和为,且经过点.
试求、、的值;
若或,求的取值范围;
当为何值时,有最大值?并求最大值.
?
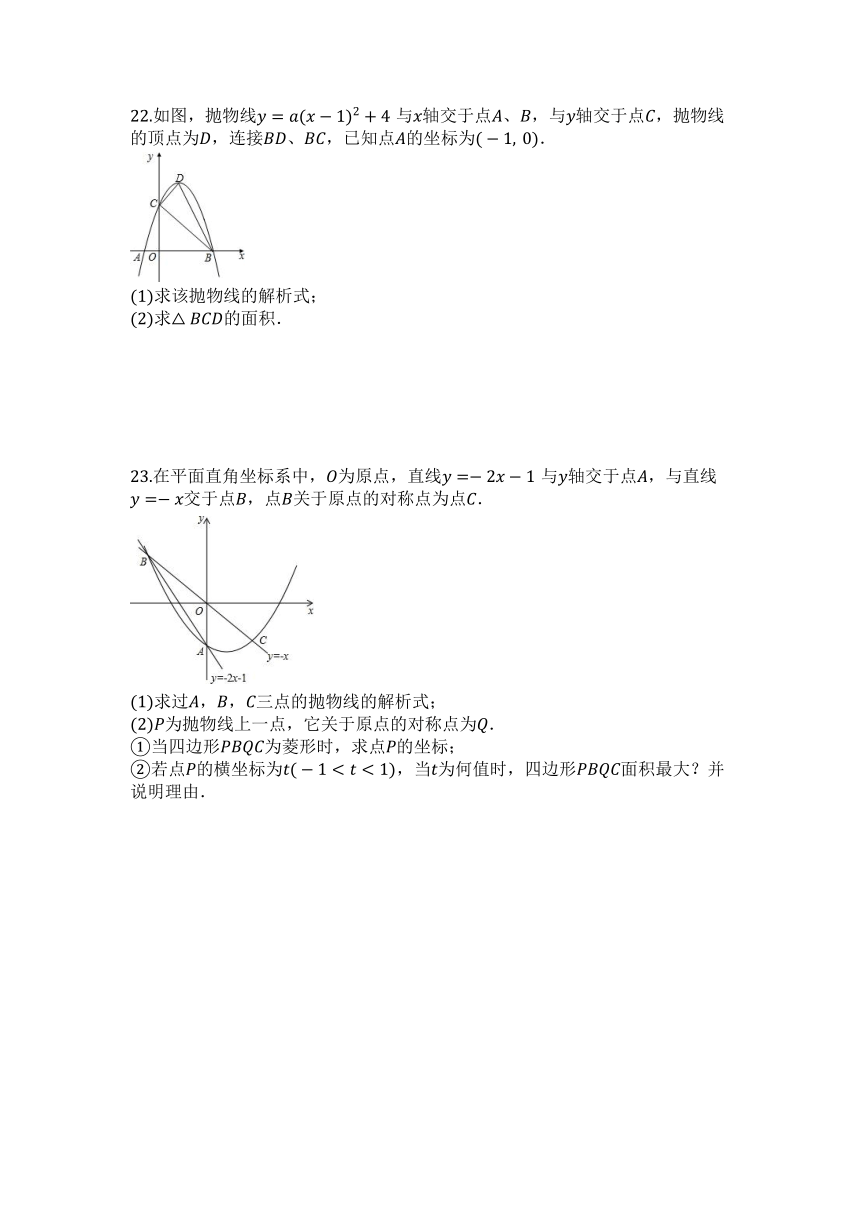
22.如图,抛物线与轴交于点、,与轴交于点,抛物线的顶点为,连接、,已知点的坐标为.
求该抛物线的解析式;
求的面积.
?
23.在平面直角坐标系中,为原点,直线与轴交于点,与直线交于点,点关于原点的对称点为点.
求过,,三点的抛物线的解析式;
为抛物线上一点,它关于原点的对称点为.
①当四边形为菱形时,求点的坐标;
②若点的横坐标为,当为何值时,四边形面积最大?并说明理由.
?
24.如图,抛物线经过点和点,与轴另外一个交点为.
求此二次函数的解析式;??????
若顶点为,则点坐标为:________;
求出两点之间的距离;????
当时,则的取值范围为:________.
?
25.如图,在中,,、的长恰好为方程的两根,且,为的中点.
求的值.
动点从点出发,沿的路线向点运动;点从点出发,沿的路线向点运动.若点、同时出发,速度都为每秒个单位,当点经过点时,点速度变为每秒单位,同时点速度变为每秒个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为秒.在整个运动过程中,设的面积为,试求与之间的函数关系式;并指出自变量的取值范围.
?
26.为了节能环保,新建的阜益路上路灯都是太阳能路灯.已知太阳能路灯售价为元/个,有甲、乙两经销商销售此产品.甲用如下方法促销:若购买路灯不超过个,按原价付款;若一次购买个以上,且购买的个数每增加一个,其价格减少元,但太阳能路灯的售价不得低于元/个.乙一律按原价的销售.现购买太阳能路灯个,如果全部在甲商家购买,则所需金额为元;如果全部在乙商家购买,则所需金额为元.
分别求出、与之间的函数关系式;
若政府投资万元,最多能购买多少个太阳能路灯?
答案
1.B
2.A
3.D
4.C
5.A
6.D
7.D
8.C
9.C
10.B
11.
12.
13.
14.
15.
16.①②③
17.
18.
19.
20.
21.解:设该抛物线与轴的交点横坐标是、.
则依题意得,即
解得.
则该抛物线的解析式为:;解:由知,该抛物线的解析式为:.
①当时,,即,
整理,得
,
解得
②当时,,
整理,得
,
解得或;
当即时,.
22.解:把点的坐标为代入,得
解得.
则该抛物线解析式为:;
如图,设直线与对称轴交于点.
∵抛物线的解析式为,
∴顶点坐标是,对称轴为,且.
又∵点的坐标为,
∴.
设直线的解析式为,则
,
解得.
则直线的解析式为:.
∴,
解得,
∴,
∴.
则的面积,即的面积是.
23.解:联立两直线解析式可得,解得,
∴点坐标为,
又点为点关于原点的对称点,
∴点坐标为,
∵直线与轴交于点,
∴点坐标为,
设抛物线解析式为,
把、、三点坐标代入可得,解得,
∴抛物线解析式为;①当四边形为菱形时,则,
∵直线解析式为,
∴直线解析式为,
联立抛物线解析式可得,解得或,
∴点坐标为或;
②当时,四边形的面积最大.
理由如下:
如图,过作,垂足为,作轴的垂线,交直线于点,
则,
∵线段长固定不变,
∴当最大时,四边形面积最大,
又(固定不变),
∴当最大时,也最大,
∵点在抛物线上,点在直线上,
∴点坐标为,点坐标为,
∴,
∴当时,有最大值,此时有最大值,即四边形的面积最大.
24.;在中,令,解得:或,则的坐标是,则;当时,则的取值范围为或.
故答案是:或.
25.解:∵、的长为方程的两根,
∴,
又∵,
∴,,
∴;作,垂足为,
∵,
∴.
又∵为的中点,
∴.
当时,由得,即,
解得,
,
当时,
同理,得.
26.解:由题意可知,
当时,购买一个需元,故;
当时,因为购买个数每增加一个,其价格减少元,但售价不得低于元/个,
所以.
即时,购买一个需元,故;
当时,购买一个需元,故;
所以;当时,;
当时,;
所以,由,解得;
由,解得.
故选择甲商家,最多能购买个路灯.
第26章 _二次函数 _单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.若函数是二次函数且图象开口向上,则
A. B. C.或 D.或
?2.设,二次函数的图象为下列之一,则的值为( )
A. B.
C. D.
?3.把元的电器连续两次降价后的价格为元,若平均每次降价的百分率是,则与的函数关系式为( )
A. B.
C. D.
?4.抛物线的顶点坐标为( )
A. B.
C. D.
?5.已知二次函数的图象如图所示,给出以下结论:
①.②该函数的图象关于直线对称.③方程的两根是和.④时,随的增大而增大.其中正确结论的个数是( )
A. B. C. D.
?6.根据图象判断下列说法错误的是( )
A.函数的最大值等于 B.时,
C.当, D.当为或时,
?7.已知二次函数的图象如图所示,有下列个结论:
①;②;③;④;⑤(的实数);⑥
其中正确的结论有( )
A.个 B.个 C.个 D.个
?8.如图,点是抛物线上一动点,交抛物线于点.当点在抛物线上运动的过程中(点不与坐标原点重合),以下结论:①为定值;②;③的面积为定值;④直线必过一定点.正确的有( )
A.个 B.个 C.个 D.个
?9.如图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,,其中,,下列结论
;;;;?
其中正确的有( )
A.个 B.个 C.个 D.个
?10.如图,二次函数图象的对称轴为直线,与轴交于点和,与轴交于负半轴.则下列结论:
①,②,③,④当时,,⑤.
其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知抛物线与轴的一个交点为,则代数式的值为________.
?
12.已知二次函数的图象经过点,,,那么这个二次函数的解析式为________.
?13.将抛物线向右平移个单位,再向下平移个单位后所得到的抛物线为________.
?14.二次函数,用配方法化为的形式为________.
?15.已知抛物线,当时有最小值.则这个最小值是________.
?16.已知二次函数的图象如图所示,以下关于,,的不等式中正确的序号是________.
①??②??③??④.
?17.已知二次函数的最小值为,则这个二次函数的解析式为________.
?18.如图是二次函数的图象,则________.
19.已知二次函数(、、是常数),图象如图所示,则当满足的条件是________时,.
?20.如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如图所示的坐标系,如果喷头所在处,水流路线最高处,如果不考虑其他因素,那么水池的半径至少要________,才能使喷出的水流不至落到池外.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.设二次函数的图象的对称轴是,在轴的截距的倒数和为,且经过点.
试求、、的值;
若或,求的取值范围;
当为何值时,有最大值?并求最大值.
?
22.如图,抛物线与轴交于点、,与轴交于点,抛物线的顶点为,连接、,已知点的坐标为.
求该抛物线的解析式;
求的面积.
?
23.在平面直角坐标系中,为原点,直线与轴交于点,与直线交于点,点关于原点的对称点为点.
求过,,三点的抛物线的解析式;
为抛物线上一点,它关于原点的对称点为.
①当四边形为菱形时,求点的坐标;
②若点的横坐标为,当为何值时,四边形面积最大?并说明理由.
?
24.如图,抛物线经过点和点,与轴另外一个交点为.
求此二次函数的解析式;??????
若顶点为,则点坐标为:________;
求出两点之间的距离;????
当时,则的取值范围为:________.
?
25.如图,在中,,、的长恰好为方程的两根,且,为的中点.
求的值.
动点从点出发,沿的路线向点运动;点从点出发,沿的路线向点运动.若点、同时出发,速度都为每秒个单位,当点经过点时,点速度变为每秒单位,同时点速度变为每秒个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为秒.在整个运动过程中,设的面积为,试求与之间的函数关系式;并指出自变量的取值范围.
?
26.为了节能环保,新建的阜益路上路灯都是太阳能路灯.已知太阳能路灯售价为元/个,有甲、乙两经销商销售此产品.甲用如下方法促销:若购买路灯不超过个,按原价付款;若一次购买个以上,且购买的个数每增加一个,其价格减少元,但太阳能路灯的售价不得低于元/个.乙一律按原价的销售.现购买太阳能路灯个,如果全部在甲商家购买,则所需金额为元;如果全部在乙商家购买,则所需金额为元.
分别求出、与之间的函数关系式;
若政府投资万元,最多能购买多少个太阳能路灯?
答案
1.B
2.A
3.D
4.C
5.A
6.D
7.D
8.C
9.C
10.B
11.
12.
13.
14.
15.
16.①②③
17.
18.
19.
20.
21.解:设该抛物线与轴的交点横坐标是、.
则依题意得,即
解得.
则该抛物线的解析式为:;解:由知,该抛物线的解析式为:.
①当时,,即,
整理,得
,
解得
②当时,,
整理,得
,
解得或;
当即时,.
22.解:把点的坐标为代入,得
解得.
则该抛物线解析式为:;
如图,设直线与对称轴交于点.
∵抛物线的解析式为,
∴顶点坐标是,对称轴为,且.
又∵点的坐标为,
∴.
设直线的解析式为,则
,
解得.
则直线的解析式为:.
∴,
解得,
∴,
∴.
则的面积,即的面积是.
23.解:联立两直线解析式可得,解得,
∴点坐标为,
又点为点关于原点的对称点,
∴点坐标为,
∵直线与轴交于点,
∴点坐标为,
设抛物线解析式为,
把、、三点坐标代入可得,解得,
∴抛物线解析式为;①当四边形为菱形时,则,
∵直线解析式为,
∴直线解析式为,
联立抛物线解析式可得,解得或,
∴点坐标为或;
②当时,四边形的面积最大.
理由如下:
如图,过作,垂足为,作轴的垂线,交直线于点,
则,
∵线段长固定不变,
∴当最大时,四边形面积最大,
又(固定不变),
∴当最大时,也最大,
∵点在抛物线上,点在直线上,
∴点坐标为,点坐标为,
∴,
∴当时,有最大值,此时有最大值,即四边形的面积最大.
24.;在中,令,解得:或,则的坐标是,则;当时,则的取值范围为或.
故答案是:或.
25.解:∵、的长为方程的两根,
∴,
又∵,
∴,,
∴;作,垂足为,
∵,
∴.
又∵为的中点,
∴.
当时,由得,即,
解得,
,
当时,
同理,得.
26.解:由题意可知,
当时,购买一个需元,故;
当时,因为购买个数每增加一个,其价格减少元,但售价不得低于元/个,
所以.
即时,购买一个需元,故;
当时,购买一个需元,故;
所以;当时,;
当时,;
所以,由,解得;
由,解得.
故选择甲商家,最多能购买个路灯.
