沪科版九年级数学上册第23章解直角三角形单元检测试题(有答案)
文档属性
| 名称 | 沪科版九年级数学上册第23章解直角三角形单元检测试题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-03 14:02:15 | ||
图片预览



文档简介
沪科版九年级数学上册
第23章 解直角三角形 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,太阳光线与地面成角,一棵倾斜的大树与地面成角,这时测得大树在地面的影长为,则大树的长为 .
A. B. C. D.
?2.在①,②,③,④这四个式子中,正确的是( )
A.①、③ B.②、④ C.①、④ D.③、④
?3.在中,,,,则的值是( )
A. B. C. D.
?4.如图是某商场一楼与二楼之间的手扶电梯示意图,其中、分别表示一楼、二楼地面的水平线,电梯坡面的坡度,则电梯坡面的坡角为( )
A. B. C. D.
?5.一斜坡长为,它的高为,将重物从斜坡下起点推到斜坡上处停下,停下地点的高度为( )
A. B. C. D.
?6.如图,已知正方形的边长为,如果将线段绕着点旋转后,点落在的延长线上的处,那么等于( )
A. B. C. D.
?7.如图,学校的保管室里,有一架米长的梯子斜靠在墙上,此时梯子与地面所成角为,如果梯子底端固定不动,顶端靠到对面墙上,此时梯子与地面所成的角为,则此保管室的宽度为( )
A.米 B.米
C.米 D.米
?8.汶川地震后,抢险队派一架直升飞机去、两个村庄抢险,飞机在距地面米上空的点,测得村的俯角为,村的俯角为(如图)则,两个村庄间的距离是( )米.
A. B. C. D.
?9.如图为了测量一条小河的宽度,可在点的左侧岸边选择一点使,若量得,,那么宽度为( )
A. B.
C. D.条件不足,无法计算
?10.某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头观测到水平雪道一端处的俯角为,另一端处的俯角为.若直升机镜头处的高度为米,点、、在同一直线上,则雪道的长度为( )
A.米 B.米
C.米 D.米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.如图河对岸有一古塔,小敏在处测得塔顶的仰角为,向塔前进米到达,在处测得的仰角为,则塔高为________米.
?12.如图,在一次测绘活动中,某同学站在点观测放置于,两处的标志物,数据显示点在点南偏东方向米处,点在点南偏西方向米处,则点与点的距离为________米.
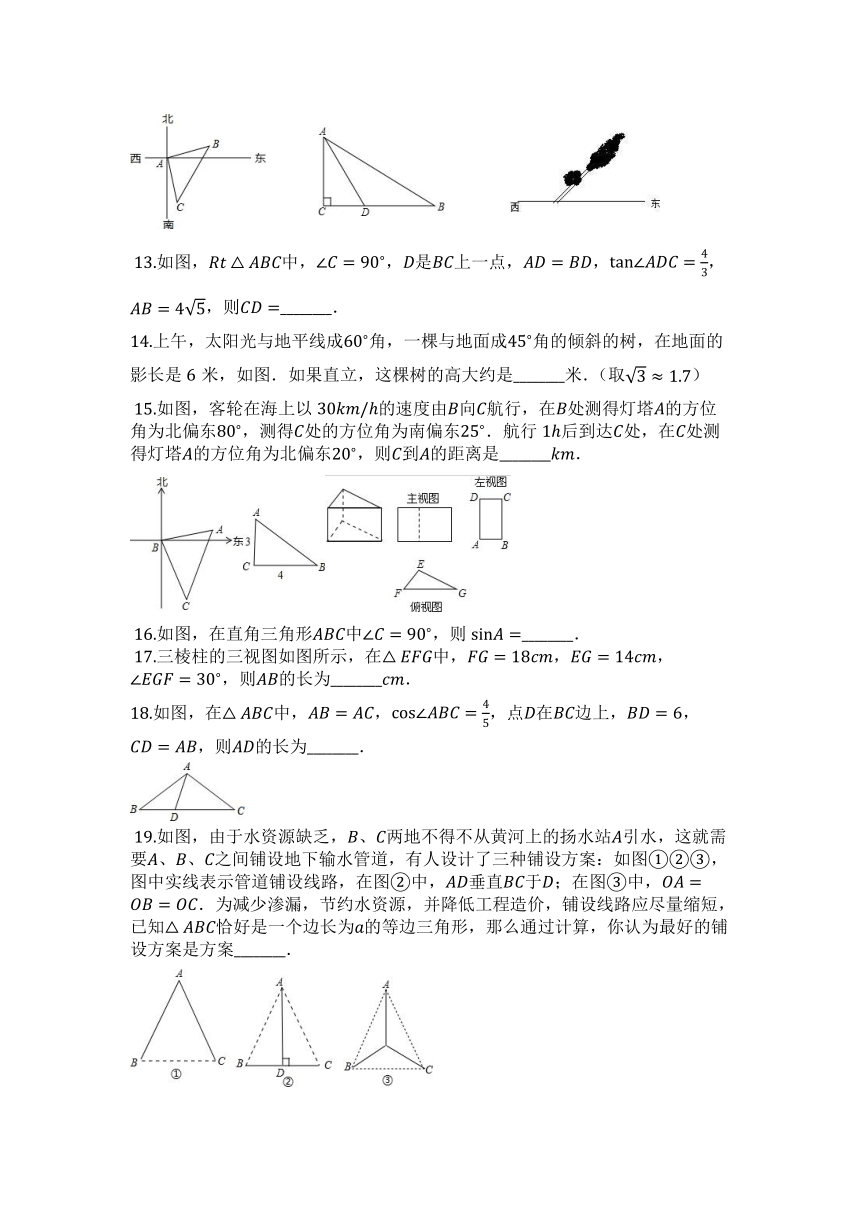
?13.如图,中,,是上一点,,,,则________.
14.上午,太阳光与地平线成角,一棵与地面成角的倾斜的树,在地面的影长是米,如图.如果直立,这棵树的高大约是________米.(取)
?15.如图,客轮在海上以的速度由向航行,在处测得灯塔的方位角为北偏东,测得处的方位角为南偏东.航行后到达处,在处测得灯塔的方位角为北偏东,则到的距离是________.
?16.如图,在直角三角形中,则________.
?17.三棱柱的三视图如图所示,在中,,,,则的长为________.
18.如图,在中,,,点在边上,,,则的长为________.
?19.如图,由于水资源缺乏,、两地不得不从黄河上的扬水站引水,这就需要、、之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,垂直于;在图③中,.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知恰好是一个边长为的等边三角形,那么通过计算,你认为最好的铺设方案是方案________.
?20.一艘轮船向正东航行,在处测得灯塔在的北偏东方向,航行小时到达处,此时测得灯塔在的北偏东方向上,且灯塔到轮船航线的距离是海里,则轮船的航行速度为________海里/小时.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.峨眉河是峨眉的一个风景点.如图,河的两岸平行于,河岸上有一排间隔为米的彩灯柱、、、…,小华在河岸的处测得,然后沿河岸走了米到达处,测得,求这条河的宽度(参考数据:,).
?
22.被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑.铁塔由塔身和塔座两部分组成.为了测得铁塔的高度,小莹利用自制的测角仪,在点测得塔顶的仰角为,在点测得塔顶的仰角为.已知测角仪的高为,的长为,所在的水平线于点.求铁塔的高(精确到).
?
23.如图,在大楼的正前方有一斜坡,米,坡角,小红在斜坡下的点处测得楼顶的仰角为,在斜坡上的点处测得楼顶的仰角为,其中点、、在同一直线上.
求斜坡的高度;
求大楼的高度(结果保留根号)
?24.补给船在点处接到命令,要求它向正在航行的军舰运送物资.已知军舰在补给船的西北方向海里的点处,正以每小时海里的速度向南偏东度的方向航行.如果补给船立即沿正西方向航行,恰好能在点处与军舰相遇,求补给船行驶的路程和时间.(结果保留根号)
?
25.如图所示,某小区一栋新建住宅楼正前方有一栋高度是米的旧楼房,从新楼顶端处测得在其正前方的旧楼的顶端的仰角是,旧楼底端到新楼前梯坎底边的距离是米,梯坎坡长是米,梯坎坡度,春节期间居委会想在之间悬挂一条彩带来烘托节日气氛,求这条彩带的长度和新建住宅楼的高度.
?
26.如图,已知点周围米范围内为原始森林保护区,在点测得点在
北偏东方向上,从点向东走米到达点,在点测得在北偏西方向上.
求点到直线的距离(结果保留根号);
如果以为中轴线修一条宽为米公路,那么公路会穿过原始森林保护区吗?说明理由.
答案
1.B
2.B
3.D
4.B
5.A
6.B
7.A
8.D
9.C
10.D
11.
12.
13.
14.
15.
16.
17.
18.
19.③
20.
21.峨眉河的宽度约为米.
22.铁塔的高为.
23.解:在中,米,,,
∴米;
过作,交于点,
∵,,
∴,即为等腰直角三角形,
设米,
∵四边形为矩形,
∴米,即米,
在中,,
∴米,
米,米,
∵,,
∴,
在中,根据勾股定理得:,
解得:或,
则米或米.
24.补给船行驶的路程为:海里,行驶的时为:小时.
25.解:作于点,于点,如右图所示,
由题意可得,
,米,米,梯坎坡长是米,梯坎坡度,
∴米,米,
∴米,
∴米,米,
∴米,
即这条彩带的长度是米,新建住宅楼的高度是米.
26.解:过点作于,
由已知得:,,,,米,
∴,,
设米,
在中,,
∴米,
在中,(米),
∴,
解得:;
∴点到直线的距离为:米;
公路不会穿过原始森林保护区.
理由:∵(米),
又∵以为中轴线修一条宽为米公路,
∴点到公路距离为:(米),
∵,
∴公路不会穿过原始森林保护区.
第23章 解直角三角形 单元检测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,太阳光线与地面成角,一棵倾斜的大树与地面成角,这时测得大树在地面的影长为,则大树的长为 .
A. B. C. D.
?2.在①,②,③,④这四个式子中,正确的是( )
A.①、③ B.②、④ C.①、④ D.③、④
?3.在中,,,,则的值是( )
A. B. C. D.
?4.如图是某商场一楼与二楼之间的手扶电梯示意图,其中、分别表示一楼、二楼地面的水平线,电梯坡面的坡度,则电梯坡面的坡角为( )
A. B. C. D.
?5.一斜坡长为,它的高为,将重物从斜坡下起点推到斜坡上处停下,停下地点的高度为( )
A. B. C. D.
?6.如图,已知正方形的边长为,如果将线段绕着点旋转后,点落在的延长线上的处,那么等于( )
A. B. C. D.
?7.如图,学校的保管室里,有一架米长的梯子斜靠在墙上,此时梯子与地面所成角为,如果梯子底端固定不动,顶端靠到对面墙上,此时梯子与地面所成的角为,则此保管室的宽度为( )
A.米 B.米
C.米 D.米
?8.汶川地震后,抢险队派一架直升飞机去、两个村庄抢险,飞机在距地面米上空的点,测得村的俯角为,村的俯角为(如图)则,两个村庄间的距离是( )米.
A. B. C. D.
?9.如图为了测量一条小河的宽度,可在点的左侧岸边选择一点使,若量得,,那么宽度为( )
A. B.
C. D.条件不足,无法计算
?10.某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头观测到水平雪道一端处的俯角为,另一端处的俯角为.若直升机镜头处的高度为米,点、、在同一直线上,则雪道的长度为( )
A.米 B.米
C.米 D.米
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.如图河对岸有一古塔,小敏在处测得塔顶的仰角为,向塔前进米到达,在处测得的仰角为,则塔高为________米.
?12.如图,在一次测绘活动中,某同学站在点观测放置于,两处的标志物,数据显示点在点南偏东方向米处,点在点南偏西方向米处,则点与点的距离为________米.
?13.如图,中,,是上一点,,,,则________.
14.上午,太阳光与地平线成角,一棵与地面成角的倾斜的树,在地面的影长是米,如图.如果直立,这棵树的高大约是________米.(取)
?15.如图,客轮在海上以的速度由向航行,在处测得灯塔的方位角为北偏东,测得处的方位角为南偏东.航行后到达处,在处测得灯塔的方位角为北偏东,则到的距离是________.
?16.如图,在直角三角形中,则________.
?17.三棱柱的三视图如图所示,在中,,,,则的长为________.
18.如图,在中,,,点在边上,,,则的长为________.
?19.如图,由于水资源缺乏,、两地不得不从黄河上的扬水站引水,这就需要、、之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,垂直于;在图③中,.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知恰好是一个边长为的等边三角形,那么通过计算,你认为最好的铺设方案是方案________.
?20.一艘轮船向正东航行,在处测得灯塔在的北偏东方向,航行小时到达处,此时测得灯塔在的北偏东方向上,且灯塔到轮船航线的距离是海里,则轮船的航行速度为________海里/小时.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.峨眉河是峨眉的一个风景点.如图,河的两岸平行于,河岸上有一排间隔为米的彩灯柱、、、…,小华在河岸的处测得,然后沿河岸走了米到达处,测得,求这条河的宽度(参考数据:,).
?
22.被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑.铁塔由塔身和塔座两部分组成.为了测得铁塔的高度,小莹利用自制的测角仪,在点测得塔顶的仰角为,在点测得塔顶的仰角为.已知测角仪的高为,的长为,所在的水平线于点.求铁塔的高(精确到).
?
23.如图,在大楼的正前方有一斜坡,米,坡角,小红在斜坡下的点处测得楼顶的仰角为,在斜坡上的点处测得楼顶的仰角为,其中点、、在同一直线上.
求斜坡的高度;
求大楼的高度(结果保留根号)
?24.补给船在点处接到命令,要求它向正在航行的军舰运送物资.已知军舰在补给船的西北方向海里的点处,正以每小时海里的速度向南偏东度的方向航行.如果补给船立即沿正西方向航行,恰好能在点处与军舰相遇,求补给船行驶的路程和时间.(结果保留根号)
?
25.如图所示,某小区一栋新建住宅楼正前方有一栋高度是米的旧楼房,从新楼顶端处测得在其正前方的旧楼的顶端的仰角是,旧楼底端到新楼前梯坎底边的距离是米,梯坎坡长是米,梯坎坡度,春节期间居委会想在之间悬挂一条彩带来烘托节日气氛,求这条彩带的长度和新建住宅楼的高度.
?
26.如图,已知点周围米范围内为原始森林保护区,在点测得点在
北偏东方向上,从点向东走米到达点,在点测得在北偏西方向上.
求点到直线的距离(结果保留根号);
如果以为中轴线修一条宽为米公路,那么公路会穿过原始森林保护区吗?说明理由.
答案
1.B
2.B
3.D
4.B
5.A
6.B
7.A
8.D
9.C
10.D
11.
12.
13.
14.
15.
16.
17.
18.
19.③
20.
21.峨眉河的宽度约为米.
22.铁塔的高为.
23.解:在中,米,,,
∴米;
过作,交于点,
∵,,
∴,即为等腰直角三角形,
设米,
∵四边形为矩形,
∴米,即米,
在中,,
∴米,
米,米,
∵,,
∴,
在中,根据勾股定理得:,
解得:或,
则米或米.
24.补给船行驶的路程为:海里,行驶的时为:小时.
25.解:作于点,于点,如右图所示,
由题意可得,
,米,米,梯坎坡长是米,梯坎坡度,
∴米,米,
∴米,
∴米,米,
∴米,
即这条彩带的长度是米,新建住宅楼的高度是米.
26.解:过点作于,
由已知得:,,,,米,
∴,,
设米,
在中,,
∴米,
在中,(米),
∴,
解得:;
∴点到直线的距离为:米;
公路不会穿过原始森林保护区.
理由:∵(米),
又∵以为中轴线修一条宽为米公路,
∴点到公路距离为:(米),
∵,
∴公路不会穿过原始森林保护区.
