2019年6月浙江省普通高中学业水平考试数学试卷
文档属性
| 名称 | 2019年6月浙江省普通高中学业水平考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 950.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-03 19:45:58 | ||
图片预览


文档简介
2019年6月浙江省普通高中学业水平考试数学试卷
若x>0,f(x)=-+a+|x-1
当0即--x+a+1≥(a-1)x+2
所以,a≥-1
∈R
当1即+x+a-1≥(a-1)x+2,
(x=1(2x=12≥a(x-1),
得
所以,a≤
综上所述,0≤a≤1
、选择题(本大题共18小题,每小题3分,共54分。每小题列出的四个选项中只有一个是符
合题目要求的,不选、多选、错选均不得分。)
1.已知集合A=(1,2,3},B={3,4,5,6},则A∩B=
A.{3}
B.{1,2
C.{4,5,6}
D.{1,2,3,4,5,6
2.函数f(x)=loga(4-x)(a>0,且a≠1)的定义域是
A.(0,4)
B.(4,+
D.(-∞,4)U(4,+∞)
3.圆(x-3)2+(y+2)2=16的圆心坐标是
A.(-3,2)
C.(-2,3
4.一元二次不等式x(9-x)>0的解集是
A.{x|x<0或x>9}
B.{x|0C.{xx<-9或x>0}
D.{x|-95椭圆x+y=1的焦点坐标是
A.(0,3),(0,-3)
B.(3,0),(—3,0)
C.(0,√41),(0,-√41)
D.(√41,0),(-√41,0)
6.已知空间向量a=(-1,1,3),b=(2,-2,x),若a∥b,则实数x的值是
4
4
7. cos2
T一S18
A
B
√2
8若实数x,y满足不等式组{x+y≤1,则2x+y的最小值是
A.3
B.
C.0
9.平面a与平面β平行的条件可以是
A.a内有无穷多条直线都与β平行
B.直线a∥a,a∥B,且直线a不在a内,也不在β内
C.直线aCa,直线bCB,且a∥B,b∥a
D.a内的任何直线都与B平行
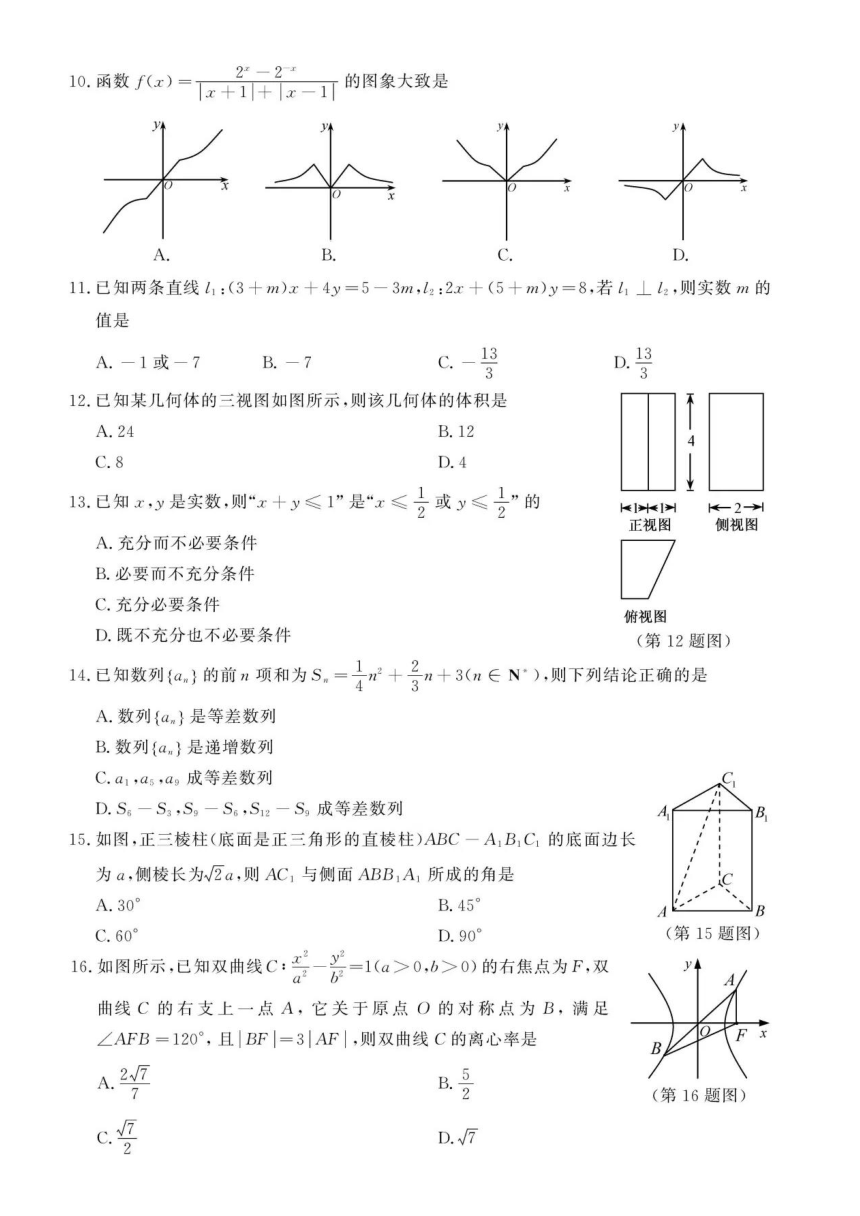
10,函数f(z)=1x+1+1x-1千的图象大致是
B
D
11.已知两条直线l1:(3+m)x+4y=5-3m,l2:2x+(5+m)y=8,若l1⊥l2,则实数m的
值是
A.-1或-7
B.—7
C.
12.已知某几何体的三视图如图所示,则该几何体的体积是
A.24
B.12
C.8
D.4
13.已知x,y是实数,则“x+y≤1”是“x≤1或y≤1”的
k∈lx∈l
正视图
侧视图
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
俯视图
D.既不充分也不必要条件
(第12题图)
14.已知数列{an}的前n项和为Sn=n2+2n+3(n∈N),则下列结论正确的是
A.数列{an}是等差数列
B.数列{an}是递增数列
C.a1,a5,a成等差数列
D.S6-S3,S-S6,S12-S成等差数列
B
15.如图,正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1的底面边长
为a,侧棱长为2a,则AC1与侧面ABB1A1所成的角是
A.30
B.45°
B
C.60
D.90
(第15题图)
16.如图所示,已知双曲线C:之2y2=1(a>0,b>0)的右焦点为F,双
b2
曲线C的右支上一点A,它关于原点O的对称点为B,满足
∠AFB=120°,且BF|=3AF|,则双曲线C的离心率是
F
B
(第16题图)
D
an+1,n为奇数,
17.已知数列{an}满足an为偶数,
(n∈N),若2≤a10≤3,则a1的取值范围
是
A.1≤a1≤10
B.1≤a1≤17
C.2≤a1≤3
D.2≤a1≤6
18.已知四面体ABCD中,棱BC,AD所在直线所成的角为60°,且BC=2,AD=3,∠ACD
120°,则四面体ABCD体积的最大值是
√3
C
9
二、填空题(本大题共4小题,每空3分,共15分。)
19.设等比数列{an}的前n项和为Sn(n∈N),首项a1=3,公比q=2,则a4
20.已知平面向量a,b满足a|=3,|b|=4,且a与b不共线若a+k与a一kb互相垂直,
实数k=▲
21.我国南宋著名数学家秦九韶(约1202—1261)被国外科学史家赞誉
为“他那个民族,那个时代,并且确实也是所有时代最伟大的数学家
之一”.他独立推出了“三斜求积”公式,求法是:“以小斜幂并大斜幂
减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为
实.一为从隅,开平方得积.”把以上这段文字写成从三条边长求三角
B
形面积的公式,就是S=/1|ca2-(+a-=b
(第21题图)
.现如图,已
知平面四边形ABCD中,AD=1,AC=33,∠ADC=120°,AB=√2,BC=2,则平面四边形
ABCD的面积是
22.已知f(x)是定义在R上的偶函数,且在[0,十∞)上单调递增.若对任意x∈R,不等式
f(a+|x-b|)≥f(x|-2|x-11)(a,b∈R)恒成立,则2a2+b2的最小值是▲
三、解答题(本大题共3小题,共31分。)
23.(本题满分10分)已知函数f(x)=sinx+sin(x-x)
(I)求f(0)的值;
(Ⅱ)求函数f(x)的最小正周期;
(Ⅲ)当x∈[0,]时,求函数f(x)的最小值
24.(本题满分10分)如图,已知抛物线C:y2=2x的焦点为F,O为坐
标原点,直线l:y=kx+b与抛物线C相交于A,B两点
(I)当k=1,b=-2时,求证:OA⊥OB;
(Ⅱ)若OA⊥OB,点O关于直线l的对称点为D,求DF的取
值范围
(第24题图)
x2+(2a-4)x+2
25.(题满分11分)设a∈R,已知函数f(x)
+a+
0.
(I)当a=1时,写出f(x)的单调递增区间;
(Ⅱ)对任意x≤2,不等式f(x)≥(a-1)x+2恒成立,求实数a的取值范围
选择题(本大题共18小题,每小题3分,共54分。每小题列出的四个选项中只有一个是符
合题目要求的,不选、多选、错选均不得分。)
题号
5
答案A
题号101112
答案
C
B
A
D
A
二、填空题(本大题共4小题,每空3分,共15分。)
三、解答题(本大题共3小题,共31分。)
23.解:(I)f(0)=sinx33
Ⅱ)因为
f(x)=sinx+y。-0sx、inx
=÷sinx+cosx
-sin(x+-)
所以,函数f(x)的最小正周期为2
(Ⅲ)由已知0≤x≤,
得≤x+≤
所以,当x=号时,函数f()=sm(+)的最小值为
24.解:(I)由方程组
y=x-2
消去y,得x2-6x+4=0
设A(x1,y1),B(x2,y2),
x1+x2=6,x1·x2=4,y1y
因为OA·OB=x1x2+y;y2=0,
所以,OA⊥OB
(Ⅱ)由方程组
yy2k
消去x,得ky2-2y+2b=0(k≠0)
b2
k
k
由OA·OB=x1x2+y1y2
解得
b=-2k或b=0(舍).
设点O关于直线l的对称点D(x0,y0)
k
由方程组
(第24题图)
2
4k
k2+1
得
即
4k2
4k
y
由点F(,0),
得DF|=1/49k+1
2√k2+1
k2+1
由k2>0,
得|DF∈(,)
x2-2x+2,x≤0,
25.解:(1)当a=1时,f(x)={x
所以,f(x)的单调递增区间是(1,+∞)
()若x≤0,ax2+(2a-4)x+2≥(a-1)x+2,
于是ax2+(a-3)x≥0在x∈(-∞,0]上恒成立,
则a=0或
得0≤a≤3.
若x>0,f(x)=-+a+|x-1
当0
所以,a≥-1
∈R
当1
(x=1(2x=12≥a(x-1),
得
所以,a≤
综上所述,0≤a≤1
、选择题(本大题共18小题,每小题3分,共54分。每小题列出的四个选项中只有一个是符
合题目要求的,不选、多选、错选均不得分。)
1.已知集合A=(1,2,3},B={3,4,5,6},则A∩B=
A.{3}
B.{1,2
C.{4,5,6}
D.{1,2,3,4,5,6
2.函数f(x)=loga(4-x)(a>0,且a≠1)的定义域是
A.(0,4)
B.(4,+
D.(-∞,4)U(4,+∞)
3.圆(x-3)2+(y+2)2=16的圆心坐标是
A.(-3,2)
C.(-2,3
4.一元二次不等式x(9-x)>0的解集是
A.{x|x<0或x>9}
B.{x|0
D.{x|-9
A.(0,3),(0,-3)
B.(3,0),(—3,0)
C.(0,√41),(0,-√41)
D.(√41,0),(-√41,0)
6.已知空间向量a=(-1,1,3),b=(2,-2,x),若a∥b,则实数x的值是
4
4
7. cos2
T一S18
A
B
√2
8若实数x,y满足不等式组{x+y≤1,则2x+y的最小值是
A.3
B.
C.0
9.平面a与平面β平行的条件可以是
A.a内有无穷多条直线都与β平行
B.直线a∥a,a∥B,且直线a不在a内,也不在β内
C.直线aCa,直线bCB,且a∥B,b∥a
D.a内的任何直线都与B平行
10,函数f(z)=1x+1+1x-1千的图象大致是
B
D
11.已知两条直线l1:(3+m)x+4y=5-3m,l2:2x+(5+m)y=8,若l1⊥l2,则实数m的
值是
A.-1或-7
B.—7
C.
12.已知某几何体的三视图如图所示,则该几何体的体积是
A.24
B.12
C.8
D.4
13.已知x,y是实数,则“x+y≤1”是“x≤1或y≤1”的
k∈lx∈l
正视图
侧视图
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
俯视图
D.既不充分也不必要条件
(第12题图)
14.已知数列{an}的前n项和为Sn=n2+2n+3(n∈N),则下列结论正确的是
A.数列{an}是等差数列
B.数列{an}是递增数列
C.a1,a5,a成等差数列
D.S6-S3,S-S6,S12-S成等差数列
B
15.如图,正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1的底面边长
为a,侧棱长为2a,则AC1与侧面ABB1A1所成的角是
A.30
B.45°
B
C.60
D.90
(第15题图)
16.如图所示,已知双曲线C:之2y2=1(a>0,b>0)的右焦点为F,双
b2
曲线C的右支上一点A,它关于原点O的对称点为B,满足
∠AFB=120°,且BF|=3AF|,则双曲线C的离心率是
F
B
(第16题图)
D
an+1,n为奇数,
17.已知数列{an}满足an为偶数,
(n∈N),若2≤a10≤3,则a1的取值范围
是
A.1≤a1≤10
B.1≤a1≤17
C.2≤a1≤3
D.2≤a1≤6
18.已知四面体ABCD中,棱BC,AD所在直线所成的角为60°,且BC=2,AD=3,∠ACD
120°,则四面体ABCD体积的最大值是
√3
C
9
二、填空题(本大题共4小题,每空3分,共15分。)
19.设等比数列{an}的前n项和为Sn(n∈N),首项a1=3,公比q=2,则a4
20.已知平面向量a,b满足a|=3,|b|=4,且a与b不共线若a+k与a一kb互相垂直,
实数k=▲
21.我国南宋著名数学家秦九韶(约1202—1261)被国外科学史家赞誉
为“他那个民族,那个时代,并且确实也是所有时代最伟大的数学家
之一”.他独立推出了“三斜求积”公式,求法是:“以小斜幂并大斜幂
减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为
实.一为从隅,开平方得积.”把以上这段文字写成从三条边长求三角
B
形面积的公式,就是S=/1|ca2-(+a-=b
(第21题图)
.现如图,已
知平面四边形ABCD中,AD=1,AC=33,∠ADC=120°,AB=√2,BC=2,则平面四边形
ABCD的面积是
22.已知f(x)是定义在R上的偶函数,且在[0,十∞)上单调递增.若对任意x∈R,不等式
f(a+|x-b|)≥f(x|-2|x-11)(a,b∈R)恒成立,则2a2+b2的最小值是▲
三、解答题(本大题共3小题,共31分。)
23.(本题满分10分)已知函数f(x)=sinx+sin(x-x)
(I)求f(0)的值;
(Ⅱ)求函数f(x)的最小正周期;
(Ⅲ)当x∈[0,]时,求函数f(x)的最小值
24.(本题满分10分)如图,已知抛物线C:y2=2x的焦点为F,O为坐
标原点,直线l:y=kx+b与抛物线C相交于A,B两点
(I)当k=1,b=-2时,求证:OA⊥OB;
(Ⅱ)若OA⊥OB,点O关于直线l的对称点为D,求DF的取
值范围
(第24题图)
x2+(2a-4)x+2
25.(题满分11分)设a∈R,已知函数f(x)
+a+
0.
(I)当a=1时,写出f(x)的单调递增区间;
(Ⅱ)对任意x≤2,不等式f(x)≥(a-1)x+2恒成立,求实数a的取值范围
选择题(本大题共18小题,每小题3分,共54分。每小题列出的四个选项中只有一个是符
合题目要求的,不选、多选、错选均不得分。)
题号
5
答案A
题号101112
答案
C
B
A
D
A
二、填空题(本大题共4小题,每空3分,共15分。)
三、解答题(本大题共3小题,共31分。)
23.解:(I)f(0)=sinx33
Ⅱ)因为
f(x)=sinx+y。-0sx、inx
=÷sinx+cosx
-sin(x+-)
所以,函数f(x)的最小正周期为2
(Ⅲ)由已知0≤x≤,
得≤x+≤
所以,当x=号时,函数f()=sm(+)的最小值为
24.解:(I)由方程组
y=x-2
消去y,得x2-6x+4=0
设A(x1,y1),B(x2,y2),
x1+x2=6,x1·x2=4,y1y
因为OA·OB=x1x2+y;y2=0,
所以,OA⊥OB
(Ⅱ)由方程组
yy2k
消去x,得ky2-2y+2b=0(k≠0)
b2
k
k
由OA·OB=x1x2+y1y2
解得
b=-2k或b=0(舍).
设点O关于直线l的对称点D(x0,y0)
k
由方程组
(第24题图)
2
4k
k2+1
得
即
4k2
4k
y
由点F(,0),
得DF|=1/49k+1
2√k2+1
k2+1
由k2>0,
得|DF∈(,)
x2-2x+2,x≤0,
25.解:(1)当a=1时,f(x)={x
所以,f(x)的单调递增区间是(1,+∞)
()若x≤0,ax2+(2a-4)x+2≥(a-1)x+2,
于是ax2+(a-3)x≥0在x∈(-∞,0]上恒成立,
则a=0或
得0≤a≤3.
同课章节目录
