数学好玩1 密铺 课件(48张ppt)
图片预览











文档简介
课件48张PPT。 用一种或两种以上的图形,将
一个平面既不留空隙,也不重叠地
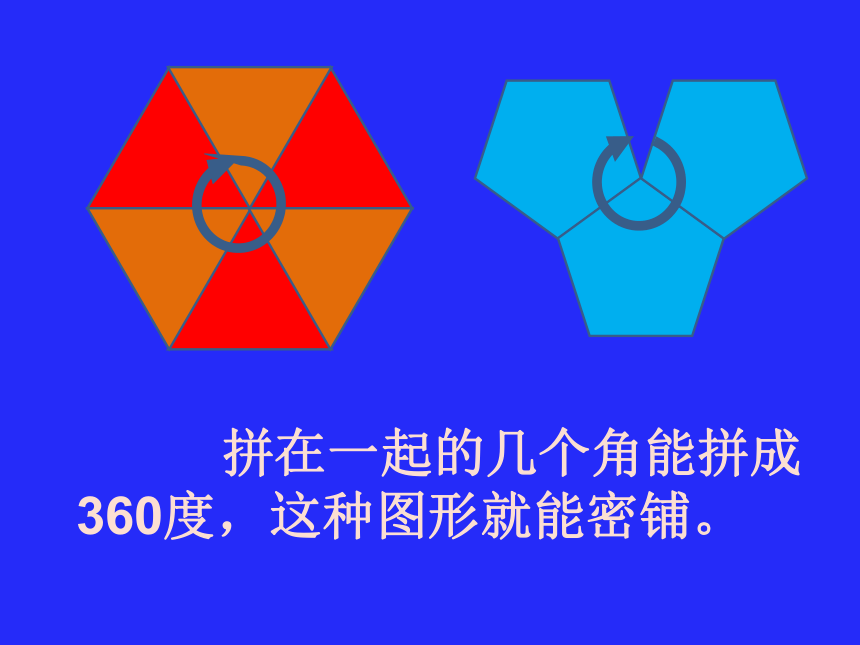
铺满,就是密铺。不留空隙不重叠想一想,它们是密铺吗?用下面的图形可以密铺吗? 拼在一起的几个角能拼成360度,这种图形就能密铺。 能拼成360度,这种图形就能密铺。一个多边形的几个内角拼在一起的几个角1619年,数学家奇柏(J.Kepler)第一个利用正多边形铺嵌平面。1891年,前苏联物理学家费德洛夫(E.S.Fedorov)发现了十七种不同的铺嵌平面的对称图案。1924年,数学家波利亚(Polya)和尼格利(Nigele)重新发现这个事实。波利亚尼格利作品最富趣味的是荷兰艺术家埃舍尔(M.C.Escher)与密铺。他到西班牙旅行参观时,对一种名为阿罕拉(Alhambra)的建筑物有很深的印象,这是一种十三世纪皇宫建筑物,其墙身、地板和天花板由摩尔人建造,而且铺了种类繁多、美仑美奂的马赛克图案。 Escher用数日
的时间复制了这
些图案,并得到
了启发,创造了
各种并不局限于
几何图案的密铺
图案,这些图案
包括人、青蛙、
鱼、鸟、蜥蜴,
甚至是他凭空想
象的物体。他创
作的艺术作品,
结合数学与艺术,让人对数学产生了另一种看法。建筑中的密铺密铺图案 自己动手,设计一幅
密铺图案。
一个平面既不留空隙,也不重叠地
铺满,就是密铺。不留空隙不重叠想一想,它们是密铺吗?用下面的图形可以密铺吗? 拼在一起的几个角能拼成360度,这种图形就能密铺。 能拼成360度,这种图形就能密铺。一个多边形的几个内角拼在一起的几个角1619年,数学家奇柏(J.Kepler)第一个利用正多边形铺嵌平面。1891年,前苏联物理学家费德洛夫(E.S.Fedorov)发现了十七种不同的铺嵌平面的对称图案。1924年,数学家波利亚(Polya)和尼格利(Nigele)重新发现这个事实。波利亚尼格利作品最富趣味的是荷兰艺术家埃舍尔(M.C.Escher)与密铺。他到西班牙旅行参观时,对一种名为阿罕拉(Alhambra)的建筑物有很深的印象,这是一种十三世纪皇宫建筑物,其墙身、地板和天花板由摩尔人建造,而且铺了种类繁多、美仑美奂的马赛克图案。 Escher用数日
的时间复制了这
些图案,并得到
了启发,创造了
各种并不局限于
几何图案的密铺
图案,这些图案
包括人、青蛙、
鱼、鸟、蜥蜴,
甚至是他凭空想
象的物体。他创
作的艺术作品,
结合数学与艺术,让人对数学产生了另一种看法。建筑中的密铺密铺图案 自己动手,设计一幅
密铺图案。
