3.2正比例 课件(19张ppt)
图片预览






文档简介
课件19张PPT。西师版小学六年级数学下册
正比例的意义教学目标 1.理解正比例的意义,能够根据正比例的意义判断两种量是不是成正比例。
2.初步培养同学们用事物相互联系和发展变化的观点来分析问题。
3.初步渗透函数思想。
复习:观察有哪些量?写出等量关系式?1、小刚2小时行了240千米。问题:平均每小时行了多少千米?有“时间”和“路程”两个量,叫已知量。怎么计算:240÷ 2 =120(千米)关系式: 路程÷时间=速度复习2:观察有哪些量?写出等量关系式?2、输入360个字用了4分钟。问题:平均每分钟打了多少个字?有“工作总量”和“工作时间”两个量,叫已知量。怎么计算:360÷ 4 =90(个)关系式:工作总量÷工作时间=工作效率关系式:
工作总量÷工作时间=工作效率
路程 ÷ 时间 = 速度
还有:总价÷数量=单价 等这些都是我们以前学习过的常见的数量关系式,
各数量关系之间是相互联系的,数量与数量之间
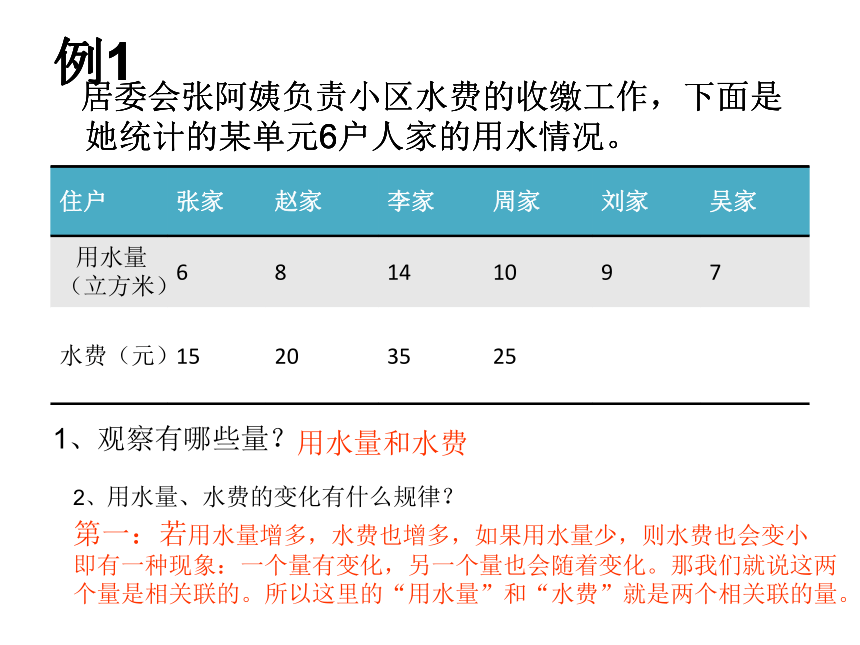
有关联。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。2、用水量、水费的变化有什么规律?第一:若用水量增多,水费也增多,如果用水量少,则水费也会变小
即有一种现象:一个量有变化,另一个量也会随着变化。那我们就说这两
个量是相关联的。所以这里的“用水量”和“水费”就是两个相关联的量。1、观察有哪些量?用水量和水费例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。先回答:你能写出哪些比? 你能提出什么数学问题?那么请问:15:6的比值是?这个比值表示什么?能写出比:15:6 20:8等等,求每立方水的单价?4、表中有哪个量是固定不变的?再观察:20:8的比值,35:14的比值,它们有什么特点?15:6的比值是2.5,而15:6可以写成15÷6,意思是水费÷用水量,那么15÷6=2.5,这个比值“2.5”其实就是“单价”!例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例14、表中有哪个量是固定不变的?通过观察:水费
用水量 =—==……=—=2.5水费与用水量的比值就是 单价那么哪个量不变?说明单价是固定的量即”单价不变“,我们通常就说”单价一定”5、你能写出关系式吗?特点:水费用水量=单价(一定)就是两个量的比值固定不变 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。用水量水费例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。单价(一定)=水费用水量6、现在你能把表格补充完整吗?
是根据什么来完成的?根据前面计算它们的比值,我们可以得出比值都是2.5,即
单价是不变的。所以,我们在填空的时候,就可以用单价
(2.5)来参与计算。单价×数量=总价先想:我们应该求什么量?试一试: 小明在乘车旅行的途中,根据汽车仪表盘记录了下面的数据。 根据发现的规律,在表中空白处填上适当的数什么规律?首先有两个量,路程和时间。这两个量的比的比值
表示的是速度。即 路程:时间= 速度,而且
比值”速度“是固定不变的!比值为:80 就是说速度都是80. 根据比值,相当于就告诉了两个条件,原来有路程,现在又知道了速度,能不能求 时间? 怎么计算?关系式为? 第二个规律:如果一个量变大,另一个量也随着变大,一个量如果变小,那另一个量也会随着变小。议一议 小组讨论解决 从上面的两个实例中,你发现了什么?
1、一般都有两个量,就像用水量和水费、时间和路程等这样相关联的两个量,而且这两个量会相互变化,一种量扩大或缩小若干倍,另一种量也会随着扩大或缩小相同的倍数。议一议 小组讨论解决2 、两个相关联的量组成的比的比值是固定不变的,总是一定的!课堂小结1 用水量和水费,时间和路程分别是两种相关量;在水费和用水量这两种量中,相对应的两个量的比值是一定的;时间和路程的比值也是一个定值。
一种量扩大或缩小,另一种量也扩大或缩小相同的倍数。
像上面的用水量和水费,时间和路程这样的两种量,它们得比值一定,这样的两种量叫成正比例的量,它们的关系叫做正比例关系。
怎么快速的判断两个量是否成正比例?关键看两个方面:1、两个量的比值是固定不变的2、两个量会相互变化,一个变大,另一个也会变大扩展应用1:1、举一个正比例例子(先自己举例,写在本子上,再集体交流。)
2、思考:明明三岁时体重12千克,十一岁时体重44千克。于是小张就说:“明明的体重和身高成正比例。”你认为小张的说法对吗?为什么?扩展应用2:练习:已知A和B成正比例,完成下表。扩展应用3: 判断下面每题中的两种量是不是成正比例,并说明理由。
1.每包书中册数相同,包数和总册数。
2.全班的学生人数一定,每组的人数和组数。
3.房间地面面积一定,房间里的人数和每人所占的面积。
4.和一定,加数和另一个加数。
5.一个人的年龄和他的体重。扩展应用4: 现在某体育用品店声称:如果买50只篮球以下,每只42元;如果买50只篮球以上(包括50只),每只40元。请问总价同篮球的数量是不是成正比例,如果成 正比例,那是 在什么情况?
例2 锦江机械厂新研制出了一种面粉及,工人在使用的过程中收集到下面一些数据。面粉的质量和小麦的质量成正比例关系,他们的关系可以用图像来表示。面粉的质量和小麦的质量的关系图 0 50 100 150 200 250 300 350 400 450 500 550 600 650 700小麦质量(kg)面粉质量(kg)探索问题:观察上图,你发现了什么?
王大爷家有500kg小麦,如果全部加工,能磨出多少千克面粉?
根据图像估计一下,要磨出300kg面粉,大约需要多少千克小麦?
复习:观察有哪些量?写出等量关系式?1、小刚2小时行了240千米。问题:平均每小时行了多少千米?有“时间”和“路程”两个量,叫已知量。怎么计算:240÷ 2 =120(千米)关系式: 路程÷时间=速度复习2:观察有哪些量?写出等量关系式?2、输入360个字用了4分钟。问题:平均每分钟打了多少个字?有“工作总量”和“工作时间”两个量,叫已知量。怎么计算:360÷ 4 =90(个)关系式:工作总量÷工作时间=工作效率关系式:
工作总量÷工作时间=工作效率
路程 ÷ 时间 = 速度
还有:总价÷数量=单价 等这些都是我们以前学习过的常见的数量关系式,
各数量关系之间是相互联系的,数量与数量之间
有关联。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。2、用水量、水费的变化有什么规律?第一:若用水量增多,水费也增多,如果用水量少,则水费也会变小
即有一种现象:一个量有变化,另一个量也会随着变化。那我们就说这两
个量是相关联的。所以这里的“用水量”和“水费”就是两个相关联的量。1、观察有哪些量?用水量和水费例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。先回答:你能写出哪些比? 你能提出什么数学问题?那么请问:15:6的比值是?这个比值表示什么?能写出比:15:6 20:8等等,求每立方水的单价?4、表中有哪个量是固定不变的?再观察:20:8的比值,35:14的比值,它们有什么特点?15:6的比值是2.5,而15:6可以写成15÷6,意思是水费÷用水量,那么15÷6=2.5,这个比值“2.5”其实就是“单价”!例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例14、表中有哪个量是固定不变的?通过观察:水费
用水量 =—==……=—=2.5水费与用水量的比值就是 单价那么哪个量不变?说明单价是固定的量即”单价不变“,我们通常就说”单价一定”5、你能写出关系式吗?特点:水费用水量=单价(一定)就是两个量的比值固定不变 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。用水量水费例1 居委会张阿姨负责小区水费的收缴工作,下面是她统计的某单元6户人家的用水情况。单价(一定)=水费用水量6、现在你能把表格补充完整吗?
是根据什么来完成的?根据前面计算它们的比值,我们可以得出比值都是2.5,即
单价是不变的。所以,我们在填空的时候,就可以用单价
(2.5)来参与计算。单价×数量=总价先想:我们应该求什么量?试一试: 小明在乘车旅行的途中,根据汽车仪表盘记录了下面的数据。 根据发现的规律,在表中空白处填上适当的数什么规律?首先有两个量,路程和时间。这两个量的比的比值
表示的是速度。即 路程:时间= 速度,而且
比值”速度“是固定不变的!比值为:80 就是说速度都是80. 根据比值,相当于就告诉了两个条件,原来有路程,现在又知道了速度,能不能求 时间? 怎么计算?关系式为? 第二个规律:如果一个量变大,另一个量也随着变大,一个量如果变小,那另一个量也会随着变小。议一议 小组讨论解决 从上面的两个实例中,你发现了什么?
1、一般都有两个量,就像用水量和水费、时间和路程等这样相关联的两个量,而且这两个量会相互变化,一种量扩大或缩小若干倍,另一种量也会随着扩大或缩小相同的倍数。议一议 小组讨论解决2 、两个相关联的量组成的比的比值是固定不变的,总是一定的!课堂小结1 用水量和水费,时间和路程分别是两种相关量;在水费和用水量这两种量中,相对应的两个量的比值是一定的;时间和路程的比值也是一个定值。
一种量扩大或缩小,另一种量也扩大或缩小相同的倍数。
像上面的用水量和水费,时间和路程这样的两种量,它们得比值一定,这样的两种量叫成正比例的量,它们的关系叫做正比例关系。
怎么快速的判断两个量是否成正比例?关键看两个方面:1、两个量的比值是固定不变的2、两个量会相互变化,一个变大,另一个也会变大扩展应用1:1、举一个正比例例子(先自己举例,写在本子上,再集体交流。)
2、思考:明明三岁时体重12千克,十一岁时体重44千克。于是小张就说:“明明的体重和身高成正比例。”你认为小张的说法对吗?为什么?扩展应用2:练习:已知A和B成正比例,完成下表。扩展应用3: 判断下面每题中的两种量是不是成正比例,并说明理由。
1.每包书中册数相同,包数和总册数。
2.全班的学生人数一定,每组的人数和组数。
3.房间地面面积一定,房间里的人数和每人所占的面积。
4.和一定,加数和另一个加数。
5.一个人的年龄和他的体重。扩展应用4: 现在某体育用品店声称:如果买50只篮球以下,每只42元;如果买50只篮球以上(包括50只),每只40元。请问总价同篮球的数量是不是成正比例,如果成 正比例,那是 在什么情况?
例2 锦江机械厂新研制出了一种面粉及,工人在使用的过程中收集到下面一些数据。面粉的质量和小麦的质量成正比例关系,他们的关系可以用图像来表示。面粉的质量和小麦的质量的关系图 0 50 100 150 200 250 300 350 400 450 500 550 600 650 700小麦质量(kg)面粉质量(kg)探索问题:观察上图,你发现了什么?
王大爷家有500kg小麦,如果全部加工,能磨出多少千克面粉?
根据图像估计一下,要磨出300kg面粉,大约需要多少千克小麦?
