人教版七年级下册9.2 实际问题与一元一次不等式课件 (共31张PPT)
文档属性
| 名称 | 人教版七年级下册9.2 实际问题与一元一次不等式课件 (共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-06 00:00:00 | ||
图片预览










文档简介
课件31张PPT。我店累计购买100元商品后,再购买的商品按原价的90%收费甲我店累计购买50元商品后,再购买的商品按原价的95%收费乙 解:当购买40元商品时,两个商店购物花费没有区别.
当购买80元商品时,在乙店购物比较优惠.
当购买140元商品时,
甲店:100+40×90%=136(元)
乙店:50+90 ×95%=135.5(元)
在乙店购物比较优惠.(1)如果你要分别购买40元、80 元、140元商
品,应该去哪家商店更优惠? 解:设累计购物x元(x>100),如果在乙店购物花费小,则50+0.95(x-50) <100+0.9(x-100)去括号,得:50+0.95x-47.5<100+0.9x-90移项且合并同类项,得0.05x<7.5系数化为1,得x<150 ∴累计购物超过100元不超过150元时在乙店购物比较优惠. (2)如果累计购物超过100元,在乙店购物比较
优惠吗? 1.会根据实际问题中的数量关系建立数学模型,会用一元一次不等式解决实际问题; 2.初步感知实际问题对不等式解集的影响,培养数学建模能力和分析问题、解决问题的能力.知识与能力 1.通过观察、实践、讨论等活动,经历从实际中抽象出数学模型的过程,积累利用一元一次不等式解决实际问题的经验,渗透分类讨论思想,感知方程与不等式的内在联系; 2.通过去分母的方法解一元一次不等式,了解数学中的化归思想,感知不等式与方程的内在联系.过程与方法 1.在积极参与数学学习活动的过程中,初步认识一元一次不等式的应用价值,形成实事求是的态度和独立思考的习惯; 2.通过开放性问题的设计,增强创新意识和挑战自我意识,激发学习兴趣; 3.结合实际,提高学习兴趣.在活动中获得成功的体验,激发起求知的欲望,增强学习的自信心.情感态度与价值观 1.寻找实际问题中的不等关系,建立数学模型;
2.如何建立不等式关系,并根据不等关系列出不等式;
3.根据题意,分析各类问题中的数量关系,会熟练列不等式解应用问题.重点 1.弄清列不等式解决实际问题的思想方法,用去括号法解一元一次不等式;
2.在实际问题中如何建立不等关系,并根据不等关系列出不等式;
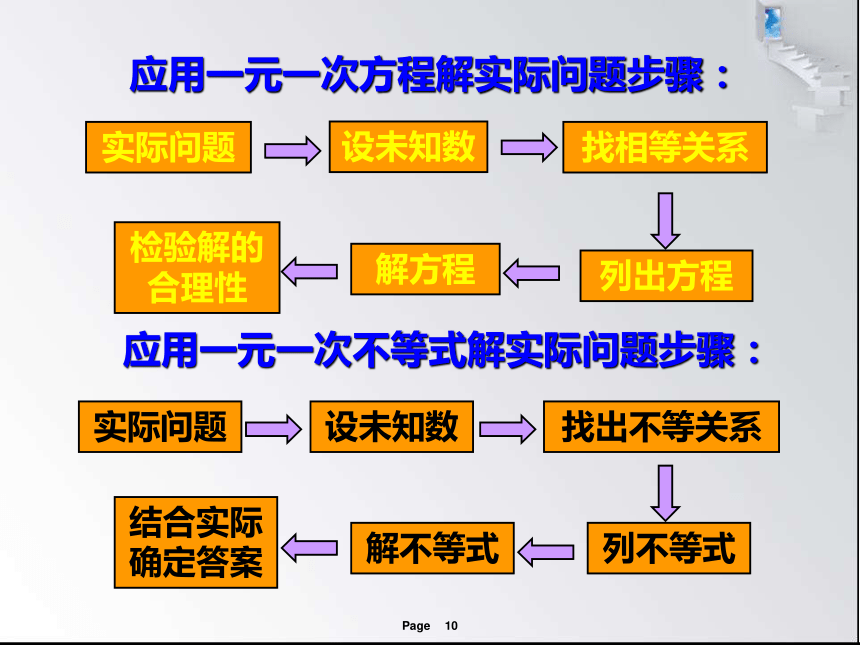
3.把生活中的实际问题抽象为数学问题.难点实际问题应用一元一次不等式解实际问题步骤:实际问题应用一元一次方程解实际问题步骤:运用不等式解实际问题的一般步骤:明确不等关系的词语的联系与区别.(如:‘‘不超过” 、“至少”等词语的含义)(2)设元---选合适的量为未知数.(3)列不等式(组)---选与未知数相关的不等关系.(4)解不等式(组)---根据不等式的性质.(5)解答---利用不等式(组)的解,写出符合题意的结果.(1)审题--- 例1 2002年北京空气质量良好(二级以上)的天数与全年天数之比达到55%,如果到2008年这样的比值要超过70%,那么2008年空气质量良好的天数要比2002年至少增加多少? 解:设2008年北京空气质量良好的天数比2002年增加x天,2002年有365×0.55天空气质量良好,2008年有(x+365×0.55)天空气质量良好,并且去分母,得 x+200.75>256.2移项,合并,得 x>55.45由x应为正整数,得x≥56 答:2008年空气质量良好的天数至少比2002年增加56天,才能使这一年空气质量良好的天数超过全年天数的70% 例2 几个同学合影留念,每人交了0.60元分到一张照片.已知一张彩色底片0.58元,扩印一张相片0.40元,在将收来的钱尽量用掉的前提下,这张相片上的同学最少有几人? 解:设这张相片上的同学有x人,根据题意,得0.60x≥0.58+0.40x解得x≥2.9∵x为正整数,∴x=3答:这张相片上的同学最少有3人. 例3 电脑公司销售一批计算机,第一个月以每台5500元的价格出售80台,第二个月降价后以每台5000元的价格将这批计算机全部售出,销售款总量超过66万元.这批计算机最少有多少台? 解:设这批计算机有x台,根据题意,得
5500×80+5000(x-80)>660000
440000+5000x-400000>660000
5000x>620000
x>124
根据实际x应为不小于125的正整数,x=125,
答:这批计算机最少有125台. 例4 某次知识竞赛共有20道题, 每一题答对得10分,答错或不答都扣5分, 小明得分要超过90分,他至少要答对多少道题? 解:设小明答对x道题,则他答错或不答的题数为20-x,根据他的得分要超过90,得
10x-5(20-x) ≥90解这个不等式,得
10 x -100+5x> 90依题意,x应是整数而且不能超过20.15x>190答:小明至少要答对13道题. 例5 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答,一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小答对了x道题,根据题意,得
4x-(25-x) ≥85
解得: x≥22
答:小明至少答对了22道题. 例6 某单位计划在新年期间组织员工到某地旅游,参如旅游的的人数估计为12~27人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一家旅行社,支付的旅游费用较少? 解:设该单位参加这次旅游的人数是x人, 选择甲旅行社时,所需的费用为200×0.75x ,即150x. 选择乙旅行社时,所需的费用为200×0.8(x-1),即160x-160.
当150x=160x-160时, 解得x=16;
当150x>160x-160时, 解得x<16;
当150x<160x-160时, 解得x>16;
答:当人数为16人时,甲、乙两家旅行社的收费相同;
当人数为17~27人时,选择甲旅行社费用较少;
当人数为12~15人时,选择乙旅行社费用较少. 例7【温州.99】某校师生组织学生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可少租一辆,且余30个座位.
(1)求该校参加春游人数;
(2)已知45座客车租金为每辆250元,60座客车的租金为每辆300元.
问:①单独租用一种车各需租金多少元?
②这次春游同时租用这两种客车,其中60座客车比45座客车多租1辆,所用租金比单独租用一种客车要节省,按这种方案需用租金多少元? (2)①由(1)知,单独租用45座需 6辆,单独租用60座需5辆.
②由题知,单独租45座或60座客车需费用均为1500元.设该校租用45座客车y辆,则租用60座客车(y+1)辆.由题意,可得 250y+300(y+1)<1500,解得 y<2.18
因为y是正整数,∴y=1或y=2,
y=1时,只能乘坐45×1+60×2=165<270人,舍去.
∴y=2,此时可乘坐45×2+60×3=270人,正好;
费用为250×2+300×3=1400元.
答:该校租45座客车2辆,60座客车3辆最省钱,花费1400元. 应用一元一次不等式解实际问题的一般步骤:实际问题
(包含不等关系)数学问题
(一元一次不等式)数学问题的解
(不等式的解集)实际问题
的解答设未知数,
列不等式检验解不等式1.在一次知识竞赛中,有10道抢答题,答对一题
得10分,答错一题扣5分,不答得0分,小丽有
一道题没有答,成绩仍然没有低于60分,她至
少答对几道题? 解:设小丽答对的题数是x,则答错的题数是9-x,根据题意,得
10x-5(9-x) ≥60解这个不等式,得 x ≥ 7答:她至少答对7道题.2.刘刚准备用30元买钢笔和笔记本,已知一支钢
笔4.5元,一本笔记本3元,如果刘刚钢笔和笔
记本共买了8件,则他有多少种购买方案? 解:设他可以买x支钢笔,则笔记本为(8-x)个,由题意,得4.5x+3(8-x)≤30解得x≤4∴x=4或3或2或1∵x为正整数, 答:刘刚有4种购买方案, ①4支钢笔和4本笔记本, ② 3支钢笔和5本笔记本,③ 2支钢笔和6本笔记本, ④ 1支钢笔和7本笔记本.解这个不等式,得:2x+3 ×4≤20 2x ≤ 8答:他最多还能买4根火腿肠.解:设他还可买X根火腿肠.根据题意,得x ≤ 43.乐乐准备用20元钱买火腿肠和方便面.已知
一根火腿肠2元钱,一盒方便面3元钱,他买
了4盒方便面,问他最多还能买多少根火腿
肠?4.甲、乙两地相距30km,刘迪从甲地去乙地,以
6km/h的行驶速度可按时到达,现刘迪走了3.5 h
后,因事停留半小时,为了按时到达,刘迪后来
的速度至少是多少?解:设刘迪后来的速度是xkm/h.根据题意,得
3.5×6+(30÷6-3.5-0.5)x ≥30.
解得x≥9.
答:刘迪后来的速度至少是9km/ h.5.商场出售的A型冰箱每台售价2500元,每日耗电
量为1度,而B种节能冰箱每台售价虽比A型冰箱
高出10%,但每日耗电量却为0.5度,现将A型冰
箱打折出售,问商场至少打几折,消费者购买才
合算?(按使用期为10年,每年365天,每度电
0.70元计算).解:设商场打x折.根据题意,得
x×2500+365×10 ×0.70
≤2500×(1+10%)+365×10 ×0.5×0.70
解得x ≤0.585.
答:商场至少打5.85折,消费者购买才合算.5.设售出自行车x辆.
275x>250×200,x≥182.
6.设导火线长xcm,7.设前年全厂年利润是x万元.8.设售价定为每千克x元时不亏本.
0.95x≥15,x≥1.58.
9.设这批电脑有x台.
5 500×60+5 000(x-60)>550 000,
x>104,x≥105.
10.2<x<4.
11.3x-1=2n(n是正整数),
当购买80元商品时,在乙店购物比较优惠.
当购买140元商品时,
甲店:100+40×90%=136(元)
乙店:50+90 ×95%=135.5(元)
在乙店购物比较优惠.(1)如果你要分别购买40元、80 元、140元商
品,应该去哪家商店更优惠? 解:设累计购物x元(x>100),如果在乙店购物花费小,则50+0.95(x-50) <100+0.9(x-100)去括号,得:50+0.95x-47.5<100+0.9x-90移项且合并同类项,得0.05x<7.5系数化为1,得x<150 ∴累计购物超过100元不超过150元时在乙店购物比较优惠. (2)如果累计购物超过100元,在乙店购物比较
优惠吗? 1.会根据实际问题中的数量关系建立数学模型,会用一元一次不等式解决实际问题; 2.初步感知实际问题对不等式解集的影响,培养数学建模能力和分析问题、解决问题的能力.知识与能力 1.通过观察、实践、讨论等活动,经历从实际中抽象出数学模型的过程,积累利用一元一次不等式解决实际问题的经验,渗透分类讨论思想,感知方程与不等式的内在联系; 2.通过去分母的方法解一元一次不等式,了解数学中的化归思想,感知不等式与方程的内在联系.过程与方法 1.在积极参与数学学习活动的过程中,初步认识一元一次不等式的应用价值,形成实事求是的态度和独立思考的习惯; 2.通过开放性问题的设计,增强创新意识和挑战自我意识,激发学习兴趣; 3.结合实际,提高学习兴趣.在活动中获得成功的体验,激发起求知的欲望,增强学习的自信心.情感态度与价值观 1.寻找实际问题中的不等关系,建立数学模型;
2.如何建立不等式关系,并根据不等关系列出不等式;
3.根据题意,分析各类问题中的数量关系,会熟练列不等式解应用问题.重点 1.弄清列不等式解决实际问题的思想方法,用去括号法解一元一次不等式;
2.在实际问题中如何建立不等关系,并根据不等关系列出不等式;
3.把生活中的实际问题抽象为数学问题.难点实际问题应用一元一次不等式解实际问题步骤:实际问题应用一元一次方程解实际问题步骤:运用不等式解实际问题的一般步骤:明确不等关系的词语的联系与区别.(如:‘‘不超过” 、“至少”等词语的含义)(2)设元---选合适的量为未知数.(3)列不等式(组)---选与未知数相关的不等关系.(4)解不等式(组)---根据不等式的性质.(5)解答---利用不等式(组)的解,写出符合题意的结果.(1)审题--- 例1 2002年北京空气质量良好(二级以上)的天数与全年天数之比达到55%,如果到2008年这样的比值要超过70%,那么2008年空气质量良好的天数要比2002年至少增加多少? 解:设2008年北京空气质量良好的天数比2002年增加x天,2002年有365×0.55天空气质量良好,2008年有(x+365×0.55)天空气质量良好,并且去分母,得 x+200.75>256.2移项,合并,得 x>55.45由x应为正整数,得x≥56 答:2008年空气质量良好的天数至少比2002年增加56天,才能使这一年空气质量良好的天数超过全年天数的70% 例2 几个同学合影留念,每人交了0.60元分到一张照片.已知一张彩色底片0.58元,扩印一张相片0.40元,在将收来的钱尽量用掉的前提下,这张相片上的同学最少有几人? 解:设这张相片上的同学有x人,根据题意,得0.60x≥0.58+0.40x解得x≥2.9∵x为正整数,∴x=3答:这张相片上的同学最少有3人. 例3 电脑公司销售一批计算机,第一个月以每台5500元的价格出售80台,第二个月降价后以每台5000元的价格将这批计算机全部售出,销售款总量超过66万元.这批计算机最少有多少台? 解:设这批计算机有x台,根据题意,得
5500×80+5000(x-80)>660000
440000+5000x-400000>660000
5000x>620000
x>124
根据实际x应为不小于125的正整数,x=125,
答:这批计算机最少有125台. 例4 某次知识竞赛共有20道题, 每一题答对得10分,答错或不答都扣5分, 小明得分要超过90分,他至少要答对多少道题? 解:设小明答对x道题,则他答错或不答的题数为20-x,根据他的得分要超过90,得
10x-5(20-x) ≥90解这个不等式,得
10 x -100+5x> 90依题意,x应是整数而且不能超过20.15x>190答:小明至少要答对13道题. 例5 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答,一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小答对了x道题,根据题意,得
4x-(25-x) ≥85
解得: x≥22
答:小明至少答对了22道题. 例6 某单位计划在新年期间组织员工到某地旅游,参如旅游的的人数估计为12~27人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一家旅行社,支付的旅游费用较少? 解:设该单位参加这次旅游的人数是x人, 选择甲旅行社时,所需的费用为200×0.75x ,即150x. 选择乙旅行社时,所需的费用为200×0.8(x-1),即160x-160.
当150x=160x-160时, 解得x=16;
当150x>160x-160时, 解得x<16;
当150x<160x-160时, 解得x>16;
答:当人数为16人时,甲、乙两家旅行社的收费相同;
当人数为17~27人时,选择甲旅行社费用较少;
当人数为12~15人时,选择乙旅行社费用较少. 例7【温州.99】某校师生组织学生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可少租一辆,且余30个座位.
(1)求该校参加春游人数;
(2)已知45座客车租金为每辆250元,60座客车的租金为每辆300元.
问:①单独租用一种车各需租金多少元?
②这次春游同时租用这两种客车,其中60座客车比45座客车多租1辆,所用租金比单独租用一种客车要节省,按这种方案需用租金多少元? (2)①由(1)知,单独租用45座需 6辆,单独租用60座需5辆.
②由题知,单独租45座或60座客车需费用均为1500元.设该校租用45座客车y辆,则租用60座客车(y+1)辆.由题意,可得 250y+300(y+1)<1500,解得 y<2.18
因为y是正整数,∴y=1或y=2,
y=1时,只能乘坐45×1+60×2=165<270人,舍去.
∴y=2,此时可乘坐45×2+60×3=270人,正好;
费用为250×2+300×3=1400元.
答:该校租45座客车2辆,60座客车3辆最省钱,花费1400元. 应用一元一次不等式解实际问题的一般步骤:实际问题
(包含不等关系)数学问题
(一元一次不等式)数学问题的解
(不等式的解集)实际问题
的解答设未知数,
列不等式检验解不等式1.在一次知识竞赛中,有10道抢答题,答对一题
得10分,答错一题扣5分,不答得0分,小丽有
一道题没有答,成绩仍然没有低于60分,她至
少答对几道题? 解:设小丽答对的题数是x,则答错的题数是9-x,根据题意,得
10x-5(9-x) ≥60解这个不等式,得 x ≥ 7答:她至少答对7道题.2.刘刚准备用30元买钢笔和笔记本,已知一支钢
笔4.5元,一本笔记本3元,如果刘刚钢笔和笔
记本共买了8件,则他有多少种购买方案? 解:设他可以买x支钢笔,则笔记本为(8-x)个,由题意,得4.5x+3(8-x)≤30解得x≤4∴x=4或3或2或1∵x为正整数, 答:刘刚有4种购买方案, ①4支钢笔和4本笔记本, ② 3支钢笔和5本笔记本,③ 2支钢笔和6本笔记本, ④ 1支钢笔和7本笔记本.解这个不等式,得:2x+3 ×4≤20 2x ≤ 8答:他最多还能买4根火腿肠.解:设他还可买X根火腿肠.根据题意,得x ≤ 43.乐乐准备用20元钱买火腿肠和方便面.已知
一根火腿肠2元钱,一盒方便面3元钱,他买
了4盒方便面,问他最多还能买多少根火腿
肠?4.甲、乙两地相距30km,刘迪从甲地去乙地,以
6km/h的行驶速度可按时到达,现刘迪走了3.5 h
后,因事停留半小时,为了按时到达,刘迪后来
的速度至少是多少?解:设刘迪后来的速度是xkm/h.根据题意,得
3.5×6+(30÷6-3.5-0.5)x ≥30.
解得x≥9.
答:刘迪后来的速度至少是9km/ h.5.商场出售的A型冰箱每台售价2500元,每日耗电
量为1度,而B种节能冰箱每台售价虽比A型冰箱
高出10%,但每日耗电量却为0.5度,现将A型冰
箱打折出售,问商场至少打几折,消费者购买才
合算?(按使用期为10年,每年365天,每度电
0.70元计算).解:设商场打x折.根据题意,得
x×2500+365×10 ×0.70
≤2500×(1+10%)+365×10 ×0.5×0.70
解得x ≤0.585.
答:商场至少打5.85折,消费者购买才合算.5.设售出自行车x辆.
275x>250×200,x≥182.
6.设导火线长xcm,7.设前年全厂年利润是x万元.8.设售价定为每千克x元时不亏本.
0.95x≥15,x≥1.58.
9.设这批电脑有x台.
5 500×60+5 000(x-60)>550 000,
x>104,x≥105.
10.2<x<4.
11.3x-1=2n(n是正整数),
