3.4正比例和反比例整理与复习 课件(18张ppt)
文档属性
| 名称 | 3.4正比例和反比例整理与复习 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 116.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-06 00:00:00 | ||
图片预览






文档简介
课件18张PPT。正比例与反比例 一:复习准备1:怎样的两个量是成正比例的量?什么是正比例关系?用字母应如何表示?
2:怎样的两个量是成反比例的量?什么是反比例关系?用字母应如何表示?
1: 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用 来表示两种相关联的量,用字母 表示它们的比值(一定),正比例关系可以表示为:
2: 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用 来表示两种相关联的量,用字母 表示它们的积(一定),反比例关系可以表示为:
3:判断下面每题中两种量成正比例还是成反比例 (1) 单价一定,数量和总价
(2) 路程一定,速度和时间
(3) 工作时间一定,工作总量和工作效率
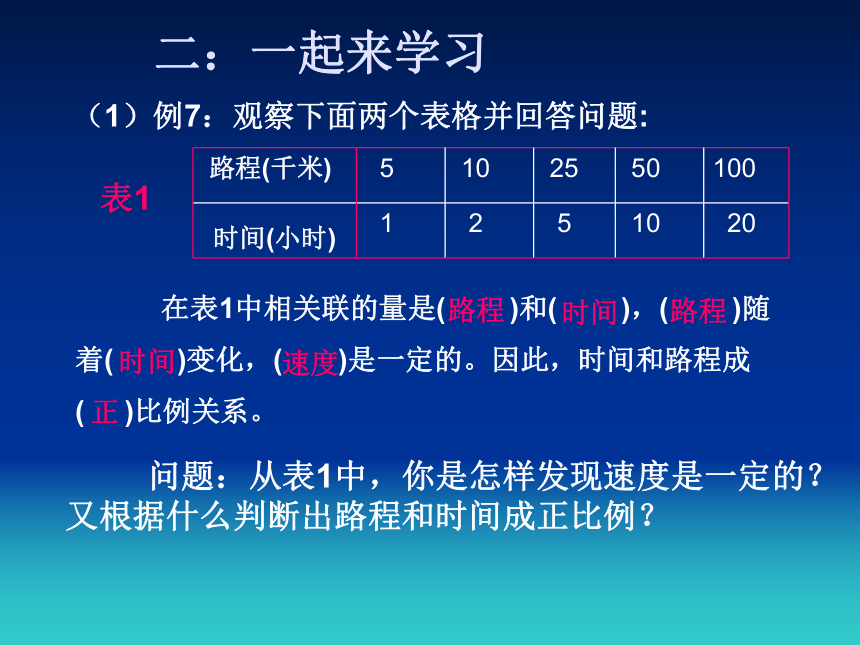
(4) 长方形的面积一定,长和宽 (成正比例)(成反比例)(成正比例)(成反比例) 在表1中相关联的量是( )和( ),( )随着( )变化,( )是一定的。因此,时间和路程成( )比例关系。二:一起来学习(1)例7:观察下面两个表格并回答问题:
表1 路程路程时间 速度正时间 问题:从表1中,你是怎样发现速度是一定的?又根据什么判断出路程和时间成正比例?
表2 在表2中相关联的量是( )和( ),( )随着( )变化,( )是一定的。因此,时间和速度成( )比例关系。速度时间路程时间速度反 问题:从表2中,你是怎样发现路程是一定的?又根据什么判断出时间和速度成反比例?关系是:当路程一定时,速度和时间成反比例。 当时间一定时,路程和速度成正比例。 当速度一定时,路程和时间成正比例。 问题: 路程,速度和时间这三种量之间有怎样的关系?当其中的一个量一定时,其它的两个量存在怎样的比例关系?(2)动脑想一下:(3)细心比一比:1 、都是两种相关联的量
2 、一种量变化,另一种量也随着变化 1 、“变化方向”相同,一种量扩大或缩小,另一种量也随着扩大或缩小。
2 、相对应的两个数的比值(商)是一定的。 1 、“变化方向”相反,一种量缩小或扩大,另一种量反而随着扩大或缩小。
2 、相对应的两个数的积是一定的。跟我学技巧:
正比反比两同胞,两点相同要记牢。首先必是关联量,一量随着另量变。比值一定成正比,乘积一定成反比。 三:巩固练习1:判断单价、数量和总价中一种量一定时,另外两种量成什么比例关系?为什么?
(1)单价一定,数量和总价 ( )
(2)总价一定,数量和单价 ( )
(3)数量一定,总价和单价 ( )成正比例 成正比例 成反比例 有三种!
面积一定时,长和宽成反比例。
长一定时,面积和宽成正比例。
宽一定时,面积和长成正比例。2:从长方形的长、宽和面积三种量中,你能找出几种比例关系?
3:已知x和y成正比例,试填下表并根据表中的数据列出两个比例式:
4:已知当 一定时, 和 成( )比例
当 一定时, 和 成( )比例
当 一定时, 和 成( )比例31652478:2=12:3 16:4=20:5正正反四:课堂小结 今天我们学习了那些知识?你学会了吗?五:活动探究1:正方形的面积和边长是否成比例?为什么?
2:圆的面积和半径是否成比例?为什么?
a
2、根据下列条件,列出等式。(1)用一批纸装订练习本,每本30页,可装订200本,
每本50页,可装订120本。(2)火车从甲地到乙地,每小时行驶30千米,
8小时到达。如果要6小时到达,每小时
必须行驶40千米。(3)读一本书,每天读20页,6天可以读完,
如果每天读5页,需要x天读完。30×1200=50×120 30×8=40×620×6=5x例题: -艘货轮每小时航行20千米,6小时可以到达
目的地。如果要5小时到达,每小时应航行多少千米? 如果“每小时航行15千米”,要求 “几小时可以到达”,
应该怎样计算? 解:设每小时航行x千米。
5x=20×6
x=120÷5
x=24
答:每小时应航行24千米。 解:设x小时可以到达。
15x=20×6
x=120÷15
x=8
答:8小时可以到达。试一试:同学们做操,每行站30人,正好站12行,
如果每行站36人,可以站多少行?解:设可以站x行。
36x=30×12
x=360÷36
x=10
答:可以站10行。
1、用比例解下面的应用题。电视机厂生产一批电视机,原计划每天生产
40台,30天完成, (1)实际24天就完成了生产任务,实际每天
生产多少台?(2)实际每天生产50台,实际几天完成
生产任务?(3)实际每天比计划多生产10台,
实际几天完成任务?
2、根据给出的算式,把应用题补充完整。(1)一本故事书,每天读18页,15天读完,
_______________________________?
30x=18×15(2)一批货物,如果每天运160吨,20天可以运完。
_______________________________________?
16x=160×20
2:怎样的两个量是成反比例的量?什么是反比例关系?用字母应如何表示?
1: 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用 来表示两种相关联的量,用字母 表示它们的比值(一定),正比例关系可以表示为:
2: 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用 来表示两种相关联的量,用字母 表示它们的积(一定),反比例关系可以表示为:
3:判断下面每题中两种量成正比例还是成反比例 (1) 单价一定,数量和总价
(2) 路程一定,速度和时间
(3) 工作时间一定,工作总量和工作效率
(4) 长方形的面积一定,长和宽 (成正比例)(成反比例)(成正比例)(成反比例) 在表1中相关联的量是( )和( ),( )随着( )变化,( )是一定的。因此,时间和路程成( )比例关系。二:一起来学习(1)例7:观察下面两个表格并回答问题:
表1 路程路程时间 速度正时间 问题:从表1中,你是怎样发现速度是一定的?又根据什么判断出路程和时间成正比例?
表2 在表2中相关联的量是( )和( ),( )随着( )变化,( )是一定的。因此,时间和速度成( )比例关系。速度时间路程时间速度反 问题:从表2中,你是怎样发现路程是一定的?又根据什么判断出时间和速度成反比例?关系是:当路程一定时,速度和时间成反比例。 当时间一定时,路程和速度成正比例。 当速度一定时,路程和时间成正比例。 问题: 路程,速度和时间这三种量之间有怎样的关系?当其中的一个量一定时,其它的两个量存在怎样的比例关系?(2)动脑想一下:(3)细心比一比:1 、都是两种相关联的量
2 、一种量变化,另一种量也随着变化 1 、“变化方向”相同,一种量扩大或缩小,另一种量也随着扩大或缩小。
2 、相对应的两个数的比值(商)是一定的。 1 、“变化方向”相反,一种量缩小或扩大,另一种量反而随着扩大或缩小。
2 、相对应的两个数的积是一定的。跟我学技巧:
正比反比两同胞,两点相同要记牢。首先必是关联量,一量随着另量变。比值一定成正比,乘积一定成反比。 三:巩固练习1:判断单价、数量和总价中一种量一定时,另外两种量成什么比例关系?为什么?
(1)单价一定,数量和总价 ( )
(2)总价一定,数量和单价 ( )
(3)数量一定,总价和单价 ( )成正比例 成正比例 成反比例 有三种!
面积一定时,长和宽成反比例。
长一定时,面积和宽成正比例。
宽一定时,面积和长成正比例。2:从长方形的长、宽和面积三种量中,你能找出几种比例关系?
3:已知x和y成正比例,试填下表并根据表中的数据列出两个比例式:
4:已知当 一定时, 和 成( )比例
当 一定时, 和 成( )比例
当 一定时, 和 成( )比例31652478:2=12:3 16:4=20:5正正反四:课堂小结 今天我们学习了那些知识?你学会了吗?五:活动探究1:正方形的面积和边长是否成比例?为什么?
2:圆的面积和半径是否成比例?为什么?
a
2、根据下列条件,列出等式。(1)用一批纸装订练习本,每本30页,可装订200本,
每本50页,可装订120本。(2)火车从甲地到乙地,每小时行驶30千米,
8小时到达。如果要6小时到达,每小时
必须行驶40千米。(3)读一本书,每天读20页,6天可以读完,
如果每天读5页,需要x天读完。30×1200=50×120 30×8=40×620×6=5x例题: -艘货轮每小时航行20千米,6小时可以到达
目的地。如果要5小时到达,每小时应航行多少千米? 如果“每小时航行15千米”,要求 “几小时可以到达”,
应该怎样计算? 解:设每小时航行x千米。
5x=20×6
x=120÷5
x=24
答:每小时应航行24千米。 解:设x小时可以到达。
15x=20×6
x=120÷15
x=8
答:8小时可以到达。试一试:同学们做操,每行站30人,正好站12行,
如果每行站36人,可以站多少行?解:设可以站x行。
36x=30×12
x=360÷36
x=10
答:可以站10行。
1、用比例解下面的应用题。电视机厂生产一批电视机,原计划每天生产
40台,30天完成, (1)实际24天就完成了生产任务,实际每天
生产多少台?(2)实际每天生产50台,实际几天完成
生产任务?(3)实际每天比计划多生产10台,
实际几天完成任务?
2、根据给出的算式,把应用题补充完整。(1)一本故事书,每天读18页,15天读完,
_______________________________?
30x=18×15(2)一批货物,如果每天运160吨,20天可以运完。
_______________________________________?
16x=160×20
