黑龙江省哈尔滨市松北区2017-2018学年(五四学制)六年级(下)期末数学试卷(解析版)
文档属性
| 名称 | 黑龙江省哈尔滨市松北区2017-2018学年(五四学制)六年级(下)期末数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-06 00:00:00 | ||
图片预览




文档简介
黑龙江省哈尔滨市松北区2017-2018学年(五四学制)六年级(下)期末数学试卷
一、选择题(每小题3分,共30分)
1.﹣(﹣)的相反数是( )
A.﹣ B. C.± D.﹣
2.下列计算正确的是( )
A.4a﹣9a=5a B.3(a+2b)=3a+6b
C.a+a=a2 D.3a+2b=5ab
3.如图是某一几何体从三个不同方向看到的图形,则这个几何体是( )
A.圆锥 B.三棱柱 C.三棱锥 D.圆柱
4.下列调查中,适宜采用全面调查方式的是( )
A.对某公园的全年游客流量情况调查
B.对松北区居民日平均用水量情况调查
C.对某中学在职教师身体的身体健康情况调查
D.对松花江流域水质的情况调查
5.如图AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
6.多项式a﹣(b﹣c)去括号的结果是( )
A.a﹣b﹣c B.a+b﹣c C.a+b+c D.a﹣b+c
7.如图,关于射线OA所指方向描述正确的是( )
A.东偏北26° B.北偏西64° C.西偏北64° D.南偏西64°
8.有理数a在数轴上的位置如图所示,下列结论正确的是( )
A.﹣2+a是负数 B.﹣2+a是正数 C.a﹣2是负数 D.a﹣2为0
9.下面四个整式中,不能表示图中阴影部分面积的是( )
A.x2+5x B.x(x+3)+6
C.3(x+2)+x2 D.(x+3)(x+2)﹣2x
10.下列说法中,正确的个数是( )
(1)在数轴上离原点越远的点所对应的数的绝对值越大
(2)若|a|=|b|,则a=b
(3)多项式﹣5x2﹣2x+1的一次项系数是﹣2
(4)角的两边越长,角越大
(5)若AP=BP,则P是线段AB的中点.
A.1 B.2 C.3 D.4
二、填空题:(每题3分,共30分)
11.2018年黑龙江省高考报考人数约为191000人,将191000用科学记数法表示应是 .
12.比较大小:﹣ (填“>”或“<”).
13.化简4x﹣3(x+1)= .
14.一个角比它的补角少40°,则这个角为 度.
15.已知14x5y2和2xm﹣1yn是同类项,则m+n= .
16.如图,OC是∠AOB的三等分线,且∠AOC=90°,则∠AOB= .
17.若代数式3a2﹣a=6,那么代数式8+2a﹣6a2的值为 .
18.某船顺水航行3小时,逆水航行2小时,已知轮船在静水中的速度为a千米/时,水流速度为b千米/时,轮船共航行 千米.
19.已知点N是线段AB的中点,点M是线段NB的三等分点,且MN=2cm,则线段AB= .
20.如图,把一个长方形纸片ABCD的一角折起来,折痕为BE,使∠EBM=∠MBC,若再沿BD对折长方形ABCD,点A落在点N处,且∠EBN=92.5°,则∠MBD= .
三、解答题(其中21、22题各7分,23、24题各8分,2527题各10分,共60分)
21.计算:
(1)(﹣﹣)÷
(2)2(a﹣2b)﹣3(2a﹣b)
22.先化简,再求值:(3x2y﹣2xy2)﹣2(2x2y﹣xy2),其中x=﹣1,y=2.
23.如图,已知四边形ABCD
(1)画直线AC.
(2)画射线BD,射线BD与直线AC相交于点O;
(3)延长线段BA与线段CD的延长线相交于点K;
(4)连接OK.
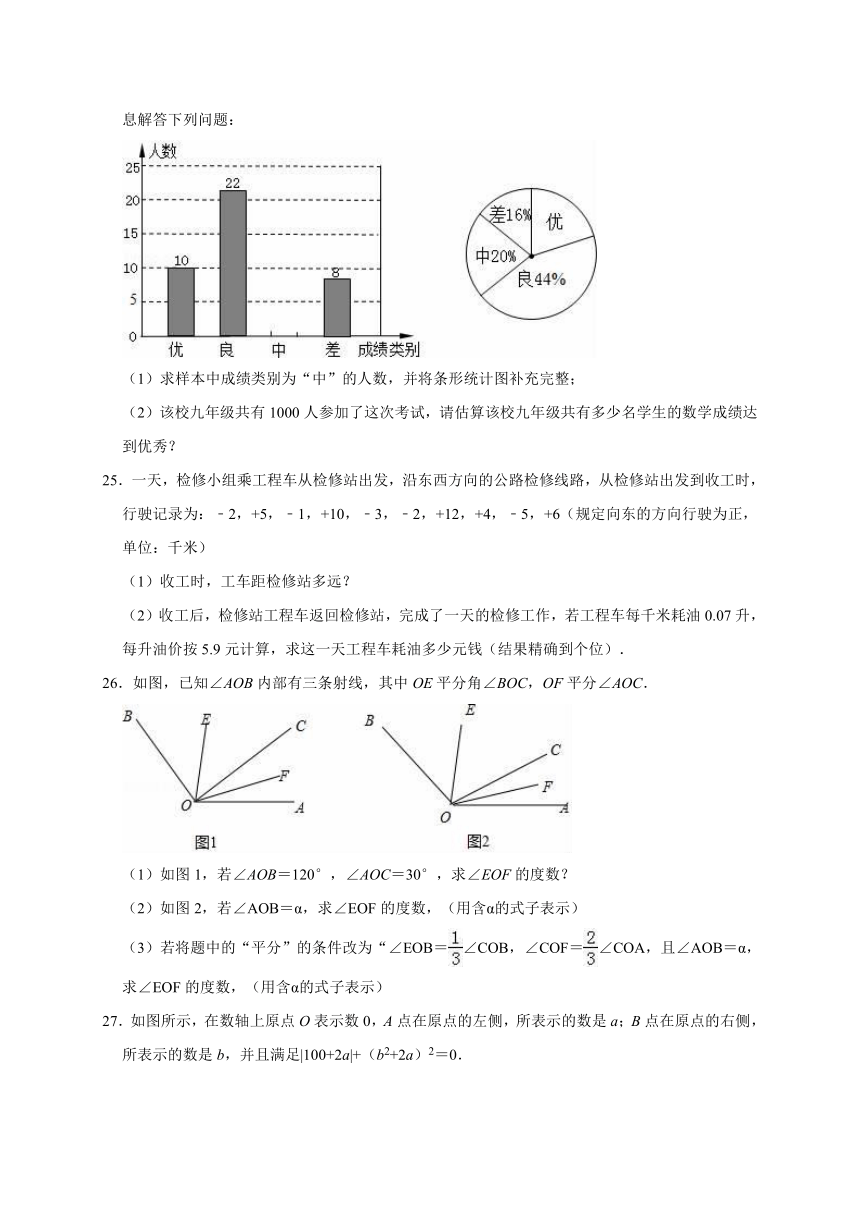
24.为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求样本中成绩类别为“中”的人数,并将条形统计图补充完整;
(2)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
25.一天,检修小组乘工程车从检修站出发,沿东西方向的公路检修线路,从检修站出发到收工时,行驶记录为:﹣2,+5,﹣1,+10,﹣3,﹣2,+12,+4,﹣5,+6(规定向东的方向行驶为正,单位:千米)
(1)收工时,工车距检修站多远?
(2)收工后,检修站工程车返回检修站,完成了一天的检修工作,若工程车每千米耗油0.07升,每升油价按5.9元计算,求这一天工程车耗油多少元钱(结果精确到个位).
26.如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.
(1)如图1,若∠AOB=120°,∠AOC=30°,求∠EOF的度数?
(2)如图2,若∠AOB=α,求∠EOF的度数,(用含α的式子表示)
(3)若将题中的“平分”的条件改为“∠EOB=∠COB,∠COF=∠COA,且∠AOB=α,求∠EOF的度数,(用含α的式子表示)
27.如图所示,在数轴上原点O表示数0,A点在原点的左侧,所表示的数是a;B点在原点的右侧,所表示的数是b,并且满足|100+2a|+(b2+2a)2=0.
(1)点A表示的数为 ,点B表示的数为 ;
(2)若点P从点A出发沿数轴向右运动,速度为每秒3个单位长度;点Q从点B出发沿数轴向左运动,速度为每秒1个单位长度.P、Q两点同时运动,并且在点C处相遇,试求点C所表示的数.
(3)在(2)的条件下,若点P运动到达B点后按原路原速立即返回,点Q继续按原速原方向运动,从P、Q在点C处相遇开始,再经过多少秒,P、Q两点的距离为12个单位长度.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.解:﹣(﹣)的相反数是﹣.
故选:A.
2.解:A、4a﹣9a=﹣5a,故原题计算错误;
B、3(a+2b)=3a+6b,故原题计算正确;
C、a+a=2a,故原题计算错误;
D、3a和2b不能合并,故原题计算错误;
故选:B.
3.解:∵主视图和左视图都是三角形,
∴此几何体为椎体,
∵俯视图是一个圆,
∴此几何体为圆锥.
故选:A.
4.解:A、对某公园的全年游客流量情况调查适合抽样调查;
B、对松北区居民日平均用水量情况调查适合抽样调查;
C、对某中学在职教师身体的身体健康情况调查适合全面调查;
D、对松花江流域水质的情况调查适合抽样调查;
故选:C.
5.解:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故选:C.
6.解:a﹣(b﹣c)=a﹣b+c.
故选:D.
7.解:根据方位角的概念,射线OA表示的方向是北偏西64°.
故选:B.
8.解:由数轴知a>0,且|a|>2,
则﹣a+2是正数、a﹣2是正数,
故选:B.
9.解:由图可得,
图中阴影部分的面积为:x2+3x+2×3=x2+3x+6,故选项A符合题意,
x(x+3)+2×3=x(x+3)+6,故选项B不符合题意,
3(x+2)+x2,故选项C不符合题意,
(x+3)(x+2)﹣2x,故选项D不符合题意,
故选:A.
10.解:(1)在数轴上离原点越远的点所对应的数的绝对值越大,此说法正确;
(2)若|a|=|b|,则a=b或a=﹣b,此说法错误;
(3)多项式﹣5x2﹣2x+1的一次项系数是﹣2,此说法正确;
(4)角的两边是射线,长度不能度量,此说法错误;
(5)若AP=BP且A、B、P在同一直线上,则P是线段AB的中点,此说法错误;
故选:B.
二、填空题:(每题3分,共30分)
11.解:191000=1.91×105,
故答案为:1.91×105.
12.解:∵|﹣|=,|﹣|=,
∴﹣>﹣,
故答案为:>
13.解:原式=4x﹣3x﹣3=x﹣3,
故答案为:x﹣3
14.解:设这个角为x,则这个角的补角为(180﹣x),那么
180°﹣x﹣40°=x,
解得x=70°.
答:这个角为70°.
故答案为:70.
15.解:因为14x5y2和2xm﹣1yn是同类项,
所以m﹣1=5,n=2,
解得:m=6,n=2,
所以m+n=2+6=8,
故答案为;8
16.解:∵OC是∠AOB的三等分线,
∴∠AOC=∠AOB,
∵∠AOC=90°,
∠AOB=135°,
故答案为135°.
17.解:∵3a2﹣a=6,
∴原式=8﹣2(3a2﹣a)=8﹣12=﹣4,
故答案为:﹣4
18.解:由题意得:顺水速度是:(a+b)千米/时,顺水路程为3(a+b)千米,
逆水速度是:(a﹣b)千米/时,逆水路程为2(a﹣b)千米,
轮船共航行路程:3(a+b)+2(a﹣b)=5a+b(千米),
故答案为:(5a+b).
19.解:∵点M是线段NB的三等分点,
∴MN=BN或MN=BN.
∵MN=2cm,
∴BN=6cm或3cm.
又∵点N是线段AB的中点,
∴AB=2BN,
∴AB=12cm或6cm.
故答案为:12cm或6cm.
20.解:∵将△ABE折叠到△BEM位置
∴∠ABE=∠EBM
∵∠EBM=∠MBC
∴∠ABM=∠MBC
∵∠ABM+∠MBC=90°
∴∠ABM=45°,∠EBM=22.5°
设∠MBD=x°,则∠ABD=(45+x)°
∵将△ABD折叠到△BDN位置
∴∠ABD=∠DBN=(45+x)°
∵∠EBN=92.5°
∴22.5+x+45+x=92.5
∴x=12.5°
∴∠MBD=12.5°
故答案为12.5°
三、解答题(其中21、22题各7分,23、24题各8分,2527题各10分,共60分)
21.解:(1)原式=(﹣﹣)×24
=×24﹣×24﹣×24
=32﹣9﹣2
=21;
(2)原式=2a﹣4b﹣6a+3b
=﹣4a﹣b.
22.解:当x=﹣1,y=2时,
原式=3x2y﹣2xy2﹣4x2y+2xy2
=﹣x2y
=﹣2
23.解:(1)直线AC如图所示;
(2)射线BD,射线BD与直线AC相较于点O如图所示;
(3)延长线段BA与线段CD的延长线相较于点K如图所示;
(4)连接OK如图所示;
24.解:(1)样本容量为8÷16%=50,
所以成绩类别为“中”的人数等于50×20%=10(人);
如图;
(2)1000××100%=200,
所以估计该校九年级共有200名学生的数学成绩可以达到优秀.
25.(1)(﹣2)+(+5)+(﹣1)+(+10)+(﹣3)+(﹣2)+(+12)+(+4)+(﹣5)+(+6)=24千米
答:收工时,工程车距检修站24千米
(2)2+5+1+10+3+2+12+4+5+6+24=74(千米),
74×0.07×5.9≈31(元).
答:这一天工程车耗油31元.
26.解:(1)∵OF平分∠AOC,
∴∠COF=∠AOC=×30°=15°,
∵∠BOC=∠AOB﹣∠AOC=120°﹣30°=90°,OE平分∠BOC,
∴∠EOC=∠BOC=45°,
∴∠EOF=∠COF+∠EOC=60°;
(2)∵OF平分∠AOC,
∴∠COF=∠AOC,
同理,∠EOC=∠BOC,
∴∠EOF=∠COF+∠EOC
=∠AOC+∠BOC
=(∠AOC+∠BOC)
=∠AOB
=α;
(3)∵∠EOB=∠COB,
∴∠EOC=∠COB,
∴∠EOF=∠EOC+∠COF
=∠COB+∠COA
=∠BOC+∠AOC
=∠AOB
=α.
27.解:(1)∵|100+2a|+(b2+2a)2=0,
∴a=﹣50,b=±10(负值舍去)
∴点A表示的数为﹣50,点B表示的数为10;
故答案为:﹣50,10;
(2)设P、Q两点同时运动t秒相遇
3t+t=60,
解得t=15,
此时C所表示的数为﹣50+3×15=﹣5.
答:C点表示的数为﹣5;
(3)设再经过a秒钟,P、Q两点的距离为12个单位长度
①a+3a=12,解得a=3;
②a+15﹣(3a﹣15)=12,解得a=9;
③3a﹣15﹣(a+15)=12,解得a=21.
故从P、Q在点C处相遇开始,再经过3秒或9秒或21秒,P、Q两点的距离为12个单位长度.
一、选择题(每小题3分,共30分)
1.﹣(﹣)的相反数是( )
A.﹣ B. C.± D.﹣
2.下列计算正确的是( )
A.4a﹣9a=5a B.3(a+2b)=3a+6b
C.a+a=a2 D.3a+2b=5ab
3.如图是某一几何体从三个不同方向看到的图形,则这个几何体是( )
A.圆锥 B.三棱柱 C.三棱锥 D.圆柱
4.下列调查中,适宜采用全面调查方式的是( )
A.对某公园的全年游客流量情况调查
B.对松北区居民日平均用水量情况调查
C.对某中学在职教师身体的身体健康情况调查
D.对松花江流域水质的情况调查
5.如图AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.无法确定
6.多项式a﹣(b﹣c)去括号的结果是( )
A.a﹣b﹣c B.a+b﹣c C.a+b+c D.a﹣b+c
7.如图,关于射线OA所指方向描述正确的是( )
A.东偏北26° B.北偏西64° C.西偏北64° D.南偏西64°
8.有理数a在数轴上的位置如图所示,下列结论正确的是( )
A.﹣2+a是负数 B.﹣2+a是正数 C.a﹣2是负数 D.a﹣2为0
9.下面四个整式中,不能表示图中阴影部分面积的是( )
A.x2+5x B.x(x+3)+6
C.3(x+2)+x2 D.(x+3)(x+2)﹣2x
10.下列说法中,正确的个数是( )
(1)在数轴上离原点越远的点所对应的数的绝对值越大
(2)若|a|=|b|,则a=b
(3)多项式﹣5x2﹣2x+1的一次项系数是﹣2
(4)角的两边越长,角越大
(5)若AP=BP,则P是线段AB的中点.
A.1 B.2 C.3 D.4
二、填空题:(每题3分,共30分)
11.2018年黑龙江省高考报考人数约为191000人,将191000用科学记数法表示应是 .
12.比较大小:﹣ (填“>”或“<”).
13.化简4x﹣3(x+1)= .
14.一个角比它的补角少40°,则这个角为 度.
15.已知14x5y2和2xm﹣1yn是同类项,则m+n= .
16.如图,OC是∠AOB的三等分线,且∠AOC=90°,则∠AOB= .
17.若代数式3a2﹣a=6,那么代数式8+2a﹣6a2的值为 .
18.某船顺水航行3小时,逆水航行2小时,已知轮船在静水中的速度为a千米/时,水流速度为b千米/时,轮船共航行 千米.
19.已知点N是线段AB的中点,点M是线段NB的三等分点,且MN=2cm,则线段AB= .
20.如图,把一个长方形纸片ABCD的一角折起来,折痕为BE,使∠EBM=∠MBC,若再沿BD对折长方形ABCD,点A落在点N处,且∠EBN=92.5°,则∠MBD= .
三、解答题(其中21、22题各7分,23、24题各8分,2527题各10分,共60分)
21.计算:
(1)(﹣﹣)÷
(2)2(a﹣2b)﹣3(2a﹣b)
22.先化简,再求值:(3x2y﹣2xy2)﹣2(2x2y﹣xy2),其中x=﹣1,y=2.
23.如图,已知四边形ABCD
(1)画直线AC.
(2)画射线BD,射线BD与直线AC相交于点O;
(3)延长线段BA与线段CD的延长线相交于点K;
(4)连接OK.
24.为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求样本中成绩类别为“中”的人数,并将条形统计图补充完整;
(2)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
25.一天,检修小组乘工程车从检修站出发,沿东西方向的公路检修线路,从检修站出发到收工时,行驶记录为:﹣2,+5,﹣1,+10,﹣3,﹣2,+12,+4,﹣5,+6(规定向东的方向行驶为正,单位:千米)
(1)收工时,工车距检修站多远?
(2)收工后,检修站工程车返回检修站,完成了一天的检修工作,若工程车每千米耗油0.07升,每升油价按5.9元计算,求这一天工程车耗油多少元钱(结果精确到个位).
26.如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.
(1)如图1,若∠AOB=120°,∠AOC=30°,求∠EOF的度数?
(2)如图2,若∠AOB=α,求∠EOF的度数,(用含α的式子表示)
(3)若将题中的“平分”的条件改为“∠EOB=∠COB,∠COF=∠COA,且∠AOB=α,求∠EOF的度数,(用含α的式子表示)
27.如图所示,在数轴上原点O表示数0,A点在原点的左侧,所表示的数是a;B点在原点的右侧,所表示的数是b,并且满足|100+2a|+(b2+2a)2=0.
(1)点A表示的数为 ,点B表示的数为 ;
(2)若点P从点A出发沿数轴向右运动,速度为每秒3个单位长度;点Q从点B出发沿数轴向左运动,速度为每秒1个单位长度.P、Q两点同时运动,并且在点C处相遇,试求点C所表示的数.
(3)在(2)的条件下,若点P运动到达B点后按原路原速立即返回,点Q继续按原速原方向运动,从P、Q在点C处相遇开始,再经过多少秒,P、Q两点的距离为12个单位长度.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.解:﹣(﹣)的相反数是﹣.
故选:A.
2.解:A、4a﹣9a=﹣5a,故原题计算错误;
B、3(a+2b)=3a+6b,故原题计算正确;
C、a+a=2a,故原题计算错误;
D、3a和2b不能合并,故原题计算错误;
故选:B.
3.解:∵主视图和左视图都是三角形,
∴此几何体为椎体,
∵俯视图是一个圆,
∴此几何体为圆锥.
故选:A.
4.解:A、对某公园的全年游客流量情况调查适合抽样调查;
B、对松北区居民日平均用水量情况调查适合抽样调查;
C、对某中学在职教师身体的身体健康情况调查适合全面调查;
D、对松花江流域水质的情况调查适合抽样调查;
故选:C.
5.解:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故选:C.
6.解:a﹣(b﹣c)=a﹣b+c.
故选:D.
7.解:根据方位角的概念,射线OA表示的方向是北偏西64°.
故选:B.
8.解:由数轴知a>0,且|a|>2,
则﹣a+2是正数、a﹣2是正数,
故选:B.
9.解:由图可得,
图中阴影部分的面积为:x2+3x+2×3=x2+3x+6,故选项A符合题意,
x(x+3)+2×3=x(x+3)+6,故选项B不符合题意,
3(x+2)+x2,故选项C不符合题意,
(x+3)(x+2)﹣2x,故选项D不符合题意,
故选:A.
10.解:(1)在数轴上离原点越远的点所对应的数的绝对值越大,此说法正确;
(2)若|a|=|b|,则a=b或a=﹣b,此说法错误;
(3)多项式﹣5x2﹣2x+1的一次项系数是﹣2,此说法正确;
(4)角的两边是射线,长度不能度量,此说法错误;
(5)若AP=BP且A、B、P在同一直线上,则P是线段AB的中点,此说法错误;
故选:B.
二、填空题:(每题3分,共30分)
11.解:191000=1.91×105,
故答案为:1.91×105.
12.解:∵|﹣|=,|﹣|=,
∴﹣>﹣,
故答案为:>
13.解:原式=4x﹣3x﹣3=x﹣3,
故答案为:x﹣3
14.解:设这个角为x,则这个角的补角为(180﹣x),那么
180°﹣x﹣40°=x,
解得x=70°.
答:这个角为70°.
故答案为:70.
15.解:因为14x5y2和2xm﹣1yn是同类项,
所以m﹣1=5,n=2,
解得:m=6,n=2,
所以m+n=2+6=8,
故答案为;8
16.解:∵OC是∠AOB的三等分线,
∴∠AOC=∠AOB,
∵∠AOC=90°,
∠AOB=135°,
故答案为135°.
17.解:∵3a2﹣a=6,
∴原式=8﹣2(3a2﹣a)=8﹣12=﹣4,
故答案为:﹣4
18.解:由题意得:顺水速度是:(a+b)千米/时,顺水路程为3(a+b)千米,
逆水速度是:(a﹣b)千米/时,逆水路程为2(a﹣b)千米,
轮船共航行路程:3(a+b)+2(a﹣b)=5a+b(千米),
故答案为:(5a+b).
19.解:∵点M是线段NB的三等分点,
∴MN=BN或MN=BN.
∵MN=2cm,
∴BN=6cm或3cm.
又∵点N是线段AB的中点,
∴AB=2BN,
∴AB=12cm或6cm.
故答案为:12cm或6cm.
20.解:∵将△ABE折叠到△BEM位置
∴∠ABE=∠EBM
∵∠EBM=∠MBC
∴∠ABM=∠MBC
∵∠ABM+∠MBC=90°
∴∠ABM=45°,∠EBM=22.5°
设∠MBD=x°,则∠ABD=(45+x)°
∵将△ABD折叠到△BDN位置
∴∠ABD=∠DBN=(45+x)°
∵∠EBN=92.5°
∴22.5+x+45+x=92.5
∴x=12.5°
∴∠MBD=12.5°
故答案为12.5°
三、解答题(其中21、22题各7分,23、24题各8分,2527题各10分,共60分)
21.解:(1)原式=(﹣﹣)×24
=×24﹣×24﹣×24
=32﹣9﹣2
=21;
(2)原式=2a﹣4b﹣6a+3b
=﹣4a﹣b.
22.解:当x=﹣1,y=2时,
原式=3x2y﹣2xy2﹣4x2y+2xy2
=﹣x2y
=﹣2
23.解:(1)直线AC如图所示;
(2)射线BD,射线BD与直线AC相较于点O如图所示;
(3)延长线段BA与线段CD的延长线相较于点K如图所示;
(4)连接OK如图所示;
24.解:(1)样本容量为8÷16%=50,
所以成绩类别为“中”的人数等于50×20%=10(人);
如图;
(2)1000××100%=200,
所以估计该校九年级共有200名学生的数学成绩可以达到优秀.
25.(1)(﹣2)+(+5)+(﹣1)+(+10)+(﹣3)+(﹣2)+(+12)+(+4)+(﹣5)+(+6)=24千米
答:收工时,工程车距检修站24千米
(2)2+5+1+10+3+2+12+4+5+6+24=74(千米),
74×0.07×5.9≈31(元).
答:这一天工程车耗油31元.
26.解:(1)∵OF平分∠AOC,
∴∠COF=∠AOC=×30°=15°,
∵∠BOC=∠AOB﹣∠AOC=120°﹣30°=90°,OE平分∠BOC,
∴∠EOC=∠BOC=45°,
∴∠EOF=∠COF+∠EOC=60°;
(2)∵OF平分∠AOC,
∴∠COF=∠AOC,
同理,∠EOC=∠BOC,
∴∠EOF=∠COF+∠EOC
=∠AOC+∠BOC
=(∠AOC+∠BOC)
=∠AOB
=α;
(3)∵∠EOB=∠COB,
∴∠EOC=∠COB,
∴∠EOF=∠EOC+∠COF
=∠COB+∠COA
=∠BOC+∠AOC
=∠AOB
=α.
27.解:(1)∵|100+2a|+(b2+2a)2=0,
∴a=﹣50,b=±10(负值舍去)
∴点A表示的数为﹣50,点B表示的数为10;
故答案为:﹣50,10;
(2)设P、Q两点同时运动t秒相遇
3t+t=60,
解得t=15,
此时C所表示的数为﹣50+3×15=﹣5.
答:C点表示的数为﹣5;
(3)设再经过a秒钟,P、Q两点的距离为12个单位长度
①a+3a=12,解得a=3;
②a+15﹣(3a﹣15)=12,解得a=9;
③3a﹣15﹣(a+15)=12,解得a=21.
故从P、Q在点C处相遇开始,再经过3秒或9秒或21秒,P、Q两点的距离为12个单位长度.
同课章节目录
