黑龙江省哈尔滨市香坊区2017-2018学年(五四学制)六年级(下)期末数学试卷解析版
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区2017-2018学年(五四学制)六年级(下)期末数学试卷解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-06 00:00:00 | ||
图片预览




文档简介
黑龙江省哈尔滨市香坊区2017-2018学年(五四学制)六年级(下)期末数学试卷
一、选择题(每小题3分,共计30分)
1.气温由﹣2℃上升3℃后是( )℃.
A.1 B.3 C.5 D.﹣5
2.下列各式运算正确的是( )
A.2(a﹣1)=2a﹣1 B.a2b﹣ab2=0
C.2a3﹣3a3=a3 D.a2+a2=2a2
3.下列调查中,适宜采用全面调查方式的是( )
A.对我国中学生体重的调查
B.对我国市场上某一品牌食品质量的调查
C.了解一批电池的使用寿命
D.了解某班学生的身高情况
4.点C在线段AB上,下列条件不能确定点C为线段AB中点的是( )
A.AB=2AC B.AC=2BC C.AC=BC D.BC=AB
5.如图,点A位于点O的( )
A.南偏东35°方向上 B.北偏西65°方向上
C.南偏东65°方向上 D.南偏西65°方向上
6.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
A.的 B.中 C.国 D.梦
7.式子m+5,﹣,2x,,﹣中,单项式有( )
A.1个 B.2个 C.3个 D.4个
8.有理数a、b在数轴上对应的位置如图所示,则下列关系正确的是( )
A.﹣a<﹣b B.a<﹣b C.b<﹣a D.﹣b<a
9.代数式m3+n的值为5,则代数式﹣m3﹣n+2的值为( )
A.﹣3 B.3 C.﹣7 D.7
10.下列说法:①两点之间,线段最短;②正数和负数统称为有理数;③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式;④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成7组;⑤一个锐角的补角与这个角的余角的差是直角,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共计30分)
11.四川航空一航班在近万米高空遭遇驾驶舱挡风玻璃破裂脱落,随后安全备降成都双流国际机场.航班事发时距离地面32000英尺,请用科学记数法表示32000为 .
12.计算:18°26′+20°46′=
13.多项式5x+2y与多项式6x﹣3y的差是
14.在一个样本中,50个数据分别落在5个小组内,第一、二、三、五组数据的频数分别为2、8、15、5,则第四小组数据的频数为
15.写出一个x的值,使|x﹣1|=﹣x+1成立,你写出的x的值是
16.多项式﹣2m3+3m2﹣m的各项系数之积为
17.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为 .
18.如图,以图中的A、B、C、D为端点的线段共有 条.
19.观察下列图形:它们是按一定规律排列的,依照此规律,第n个图形共有 个点.
20.已知点B、C为线段AD上的两点,AB=BC=CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.(7分)计算:
(1)()
(2)﹣22×()2
22.(7分)先化简,再求值: x﹣2(x﹣)+(﹣),其中x=﹣1,y=
23.(8分)按要求解答:
(1)如图,平面内有四点A、B、C、D,画出符合下列所有要求的图形.
①画直线AB;
②画射线CD;
③连接线段AD、BC相交于点P;
④延长BD至Q,使DQ=BD.
(2)已知一个角的补角比这个角的余角的3倍少50°,求这个角是多少度?
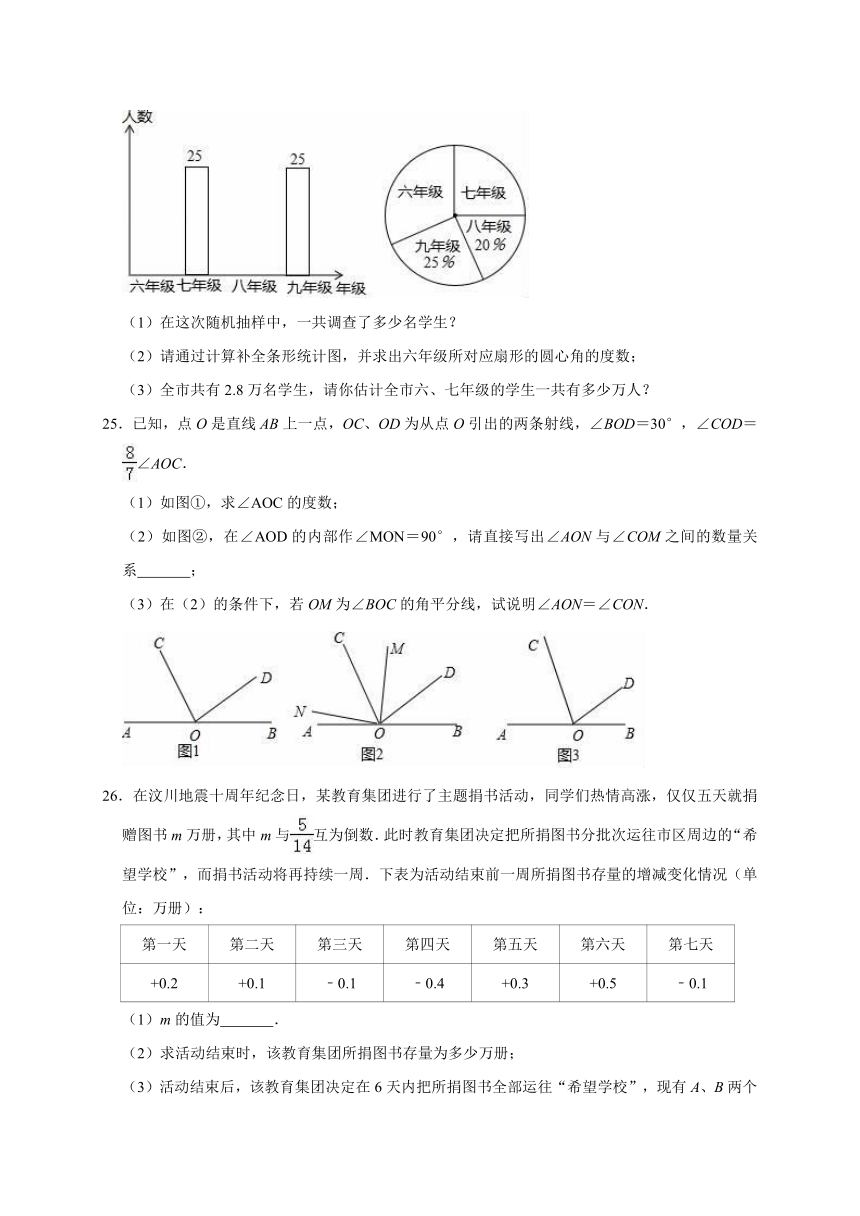
24.(8分)哈市要对2.8万名初中生“学段人数分布情况”进行调查,采取随机抽样的方法从四个学年中抽取了若干名学生,并将调查结果绘制成了如下两幅不完整的条形统计图和扇形统计图,请根据图中提供的信息解答下列问题:
(1)在这次随机抽样中,一共调查了多少名学生?
(2)请通过计算补全条形统计图,并求出六年级所对应扇形的圆心角的度数;
(3)全市共有2.8万名学生,请你估计全市六、七年级的学生一共有多少万人?
25.已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
26.在汶川地震十周年纪念日,某教育集团进行了主题捐书活动,同学们热情高涨,仅仅五天就捐赠图书m万册,其中m与互为倒数.此时教育集团决定把所捐图书分批次运往市区周边的“希望学校”,而捐书活动将再持续一周.下表为活动结束前一周所捐图书存量的增减变化情况(单位:万册):
第一天 第二天 第三天 第四天 第五天 第六天 第七天
+0.2 +0.1 ﹣0.1 ﹣0.4 +0.3 +0.5 ﹣0.1
(1)m的值为 .
(2)求活动结束时,该教育集团所捐图书存量为多少万册;
(3)活动结束后,该教育集团决定在6天内把所捐图书全部运往“希望学校”,现有A、B两个运输公司,B运输公司每天的运输数量是A运输公司的1.5倍,学校首先聘请A运输公司进行运输,工作两天后,由于某些原因,A运输公司每天运输的数量比原来降低了25%,学校决定又聘请B运输公司加入,与A运输公司共同运输,恰好按时完成任务,求A运输公司每天运输多少万册图书?
27.如图,O为原点,数轴上两点A、B所对应的数分别为m、n,且m、n满足关于x、y的整式x41+myn+60与2xy3m之和是单项式,动点P以每秒4个单位长度的速度从点A向终点B运动.
(1)求m、n的值;
(2)当PB﹣(PA+PO)=10时,求点P的运动时间t的值;
(3)当点P开始运动时,点Q也同时以每秒2个单位长度的速度从点B向终点A运动,若PQ=AB,求AP的长.
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.解:由题意,得
﹣2+3=+(3﹣2)=1,
故选:A.
2.解:A、2(a﹣1)=2a﹣2,故此选项错误;
B、a2b﹣ab2,无法合并,故此选项错误;
C、2a3﹣3a3=﹣a3,故此选项错误;
D、a2+a2=2a2,正确.
故选:D.
3.解:对我国中学生体重的调查适宜采用抽样调查方式;
对我国市场上某一品牌食品质量的调查适宜采用抽样调查方式;
了解一批电池的使用寿命适宜采用抽样调查方式;
了解某班学生的身高情况适宜采用全面调查方式;
故选:D.
4.解:A:若点C在线段AB上,AB=2AC,则点C为线段AB的中点;
B:若点C在线段AB上,AC=2BC,则点C不是线段AB的中点;
C:若点C在线段AB上,AC=BC,则点C为线段AB的中点;
D:若点C在线段AB上,BC=AB,则点C为线段AB的中点..
故选:B.
5.解:由图可得,点A位于点O的北偏西65°的方向上.
故选:B.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”字一面的相对面上的字是“梦”.
故选:D.
7.解:式子﹣,2x,是单项式,共3个,
故选:C.
8.解:观察数轴,可知:﹣1<a<0,b>1,
∴﹣b<﹣1<a<0<﹣a<1<b.
故选:D.
9.解:∵代数式m3+n的值为5,
∴m3+n=5
∴﹣m3﹣n+2=﹣(m3+n)+2
=﹣5+2=﹣3
故选:A.
10.解:①两点之间,线段最短,此结论正确;
②正有理数、负有理数和0统称为有理数,此结论错误;
③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式,此结论正确;
④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成8组,此结论错误;
⑤一个锐角的补角与这个角的余角的差是直角,此结论正确;
故选:B.
二、填空题(每小题3分,共计30分)
11.解:用科学记数法表示32000为3.2×104.
故答案为:3.2×104.
12.解:18°26′+20°46′=38°72′=39°12′.
故答案为:39°12′.
13.解:根据题意得:(5x+2y)﹣(6x﹣3y)=5x+2y﹣6x+3y=﹣x+5y,
故答案为:﹣x+5y
14.解:由题意知:第四小组的频数=50﹣(2+8+15+5)=20,
故答案为:20
15.解:∵|x﹣1|=﹣x+1且|x﹣1|≥0,
∴﹣x+1≥0,
∴x≤1,
故答案为:0(答案不唯一)
16.解:多项式﹣2m3+3m2﹣m的各项系数之积为:
﹣2×3×(﹣)=3.
故答案为:3.
17.解:根据题意得:
∠AOC+∠DOB
=∠AOB+∠BOC+∠DOB
=∠AOB+∠COD
=90°+90°
=180°,
故答案为:180°.
18.解:图中的线段有:
线段AB,线段AC,线段AD,线段BC,线段BD,线段CD,共6条.
故答案为:6.
19.解:∵第1个图形中点的个数8=2×1+6,
第2个图形中点的个数10=2×2+6,
第3个图形中点的个数12=2×3+6,
第4个图形中点的个数14=2×4+6,
……
∴第n个图形中点的个数为2n+6,
故答案为:2n+6.
20.解:设AB=x,则BC=2x,CD=3x,CE=DE=CD=x,
∵BE=BC+CE=2x+x=14,
∴x=4.
∵点F为线段AD的三等分点,
∴AF=AD=2x或DF=AD=2x.
当AF=2x时,如图1所示,EF=AB+BC+CE﹣AF=x=10;
当DF=2x时,如图2所示,EF=DF﹣DE==2.
综上,线段EF的长为2或10.
故答案为:2或10.
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.解:(1)原式=(﹣+﹣)×24=﹣16+12﹣15=﹣19;
(2)原式=﹣4××=﹣.
22.解:原式=x﹣2x+y2﹣x+y2
=﹣3x+y2
当x=﹣1,y=时,
原式=﹣3×(﹣1)+
=
23.解:(1)如图所示:
(2)解:设这个角是x度,则
180﹣x=3(90﹣x)﹣50,
解得:x=20,
答:这个角是20度.
24.解:(1)本次调查的学生人数为25÷25%=100(名);
(2)八年级的人数为100×20%=20人,则六年级的人数为100﹣(25+20+25)=30,
补全图形如下:
六年级所对应扇形的圆心角的度数为360°×=108°;
(3)估计全市六、七年级的学生一共有2.8×=1.54(万人).
25.解:(1)由题意可知:∠AOB=180°,∠BOD=30°,
∠AOD=∠AOB﹣∠BOD=150°,
∵∠AOD=∠AOC+∠COD,∠COD=∠AOC,
∴∠AOC+∠AOC=150°,
∴∠AOC=70°;
(2)由图可见:∠AON+20°=∠COM,
故:答案为:∠AON+20°=∠COM;
(3)证明:∵∠AOC=70°,∠AOB=180°,
∴∠BOC=∠AOB﹣∠AOC=110°,
∵OM是∠BOC的角平分线
∴∠COM=∠BOC=55°,
∵∠MON=90°,
∴∠CON=∠MON﹣∠COM=35°,
∵∠AOC=70°,
∴∠AON=∠AOC﹣∠CON=35°,
∴∠AON=∠CON.
26.解:(1)∵m与互为倒数,
∴m==2.8.
故答案为:2.8;
(2)2.8+0.2+0.1﹣0.1﹣0.4+0.3+0.5﹣0.1=3.3(万册).
答:活动结束时,该教育集团所捐图书存量为3.3万册;
(3)设A运输公司每天运输x万册图书,则B运输公司每天运输1.5x万册图书,
根据题意得:2x+(6﹣2)[(1﹣25%)x+1.5x]=3.3,
解得:x=0.3.
答:A运输公司每天运输0.3万册图书.
27.解:(1)∵m、n满足关于x、y的整式x41+myn+60与2xy3m之和是单项式,
∴41+m=1,n+60=3n,
解得:m=﹣40,n=30.
(2)∵点A、B所对应的数分别为﹣40和30,
∴AB=70,AO=40,BO=30.
当点P在O的左侧时,PA+PO=AO=40,PB=AB﹣AP=70﹣4t.
∵PB﹣(PA+PO)=10,
∴70﹣4t﹣40=10,
∴t=5;
当点P在O的右侧时,∵PB<PA,
∴PB﹣(PA+PO)<0,不合题意,舍去.
(3)运动时间为t秒时,点P表示的数为4t﹣40,点Q表示的数为30﹣2t,
∵PQ=AB,
∴|30﹣2t﹣(4t﹣40)|=×70,
解得:t=或t=.
当t=时,AP=4t=;
当t=时,AP=4t=70.
答:若PQ=AB,则AP的长为或70.
一、选择题(每小题3分,共计30分)
1.气温由﹣2℃上升3℃后是( )℃.
A.1 B.3 C.5 D.﹣5
2.下列各式运算正确的是( )
A.2(a﹣1)=2a﹣1 B.a2b﹣ab2=0
C.2a3﹣3a3=a3 D.a2+a2=2a2
3.下列调查中,适宜采用全面调查方式的是( )
A.对我国中学生体重的调查
B.对我国市场上某一品牌食品质量的调查
C.了解一批电池的使用寿命
D.了解某班学生的身高情况
4.点C在线段AB上,下列条件不能确定点C为线段AB中点的是( )
A.AB=2AC B.AC=2BC C.AC=BC D.BC=AB
5.如图,点A位于点O的( )
A.南偏东35°方向上 B.北偏西65°方向上
C.南偏东65°方向上 D.南偏西65°方向上
6.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
A.的 B.中 C.国 D.梦
7.式子m+5,﹣,2x,,﹣中,单项式有( )
A.1个 B.2个 C.3个 D.4个
8.有理数a、b在数轴上对应的位置如图所示,则下列关系正确的是( )
A.﹣a<﹣b B.a<﹣b C.b<﹣a D.﹣b<a
9.代数式m3+n的值为5,则代数式﹣m3﹣n+2的值为( )
A.﹣3 B.3 C.﹣7 D.7
10.下列说法:①两点之间,线段最短;②正数和负数统称为有理数;③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式;④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成7组;⑤一个锐角的补角与这个角的余角的差是直角,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每小题3分,共计30分)
11.四川航空一航班在近万米高空遭遇驾驶舱挡风玻璃破裂脱落,随后安全备降成都双流国际机场.航班事发时距离地面32000英尺,请用科学记数法表示32000为 .
12.计算:18°26′+20°46′=
13.多项式5x+2y与多项式6x﹣3y的差是
14.在一个样本中,50个数据分别落在5个小组内,第一、二、三、五组数据的频数分别为2、8、15、5,则第四小组数据的频数为
15.写出一个x的值,使|x﹣1|=﹣x+1成立,你写出的x的值是
16.多项式﹣2m3+3m2﹣m的各项系数之积为
17.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为 .
18.如图,以图中的A、B、C、D为端点的线段共有 条.
19.观察下列图形:它们是按一定规律排列的,依照此规律,第n个图形共有 个点.
20.已知点B、C为线段AD上的两点,AB=BC=CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.(7分)计算:
(1)()
(2)﹣22×()2
22.(7分)先化简,再求值: x﹣2(x﹣)+(﹣),其中x=﹣1,y=
23.(8分)按要求解答:
(1)如图,平面内有四点A、B、C、D,画出符合下列所有要求的图形.
①画直线AB;
②画射线CD;
③连接线段AD、BC相交于点P;
④延长BD至Q,使DQ=BD.
(2)已知一个角的补角比这个角的余角的3倍少50°,求这个角是多少度?
24.(8分)哈市要对2.8万名初中生“学段人数分布情况”进行调查,采取随机抽样的方法从四个学年中抽取了若干名学生,并将调查结果绘制成了如下两幅不完整的条形统计图和扇形统计图,请根据图中提供的信息解答下列问题:
(1)在这次随机抽样中,一共调查了多少名学生?
(2)请通过计算补全条形统计图,并求出六年级所对应扇形的圆心角的度数;
(3)全市共有2.8万名学生,请你估计全市六、七年级的学生一共有多少万人?
25.已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.
26.在汶川地震十周年纪念日,某教育集团进行了主题捐书活动,同学们热情高涨,仅仅五天就捐赠图书m万册,其中m与互为倒数.此时教育集团决定把所捐图书分批次运往市区周边的“希望学校”,而捐书活动将再持续一周.下表为活动结束前一周所捐图书存量的增减变化情况(单位:万册):
第一天 第二天 第三天 第四天 第五天 第六天 第七天
+0.2 +0.1 ﹣0.1 ﹣0.4 +0.3 +0.5 ﹣0.1
(1)m的值为 .
(2)求活动结束时,该教育集团所捐图书存量为多少万册;
(3)活动结束后,该教育集团决定在6天内把所捐图书全部运往“希望学校”,现有A、B两个运输公司,B运输公司每天的运输数量是A运输公司的1.5倍,学校首先聘请A运输公司进行运输,工作两天后,由于某些原因,A运输公司每天运输的数量比原来降低了25%,学校决定又聘请B运输公司加入,与A运输公司共同运输,恰好按时完成任务,求A运输公司每天运输多少万册图书?
27.如图,O为原点,数轴上两点A、B所对应的数分别为m、n,且m、n满足关于x、y的整式x41+myn+60与2xy3m之和是单项式,动点P以每秒4个单位长度的速度从点A向终点B运动.
(1)求m、n的值;
(2)当PB﹣(PA+PO)=10时,求点P的运动时间t的值;
(3)当点P开始运动时,点Q也同时以每秒2个单位长度的速度从点B向终点A运动,若PQ=AB,求AP的长.
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.解:由题意,得
﹣2+3=+(3﹣2)=1,
故选:A.
2.解:A、2(a﹣1)=2a﹣2,故此选项错误;
B、a2b﹣ab2,无法合并,故此选项错误;
C、2a3﹣3a3=﹣a3,故此选项错误;
D、a2+a2=2a2,正确.
故选:D.
3.解:对我国中学生体重的调查适宜采用抽样调查方式;
对我国市场上某一品牌食品质量的调查适宜采用抽样调查方式;
了解一批电池的使用寿命适宜采用抽样调查方式;
了解某班学生的身高情况适宜采用全面调查方式;
故选:D.
4.解:A:若点C在线段AB上,AB=2AC,则点C为线段AB的中点;
B:若点C在线段AB上,AC=2BC,则点C不是线段AB的中点;
C:若点C在线段AB上,AC=BC,则点C为线段AB的中点;
D:若点C在线段AB上,BC=AB,则点C为线段AB的中点..
故选:B.
5.解:由图可得,点A位于点O的北偏西65°的方向上.
故选:B.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”字一面的相对面上的字是“梦”.
故选:D.
7.解:式子﹣,2x,是单项式,共3个,
故选:C.
8.解:观察数轴,可知:﹣1<a<0,b>1,
∴﹣b<﹣1<a<0<﹣a<1<b.
故选:D.
9.解:∵代数式m3+n的值为5,
∴m3+n=5
∴﹣m3﹣n+2=﹣(m3+n)+2
=﹣5+2=﹣3
故选:A.
10.解:①两点之间,线段最短,此结论正确;
②正有理数、负有理数和0统称为有理数,此结论错误;
③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式,此结论正确;
④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成8组,此结论错误;
⑤一个锐角的补角与这个角的余角的差是直角,此结论正确;
故选:B.
二、填空题(每小题3分,共计30分)
11.解:用科学记数法表示32000为3.2×104.
故答案为:3.2×104.
12.解:18°26′+20°46′=38°72′=39°12′.
故答案为:39°12′.
13.解:根据题意得:(5x+2y)﹣(6x﹣3y)=5x+2y﹣6x+3y=﹣x+5y,
故答案为:﹣x+5y
14.解:由题意知:第四小组的频数=50﹣(2+8+15+5)=20,
故答案为:20
15.解:∵|x﹣1|=﹣x+1且|x﹣1|≥0,
∴﹣x+1≥0,
∴x≤1,
故答案为:0(答案不唯一)
16.解:多项式﹣2m3+3m2﹣m的各项系数之积为:
﹣2×3×(﹣)=3.
故答案为:3.
17.解:根据题意得:
∠AOC+∠DOB
=∠AOB+∠BOC+∠DOB
=∠AOB+∠COD
=90°+90°
=180°,
故答案为:180°.
18.解:图中的线段有:
线段AB,线段AC,线段AD,线段BC,线段BD,线段CD,共6条.
故答案为:6.
19.解:∵第1个图形中点的个数8=2×1+6,
第2个图形中点的个数10=2×2+6,
第3个图形中点的个数12=2×3+6,
第4个图形中点的个数14=2×4+6,
……
∴第n个图形中点的个数为2n+6,
故答案为:2n+6.
20.解:设AB=x,则BC=2x,CD=3x,CE=DE=CD=x,
∵BE=BC+CE=2x+x=14,
∴x=4.
∵点F为线段AD的三等分点,
∴AF=AD=2x或DF=AD=2x.
当AF=2x时,如图1所示,EF=AB+BC+CE﹣AF=x=10;
当DF=2x时,如图2所示,EF=DF﹣DE==2.
综上,线段EF的长为2或10.
故答案为:2或10.
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.解:(1)原式=(﹣+﹣)×24=﹣16+12﹣15=﹣19;
(2)原式=﹣4××=﹣.
22.解:原式=x﹣2x+y2﹣x+y2
=﹣3x+y2
当x=﹣1,y=时,
原式=﹣3×(﹣1)+
=
23.解:(1)如图所示:
(2)解:设这个角是x度,则
180﹣x=3(90﹣x)﹣50,
解得:x=20,
答:这个角是20度.
24.解:(1)本次调查的学生人数为25÷25%=100(名);
(2)八年级的人数为100×20%=20人,则六年级的人数为100﹣(25+20+25)=30,
补全图形如下:
六年级所对应扇形的圆心角的度数为360°×=108°;
(3)估计全市六、七年级的学生一共有2.8×=1.54(万人).
25.解:(1)由题意可知:∠AOB=180°,∠BOD=30°,
∠AOD=∠AOB﹣∠BOD=150°,
∵∠AOD=∠AOC+∠COD,∠COD=∠AOC,
∴∠AOC+∠AOC=150°,
∴∠AOC=70°;
(2)由图可见:∠AON+20°=∠COM,
故:答案为:∠AON+20°=∠COM;
(3)证明:∵∠AOC=70°,∠AOB=180°,
∴∠BOC=∠AOB﹣∠AOC=110°,
∵OM是∠BOC的角平分线
∴∠COM=∠BOC=55°,
∵∠MON=90°,
∴∠CON=∠MON﹣∠COM=35°,
∵∠AOC=70°,
∴∠AON=∠AOC﹣∠CON=35°,
∴∠AON=∠CON.
26.解:(1)∵m与互为倒数,
∴m==2.8.
故答案为:2.8;
(2)2.8+0.2+0.1﹣0.1﹣0.4+0.3+0.5﹣0.1=3.3(万册).
答:活动结束时,该教育集团所捐图书存量为3.3万册;
(3)设A运输公司每天运输x万册图书,则B运输公司每天运输1.5x万册图书,
根据题意得:2x+(6﹣2)[(1﹣25%)x+1.5x]=3.3,
解得:x=0.3.
答:A运输公司每天运输0.3万册图书.
27.解:(1)∵m、n满足关于x、y的整式x41+myn+60与2xy3m之和是单项式,
∴41+m=1,n+60=3n,
解得:m=﹣40,n=30.
(2)∵点A、B所对应的数分别为﹣40和30,
∴AB=70,AO=40,BO=30.
当点P在O的左侧时,PA+PO=AO=40,PB=AB﹣AP=70﹣4t.
∵PB﹣(PA+PO)=10,
∴70﹣4t﹣40=10,
∴t=5;
当点P在O的右侧时,∵PB<PA,
∴PB﹣(PA+PO)<0,不合题意,舍去.
(3)运动时间为t秒时,点P表示的数为4t﹣40,点Q表示的数为30﹣2t,
∵PQ=AB,
∴|30﹣2t﹣(4t﹣40)|=×70,
解得:t=或t=.
当t=时,AP=4t=;
当t=时,AP=4t=70.
答:若PQ=AB,则AP的长为或70.
同课章节目录
