湖北省潜江市江汉油田2017-2018学年(五四学制)六年级(下)期末数学试卷解析版
文档属性
| 名称 | 湖北省潜江市江汉油田2017-2018学年(五四学制)六年级(下)期末数学试卷解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 187.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-06 00:00:00 | ||
图片预览




文档简介
湖北省潜江市江汉油田2017-2018学年(五四学制)六年级(下)期末数学试卷
一、选择题:(每小题3分,共30分)(请将正确答案的字母代号写在选择题答题栏中)
1.下列算式中,运算结果为负数的是( )
A.﹣(﹣1) B.|﹣1| C.(﹣1)2 D.(﹣1)3
2.据中新网报道,“神威?太湖之光”获吉尼斯世界纪录认证,成为世界上“运算速度最快的计算机”,它共有40960块处理器.其中40960用科学记数法可表示为( )
A.0.4096×105 B.4.096×104 C.4.0960×103 D.40.96×103
3.有理数m,n在数轴上的对应点的位置如图所示,则正确的结论是( )
A.m<﹣1 B.n>3 C.m<﹣n D.m>﹣n
4.已知x=2是关于x的一元一次方程mx+2=0的解,则m的值为( )
A.﹣1 B.0 C.1 D.2
5.下列计算正确的是( )
A.7a+a=7a2 B.3x2y﹣2x2y=x2y
C.5y﹣3y=2 D.3a+2b=5ab
6.下列判断正确的是( )
A.﹣<﹣
B.x﹣1是有理数,它的倒数是
C.若|a|=|b|,则a=b
D.若|a|=﹣a,则a<0
7.如图,左面的平面图形绕轴旋转一周,可以得到的立体图形是( )
A. B. C. D.
8.下列说法:
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
其中说法正确的是( )
A.①② B.②③ C.②④ D.③④
9.在春节到来之际,某童装推出系列活动,一位妈妈看好两件衣服,她想给孩子都买下来作为新年礼物,与店员商量希望都以60元的价格卖给她.销售员发现这样一件就会盈利25%,另一件就会亏损25%,如果这样卖出去,那么商店( )
A.不盈不亏 B.盈利50元 C.盈利8元 D.亏损8元
10.如图,一副三角尺按不同的位置摆放,摆放位置中∠α=∠β的图形有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:(每小题3分,共18分)
11.如果x﹣2y=3,那么代数式1+2x﹣4y的值是 .
12.请写出一个只含有字母m、n,且次数为3的单项式 .
13.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b= .
14.如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.AC=3cm,CP=1cm,线段PN= cm.
15.观察下列图形:它们是按一定规律排列的,依照此规律,第n个(n为正整数)图形中共有五角星的个数为 .
16.按下面的程序计算:
若输入大于3的正整数x的值,输出结果是150,则满足条件的x的值为 .
三、解答题:(9小题,共72分)
17.(8分)(1)计算:﹣﹣+
(2)计算:(﹣1)10﹣8÷(﹣2)+4×|﹣5|
18.(5分)先化简,再求值:2x3﹣(7x2﹣9x)﹣2(x3﹣3x2+4x),其中x=﹣1.
19.(5分)已知线段a、b,用尺规作一条线段AB,使得AB=3a﹣b.不写作法,保留作图痕迹.
20.(8分)解方程
(1)3(4x﹣5)+2=3x;
(2).
21.(8分)某电动车厂计划一周生产电动车1400辆,平均每天计划生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.如表是某周的生产情况:(超过每天计划生产数记为正、不足每天计划生产数记为负):
星期 一 二 三 四 五 六 日
增减 +5 ﹣2 ﹣4 +13 ﹣10 +14 ﹣9
(1)该厂星期三生产电动车 辆;
(2)产量最多的一天比产量最少的一天多生产电动车 辆;
(3)该厂本周实际每天平均生产多少辆电动车?
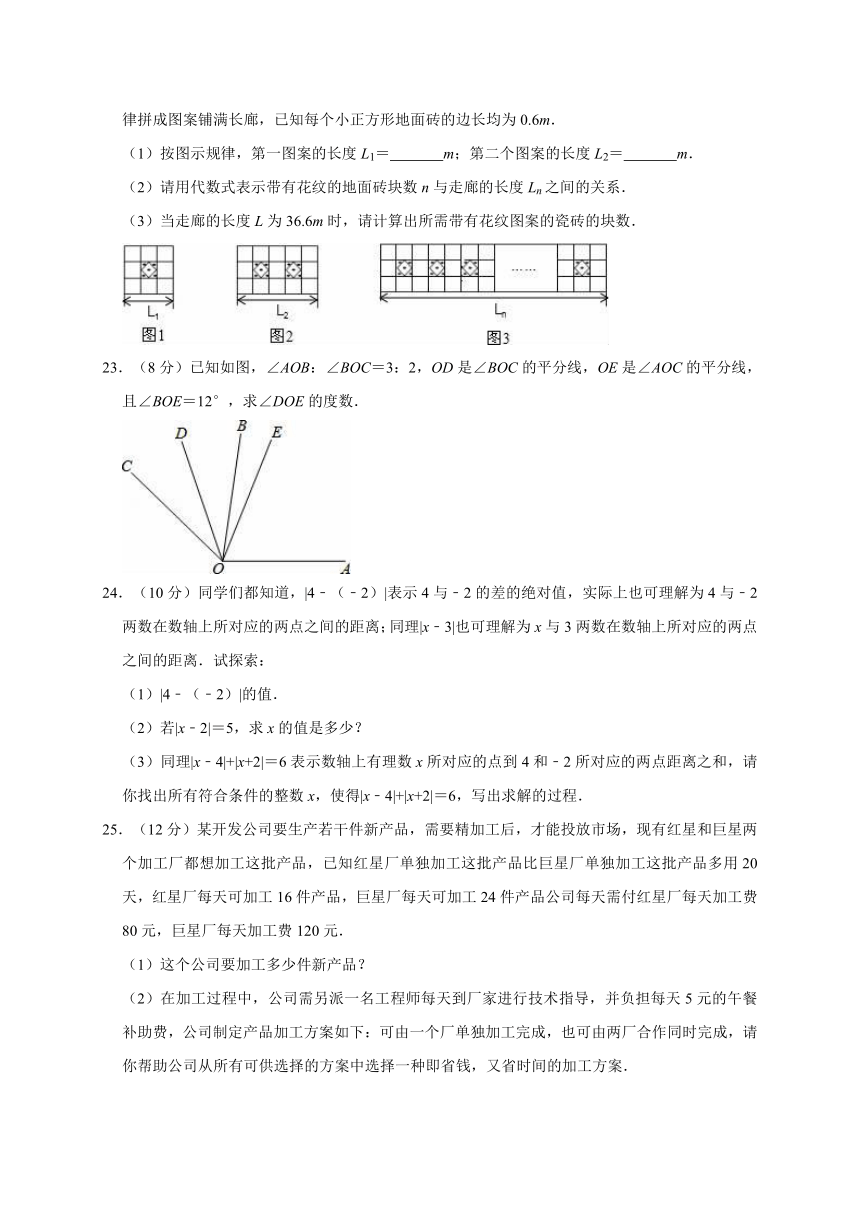
22.(8分)为给同学们创造更好的读书条件,学校准备新建一个长度为L的度数长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.
(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.
(3)当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数.
23.(8分)已知如图,∠AOB:∠BOC=3:2,OD是∠BOC的平分线,OE是∠AOC的平分线,且∠BOE=12°,求∠DOE的度数.
24.(10分)同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)|4﹣(﹣2)|的值.
(2)若|x﹣2|=5,求x的值是多少?
(3)同理|x﹣4|+|x+2|=6表示数轴上有理数x所对应的点到4和﹣2所对应的两点距离之和,请你找出所有符合条件的整数x,使得|x﹣4|+|x+2|=6,写出求解的过程.
25.(12分)某开发公司要生产若干件新产品,需要精加工后,才能投放市场,现有红星和巨星两个加工厂都想加工这批产品,已知红星厂单独加工这批产品比巨星厂单独加工这批产品多用20天,红星厂每天可加工16件产品,巨星厂每天可加工24件产品公司每天需付红星厂每天加工费80元,巨星厂每天加工费120元.
(1)这个公司要加工多少件新产品?
(2)在加工过程中,公司需另派一名工程师每天到厂家进行技术指导,并负担每天5元的午餐补助费,公司制定产品加工方案如下:可由一个厂单独加工完成,也可由两厂合作同时完成,请你帮助公司从所有可供选择的方案中选择一种即省钱,又省时间的加工方案.
参考答案与试题解析
一、选择题:(每小题3分,共30分)(请将正确答案的字母代号写在选择题答题栏中)
1.解:﹣(﹣1)=1>0,运算结果为正;
|﹣1|=1>0,运算结果为正;
(﹣1)2=1>0,运算结果为正;
(﹣1)3=﹣1<0,运算结果为负.
故选:D.
2.解:40960用科学记数法可表示为4.096×104.
故选:B.
3.解:由数轴可得,
﹣1<m<0<2<n<3,故选项A错误,选项B错误,
∴m>﹣n,故选项C错误,选项D正确,
故选:D.
4.解:把x=2代入方程得:2m+2=0,
解得:m=﹣1,
故选:A.
5.解:(A)原式=8a,故A错误;
(C)原式=2y,故C错误;
(D)3a与2b不是同类项,故D错误;
故选:B.
6.解:∵>,
∴﹣<﹣,故A正确.
当x=1时,x﹣1=0,0不存在倒数,故B错误;
若|a|=|b|,则a=±b,故C错误;
若|a|=﹣a,则a≤0,故D错误.
故选:A.
7.解:梯形绕下底边旋转是圆锥加圆柱,故C正确;
故选:C.
8.解:①射线AB和射线BA不是同一条射线,错误;
②若AB=BC,点B在线段AC上时,则点B为线段AC的中点,错误;
③同角的补角相等,正确;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10,正确.
故选:D.
9.解:设盈利25%的那件衣服的进价是x元,亏损25%的那件衣服的进价是y元,由题意得:
x(1+25%)=60,y(1﹣25%)=60,
解得:x=48,y=80,
故60×2﹣48﹣80=﹣8.
故选:D.
10.解:根据角的和差关系可得第一个图形∠α=∠β=45°,
根据同角的余角相等可得第二个图形∠α=∠β,
根据等角的补角相等可得第三个图形∠α=∠β,
第四个图形∠α+∠β=180°,不相等,
因此∠α=∠β的图形个数共有3个.
故选:C.
二、填空题:(每小题3分,共18分)
11.解:∵x﹣2y=3,
∴原式=1+2(x﹣2y)=1+6=7,
故答案为:7
12.解:先构造系数,例如为﹣2,然后使m、n的指数和是3即可.如﹣2m2n,答案不唯一.
故答案是:﹣2m2n(答案不唯一).
13.解:这是一个正方体的平面展开图,共有六个面,其中面“a”与面“1”相对,面“b”与面“3”相对,“2”与面“﹣2”相对.
因为相对面上两个数都互为相反数,
所以a=﹣1,b=﹣3,
故a+b=﹣4.
14.解:∵AP=AC+CP,CP=1cm,
∴AP=3+1=4cm,
∵P为AB的中点,
∴AB=2AP=8cm,
∵CB=AB﹣AC,AC=3cm,
∴CB=5cm,
∵N为CB的中点,
∴CN=BC=cm,
∴PN=CN﹣CP=cm.
故答案为:.
15.解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第n个图形中共有3n+1个图形;
故答案为:(3n+1).
16.解:当一次输入正好输出150时,
即4x﹣2=150,
解得,x=38.
当返回一次输入正好输出150时,
即4(4x﹣2)﹣2=150,
解得x=10.
当返回二次输入正好输出150时,
4[4(4x﹣2)﹣2]﹣2=150,
x的解不为正整数.
故答案为:38或10.
三、解答题:(9小题,共72分)
17.解:(1)﹣﹣+
=
=
=;
(2)(﹣1)10﹣8÷(﹣2)+4×|﹣5|
=1+4+4×5
=1+4+20
=25.
18.解:原式=﹣x2+x(4分),当x=﹣1时,原式=﹣2.
19.解:如图所示,线段AB即为所求.
20.解:(1)去括号,得:12x﹣15+2=3x,
移项,得:12x﹣3x=15﹣2,
合并同类项,得:9x=13,
系数化为1,得:x=;
(2)去分母,得:2(2x﹣5)﹣6(3x+1)=12,
去括号,得:4x﹣10﹣18x﹣6=12,
移项,得:4x﹣18x=12+10+6,
合并同类项,得:﹣14x=28,
系数化为1,得:x=﹣2.
21.解:(1)200+(﹣4)=196(辆)
(2)14﹣(﹣10)=24(辆)
(3)(5﹣2﹣4+13﹣10+14﹣9)÷7+200=201(辆)
答:该厂本周实际每天平均生产201辆自行车;
故答案为:196;24.
22.解:(1)第一图案的长度L1=0.6×3=1.8,第二个图案的长度L2=0.6×5=3;
故答案为:1.8,3;
(2)观察图形可得:
第1个图案中有花纹的地面砖有1块,
第2个图案中有花纹的地面砖有2块,
…
则第n个图案中有花纹的地面砖有n块;
第一个图案边长L=3×0.6,第二个图案边长L=5×0.6,则第n个图案边长为L=(2n+1)×0.6;
(3)把L=36.6代入L=(2n+1)×0.6中得:
36.6=(2n+1)×0.6,
解得:n=30,
答:需带有花纹图案的瓷砖的块数是30.
23.解:设∠AOB=3x,∠BOC=2x.
则∠AOC=∠AOB+∠BOC=5x.
∵OE是∠AOC的平分线,
∴∠AOE═,
∴∠BOE=∠AOB﹣∠AOE=,
∵∠BOE=12°,
∴,
解得,x=24°,
∵OD是∠BOC的平分线,
∴,
∴∠DOE=∠DOB+∠BOE=24°+12°=36°.
24.解:(1)∵4与﹣2两数在数轴上所对应的两点之间的距离是6,
∴|4﹣(﹣2)|=6.
(2)|x﹣2|=5表示x与2两数在数轴上所对应的两点之间的距离是5,
∵﹣3或7与2两数在数轴上所对应的两点之间的距离是5,
∴若|x﹣2|=5,则x=﹣3或7.
(3)∵4与﹣2两数在数轴上所对应的两点之间的距离是6,
∴使得|x﹣4|+|x+2|=6成立的整数是﹣2和4之间的所有整数(包括﹣2和4),
∴这样的整数是﹣2、﹣1、0、1、2、3、4.
25.解:(1)设这个公司要加工x件新产品,由题意得:﹣=20,
解得:x=960(件),
答:这个公司要加工960件新产品.
(2)①由红星厂单独加工:需要耗时为=60天,需要费用为:60×(5+80)=5100元;
②由巨星厂单独加工:需要耗时为=40天,需要费用为:40×(120+5)=5000元;
③由两场厂共同加工:需要耗时为=24天,需要费用为:24×(80+120+5)=4920元.
所以,由两厂合作同时完成时,既省钱,又省时间.
一、选择题:(每小题3分,共30分)(请将正确答案的字母代号写在选择题答题栏中)
1.下列算式中,运算结果为负数的是( )
A.﹣(﹣1) B.|﹣1| C.(﹣1)2 D.(﹣1)3
2.据中新网报道,“神威?太湖之光”获吉尼斯世界纪录认证,成为世界上“运算速度最快的计算机”,它共有40960块处理器.其中40960用科学记数法可表示为( )
A.0.4096×105 B.4.096×104 C.4.0960×103 D.40.96×103
3.有理数m,n在数轴上的对应点的位置如图所示,则正确的结论是( )
A.m<﹣1 B.n>3 C.m<﹣n D.m>﹣n
4.已知x=2是关于x的一元一次方程mx+2=0的解,则m的值为( )
A.﹣1 B.0 C.1 D.2
5.下列计算正确的是( )
A.7a+a=7a2 B.3x2y﹣2x2y=x2y
C.5y﹣3y=2 D.3a+2b=5ab
6.下列判断正确的是( )
A.﹣<﹣
B.x﹣1是有理数,它的倒数是
C.若|a|=|b|,则a=b
D.若|a|=﹣a,则a<0
7.如图,左面的平面图形绕轴旋转一周,可以得到的立体图形是( )
A. B. C. D.
8.下列说法:
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
其中说法正确的是( )
A.①② B.②③ C.②④ D.③④
9.在春节到来之际,某童装推出系列活动,一位妈妈看好两件衣服,她想给孩子都买下来作为新年礼物,与店员商量希望都以60元的价格卖给她.销售员发现这样一件就会盈利25%,另一件就会亏损25%,如果这样卖出去,那么商店( )
A.不盈不亏 B.盈利50元 C.盈利8元 D.亏损8元
10.如图,一副三角尺按不同的位置摆放,摆放位置中∠α=∠β的图形有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:(每小题3分,共18分)
11.如果x﹣2y=3,那么代数式1+2x﹣4y的值是 .
12.请写出一个只含有字母m、n,且次数为3的单项式 .
13.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b= .
14.如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.AC=3cm,CP=1cm,线段PN= cm.
15.观察下列图形:它们是按一定规律排列的,依照此规律,第n个(n为正整数)图形中共有五角星的个数为 .
16.按下面的程序计算:
若输入大于3的正整数x的值,输出结果是150,则满足条件的x的值为 .
三、解答题:(9小题,共72分)
17.(8分)(1)计算:﹣﹣+
(2)计算:(﹣1)10﹣8÷(﹣2)+4×|﹣5|
18.(5分)先化简,再求值:2x3﹣(7x2﹣9x)﹣2(x3﹣3x2+4x),其中x=﹣1.
19.(5分)已知线段a、b,用尺规作一条线段AB,使得AB=3a﹣b.不写作法,保留作图痕迹.
20.(8分)解方程
(1)3(4x﹣5)+2=3x;
(2).
21.(8分)某电动车厂计划一周生产电动车1400辆,平均每天计划生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.如表是某周的生产情况:(超过每天计划生产数记为正、不足每天计划生产数记为负):
星期 一 二 三 四 五 六 日
增减 +5 ﹣2 ﹣4 +13 ﹣10 +14 ﹣9
(1)该厂星期三生产电动车 辆;
(2)产量最多的一天比产量最少的一天多生产电动车 辆;
(3)该厂本周实际每天平均生产多少辆电动车?
22.(8分)为给同学们创造更好的读书条件,学校准备新建一个长度为L的度数长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.
(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.
(3)当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数.
23.(8分)已知如图,∠AOB:∠BOC=3:2,OD是∠BOC的平分线,OE是∠AOC的平分线,且∠BOE=12°,求∠DOE的度数.
24.(10分)同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:
(1)|4﹣(﹣2)|的值.
(2)若|x﹣2|=5,求x的值是多少?
(3)同理|x﹣4|+|x+2|=6表示数轴上有理数x所对应的点到4和﹣2所对应的两点距离之和,请你找出所有符合条件的整数x,使得|x﹣4|+|x+2|=6,写出求解的过程.
25.(12分)某开发公司要生产若干件新产品,需要精加工后,才能投放市场,现有红星和巨星两个加工厂都想加工这批产品,已知红星厂单独加工这批产品比巨星厂单独加工这批产品多用20天,红星厂每天可加工16件产品,巨星厂每天可加工24件产品公司每天需付红星厂每天加工费80元,巨星厂每天加工费120元.
(1)这个公司要加工多少件新产品?
(2)在加工过程中,公司需另派一名工程师每天到厂家进行技术指导,并负担每天5元的午餐补助费,公司制定产品加工方案如下:可由一个厂单独加工完成,也可由两厂合作同时完成,请你帮助公司从所有可供选择的方案中选择一种即省钱,又省时间的加工方案.
参考答案与试题解析
一、选择题:(每小题3分,共30分)(请将正确答案的字母代号写在选择题答题栏中)
1.解:﹣(﹣1)=1>0,运算结果为正;
|﹣1|=1>0,运算结果为正;
(﹣1)2=1>0,运算结果为正;
(﹣1)3=﹣1<0,运算结果为负.
故选:D.
2.解:40960用科学记数法可表示为4.096×104.
故选:B.
3.解:由数轴可得,
﹣1<m<0<2<n<3,故选项A错误,选项B错误,
∴m>﹣n,故选项C错误,选项D正确,
故选:D.
4.解:把x=2代入方程得:2m+2=0,
解得:m=﹣1,
故选:A.
5.解:(A)原式=8a,故A错误;
(C)原式=2y,故C错误;
(D)3a与2b不是同类项,故D错误;
故选:B.
6.解:∵>,
∴﹣<﹣,故A正确.
当x=1时,x﹣1=0,0不存在倒数,故B错误;
若|a|=|b|,则a=±b,故C错误;
若|a|=﹣a,则a≤0,故D错误.
故选:A.
7.解:梯形绕下底边旋转是圆锥加圆柱,故C正确;
故选:C.
8.解:①射线AB和射线BA不是同一条射线,错误;
②若AB=BC,点B在线段AC上时,则点B为线段AC的中点,错误;
③同角的补角相等,正确;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10,正确.
故选:D.
9.解:设盈利25%的那件衣服的进价是x元,亏损25%的那件衣服的进价是y元,由题意得:
x(1+25%)=60,y(1﹣25%)=60,
解得:x=48,y=80,
故60×2﹣48﹣80=﹣8.
故选:D.
10.解:根据角的和差关系可得第一个图形∠α=∠β=45°,
根据同角的余角相等可得第二个图形∠α=∠β,
根据等角的补角相等可得第三个图形∠α=∠β,
第四个图形∠α+∠β=180°,不相等,
因此∠α=∠β的图形个数共有3个.
故选:C.
二、填空题:(每小题3分,共18分)
11.解:∵x﹣2y=3,
∴原式=1+2(x﹣2y)=1+6=7,
故答案为:7
12.解:先构造系数,例如为﹣2,然后使m、n的指数和是3即可.如﹣2m2n,答案不唯一.
故答案是:﹣2m2n(答案不唯一).
13.解:这是一个正方体的平面展开图,共有六个面,其中面“a”与面“1”相对,面“b”与面“3”相对,“2”与面“﹣2”相对.
因为相对面上两个数都互为相反数,
所以a=﹣1,b=﹣3,
故a+b=﹣4.
14.解:∵AP=AC+CP,CP=1cm,
∴AP=3+1=4cm,
∵P为AB的中点,
∴AB=2AP=8cm,
∵CB=AB﹣AC,AC=3cm,
∴CB=5cm,
∵N为CB的中点,
∴CN=BC=cm,
∴PN=CN﹣CP=cm.
故答案为:.
15.解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第n个图形中共有3n+1个图形;
故答案为:(3n+1).
16.解:当一次输入正好输出150时,
即4x﹣2=150,
解得,x=38.
当返回一次输入正好输出150时,
即4(4x﹣2)﹣2=150,
解得x=10.
当返回二次输入正好输出150时,
4[4(4x﹣2)﹣2]﹣2=150,
x的解不为正整数.
故答案为:38或10.
三、解答题:(9小题,共72分)
17.解:(1)﹣﹣+
=
=
=;
(2)(﹣1)10﹣8÷(﹣2)+4×|﹣5|
=1+4+4×5
=1+4+20
=25.
18.解:原式=﹣x2+x(4分),当x=﹣1时,原式=﹣2.
19.解:如图所示,线段AB即为所求.
20.解:(1)去括号,得:12x﹣15+2=3x,
移项,得:12x﹣3x=15﹣2,
合并同类项,得:9x=13,
系数化为1,得:x=;
(2)去分母,得:2(2x﹣5)﹣6(3x+1)=12,
去括号,得:4x﹣10﹣18x﹣6=12,
移项,得:4x﹣18x=12+10+6,
合并同类项,得:﹣14x=28,
系数化为1,得:x=﹣2.
21.解:(1)200+(﹣4)=196(辆)
(2)14﹣(﹣10)=24(辆)
(3)(5﹣2﹣4+13﹣10+14﹣9)÷7+200=201(辆)
答:该厂本周实际每天平均生产201辆自行车;
故答案为:196;24.
22.解:(1)第一图案的长度L1=0.6×3=1.8,第二个图案的长度L2=0.6×5=3;
故答案为:1.8,3;
(2)观察图形可得:
第1个图案中有花纹的地面砖有1块,
第2个图案中有花纹的地面砖有2块,
…
则第n个图案中有花纹的地面砖有n块;
第一个图案边长L=3×0.6,第二个图案边长L=5×0.6,则第n个图案边长为L=(2n+1)×0.6;
(3)把L=36.6代入L=(2n+1)×0.6中得:
36.6=(2n+1)×0.6,
解得:n=30,
答:需带有花纹图案的瓷砖的块数是30.
23.解:设∠AOB=3x,∠BOC=2x.
则∠AOC=∠AOB+∠BOC=5x.
∵OE是∠AOC的平分线,
∴∠AOE═,
∴∠BOE=∠AOB﹣∠AOE=,
∵∠BOE=12°,
∴,
解得,x=24°,
∵OD是∠BOC的平分线,
∴,
∴∠DOE=∠DOB+∠BOE=24°+12°=36°.
24.解:(1)∵4与﹣2两数在数轴上所对应的两点之间的距离是6,
∴|4﹣(﹣2)|=6.
(2)|x﹣2|=5表示x与2两数在数轴上所对应的两点之间的距离是5,
∵﹣3或7与2两数在数轴上所对应的两点之间的距离是5,
∴若|x﹣2|=5,则x=﹣3或7.
(3)∵4与﹣2两数在数轴上所对应的两点之间的距离是6,
∴使得|x﹣4|+|x+2|=6成立的整数是﹣2和4之间的所有整数(包括﹣2和4),
∴这样的整数是﹣2、﹣1、0、1、2、3、4.
25.解:(1)设这个公司要加工x件新产品,由题意得:﹣=20,
解得:x=960(件),
答:这个公司要加工960件新产品.
(2)①由红星厂单独加工:需要耗时为=60天,需要费用为:60×(5+80)=5100元;
②由巨星厂单独加工:需要耗时为=40天,需要费用为:40×(120+5)=5000元;
③由两场厂共同加工:需要耗时为=24天,需要费用为:24×(80+120+5)=4920元.
所以,由两厂合作同时完成时,既省钱,又省时间.
同课章节目录
