山东省东营市垦利区2017-2018学年(五四学制)六年级(下)期末数学试卷解析版
文档属性
| 名称 | 山东省东营市垦利区2017-2018学年(五四学制)六年级(下)期末数学试卷解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-06 00:00:00 | ||
图片预览



文档简介
山东省东营市垦利区2017-2018学年(五四学制)六年级(下)期末数学试卷
一、选择题(本题共10个小题,每小题3分,共30分.将正确答案的字母填入括号中)
1.下列调查中,调查方式选择正确的是( )
A.为了了解生产的50枚炮弹的杀伤半径,选择普查
B.为了了解某公园全年的游客流量,选择普查
C.要了解某电视台“最强大脑”栏目的收视率,采用抽样调查
D.要保证“神舟十号”载人飞船发射成功,对重要零部件的检查采用抽样调查
2.如果A、B、C在同一条直线上,线段AB=5cm,BC=4cm,则A、C两点间的距离是( )
A.9cm B.1cm C.9cm或1cm D.无法确定
3.如图,O为直线AB上一点,∠COB=28°34′,则∠1=( )
A.151°26′ B.161°26′ C.151°34′ D.161°34′
4.如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
A.3 cm B.6 cm C.11 cm D.14 cm
5.钟表在5时30分,它的时针和分针所成的锐角是( )
A.90° B.70° C.30° D.15°
6.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
7.计算(2x3y)2的结果是( )
A.4x6y2 B.8x6y2 C.4x5y2 D.8x5y2
8.如果x2+mx+1恰好是一个整式的平方,那么常数m的值是( )
A.?1 B.?2 C.±1? D.±2?
9.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
10.李老师骑车外出办事,离校不久便接到学校要他返校的紧急电话,李老师急忙赶回学校、下面四个图象中,描述李老师与学校距离的图象是( )
A. B.
C. D.
二、填空题(本题共8个小题,共28分.其中11-14题每题3分,15-18题每题4分.)
11.计算20180﹣2﹣1= .
12.将一个圆分割成三个扇形,它们圆心角度数之间的关系为2:3:4,则这三个扇形中圆心角最小的度数是 度.
13.若am=3,an=5,则am﹣n= .
14.x+y=1009,x﹣y=2,则代数式x2﹣y2= .
15.(4分)如图,AC平分∠DAB,∠1=∠2.填空:因为AC平分∠DAB,所以∠1= .所以∠2= .所以AB∥ .根据是 .
16.(4分)由东营南到德州的某一次列车,运行途中停靠的车站依次是:东营南﹣﹣滨州﹣﹣阳信﹣﹣商河﹣﹣德州,那么要为这次列车制作的火车票有 种.
17.(4分)汽车开始行使时,油箱中有油50升,如果每小时耗油4升,则油箱内余油量y(升)与行使时间x(小时)的关系式为 .
18.(4分)观察下列关于自然数的等式:
32﹣4×12=5 ①
52﹣4×22=9 ②
72﹣4×32=13 ③…
根据上述规律请你猜想的第n个等式为 (用含n的式子表示).
三、解答题(本大题共7个小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.)
19.(4分)画图题
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,问货场应建在什么位置,使货场到A、B两厂的距离之和最小?在图中标出货场位置,并说明理由.
20.(8分)计算
(1)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x
(2)982﹣4(用乘法公式)
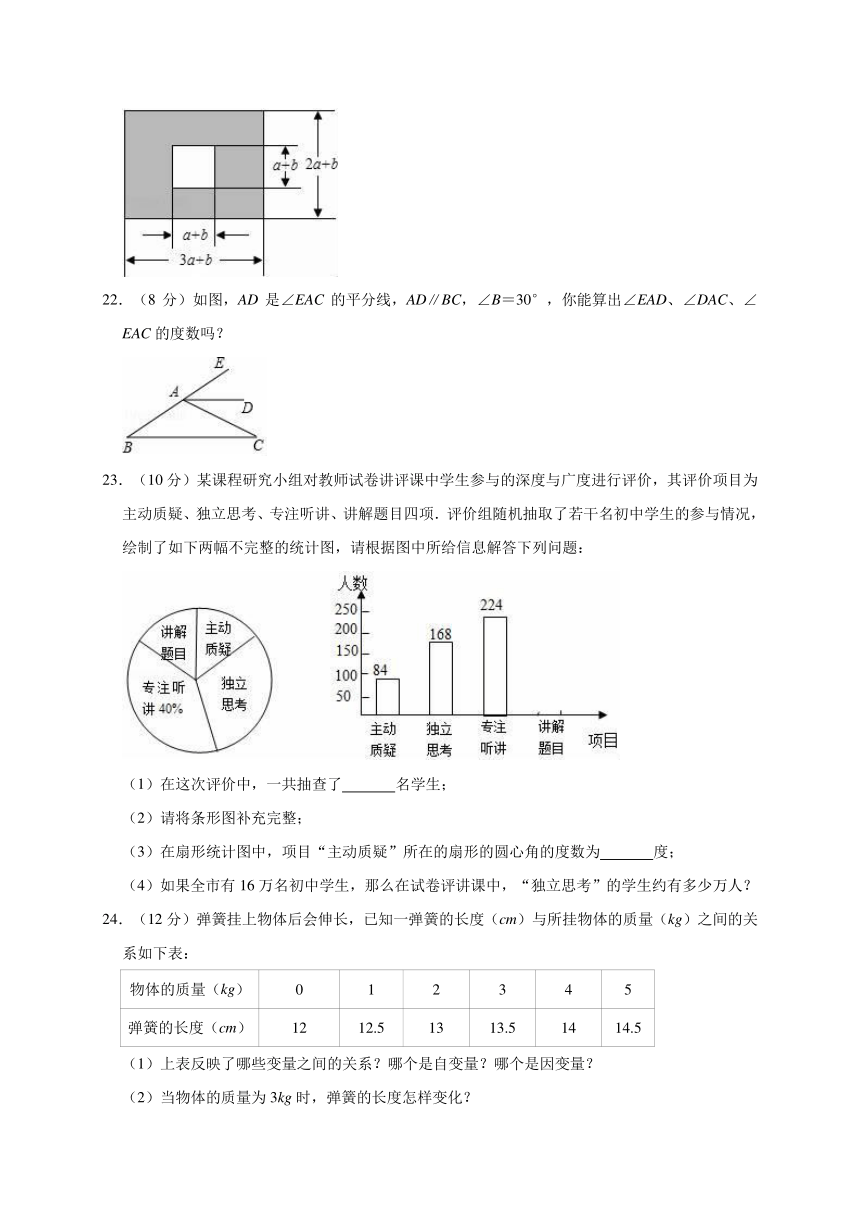
21.(8分)如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
22.(8分)如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,你能算出∠EAD、∠DAC、∠EAC的度数吗?
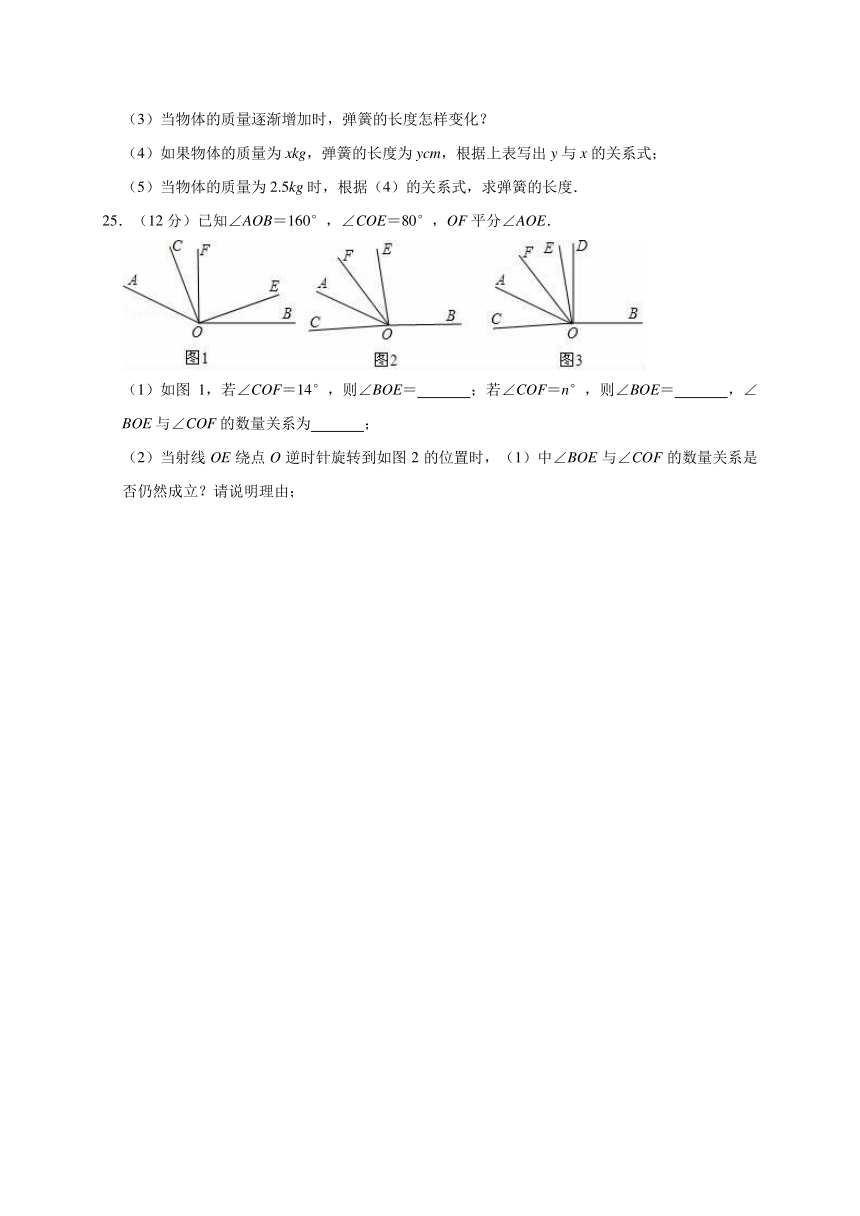
23.(10分)某课程研究小组对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(4)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
24.(12分)弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) 0 1 2 3 4 5
弹簧的长度(cm) 12 12.5 13 13.5 14 14.5
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
25.(12分)已知∠AOB=160°,∠COE=80°,OF平分∠AOE.
(1)如图1,若∠COF=14°,则∠BOE= ;若∠COF=n°,则∠BOE= ,∠BOE与∠COF的数量关系为 ;
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由;
参考答案与试题解析
一、选择题(本题共10个小题,每小题3分,共30分.将正确答案的字母填入括号中)
1.解:A、为了了解生产的50枚炮弹的杀伤半径,适合抽样调查,此选项错误;
B、为了了解某公园全年的游客流量,适合抽样调查,此选项错误;
C、要了解某电视台“最强大脑”栏目的收视率,采用抽样调查,此选项正确;
D、要保证“神舟十号”载人飞船发射成功,对重要零部件的检查采用全面调查,此选项错误;
故选:C.
2.解:如图:1:当点C在点B的右侧时,AC=AB+BC=5+4=9(cm).
如图2:当点C在AB之间时,AC=AB﹣BC=5﹣4=1(cm);
故选:C.
3.解:∵O为直线AB上一点,
∴∠1=180°﹣∠COB,
而∠COB=28°34′,
∴∠1=180°﹣28°34′=151°26′.
故选:A.
4.解:∵C,D是线段AB上两点,CB=4cm,DB=7cm,
∴CD=DB﹣BC=7﹣4=3(cm),
∵D是AC的中点,
∴AC=2CD=2×3=6(cm).
故选:B.
5.解:根据分析可知:时针和分针所成的锐角为×30°=15°.
故选:D.
6.解:①两点之间的所有连线中,线段最短,故①正确.
②相等的角不一定是对顶角,故②错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.
⑤两点之间的距离是两点间的线段的长度,故⑤错误.
⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.
综上所述,正确的结论有2个.
故选:B.
7.解:(2x3y)2=4x6y2.
故选:A.
8.解:∵(x±1)2=x2±2x+1,
∴在x2+mx+1中,±2x=mx,
解得m=±2.
故选:D.
9.解:∵∠DPF=∠BAF,
∴AB∥PD(同位角相等,两直线平行).
故选:A.
10.解:李老师从学校出发离校,接到电话前,距离是随着时间的增加而增加的,接到电话后,开始返校,距离是随着时间的增加而减少的,故舍去A、B选项,又返回时是急忙返校,所以与来时同样的距离,返回时用的时间较少,所以C正确.
故选:C.
二、填空题(本题共8个小题,共28分.其中11-14题每题3分,15-18题每题4分.)
11.解:原式=1﹣=,
故答案为:
12.解:∵周角的度数是360°,
∴这三个扇形中圆心角最小的度数是,
故答案为:80.
13.解:∵am=3,an=5,
∴am﹣n=am÷an=3÷5=,
故答案为:.
14.解:∵x+y=1009,x﹣y=2,
∴原式=(x+y)(x﹣y)=2018,
故答案为:2018
15.解:∵AC平分∠DAB,
∴∠1=∠CAB.
又∵∠1=∠2,
∴∠CAB=∠2,
∴AB∥CD(内错角相等,两直线平行).
故答案为:∠CAB,∠CAB,CD,内错角相等,两直线平行.
16.解:如图,设东营南﹣﹣滨州﹣﹣阳信﹣﹣商河﹣﹣德州五站分别用A、B、C、D、E表示,
则共有线段:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10条,
所以,需要制作火车票10×2=20种.
故答案为:20.
17.解:依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=50﹣4x.
故答案为:y=50﹣4x.
18.解:(1)32﹣4×12=5 ①
52﹣4×22=9 ②
72﹣4×32=13 ③
…
所以第n个等式为:(2n+1)2﹣4n2=4n+1,
故答案为:(2n+1)2﹣4n2=4n+1.
三、解答题(本大题共7个小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.)
19.解:点C即为货场位置,
理由:两点之间,线段最短.
20.解:(1)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x
=[x2+4xy+4y2﹣(3x2﹣xy+3xy﹣y2)﹣5y2]÷2x
=(x2+4xy+4y2﹣3x2+xy﹣3xy+y2﹣5y2)÷2x
=(﹣2x2+2xy)÷2x
=﹣x+y;
(2)982﹣4
=(98+2)(98﹣2)
=9600.
21.解:阴影部分的面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab,
当a=3,b=2时,原式=5×32+3×3×2=63(平方米).
22.解:因为AD∥BC,
所以∠EAD=∠B=30°,
因为AD是∠EAC的平分线,
所以∠DAC=∠EAD=30°,
所以∠EAC=∠EAD+∠DAC=30°+30°=60°.
23.解:(1)由题意可得出:专注听讲的人数为:224,专注听讲的在扇形统计图中所占比例为:40%,
故在这次评价中,一共抽查的学生人数为:224÷40%=560;
故答案为:560;
(2)由(1)得:讲解题目的人数为:560﹣84﹣168﹣224=84(人),
如图所示:
;
(3)扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为360°×=54°,
故答案为:54.
(4)∵本市有16万名初中学生,
∴在试卷评讲课中,“独立思考”的学生约有:16×=4.8(万人),
答:“独立思考”的学生约有4.8万人.
24.解:(1)反映了物体的质量与弹簧的长度之间的关系,物体的质量是自变量,弹簧的长度是因变量;
(2)弹簧的长度由原来的12cm变为13.5cm;
(3)当物体的质量逐渐增加时,弹簧的长度逐渐变长;
(4)y=12+0.5x;
(5)当x=2.5时,y=12+0.5×2.5=13.25(cm).
25.解:(1)∵∠AOE=∠AOB﹣∠BOE,
而OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
而∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF,
当∠COF=14°时,∠BOE=28°;当∠COF=n°时,∠BOE=2n°,
故答案为:28°;2n°;∠BOE=2∠COF.
(2)∠BOE=2∠COF仍然成立.理由如下:
∵∠AOE=∠AOB﹣∠BOE,
而OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
而∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF.
一、选择题(本题共10个小题,每小题3分,共30分.将正确答案的字母填入括号中)
1.下列调查中,调查方式选择正确的是( )
A.为了了解生产的50枚炮弹的杀伤半径,选择普查
B.为了了解某公园全年的游客流量,选择普查
C.要了解某电视台“最强大脑”栏目的收视率,采用抽样调查
D.要保证“神舟十号”载人飞船发射成功,对重要零部件的检查采用抽样调查
2.如果A、B、C在同一条直线上,线段AB=5cm,BC=4cm,则A、C两点间的距离是( )
A.9cm B.1cm C.9cm或1cm D.无法确定
3.如图,O为直线AB上一点,∠COB=28°34′,则∠1=( )
A.151°26′ B.161°26′ C.151°34′ D.161°34′
4.如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
A.3 cm B.6 cm C.11 cm D.14 cm
5.钟表在5时30分,它的时针和分针所成的锐角是( )
A.90° B.70° C.30° D.15°
6.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
7.计算(2x3y)2的结果是( )
A.4x6y2 B.8x6y2 C.4x5y2 D.8x5y2
8.如果x2+mx+1恰好是一个整式的平方,那么常数m的值是( )
A.?1 B.?2 C.±1? D.±2?
9.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
10.李老师骑车外出办事,离校不久便接到学校要他返校的紧急电话,李老师急忙赶回学校、下面四个图象中,描述李老师与学校距离的图象是( )
A. B.
C. D.
二、填空题(本题共8个小题,共28分.其中11-14题每题3分,15-18题每题4分.)
11.计算20180﹣2﹣1= .
12.将一个圆分割成三个扇形,它们圆心角度数之间的关系为2:3:4,则这三个扇形中圆心角最小的度数是 度.
13.若am=3,an=5,则am﹣n= .
14.x+y=1009,x﹣y=2,则代数式x2﹣y2= .
15.(4分)如图,AC平分∠DAB,∠1=∠2.填空:因为AC平分∠DAB,所以∠1= .所以∠2= .所以AB∥ .根据是 .
16.(4分)由东营南到德州的某一次列车,运行途中停靠的车站依次是:东营南﹣﹣滨州﹣﹣阳信﹣﹣商河﹣﹣德州,那么要为这次列车制作的火车票有 种.
17.(4分)汽车开始行使时,油箱中有油50升,如果每小时耗油4升,则油箱内余油量y(升)与行使时间x(小时)的关系式为 .
18.(4分)观察下列关于自然数的等式:
32﹣4×12=5 ①
52﹣4×22=9 ②
72﹣4×32=13 ③…
根据上述规律请你猜想的第n个等式为 (用含n的式子表示).
三、解答题(本大题共7个小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.)
19.(4分)画图题
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,问货场应建在什么位置,使货场到A、B两厂的距离之和最小?在图中标出货场位置,并说明理由.
20.(8分)计算
(1)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x
(2)982﹣4(用乘法公式)
21.(8分)如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
22.(8分)如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,你能算出∠EAD、∠DAC、∠EAC的度数吗?
23.(10分)某课程研究小组对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(4)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
24.(12分)弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) 0 1 2 3 4 5
弹簧的长度(cm) 12 12.5 13 13.5 14 14.5
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
25.(12分)已知∠AOB=160°,∠COE=80°,OF平分∠AOE.
(1)如图1,若∠COF=14°,则∠BOE= ;若∠COF=n°,则∠BOE= ,∠BOE与∠COF的数量关系为 ;
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由;
参考答案与试题解析
一、选择题(本题共10个小题,每小题3分,共30分.将正确答案的字母填入括号中)
1.解:A、为了了解生产的50枚炮弹的杀伤半径,适合抽样调查,此选项错误;
B、为了了解某公园全年的游客流量,适合抽样调查,此选项错误;
C、要了解某电视台“最强大脑”栏目的收视率,采用抽样调查,此选项正确;
D、要保证“神舟十号”载人飞船发射成功,对重要零部件的检查采用全面调查,此选项错误;
故选:C.
2.解:如图:1:当点C在点B的右侧时,AC=AB+BC=5+4=9(cm).
如图2:当点C在AB之间时,AC=AB﹣BC=5﹣4=1(cm);
故选:C.
3.解:∵O为直线AB上一点,
∴∠1=180°﹣∠COB,
而∠COB=28°34′,
∴∠1=180°﹣28°34′=151°26′.
故选:A.
4.解:∵C,D是线段AB上两点,CB=4cm,DB=7cm,
∴CD=DB﹣BC=7﹣4=3(cm),
∵D是AC的中点,
∴AC=2CD=2×3=6(cm).
故选:B.
5.解:根据分析可知:时针和分针所成的锐角为×30°=15°.
故选:D.
6.解:①两点之间的所有连线中,线段最短,故①正确.
②相等的角不一定是对顶角,故②错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.
⑤两点之间的距离是两点间的线段的长度,故⑤错误.
⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.
综上所述,正确的结论有2个.
故选:B.
7.解:(2x3y)2=4x6y2.
故选:A.
8.解:∵(x±1)2=x2±2x+1,
∴在x2+mx+1中,±2x=mx,
解得m=±2.
故选:D.
9.解:∵∠DPF=∠BAF,
∴AB∥PD(同位角相等,两直线平行).
故选:A.
10.解:李老师从学校出发离校,接到电话前,距离是随着时间的增加而增加的,接到电话后,开始返校,距离是随着时间的增加而减少的,故舍去A、B选项,又返回时是急忙返校,所以与来时同样的距离,返回时用的时间较少,所以C正确.
故选:C.
二、填空题(本题共8个小题,共28分.其中11-14题每题3分,15-18题每题4分.)
11.解:原式=1﹣=,
故答案为:
12.解:∵周角的度数是360°,
∴这三个扇形中圆心角最小的度数是,
故答案为:80.
13.解:∵am=3,an=5,
∴am﹣n=am÷an=3÷5=,
故答案为:.
14.解:∵x+y=1009,x﹣y=2,
∴原式=(x+y)(x﹣y)=2018,
故答案为:2018
15.解:∵AC平分∠DAB,
∴∠1=∠CAB.
又∵∠1=∠2,
∴∠CAB=∠2,
∴AB∥CD(内错角相等,两直线平行).
故答案为:∠CAB,∠CAB,CD,内错角相等,两直线平行.
16.解:如图,设东营南﹣﹣滨州﹣﹣阳信﹣﹣商河﹣﹣德州五站分别用A、B、C、D、E表示,
则共有线段:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10条,
所以,需要制作火车票10×2=20种.
故答案为:20.
17.解:依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=50﹣4x.
故答案为:y=50﹣4x.
18.解:(1)32﹣4×12=5 ①
52﹣4×22=9 ②
72﹣4×32=13 ③
…
所以第n个等式为:(2n+1)2﹣4n2=4n+1,
故答案为:(2n+1)2﹣4n2=4n+1.
三、解答题(本大题共7个小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.)
19.解:点C即为货场位置,
理由:两点之间,线段最短.
20.解:(1)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x
=[x2+4xy+4y2﹣(3x2﹣xy+3xy﹣y2)﹣5y2]÷2x
=(x2+4xy+4y2﹣3x2+xy﹣3xy+y2﹣5y2)÷2x
=(﹣2x2+2xy)÷2x
=﹣x+y;
(2)982﹣4
=(98+2)(98﹣2)
=9600.
21.解:阴影部分的面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab,
当a=3,b=2时,原式=5×32+3×3×2=63(平方米).
22.解:因为AD∥BC,
所以∠EAD=∠B=30°,
因为AD是∠EAC的平分线,
所以∠DAC=∠EAD=30°,
所以∠EAC=∠EAD+∠DAC=30°+30°=60°.
23.解:(1)由题意可得出:专注听讲的人数为:224,专注听讲的在扇形统计图中所占比例为:40%,
故在这次评价中,一共抽查的学生人数为:224÷40%=560;
故答案为:560;
(2)由(1)得:讲解题目的人数为:560﹣84﹣168﹣224=84(人),
如图所示:
;
(3)扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为360°×=54°,
故答案为:54.
(4)∵本市有16万名初中学生,
∴在试卷评讲课中,“独立思考”的学生约有:16×=4.8(万人),
答:“独立思考”的学生约有4.8万人.
24.解:(1)反映了物体的质量与弹簧的长度之间的关系,物体的质量是自变量,弹簧的长度是因变量;
(2)弹簧的长度由原来的12cm变为13.5cm;
(3)当物体的质量逐渐增加时,弹簧的长度逐渐变长;
(4)y=12+0.5x;
(5)当x=2.5时,y=12+0.5×2.5=13.25(cm).
25.解:(1)∵∠AOE=∠AOB﹣∠BOE,
而OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
而∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF,
当∠COF=14°时,∠BOE=28°;当∠COF=n°时,∠BOE=2n°,
故答案为:28°;2n°;∠BOE=2∠COF.
(2)∠BOE=2∠COF仍然成立.理由如下:
∵∠AOE=∠AOB﹣∠BOE,
而OF平分∠AOE,
∴∠AOE=2∠EOF,
∴2∠EOF=∠AOB﹣∠BOE,
∴2(∠COE﹣∠COF)=∠AOB﹣∠BOE,
而∠AOB=160°,∠COE=80°,
∴160°﹣2∠COF=160°﹣∠BOE,
∴∠BOE=2∠COF.
同课章节目录
