高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):31【基础】直线、圆的位置关系
文档属性
| 名称 | 高中数学必修二知识讲解,巩固练习(复习补习,期末复习资料):31【基础】直线、圆的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 457.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-07 00:00:00 | ||
图片预览




文档简介
直线、圆的位置关系
【学习目标】
1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系;
2.能用直线和圆的方程解决一些简单的问题;
3.在平面解析几何初步的学习过程中,体会用代数方法处理几何问题的思想.
【要点梳理】
要点一:直线与圆的位置关系
1.直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2.直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
要点诠释:
(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.
(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.
(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.
要点二:圆的切线方程的求法
1.点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率
的乘积等于,即.
法二:圆心到直线的距离等于半径.
2.点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
要点诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是.
要点三:求直线被圆截得的弦长的方法
1.应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
2.利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
3.利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:=.
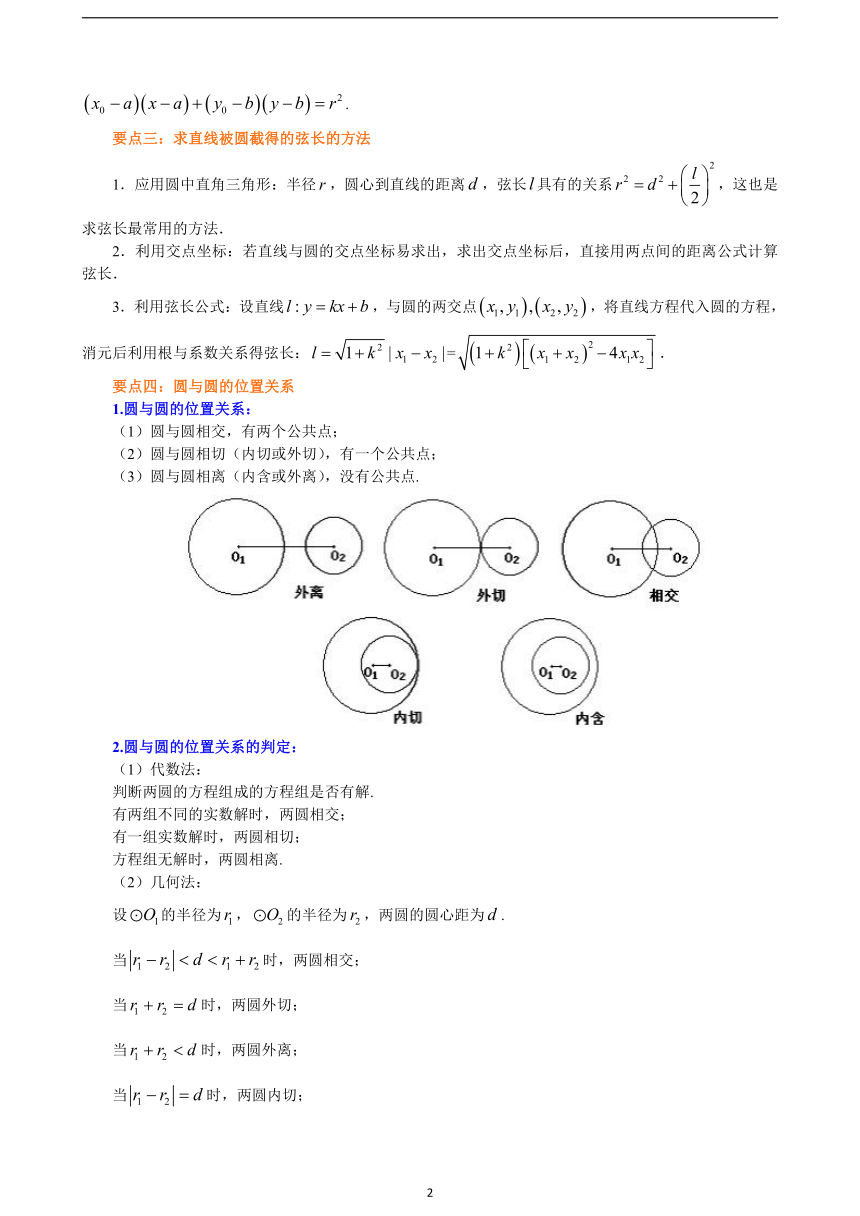
要点四:圆与圆的位置关系
1.圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
2.圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
要点诠释:
判定圆与圆的位置关系主要是利用几何法,通过比较两圆的圆心距和两圆的半径的关系来确定,这种方法运算量小.也可利用代数法,但是利用代数法解决时,一是运算量大,二是方程组仅有一解或无解时,两圆的位置关系不明确,还要比较两圆的圆心距和两圆半径的关系来确定.因此,在处理圆与圆的位置关系时,一般不用代数法.
3.两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
4.两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
【典型例题】
类型一:直线与圆的位置关系
例1.已知直线y=2x+1和圆x2+y2=4,试判断直线和圆的位置关系.
【思路点拨】解决本题的方法主要有两个,其一是利用圆心到直线的距离与半径的大小关系;其二是引入一元二次方程,利用方程根来解决.
【答案】相交
【解析】
解法一:∵x2+y2=4,
∴圆心为(0,0),半径r=2.
又∵y=2x+1,∴圆心到直线的距离为.∴直线与圆相交.
解法二:∵ ∴(2x+1)2+x2=4,
即5x2+4x-3=0.
判别式Δ=42-4×5×(-3)=76>0.
∴直线与圆相交.
【总结升华】判断直线与圆的位置关系可以从代数方法和几何意义两个方面加以考虑.
例2.已知直线方程mx―y―m―1=0,圆的方程x2+y2―4x―2y+1=0.当m为何值时,圆与直线
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
【答案】(1)m>0或(2)m=0或(3)
【解析】解法一:将直线mx―y―m―1=0代入圆的方程化简整理得,
(1+m2)x2―2(m2+2m+2)x+m2+4m+4=0.
∵Δ=4m(3m+4),
∴当Δ>0时,即m>0或时,直线与圆相交,即直线与圆有两个公共点;
当Δ=0时,即m=0或时,直线与圆相切,即直线与圆只有一个公共点;
当Δ<时,即时,直线与圆相离,即直线与圆没有公共点.
解法二:已知圆的方程可化为(x―2)2+(y―1)2=4,
即圆心为C(2,1),半径r=2.
圆心C(2,1)到直线mx―y―m―1=0的距离
.
当d<2时,即m>0或时,直线与圆相交,即直线与圆有两个公共点;
当d=2时,即m=0或时,直线与圆相切,即直线与圆只有一个公共点;
当d>2时,即时,直线与圆相离,即直线与圆没有公共点.
【总结升华】解决此类问题是搞清直线与圆的位置和直线与圆的公共点的个数间的等价关系.在处理直线与圆的位置关系时,常用几何法,即比较圆心到直线的距离和半径的大小,而不用联立方程.
举一反三:
【变式1】求实数m的范围,使直线与圆分别满足:
(1)相交;(2)相切;(3)相离.
【答案】(1)或(2)(3)
【解析】圆的方程化为标准为,故圆心(3,0)到直线的距离,圆的半径.
(1)若相交,则,即,所以或.
(2)若相切,则,即,所以.
(3)若相离,则,即,所以.
【总结升华】一般来讲,选择此方法要比选择计算判别式的方法在运算上简单.
类型二:切线问题
例3.过点作圆的切线,求切线的方程.
【思路点拨】先判断点在圆上或圆外,如果点在圆上则有一条切线.如果点在圆外,则有两条切线.本例中很明显点在圆外.
【答案】或
【解析】
因为,所以点在圆外.
法一:设过点与圆相切的直线为,即.
因为圆心到的距离,则,即.解得
或.
从而,切线方程为或.
解法二:设过点与圆相切的直线为.
由可得.从而
.
解得或.
从而,切线方程为或.
【总结升华】求圆的切线方程一般有三种方法:
(1)直接法:应用常见结论,直接写出切线方程;
(2)待定系数法;
(3)定义法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.
举一反三:
【变式1】(2018 天津河西区模拟)已知圆C经过点A(2,0)、,且圆心C在直线y=x上.
(1)求圆C的方程;
(2)过点的直线l截圆所得弦长为,求直线l的方程.
【答案】(1)x2+y2=4;(2)x=1或
【解析】(1)AB的中点坐标,AB的斜率为.可得AB垂直平分线为,与x―y=0的交点为(0,0),圆心坐标(0,0),半径为2,
所以圆C的方程为x2+y2=4;
(2)直线的斜率存在时,设直线的斜率为k,又直线l过,
∴直线l的方程为,即,
则圆心(0,0)到直线的距离,又圆的半径r=2,截得的弦长为,
则有,
解得:,
则直线l的方程为.
当直线的斜率不存在时,直线方程为x=1,满足题意.
直线l的方程:x=1或.
【总结升华】此题考查了直线与圆相交的性质,涉及的知识有点到直线的距离公式,垂径定理及勾股定理,当直线与圆相交时,常常利用弦长的一半,圆的半径及弦心距构造直角三角形来解决问题.
类型三:弦长问题
例4.直线经过点P(5,5)并且与圆C:x2+y2=25相交截得的弦长为,求的方程.
【答案】x―2y+5=0或2x―y―5=0
【解析】法一:根据题意知直线的斜率存在,设直线的方程为y―5=k(x―5)
圆心(0,0)到直线的距离,在由弦长的一半、半径和距离构成的直角三角形中,
,解得或k=2
故直线的方程为x―2y+5=0或2x―y―5=0.
法二:根据题意知直线的斜率存在,
设直线的方程为y―5=k(x―5)与圆C相交于A(x1,y1),B(x2,y2),
联立方程,消去y,得(k2+1)x2+10k(1―k)x+25k(k―2)=0,
∴Δ=[10k(1―k)]2―4(k2+1)·25k(k―2)>0,解得k>0.
又,.
由斜率公式,得y1―y2=k(x1―x2),
∴
.
两边平方,整理得2k2―5k+2=0,
解得或k=2,符合题意.
故直线的方程为x―2y+5=0或2x―y―5=0.
【总结升华】 设直线的方程为ax+by+c=0,圆O的方程为(x―x0)2+(y―y0)2=r2,求弦长的方法有以下两种:
(1)几何法:由圆的性质知,过圆心O作的垂线,垂足C为线段AB的中点.如图所示,在Rt△OCB中,|BC|2=r2―d2.
则弦长|AB|=2|BC|,即.
(2)代数法:解方程组,
消元后可得关于x1+x2,x1·x2或y1+y2,y1·y2的关系式,则
举一反三:
【变式1】求经过点P(6,―4),且被定圆x2+y2=20截得弦长为的直线的方程.
【答案】x+y―2=0或7x+17y+26=0
【解析】如图所示,,,作OC⊥AB于C.在Rt△OAC中,.
设所求直线的斜率为k,则直线的方程为y+4=k(x―6),即kx―y―6k―4=0.又圆到直线的距离为,
∴,即17k2+24k+7=0,∴k1=―1,.
∴所求直线方程为x+y―2=0或7x+17y+26=0.
类型四:圆与圆的位置关系
例5.已知圆C1:x2+y2―2mx+4y+m2―5=0,圆C2:x2+y2+2x―2my+m2―3=0,问:m为何值时,(1)圆C1和圆C2相外切?(2)圆C1与圆C2内含?
【思路点拨】利用几何法或代数法都可以判断.
【答案】(1)m=―5或m=2;(2)―2<m<―1.
【解析】对于圆C1,圆C2的方程,配方得
C1:(x―m)2+(y+2)2=9,C2:(x+1)2+(y―m)2=4.
(1)如果圆C1与圆C2相外切,则有,即
(m+1)2+(m+2)2=25,m2+3m―10=0,
解得m=―5或m=2.
(2)如果圆C1与圆C2内含,则有,即
(m+1)2+(m+2)2<1,m2+3m+2<0,解得―2<m<―1.
故(1)当m=―5或m=2时,圆C1与圆C2相外切;(2)当―2<m<―1时,圆C1与圆C2内含.
【总结升华】利用几何法判定两圆的位置关系比用代数法(即解两圆方程联立方程组的方法)要简捷些,但需要注意的是,我们这里所说的几何法仍然是在解析几何前提下的几何法,即利用圆的方程及两点间距离公式求出两圆圆心距d和两圆的半径R和r,再根据d与R+r、d与R―r的大小关系来判定即可.
举一反三:
【变式1】当a为何值时,圆C1:x2+y2―2ax+4y+(a2―5)=0和圆C2:x2+y2+2x―2ay+(a2―3)=0相交.
【答案】当―5<a<―2或―1<a<2时,圆C1与圆C2相交
【变式2】已知圆:,圆:,求两圆公共弦所在的直线方程及公共弦的长.
【思路点拨】对两圆的方程作差即可得出两圆的公共弦所在的直线方程,再由点到直线的距离公式求出一个圆的圆心到该弦的距离,用弦心距、弦的一半,半径建立的直角三角形求出弦的一半,即得其长.
【答案】公共弦所在直线方程为3x―4y+6=0,弦长为
【解析】两圆的方程作差得6x―8y+12=0,即3x―4y+6=0,
∵圆:,故其圆心为(―1,3),r=3
圆到弦所在直线的距离为
弦长的一半是
故弦长为
综上,公共弦所在直线方程为3x―4y+6=0,弦长为.
类型五:最值问题
例6.已知实数x、y满足方程x2+y2―4x+1=0,
求:(1)的最大值;(2)y―x的最小值.
【思路点拨】将x2+y2―4x+1=0、、y―x赋予几何意义,利用数形结合来解决.
【答案】(1)(2)
【解析】
将实数x、y看作点P(x,y)的坐标,满足x2+y2―4x+1=0的点P(x,y)组成的图形是以M(2,0)为圆心,半径为的圆,如图所示.
(1)设,即是圆上的点P与原点O连线的斜率.
由图知,直线y=kx和圆M在第一象限相切时,k取最大值.
此时有OP⊥PM,,|OM|=2,∴∠POM=60°
此时,∴的最大值为.
(2)设y―x=b,则y=x+b,b是直线y=x+b在y轴上截距.由图知,当直线y=x+b和圆M在第四象限相切时,b(b<0)取最小值,此时有,解得,
∴y―x的最小值是.
【总结升华】利用数形结合解决最值问题时,首先从代数演算入手,将代数表达式赋予几何意义,看成某几何量的大小,根据图形的几何性质,观察出最值出现的时机和位置,从而解决求代数表达式的最值问题.这是用几何方法解决代数问题的常用方法,即数形结合.常见的数形结合点是直线方程、圆的方程、过两点的斜率公式、平面内两点间距离公式、直线在y轴上的截距等.
举一反三:
【变式1】已知点P(x,y)在圆上,求的最小值.
【答案】
【解析】设,则k的几何意义为圆上的点与原点的斜率,
则由图象可知当直线y=kx与圆在第二象限相切时,直线斜率最小,此时k<0,
则圆心(-2,0)到直线的距离,
即,解得,
故的最小值为.
【变式2】已知实数x,y满足,求(1)x2+y2的最大值;(2)x+y的最小值.
【答案】(1)16 (2)
【解析】
于是(x,y)可以看作是以为圆心,2为半径的圆上的点.
如图
(1)x2+y2可看作是圆上的点到原点的距离的平方,
由图显然最大为2r=4,所以x2+y2的最大值为16.
(2)解法同例6(2).
【巩固练习】
1.已知圆C1:x2+y2=4,圆C2:x2+y2+6x―4y=0,则两圆的位置关系是( )
A.相切 B.相离 C.相交 D.内含
2.两圆x2+y2―2x+10y―24=0与x2+y2+2x+2y―8=0的交点坐标为( )
A.(4,0)或(2,0) B.(―4,0)或(2,0)
C.(―4,0)或(0,2) D.(4,0)或(0,―2)
3.直线与圆交于两点,则线段的垂直平分线的方程是( )
A. B.
C. D.
4.直线截圆得到的劣弧所对的圆心角为( )
A. B. C. D.
5.直线l:y=k(x+1)与圆:在第一象限内部分的图象有交点,k的取值范围( )
A. B. C. D.0<k<5
6.过点(―4,0)作直线与圆x2+y2+2x―4y―20=0交于A、B两点,若|AB|=8,则( )
A.的斜率为
B.的方程为5x―12y+20=0
C.的方程为5x+12y+20=0或x+4=0
D.的方程为5x―12y+20=0或x+4=0
7.(2018 安徽黄山一模)设圆C:x2+y2―2x―2y―m=0一直线y=x―4相切,则圆C的半径为( )
A. B.10 C.6 D.
8.若圆上恰有相异两点到直线的距离等于1,则的取值范围是( )
A. B. C. D.
9.两圆x2+y2+2x―4y+3=0与x2+y2―4x+2y+3=0上的点之间的最短距离是________。
10.若直线l过点且被圆截得的弦长为8,则直线l的方程是 .
11.已知圆C过点(1,0),且圆心在x轴的正半轴上,直线:y=x―1被圆C所截得的弦长为,则过圆心且与直线垂直的直线的方程为________。
12.是圆上任意一点,则的最大值是 ;点到直线的最大距离是 。
13.(2018春 吉林期末)如图所示,在Rt△ABC中,已知A(―2,0),直角顶点,点C在x轴上.
(1)求Rt△ABC外接圆的方程;
(2)求过点(―4,0)且与Rt△ABC外接圆相切的直线的方程.
14.(1)已知圆:,圆:,试判断圆与圆的位置关系.
(2)已知圆心为C的圆经过点A(1,2)和B(2,―2),且圆心在l:x―y+1=0上,求圆C的标准方程.
15.已知A(-3,0),B(3,0),点C为线段AB上任一点,P,Q分别为以AC和BC为直径的两圆,的外公切线的切点.求线段PQ的中点的轨迹方程.
【答案与解析】
1.【答案】C
【解析】圆C1:x2+y2=4,圆心C1(0,0),半径r1=2,圆C2:x2+y2+6x―4y=0,圆心C2(―3,2),半径,∵,∴两圆相交。
2.【答案】C
【解析】通过联立方程组求解即可。
3.【答案】B
4.【答案】C
5.【分析】求得圆和x、y轴的正半轴的交点分别为M(1,0)、.又直线l:y=k(x+1)经过定点A(-1,0),再求出KAM和KAN的值,可得当直线和圆在第一象限内有交点时,直线的斜率k满足的条件.
【答案】C
【解析】圆:即,表示以(―2,0)为圆心,半径等于3的圆.
显然圆和x、y轴的正半轴的交点分别为M(1,0)、.
又直线l:y=k(x+1)经过定点A(―1,0),
KAM=0,,故当直线和圆在第一象限内有交点时,
直线的斜率k满足,
故选:C.
6.【答案】C
【解析】圆心(-1,2),半径r=5,
当直线的斜率存在时,设直线:y=kx+4k。
∵|AB|=8,∴圆心到直线的距离,
解得。∴直线:5x+12y+20=0;
当直线的斜率不存在时,x=―4,代入圆的方程,
y=―2或y=6,即x=―4与圆交于A(―4,―2),B(―4,6),|AB|=8,∴x=―4这条直线也满足题意。
7.【答案】D
【解析】∵圆C:x2+y2―2x―2y―m=0与直线y=x―4相切,
圆C的圆心C(1,1),
∴圆C的半径.
故选D.
8.【答案】C
【解析】∵圆心O(0,0)到直线4x-3y+25=0的距离
,
圆x2+y2=r2(r>0)上恰有相异两点到直线4x-3y+25=0的距离等于1, ∴|d-r|<1,即|5-r|<1, ∴r∈(4,6). 故选B.
9.【答案】
【解析】由x2+y2+2x―4y+3=0,得(x+1)2+(y―1)2=2,由x2+y2―4x+2y+3=0,得(x―2)2+(y+1)2=2,两圆圆心距为,故两圆外离,则两圆上的点之间的最短距离是 。
10.【分析】由圆的方程得到圆的圆心坐标和半径,再结合直线被圆截得的弦长等于8求出圆心到直线的距离,然后分直线的斜率存在和不存在求解直线方程,斜率不存在时直接得答案,斜率存在时由点到直线的距离公式求解.
【答案】x=-3或3x+4y+15=0
【解析】如图,
∵圆的半径为5,直线l被圆截得的半弦长为4,
∴圆心到直线的距离为3.
当直线l过点且斜率不存在时,直线方程为x=―3,满足题意;
当斜率存在时,设斜率为k,则直线的点斜式方程为,
整理得:2kx―2y+6k―3=0.
由圆心(0,0)到直线2kx―2y+6k-3=0的距离等于3得:,
解得:.
∴直线方程为3x+4y+15=0.
综上,直线l的方程是x=-3或3x+4y+15=0.
11.【答案】x+y-3=0
【解析】依题意可设圆心坐标为(a,0),a>0,则半径为|a―1|,圆心到直线的距离为,根据勾股定理可得,,解得a=3或a=―1(舍去),所以圆C的圆心坐标为(3,0),则过圆心且与直线垂直的直线的方程为x+y―3=0。
12.【答案】,6
【解析】的几何意义是点到原点距离的平方。利用这个几何意义求解。
13.【答案】(1)(x―1)2+y2=9;(2)3x―4y+12=0,或3x+4y+12=0.
【解析】(1)设点C(a,0),由BA⊥BC,可得,∴a=4,
故所求的圆的圆心为AC的中点(1,0),半径为,
故要求Rt△ABC外接圆的方程为(x―1)2+y2=9.
(2)由题意可得,要求的直线的斜率一定存在,设要求直线的方程为y=k(x+4),
即kx―y+4k=0,当直线和圆相切时,圆心到直线的距离等于半径,
故有,求得,
故要求的直线的方程为3x―4y+12=0,或3x+4y+12=0.
14.【分析】(1)把圆的方程化为标准形式,求出圆心和半径,根据两圆的圆心距等于3,大于半径之差而小于半径之和,可得两个圆相交.
(2)根据题意设出圆的标准方程,代入点的坐标和圆心位置,解方程组即可.
【解析】(1)由于圆:,即,表示以(―1,―4)为圆心,半径等于5的圆.
圆:,即,表示以(2,2)为圆心,半径等于的圆.
由于两圆的圆心距等于,大于半径之差而小于半径之和,故两个圆相交.
(2)设圆的方程为
则,解得:,
∴圆的方程为
15.【解析】作MC⊥AB交PQ于M,则MC是两圆的公切线,
所以,
所以M为PQ的中点.
设M(x,y),则点C,,的坐标分别为(x,0),,.
连,,则,
所以由勾股定理得,
即PQ中点的轨迹方程为.
【学习目标】
1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系;
2.能用直线和圆的方程解决一些简单的问题;
3.在平面解析几何初步的学习过程中,体会用代数方法处理几何问题的思想.
【要点梳理】
要点一:直线与圆的位置关系
1.直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2.直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
要点诠释:
(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.
(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.
(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.
要点二:圆的切线方程的求法
1.点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率
的乘积等于,即.
法二:圆心到直线的距离等于半径.
2.点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
要点诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是.
要点三:求直线被圆截得的弦长的方法
1.应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
2.利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
3.利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:=.
要点四:圆与圆的位置关系
1.圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
2.圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
要点诠释:
判定圆与圆的位置关系主要是利用几何法,通过比较两圆的圆心距和两圆的半径的关系来确定,这种方法运算量小.也可利用代数法,但是利用代数法解决时,一是运算量大,二是方程组仅有一解或无解时,两圆的位置关系不明确,还要比较两圆的圆心距和两圆半径的关系来确定.因此,在处理圆与圆的位置关系时,一般不用代数法.
3.两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
4.两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
【典型例题】
类型一:直线与圆的位置关系
例1.已知直线y=2x+1和圆x2+y2=4,试判断直线和圆的位置关系.
【思路点拨】解决本题的方法主要有两个,其一是利用圆心到直线的距离与半径的大小关系;其二是引入一元二次方程,利用方程根来解决.
【答案】相交
【解析】
解法一:∵x2+y2=4,
∴圆心为(0,0),半径r=2.
又∵y=2x+1,∴圆心到直线的距离为.∴直线与圆相交.
解法二:∵ ∴(2x+1)2+x2=4,
即5x2+4x-3=0.
判别式Δ=42-4×5×(-3)=76>0.
∴直线与圆相交.
【总结升华】判断直线与圆的位置关系可以从代数方法和几何意义两个方面加以考虑.
例2.已知直线方程mx―y―m―1=0,圆的方程x2+y2―4x―2y+1=0.当m为何值时,圆与直线
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
【答案】(1)m>0或(2)m=0或(3)
【解析】解法一:将直线mx―y―m―1=0代入圆的方程化简整理得,
(1+m2)x2―2(m2+2m+2)x+m2+4m+4=0.
∵Δ=4m(3m+4),
∴当Δ>0时,即m>0或时,直线与圆相交,即直线与圆有两个公共点;
当Δ=0时,即m=0或时,直线与圆相切,即直线与圆只有一个公共点;
当Δ<时,即时,直线与圆相离,即直线与圆没有公共点.
解法二:已知圆的方程可化为(x―2)2+(y―1)2=4,
即圆心为C(2,1),半径r=2.
圆心C(2,1)到直线mx―y―m―1=0的距离
.
当d<2时,即m>0或时,直线与圆相交,即直线与圆有两个公共点;
当d=2时,即m=0或时,直线与圆相切,即直线与圆只有一个公共点;
当d>2时,即时,直线与圆相离,即直线与圆没有公共点.
【总结升华】解决此类问题是搞清直线与圆的位置和直线与圆的公共点的个数间的等价关系.在处理直线与圆的位置关系时,常用几何法,即比较圆心到直线的距离和半径的大小,而不用联立方程.
举一反三:
【变式1】求实数m的范围,使直线与圆分别满足:
(1)相交;(2)相切;(3)相离.
【答案】(1)或(2)(3)
【解析】圆的方程化为标准为,故圆心(3,0)到直线的距离,圆的半径.
(1)若相交,则,即,所以或.
(2)若相切,则,即,所以.
(3)若相离,则,即,所以.
【总结升华】一般来讲,选择此方法要比选择计算判别式的方法在运算上简单.
类型二:切线问题
例3.过点作圆的切线,求切线的方程.
【思路点拨】先判断点在圆上或圆外,如果点在圆上则有一条切线.如果点在圆外,则有两条切线.本例中很明显点在圆外.
【答案】或
【解析】
因为,所以点在圆外.
法一:设过点与圆相切的直线为,即.
因为圆心到的距离,则,即.解得
或.
从而,切线方程为或.
解法二:设过点与圆相切的直线为.
由可得.从而
.
解得或.
从而,切线方程为或.
【总结升华】求圆的切线方程一般有三种方法:
(1)直接法:应用常见结论,直接写出切线方程;
(2)待定系数法;
(3)定义法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.
举一反三:
【变式1】(2018 天津河西区模拟)已知圆C经过点A(2,0)、,且圆心C在直线y=x上.
(1)求圆C的方程;
(2)过点的直线l截圆所得弦长为,求直线l的方程.
【答案】(1)x2+y2=4;(2)x=1或
【解析】(1)AB的中点坐标,AB的斜率为.可得AB垂直平分线为,与x―y=0的交点为(0,0),圆心坐标(0,0),半径为2,
所以圆C的方程为x2+y2=4;
(2)直线的斜率存在时,设直线的斜率为k,又直线l过,
∴直线l的方程为,即,
则圆心(0,0)到直线的距离,又圆的半径r=2,截得的弦长为,
则有,
解得:,
则直线l的方程为.
当直线的斜率不存在时,直线方程为x=1,满足题意.
直线l的方程:x=1或.
【总结升华】此题考查了直线与圆相交的性质,涉及的知识有点到直线的距离公式,垂径定理及勾股定理,当直线与圆相交时,常常利用弦长的一半,圆的半径及弦心距构造直角三角形来解决问题.
类型三:弦长问题
例4.直线经过点P(5,5)并且与圆C:x2+y2=25相交截得的弦长为,求的方程.
【答案】x―2y+5=0或2x―y―5=0
【解析】法一:根据题意知直线的斜率存在,设直线的方程为y―5=k(x―5)
圆心(0,0)到直线的距离,在由弦长的一半、半径和距离构成的直角三角形中,
,解得或k=2
故直线的方程为x―2y+5=0或2x―y―5=0.
法二:根据题意知直线的斜率存在,
设直线的方程为y―5=k(x―5)与圆C相交于A(x1,y1),B(x2,y2),
联立方程,消去y,得(k2+1)x2+10k(1―k)x+25k(k―2)=0,
∴Δ=[10k(1―k)]2―4(k2+1)·25k(k―2)>0,解得k>0.
又,.
由斜率公式,得y1―y2=k(x1―x2),
∴
.
两边平方,整理得2k2―5k+2=0,
解得或k=2,符合题意.
故直线的方程为x―2y+5=0或2x―y―5=0.
【总结升华】 设直线的方程为ax+by+c=0,圆O的方程为(x―x0)2+(y―y0)2=r2,求弦长的方法有以下两种:
(1)几何法:由圆的性质知,过圆心O作的垂线,垂足C为线段AB的中点.如图所示,在Rt△OCB中,|BC|2=r2―d2.
则弦长|AB|=2|BC|,即.
(2)代数法:解方程组,
消元后可得关于x1+x2,x1·x2或y1+y2,y1·y2的关系式,则
举一反三:
【变式1】求经过点P(6,―4),且被定圆x2+y2=20截得弦长为的直线的方程.
【答案】x+y―2=0或7x+17y+26=0
【解析】如图所示,,,作OC⊥AB于C.在Rt△OAC中,.
设所求直线的斜率为k,则直线的方程为y+4=k(x―6),即kx―y―6k―4=0.又圆到直线的距离为,
∴,即17k2+24k+7=0,∴k1=―1,.
∴所求直线方程为x+y―2=0或7x+17y+26=0.
类型四:圆与圆的位置关系
例5.已知圆C1:x2+y2―2mx+4y+m2―5=0,圆C2:x2+y2+2x―2my+m2―3=0,问:m为何值时,(1)圆C1和圆C2相外切?(2)圆C1与圆C2内含?
【思路点拨】利用几何法或代数法都可以判断.
【答案】(1)m=―5或m=2;(2)―2<m<―1.
【解析】对于圆C1,圆C2的方程,配方得
C1:(x―m)2+(y+2)2=9,C2:(x+1)2+(y―m)2=4.
(1)如果圆C1与圆C2相外切,则有,即
(m+1)2+(m+2)2=25,m2+3m―10=0,
解得m=―5或m=2.
(2)如果圆C1与圆C2内含,则有,即
(m+1)2+(m+2)2<1,m2+3m+2<0,解得―2<m<―1.
故(1)当m=―5或m=2时,圆C1与圆C2相外切;(2)当―2<m<―1时,圆C1与圆C2内含.
【总结升华】利用几何法判定两圆的位置关系比用代数法(即解两圆方程联立方程组的方法)要简捷些,但需要注意的是,我们这里所说的几何法仍然是在解析几何前提下的几何法,即利用圆的方程及两点间距离公式求出两圆圆心距d和两圆的半径R和r,再根据d与R+r、d与R―r的大小关系来判定即可.
举一反三:
【变式1】当a为何值时,圆C1:x2+y2―2ax+4y+(a2―5)=0和圆C2:x2+y2+2x―2ay+(a2―3)=0相交.
【答案】当―5<a<―2或―1<a<2时,圆C1与圆C2相交
【变式2】已知圆:,圆:,求两圆公共弦所在的直线方程及公共弦的长.
【思路点拨】对两圆的方程作差即可得出两圆的公共弦所在的直线方程,再由点到直线的距离公式求出一个圆的圆心到该弦的距离,用弦心距、弦的一半,半径建立的直角三角形求出弦的一半,即得其长.
【答案】公共弦所在直线方程为3x―4y+6=0,弦长为
【解析】两圆的方程作差得6x―8y+12=0,即3x―4y+6=0,
∵圆:,故其圆心为(―1,3),r=3
圆到弦所在直线的距离为
弦长的一半是
故弦长为
综上,公共弦所在直线方程为3x―4y+6=0,弦长为.
类型五:最值问题
例6.已知实数x、y满足方程x2+y2―4x+1=0,
求:(1)的最大值;(2)y―x的最小值.
【思路点拨】将x2+y2―4x+1=0、、y―x赋予几何意义,利用数形结合来解决.
【答案】(1)(2)
【解析】
将实数x、y看作点P(x,y)的坐标,满足x2+y2―4x+1=0的点P(x,y)组成的图形是以M(2,0)为圆心,半径为的圆,如图所示.
(1)设,即是圆上的点P与原点O连线的斜率.
由图知,直线y=kx和圆M在第一象限相切时,k取最大值.
此时有OP⊥PM,,|OM|=2,∴∠POM=60°
此时,∴的最大值为.
(2)设y―x=b,则y=x+b,b是直线y=x+b在y轴上截距.由图知,当直线y=x+b和圆M在第四象限相切时,b(b<0)取最小值,此时有,解得,
∴y―x的最小值是.
【总结升华】利用数形结合解决最值问题时,首先从代数演算入手,将代数表达式赋予几何意义,看成某几何量的大小,根据图形的几何性质,观察出最值出现的时机和位置,从而解决求代数表达式的最值问题.这是用几何方法解决代数问题的常用方法,即数形结合.常见的数形结合点是直线方程、圆的方程、过两点的斜率公式、平面内两点间距离公式、直线在y轴上的截距等.
举一反三:
【变式1】已知点P(x,y)在圆上,求的最小值.
【答案】
【解析】设,则k的几何意义为圆上的点与原点的斜率,
则由图象可知当直线y=kx与圆在第二象限相切时,直线斜率最小,此时k<0,
则圆心(-2,0)到直线的距离,
即,解得,
故的最小值为.
【变式2】已知实数x,y满足,求(1)x2+y2的最大值;(2)x+y的最小值.
【答案】(1)16 (2)
【解析】
于是(x,y)可以看作是以为圆心,2为半径的圆上的点.
如图
(1)x2+y2可看作是圆上的点到原点的距离的平方,
由图显然最大为2r=4,所以x2+y2的最大值为16.
(2)解法同例6(2).
【巩固练习】
1.已知圆C1:x2+y2=4,圆C2:x2+y2+6x―4y=0,则两圆的位置关系是( )
A.相切 B.相离 C.相交 D.内含
2.两圆x2+y2―2x+10y―24=0与x2+y2+2x+2y―8=0的交点坐标为( )
A.(4,0)或(2,0) B.(―4,0)或(2,0)
C.(―4,0)或(0,2) D.(4,0)或(0,―2)
3.直线与圆交于两点,则线段的垂直平分线的方程是( )
A. B.
C. D.
4.直线截圆得到的劣弧所对的圆心角为( )
A. B. C. D.
5.直线l:y=k(x+1)与圆:在第一象限内部分的图象有交点,k的取值范围( )
A. B. C. D.0<k<5
6.过点(―4,0)作直线与圆x2+y2+2x―4y―20=0交于A、B两点,若|AB|=8,则( )
A.的斜率为
B.的方程为5x―12y+20=0
C.的方程为5x+12y+20=0或x+4=0
D.的方程为5x―12y+20=0或x+4=0
7.(2018 安徽黄山一模)设圆C:x2+y2―2x―2y―m=0一直线y=x―4相切,则圆C的半径为( )
A. B.10 C.6 D.
8.若圆上恰有相异两点到直线的距离等于1,则的取值范围是( )
A. B. C. D.
9.两圆x2+y2+2x―4y+3=0与x2+y2―4x+2y+3=0上的点之间的最短距离是________。
10.若直线l过点且被圆截得的弦长为8,则直线l的方程是 .
11.已知圆C过点(1,0),且圆心在x轴的正半轴上,直线:y=x―1被圆C所截得的弦长为,则过圆心且与直线垂直的直线的方程为________。
12.是圆上任意一点,则的最大值是 ;点到直线的最大距离是 。
13.(2018春 吉林期末)如图所示,在Rt△ABC中,已知A(―2,0),直角顶点,点C在x轴上.
(1)求Rt△ABC外接圆的方程;
(2)求过点(―4,0)且与Rt△ABC外接圆相切的直线的方程.
14.(1)已知圆:,圆:,试判断圆与圆的位置关系.
(2)已知圆心为C的圆经过点A(1,2)和B(2,―2),且圆心在l:x―y+1=0上,求圆C的标准方程.
15.已知A(-3,0),B(3,0),点C为线段AB上任一点,P,Q分别为以AC和BC为直径的两圆,的外公切线的切点.求线段PQ的中点的轨迹方程.
【答案与解析】
1.【答案】C
【解析】圆C1:x2+y2=4,圆心C1(0,0),半径r1=2,圆C2:x2+y2+6x―4y=0,圆心C2(―3,2),半径,∵,∴两圆相交。
2.【答案】C
【解析】通过联立方程组求解即可。
3.【答案】B
4.【答案】C
5.【分析】求得圆和x、y轴的正半轴的交点分别为M(1,0)、.又直线l:y=k(x+1)经过定点A(-1,0),再求出KAM和KAN的值,可得当直线和圆在第一象限内有交点时,直线的斜率k满足的条件.
【答案】C
【解析】圆:即,表示以(―2,0)为圆心,半径等于3的圆.
显然圆和x、y轴的正半轴的交点分别为M(1,0)、.
又直线l:y=k(x+1)经过定点A(―1,0),
KAM=0,,故当直线和圆在第一象限内有交点时,
直线的斜率k满足,
故选:C.
6.【答案】C
【解析】圆心(-1,2),半径r=5,
当直线的斜率存在时,设直线:y=kx+4k。
∵|AB|=8,∴圆心到直线的距离,
解得。∴直线:5x+12y+20=0;
当直线的斜率不存在时,x=―4,代入圆的方程,
y=―2或y=6,即x=―4与圆交于A(―4,―2),B(―4,6),|AB|=8,∴x=―4这条直线也满足题意。
7.【答案】D
【解析】∵圆C:x2+y2―2x―2y―m=0与直线y=x―4相切,
圆C的圆心C(1,1),
∴圆C的半径.
故选D.
8.【答案】C
【解析】∵圆心O(0,0)到直线4x-3y+25=0的距离
,
圆x2+y2=r2(r>0)上恰有相异两点到直线4x-3y+25=0的距离等于1, ∴|d-r|<1,即|5-r|<1, ∴r∈(4,6). 故选B.
9.【答案】
【解析】由x2+y2+2x―4y+3=0,得(x+1)2+(y―1)2=2,由x2+y2―4x+2y+3=0,得(x―2)2+(y+1)2=2,两圆圆心距为,故两圆外离,则两圆上的点之间的最短距离是 。
10.【分析】由圆的方程得到圆的圆心坐标和半径,再结合直线被圆截得的弦长等于8求出圆心到直线的距离,然后分直线的斜率存在和不存在求解直线方程,斜率不存在时直接得答案,斜率存在时由点到直线的距离公式求解.
【答案】x=-3或3x+4y+15=0
【解析】如图,
∵圆的半径为5,直线l被圆截得的半弦长为4,
∴圆心到直线的距离为3.
当直线l过点且斜率不存在时,直线方程为x=―3,满足题意;
当斜率存在时,设斜率为k,则直线的点斜式方程为,
整理得:2kx―2y+6k―3=0.
由圆心(0,0)到直线2kx―2y+6k-3=0的距离等于3得:,
解得:.
∴直线方程为3x+4y+15=0.
综上,直线l的方程是x=-3或3x+4y+15=0.
11.【答案】x+y-3=0
【解析】依题意可设圆心坐标为(a,0),a>0,则半径为|a―1|,圆心到直线的距离为,根据勾股定理可得,,解得a=3或a=―1(舍去),所以圆C的圆心坐标为(3,0),则过圆心且与直线垂直的直线的方程为x+y―3=0。
12.【答案】,6
【解析】的几何意义是点到原点距离的平方。利用这个几何意义求解。
13.【答案】(1)(x―1)2+y2=9;(2)3x―4y+12=0,或3x+4y+12=0.
【解析】(1)设点C(a,0),由BA⊥BC,可得,∴a=4,
故所求的圆的圆心为AC的中点(1,0),半径为,
故要求Rt△ABC外接圆的方程为(x―1)2+y2=9.
(2)由题意可得,要求的直线的斜率一定存在,设要求直线的方程为y=k(x+4),
即kx―y+4k=0,当直线和圆相切时,圆心到直线的距离等于半径,
故有,求得,
故要求的直线的方程为3x―4y+12=0,或3x+4y+12=0.
14.【分析】(1)把圆的方程化为标准形式,求出圆心和半径,根据两圆的圆心距等于3,大于半径之差而小于半径之和,可得两个圆相交.
(2)根据题意设出圆的标准方程,代入点的坐标和圆心位置,解方程组即可.
【解析】(1)由于圆:,即,表示以(―1,―4)为圆心,半径等于5的圆.
圆:,即,表示以(2,2)为圆心,半径等于的圆.
由于两圆的圆心距等于,大于半径之差而小于半径之和,故两个圆相交.
(2)设圆的方程为
则,解得:,
∴圆的方程为
15.【解析】作MC⊥AB交PQ于M,则MC是两圆的公切线,
所以,
所以M为PQ的中点.
设M(x,y),则点C,,的坐标分别为(x,0),,.
连,,则,
所以由勾股定理得,
即PQ中点的轨迹方程为.
