2019-2020学年高中数学北师大版必修2课件:第二章解析几何初步2.1.1直线的倾斜角和斜率(27张)
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第二章解析几何初步2.1.1直线的倾斜角和斜率(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览







文档简介
课件27张PPT。第二章 解析几何初步§1 直线与直线的方程1.1 直线的倾斜角和斜率1.直线的确定
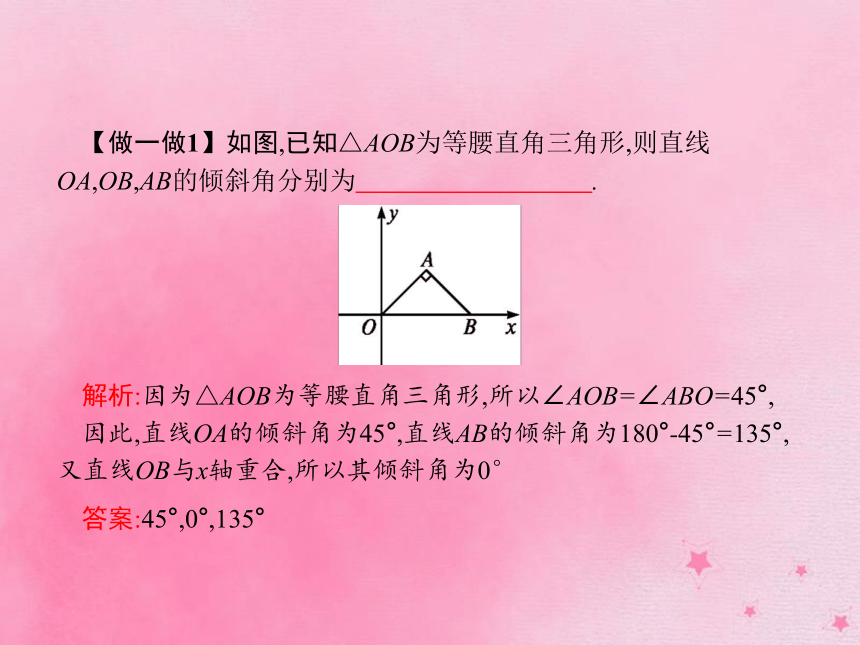
在平面直角坐标系中,确定直线位置的几何条件是:已知直线上的一个点和这条直线的方向2.直线的倾斜角 解析:因为△AOB为等腰直角三角形,所以∠AOB=∠ABO=45°,
因此,直线OA的倾斜角为45°,直线AB的倾斜角为180°-45°=135°,又直线OB与x轴重合,所以其倾斜角为0°答案:45°,0°,135° 【做一做1】如图,已知△AOB为等腰直角三角形,则直线OA,OB,AB的倾斜角分别为 .?3.直线的斜率 4.过两点的直线斜率的计算公式
经过不同的两点P1(x1,y1),P2(x2,y2)的直线的斜率公式是【做一做2】 已知点A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率.解:因为A,B,C三点的横坐标均不相等, 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)直线的倾斜角α的取值范围是[0°,180°]. ( )
(2)直线的倾斜角越大,其斜率也越大. ( )
(3)直线的斜率越大,其倾斜角也越大. ( )
(4)若直线的斜率k=tan θ,则θ一定为该直线的倾斜角. ( )× × × × 探究一探究二探究三易错辨析探究一直线的斜率
【例1】 (1)已知一条直线的倾斜角为60°,求这条直线的斜率;
(2)求经过两点A(2,3),B(m,4)的直线的斜率.
分析:(1)利用斜率的定义求解;(2)对参数m进行分类讨论,分情况求解.探究一探究二探究三易错辨析反思感悟直线斜率的求法
1.求直线的斜率通常有两种方法:一是已知直线的倾斜角α(α≠90°)时,可利用斜率的定义,即k=tan α求得;二是已知直线所经过的两点的坐标时,可利用过两点的直线的斜率公式计算求得.
2.使用斜率公式k= 求斜率时,要注意其前提条件是x1≠x2.若x1=x2,即两点的横坐标相等时,直线的斜率不存在.
3.若两点的横坐标中含有参数,则应先讨论横坐标是否相等,再确定直线的斜率.探究一探究二探究三易错辨析变式训练1若点A(4,2),B(5,b)的连线与点C(1,2),D(3,4)的连线的斜率相等,则b的值为 .?答案:3 探究一探究二探究三易错辨析探究二直线的斜率与倾斜角的简单应用? 【例2】 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.分析:数形结合,利用斜率公式. (1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
(2)由题意可知,直线l的倾斜角在直线PB与PA的倾斜角之间.因为PB的倾斜角是45°,PA的倾斜角是135°,所以α的取值范围是45°≤α≤135°.探究一探究二探究三易错辨析反思感悟1.已知直线的倾斜角的取值范围求斜率的取值范围时,要注意对倾斜角按锐角和钝角两种情况分别进行分析求解;已知斜率的取值范围求倾斜角的取值范围时,应对斜率分正值和负值两种情况分别进行分析求解.探究一探究二探究三易错辨析变式训练2(1)当a为何值时,过点A(2a,3),B(2,-1)的直线的倾斜角是锐角、钝角或直角?
(2)若直线l的斜率k=1,求直线的倾斜角.解:(1)当过点A,B的直线的倾斜角是锐角时,kAB>0, 当倾斜角为直角时,A,B两点的横坐标相等.
即2a=2,所以a=1.
(2)设直线l的倾斜角为α,若k=1,则tan α=1.
又tan 45°=1,且0°<α<180°,所以α=45°.
所以直线的倾斜角为45°.探究一探究二探究三易错辨析探究三利用斜率解决三点共线问题? 反思感悟利用斜率证明三点共线问题的方法步骤: 【例3】 已知三点A(1,-1),B(3,3),C(4,5),求证:A,B,C三点在同一条直线上.又直线AB和BC有公共点B,
所以A,B,C三点共线.探究一探究二探究三易错辨析变式训练3若点A(2,-3),B(4,3),C(5,k)在同一条直线上,求k的值.解:由经过两点的直线的斜率公式,得直线AB的斜率kAB与直线BC的斜率kBC相等.探究一探究二探究三易错辨析忽略直线斜率不存在的情况而致误
【典例】 设直线l过点A(7,12),B(m,13),求直线l的斜率k,并说明倾斜角α的取值范围.正解当m=7时,直线l与x轴垂直,
此时斜率不存在,倾斜角α=90°;探究一探究二探究三易错辨析纠错心得1.直线的斜率公式是在x1≠x2的条件下才成立的,当x1=x2时斜率是不存在的.因此点的坐标含有参数时,要注意参数的取值范围,若不能排除斜率不存在的情形,则需要进行分类讨论.
2.本例当m=7时,斜率不存在,不能用斜率公式,错解中漏掉了这种情况.探究一探究二探究三易错辨析变式训练若直线l的斜率k≤1,求倾斜角α的取值范围.
解:∵tan 45°=1,∴当0≤k≤1时,0°≤α≤45°;
当k<0时,90°<α<180°.
∴当k≤1时,倾斜角α的取值范围是0°≤α≤45°或90°<α<180°.1234561.已知点A(2,m),B(3,3),直线AB的斜率为1,则m的值为( )
A.1 B.2 C.3 D.4
答案:B1234562.已知A(a,2),B(3,b+1),且直线AB的倾斜角为90°,则a,b应满足( )
A.a=3,b=1 B.a=2,b=2
C.a=2,b=3 D.a=3,b∈R,且b≠1
解析:直线AB的倾斜角为90°,则斜率不存在,所以a=3,b∈R,但当b=1时,A,B两点重合,应舍去.
答案:D1234563.如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则 ( )
A.k1C.k3解析:由题图可知直线l1的倾斜角为钝角,所以k1<0;直线l2与直线l3的倾斜角为锐角,且直线l2的倾斜角较大,所以k2>k3>0,所以k2>k3>k1.
答案:D1234564.过原点,且斜率为 的直线l,绕原点按逆时针方向旋转30°到达直线l',则直线l'的斜率为 .?1234565.已知A(0,-k),B(2,3),C(2k,-1)三点共线,则实数k等于 .? 解得k=-1.
答案:-11234566.已知直线l经过点P(1,2)和Q(x,0).
(1)若直线l的倾斜角为45°,求x的值;
(2)若直线l的倾斜角为钝角,求x的取值范围.
在平面直角坐标系中,确定直线位置的几何条件是:已知直线上的一个点和这条直线的方向2.直线的倾斜角 解析:因为△AOB为等腰直角三角形,所以∠AOB=∠ABO=45°,
因此,直线OA的倾斜角为45°,直线AB的倾斜角为180°-45°=135°,又直线OB与x轴重合,所以其倾斜角为0°答案:45°,0°,135° 【做一做1】如图,已知△AOB为等腰直角三角形,则直线OA,OB,AB的倾斜角分别为 .?3.直线的斜率 4.过两点的直线斜率的计算公式
经过不同的两点P1(x1,y1),P2(x2,y2)的直线的斜率公式是【做一做2】 已知点A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率.解:因为A,B,C三点的横坐标均不相等, 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)直线的倾斜角α的取值范围是[0°,180°]. ( )
(2)直线的倾斜角越大,其斜率也越大. ( )
(3)直线的斜率越大,其倾斜角也越大. ( )
(4)若直线的斜率k=tan θ,则θ一定为该直线的倾斜角. ( )× × × × 探究一探究二探究三易错辨析探究一直线的斜率
【例1】 (1)已知一条直线的倾斜角为60°,求这条直线的斜率;
(2)求经过两点A(2,3),B(m,4)的直线的斜率.
分析:(1)利用斜率的定义求解;(2)对参数m进行分类讨论,分情况求解.探究一探究二探究三易错辨析反思感悟直线斜率的求法
1.求直线的斜率通常有两种方法:一是已知直线的倾斜角α(α≠90°)时,可利用斜率的定义,即k=tan α求得;二是已知直线所经过的两点的坐标时,可利用过两点的直线的斜率公式计算求得.
2.使用斜率公式k= 求斜率时,要注意其前提条件是x1≠x2.若x1=x2,即两点的横坐标相等时,直线的斜率不存在.
3.若两点的横坐标中含有参数,则应先讨论横坐标是否相等,再确定直线的斜率.探究一探究二探究三易错辨析变式训练1若点A(4,2),B(5,b)的连线与点C(1,2),D(3,4)的连线的斜率相等,则b的值为 .?答案:3 探究一探究二探究三易错辨析探究二直线的斜率与倾斜角的简单应用? 【例2】 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.分析:数形结合,利用斜率公式. (1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
(2)由题意可知,直线l的倾斜角在直线PB与PA的倾斜角之间.因为PB的倾斜角是45°,PA的倾斜角是135°,所以α的取值范围是45°≤α≤135°.探究一探究二探究三易错辨析反思感悟1.已知直线的倾斜角的取值范围求斜率的取值范围时,要注意对倾斜角按锐角和钝角两种情况分别进行分析求解;已知斜率的取值范围求倾斜角的取值范围时,应对斜率分正值和负值两种情况分别进行分析求解.探究一探究二探究三易错辨析变式训练2(1)当a为何值时,过点A(2a,3),B(2,-1)的直线的倾斜角是锐角、钝角或直角?
(2)若直线l的斜率k=1,求直线的倾斜角.解:(1)当过点A,B的直线的倾斜角是锐角时,kAB>0, 当倾斜角为直角时,A,B两点的横坐标相等.
即2a=2,所以a=1.
(2)设直线l的倾斜角为α,若k=1,则tan α=1.
又tan 45°=1,且0°<α<180°,所以α=45°.
所以直线的倾斜角为45°.探究一探究二探究三易错辨析探究三利用斜率解决三点共线问题? 反思感悟利用斜率证明三点共线问题的方法步骤: 【例3】 已知三点A(1,-1),B(3,3),C(4,5),求证:A,B,C三点在同一条直线上.又直线AB和BC有公共点B,
所以A,B,C三点共线.探究一探究二探究三易错辨析变式训练3若点A(2,-3),B(4,3),C(5,k)在同一条直线上,求k的值.解:由经过两点的直线的斜率公式,得直线AB的斜率kAB与直线BC的斜率kBC相等.探究一探究二探究三易错辨析忽略直线斜率不存在的情况而致误
【典例】 设直线l过点A(7,12),B(m,13),求直线l的斜率k,并说明倾斜角α的取值范围.正解当m=7时,直线l与x轴垂直,
此时斜率不存在,倾斜角α=90°;探究一探究二探究三易错辨析纠错心得1.直线的斜率公式是在x1≠x2的条件下才成立的,当x1=x2时斜率是不存在的.因此点的坐标含有参数时,要注意参数的取值范围,若不能排除斜率不存在的情形,则需要进行分类讨论.
2.本例当m=7时,斜率不存在,不能用斜率公式,错解中漏掉了这种情况.探究一探究二探究三易错辨析变式训练若直线l的斜率k≤1,求倾斜角α的取值范围.
解:∵tan 45°=1,∴当0≤k≤1时,0°≤α≤45°;
当k<0时,90°<α<180°.
∴当k≤1时,倾斜角α的取值范围是0°≤α≤45°或90°<α<180°.1234561.已知点A(2,m),B(3,3),直线AB的斜率为1,则m的值为( )
A.1 B.2 C.3 D.4
答案:B1234562.已知A(a,2),B(3,b+1),且直线AB的倾斜角为90°,则a,b应满足( )
A.a=3,b=1 B.a=2,b=2
C.a=2,b=3 D.a=3,b∈R,且b≠1
解析:直线AB的倾斜角为90°,则斜率不存在,所以a=3,b∈R,但当b=1时,A,B两点重合,应舍去.
答案:D1234563.如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则 ( )
A.k1
答案:D1234564.过原点,且斜率为 的直线l,绕原点按逆时针方向旋转30°到达直线l',则直线l'的斜率为 .?1234565.已知A(0,-k),B(2,3),C(2k,-1)三点共线,则实数k等于 .? 解得k=-1.
答案:-11234566.已知直线l经过点P(1,2)和Q(x,0).
(1)若直线l的倾斜角为45°,求x的值;
(2)若直线l的倾斜角为钝角,求x的取值范围.
