2019-2020学年高中数学北师大版必修2课件:第二章解析几何初步2.1.2.2直线方程的两点式和一般式(24张))
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第二章解析几何初步2.1.2.2直线方程的两点式和一般式(24张)) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览








文档简介
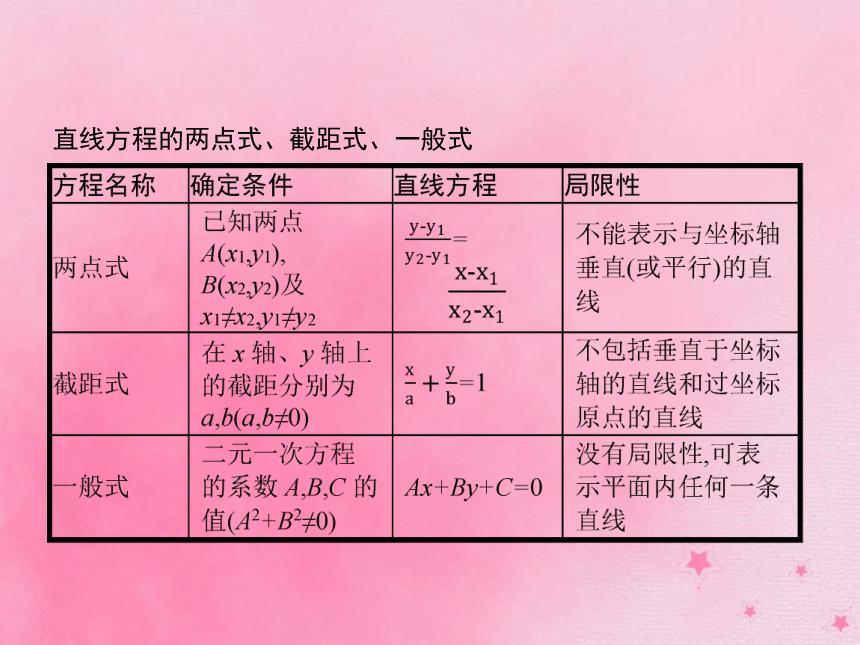
课件24张PPT。第2课时 直线方程的两点式和一般式直线方程的两点式、截距式、一般式 答案:C A.|b| B.-b2 C.b2 D.±b
答案:B归纳总结直线方程的几种形式之间的相互转化: 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)直线的一般式方程可表示任意一条直线. ( )
(2)直线的截距式可表示除过原点外的所有直线. ( )
(3)直线的两点式适用于求与两坐标轴不垂直的直线方程. ( )
(4)任何一条直线的一般式方程均能与其他四种形式(点斜式、两点式、斜截式、截距式)相互互化. ( )√ × √ × 探究一探究二探究三易错辨析探究一直线方程的两点式
【例1】 求满足下列条件的直线的方程:
(1)经过点P(2,-2),Q(3,-2);
(2)经过点C(-2,-3),D(-5,-6).
分析:先判断能否使用方程的两点式表示,若能,则写出方程的两点式;若不能,可根据点的坐标特点直接写出直线方程.解:(1)由已知得该直线垂直于y轴,故直线方程为y=-2. 整理得x-y-1=0,即所求直线方程为x-y-1=0. 探究一探究二探究三易错辨析反思感悟1.当已知两点坐标,求过这两点的直线方程时,首先要判断是否满足两点式方程的适用条件:两点的连线不垂直于坐标轴.若满足,则考虑用两点式求方程;若不满足,则可直接写出直线方程.
2.注意:由于减法的顺序性,一般用两点式求直线方程时常会将字母或数字的顺序错位而导致错误,在记忆和使用两点式方程时,必须注意坐标的对应关系,即x2与y2是同一点的坐标,而x1与y1是另一点的坐标.探究一探究二探究三易错辨析变式训练1(1)求经过点M(3,-1),N(3,2)的直线方程;
(2)求过点(-1,1)和(3,9)的直线在x轴上的截距.解:(1)由已知得,该直线垂直于x轴,故直线方程为x=3.探究一探究二探究三易错辨析直线方程的截距式
【例2】 求满足下列条件的直线方程:
(1)经过点A(0,-3)和B(4,0);
(2)经过点M(2,6),且在x轴、y轴上的截距相等.
分析对于(1)可直接由截距式写出方程,对于(2)应进行分类讨论.探究一探究二探究三易错辨析解:(1)由于直线经过点A(0,-3)和B(4,0),所以直线在x轴、y轴上的截距分别是4和-3,当直线在x轴、y轴上的截距相等,且均等于0时,设其方程为y=kx,又直线经过点M(2,6),所以6=2k,解得k=3,所以直线方程为y=3x.
综上所述,直线方程为x+y-8=0或y=3x.探究一探究二探究三易错辨析反思感悟1.当已知直线在x轴、y轴上的截距(存在且均不为0)时,可直接由截距式写出直线方程.
2.由于直线的截距式方程不能表示与坐标轴垂直和过坐标原点的直线,所以在利用待定系数法设直线的截距式方程求解时,要注意这一局限性,避免造成丢解.一般地,当直线在x轴、y轴上的截距相等、在x轴、y轴上的截距互为相反数、在x轴上的截距是在y轴上截距的k(k≠0)倍时,经过原点的直线均符合这些要求,求其方程时应分类讨论.
3.本例(2)在求解中注意不能漏掉直线y=3x,此时直线经过坐标原点,在x轴、y轴上的截距均为0,满足截距相等的条件,但不能用方程的截距式表示.探究一探究二探究三易错辨析变式训练2
如图,△ABC的三个顶点分别为A(-5,0),B(3,-3),C(0,2),求边AB和边AC所在直线的方程.解:因为直线AB经过A(-5,0),B(3,-3)两点, 整理得3x+8y+15=0,
所以直线AB的方程为3x+8y+15=0.
因为直线AC过A(-5,0),C(0,2)两点,所以由截距式得 =1,整理得2x-5y+10=0,所以直线AC的方程为2x-5y+10=0.探究一探究二探究三易错辨析直线方程的综合应用
【例3】 已知直线l的方程为(2m2+m-3)x+(m2-m)y-4m+1=0.
(1)当m为何值时,直线l的倾斜角为45°?
(2)当m为何值时,直线l在x轴上的截距为1?
(3)当m为何值时,直线l与x轴平行?
解:因为方程(2m2+m-3)x+(m2-m)y-4m+1=0表示直线,所以2m2+m-3与m2-m不能同时为0,所以m≠1.
(1)若直线l的倾斜角为45°,则其斜率为1,解得m=-1.
即当m=-1时,直线l的倾斜角为45°.探究一探究二探究三易错辨析(2)直线l在x轴上的截距为1,即直线l经过点(1,0),把点(1,0)代入直线方程,得2m2+m-3-4m+1=0,解得m=2或m=- .
即当m=2或m=- 时,直线l在x轴上的截距为1.
(3)若直线l与x轴平行,则其斜率k=0,且在y轴上的截距不为0,探究一探究二探究三易错辨析反思感悟1.对于直线Ax+By+C=0,当B≠0时,直线的斜率存在,且k=- ,这时直线方程可化为点斜式或斜截式;当B=0时,直线的斜率不存在,这时方程不能化成点斜式或斜截式.
2.一般式揭示了平面直角坐标系中直线与方程Ax+By+C=0(A2+B2≠0)的内在联系.探究一探究二探究三易错辨析变式训练3已知两条直线的方程分别为l1:x+ay+b=0,l2:x+cy+d=0,它们在坐标系中的位置如图所示,则( )
A.b>0,d<0,aB.b>0,d<0,a>c
C.b<0,d>0,a>c
D.b<0,d>0,a【典例】 求过点A(4,2),且在两坐标轴上的截距相等的直线l的方程.
错解∵直线在两坐标轴上的截距相等,探究一探究二探究三易错辨析正解:当直线的截距不为零时,由错解可得直线方程为x+y-6=0.
当直线过原点时,在两坐标轴上的截距均为零,也满足题意.
此时直线过(0,0),(4,2)两点,由两点式可得方程即x-2y=0.
综上所述,直线方程为x+y-6=0或x-2y=0. 纠错心得1.截距式方程除要求截距存在外,截距还不能为零,而在两坐标轴上的截距均为零也是本题成立的情况之一,若设斜截式方程,则可避免漏解.
2.本题错误的根源在于忽略了截距式方程的应用范围,属于思维不严密造成漏解.探究一探究二探究三易错辨析变式训练求过点A(5,2),且在两坐标轴上的截距互为相反数的直线l的方程.②当直线l不过原点时,因为直线l在两坐标轴上的截距互为相反数,即x-y-3=0.
综上所述,直线l的方程为x-y-3=0或2x-5y=0.12341.经过点A(-3,2),B(4,4)的直线的两点式方程为( ) 答案:A 12342.在x轴、y轴上的截距分别是5,-3的直线的截距式方程为( )答案:B 12343.若直线2x+3y+m=0经过第一、二、四象限,则m的取值范围是 .?答案:m<0 12344.已知△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0),AC的中点为D.
求:(1)边AC所在直线的方程;
(2)BD所在直线的方程.x-2y+8=0.
所以边AC所在直线的方程为x-2y+8=0.
(2)由题意知,点D的坐标为(-4,2),则由直线的两点式方程得BD所故BD所在直线的方程为2x-y+10=0.
答案:B归纳总结直线方程的几种形式之间的相互转化: 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)直线的一般式方程可表示任意一条直线. ( )
(2)直线的截距式可表示除过原点外的所有直线. ( )
(3)直线的两点式适用于求与两坐标轴不垂直的直线方程. ( )
(4)任何一条直线的一般式方程均能与其他四种形式(点斜式、两点式、斜截式、截距式)相互互化. ( )√ × √ × 探究一探究二探究三易错辨析探究一直线方程的两点式
【例1】 求满足下列条件的直线的方程:
(1)经过点P(2,-2),Q(3,-2);
(2)经过点C(-2,-3),D(-5,-6).
分析:先判断能否使用方程的两点式表示,若能,则写出方程的两点式;若不能,可根据点的坐标特点直接写出直线方程.解:(1)由已知得该直线垂直于y轴,故直线方程为y=-2. 整理得x-y-1=0,即所求直线方程为x-y-1=0. 探究一探究二探究三易错辨析反思感悟1.当已知两点坐标,求过这两点的直线方程时,首先要判断是否满足两点式方程的适用条件:两点的连线不垂直于坐标轴.若满足,则考虑用两点式求方程;若不满足,则可直接写出直线方程.
2.注意:由于减法的顺序性,一般用两点式求直线方程时常会将字母或数字的顺序错位而导致错误,在记忆和使用两点式方程时,必须注意坐标的对应关系,即x2与y2是同一点的坐标,而x1与y1是另一点的坐标.探究一探究二探究三易错辨析变式训练1(1)求经过点M(3,-1),N(3,2)的直线方程;
(2)求过点(-1,1)和(3,9)的直线在x轴上的截距.解:(1)由已知得,该直线垂直于x轴,故直线方程为x=3.探究一探究二探究三易错辨析直线方程的截距式
【例2】 求满足下列条件的直线方程:
(1)经过点A(0,-3)和B(4,0);
(2)经过点M(2,6),且在x轴、y轴上的截距相等.
分析对于(1)可直接由截距式写出方程,对于(2)应进行分类讨论.探究一探究二探究三易错辨析解:(1)由于直线经过点A(0,-3)和B(4,0),所以直线在x轴、y轴上的截距分别是4和-3,当直线在x轴、y轴上的截距相等,且均等于0时,设其方程为y=kx,又直线经过点M(2,6),所以6=2k,解得k=3,所以直线方程为y=3x.
综上所述,直线方程为x+y-8=0或y=3x.探究一探究二探究三易错辨析反思感悟1.当已知直线在x轴、y轴上的截距(存在且均不为0)时,可直接由截距式写出直线方程.
2.由于直线的截距式方程不能表示与坐标轴垂直和过坐标原点的直线,所以在利用待定系数法设直线的截距式方程求解时,要注意这一局限性,避免造成丢解.一般地,当直线在x轴、y轴上的截距相等、在x轴、y轴上的截距互为相反数、在x轴上的截距是在y轴上截距的k(k≠0)倍时,经过原点的直线均符合这些要求,求其方程时应分类讨论.
3.本例(2)在求解中注意不能漏掉直线y=3x,此时直线经过坐标原点,在x轴、y轴上的截距均为0,满足截距相等的条件,但不能用方程的截距式表示.探究一探究二探究三易错辨析变式训练2
如图,△ABC的三个顶点分别为A(-5,0),B(3,-3),C(0,2),求边AB和边AC所在直线的方程.解:因为直线AB经过A(-5,0),B(3,-3)两点, 整理得3x+8y+15=0,
所以直线AB的方程为3x+8y+15=0.
因为直线AC过A(-5,0),C(0,2)两点,所以由截距式得 =1,整理得2x-5y+10=0,所以直线AC的方程为2x-5y+10=0.探究一探究二探究三易错辨析直线方程的综合应用
【例3】 已知直线l的方程为(2m2+m-3)x+(m2-m)y-4m+1=0.
(1)当m为何值时,直线l的倾斜角为45°?
(2)当m为何值时,直线l在x轴上的截距为1?
(3)当m为何值时,直线l与x轴平行?
解:因为方程(2m2+m-3)x+(m2-m)y-4m+1=0表示直线,所以2m2+m-3与m2-m不能同时为0,所以m≠1.
(1)若直线l的倾斜角为45°,则其斜率为1,解得m=-1.
即当m=-1时,直线l的倾斜角为45°.探究一探究二探究三易错辨析(2)直线l在x轴上的截距为1,即直线l经过点(1,0),把点(1,0)代入直线方程,得2m2+m-3-4m+1=0,解得m=2或m=- .
即当m=2或m=- 时,直线l在x轴上的截距为1.
(3)若直线l与x轴平行,则其斜率k=0,且在y轴上的截距不为0,探究一探究二探究三易错辨析反思感悟1.对于直线Ax+By+C=0,当B≠0时,直线的斜率存在,且k=- ,这时直线方程可化为点斜式或斜截式;当B=0时,直线的斜率不存在,这时方程不能化成点斜式或斜截式.
2.一般式揭示了平面直角坐标系中直线与方程Ax+By+C=0(A2+B2≠0)的内在联系.探究一探究二探究三易错辨析变式训练3已知两条直线的方程分别为l1:x+ay+b=0,l2:x+cy+d=0,它们在坐标系中的位置如图所示,则( )
A.b>0,d<0,a
C.b<0,d>0,a>c
D.b<0,d>0,a
错解∵直线在两坐标轴上的截距相等,探究一探究二探究三易错辨析正解:当直线的截距不为零时,由错解可得直线方程为x+y-6=0.
当直线过原点时,在两坐标轴上的截距均为零,也满足题意.
此时直线过(0,0),(4,2)两点,由两点式可得方程即x-2y=0.
综上所述,直线方程为x+y-6=0或x-2y=0. 纠错心得1.截距式方程除要求截距存在外,截距还不能为零,而在两坐标轴上的截距均为零也是本题成立的情况之一,若设斜截式方程,则可避免漏解.
2.本题错误的根源在于忽略了截距式方程的应用范围,属于思维不严密造成漏解.探究一探究二探究三易错辨析变式训练求过点A(5,2),且在两坐标轴上的截距互为相反数的直线l的方程.②当直线l不过原点时,因为直线l在两坐标轴上的截距互为相反数,即x-y-3=0.
综上所述,直线l的方程为x-y-3=0或2x-5y=0.12341.经过点A(-3,2),B(4,4)的直线的两点式方程为( ) 答案:A 12342.在x轴、y轴上的截距分别是5,-3的直线的截距式方程为( )答案:B 12343.若直线2x+3y+m=0经过第一、二、四象限,则m的取值范围是 .?答案:m<0 12344.已知△ABC的三个顶点分别为A(0,4),B(-2,6),C(-8,0),AC的中点为D.
求:(1)边AC所在直线的方程;
(2)BD所在直线的方程.x-2y+8=0.
所以边AC所在直线的方程为x-2y+8=0.
(2)由题意知,点D的坐标为(-4,2),则由直线的两点式方程得BD所故BD所在直线的方程为2x-y+10=0.
