2019-2020学年高中数学北师大版必修2课件:第二章解析几何初步2.2.3.2圆与圆的位置关系(29张)
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第二章解析几何初步2.2.3.2圆与圆的位置关系(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览








文档简介
课件29张PPT。第2课时 圆与圆的位置关系1.圆与圆的位置关系
圆与圆的位置关系有五种,分别为相离、外切、相交、内切、内含.
2.圆与圆的位置关系的判断
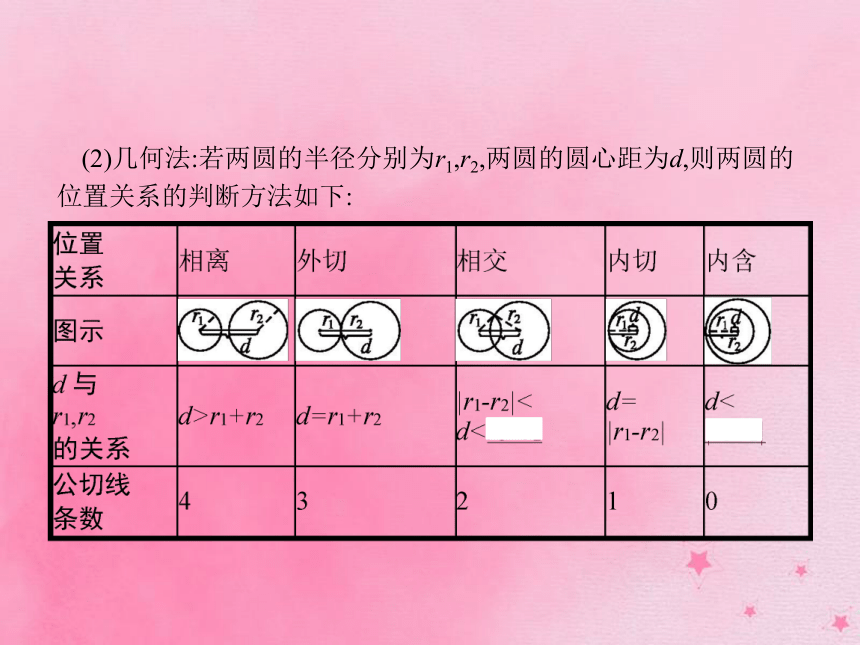
(1)代数法:设两圆方程分别为则方程组解的个数与两圆的位置关系如下: (2)几何法:若两圆的半径分别为r1,r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下:【做一做1】 圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( )
A.内切 B.相交
C.外切 D.相离
解析:两圆圆心分别为O1(-2,0),O2(2,1),半径分别为r1=2,r2=3.答案:B 【做一做2】 若圆x2+y2=9与圆(x-4)2+(y+3)2=r有3条公切线,则实数r的值为( )
A.8 B.64 C.2 D.4
解析:两圆有3条公切线,即两圆外切,答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若两圆只有一个公共点,则这两圆外切. ( )
(2)若两圆无公共点,则两圆相离. ( )
(3)两个半径不相等的同心圆从两圆位置关系上来说为内含. ( )
(4)过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1,且λ∈R),此圆系方程涵盖了过圆C1与圆C2的交点的所有圆的方程. ( )× × √ × 探究一探究二探究三易错辨析探究一判断两圆的位置关系
【例1】 已知圆C1:x2+y2-2mx+4y+m2-5=0与圆C2:x2+y2+2x=0.
(1)当m=1时,圆C1与圆C2是什么关系?
(2)若两圆有三条公切线,求实数m的值.
(3)是否存在m使得圆C1与圆C2内含?
分析:(1)参数m的值已知,求解时可先找出圆心及半径,然后比较两圆的圆心距d与r1+r2,|r1-r2|的大小关系.(2)两圆有三条公切线即两圆相外切,由此建立关于m的等式求解.(3)假设存在m使得圆C1与圆C2内含,则圆心距d<|r1-r2|.探究一探究二探究三易错辨析解:(1)∵m=1,∴两圆的方程分别可化为C1:(x-1)2+(y+2)2=9,C2:(x+1)2+y2=1.又r1+r2=3+1=4,|r1-r2|=|3-1|=2,
∴|r1-r2|∴圆C1与圆C2相交.
(2)圆C1的方程为(x-m)2+(y+2)2=9,∴圆心C1(m,-2),半径r1=3,圆C2的方程为(x+1)2+y2=1,
∴圆心C2(-1,0),半径r2=1,
当两圆有三条公切线时,它们相外切,因此|C1C2|=r1+r2,探究一探究二探究三易错辨析(3)假设存在m使得圆C1与圆C2内含, 故不存在m使得圆C1与圆C2内含. 反思感悟判断两圆的位置关系,通常采用几何法,而不是用两圆公共点的个数来判断,因为它们之间并不是一一对应关系,如两圆只有一个公共点时,两圆可能内切,也可能外切;两圆没有公共点时,它们可能相离,也可能内含,无法确定是哪一种位置关系.探究一探究二探究三易错辨析变式训练1(1)若圆C1:x2+y2-2mx+m2=4与圆C2:x2+y2+2x=8外切,则m的值为( )
A.-6 B.4 C.-6或4 D.不存在
(2)若圆B:x2+y2+b=0与圆C:x2+y2-6x+8y=0没有公共点,则b的取值范围是 .?
解析:(1)将两圆的方程整理得圆C1:(x-m)2+y2=4,圆C2:(x+1)2+y2=9,所以两圆的圆心坐标分别为(m,0),(-1,0),半径分别为2,3.由已知得|m+1|=2+3,解得m=-6或m=4.
(2)由已知圆C:(x-3)2+(y+4)2=25,圆B:x2+y2=-b,
∵-b>0,∴b<0.
∵圆B的圆心恰在圆C上,要想两圆无公共点,答案:(1)C (2)b<-100 探究一探究二探究三易错辨析【例2】 已知圆O:x2+y2=25和圆C:x2+y2-4x-2y-20=0相交于A,B两点.
(1)求线段AB的垂直平分线的方程;
(2)求AB所在直线的方程;
(3)求公共弦AB的长度.
分析:(1)线段AB的垂直平分线即两圆圆心的连线;(2)两圆方程相减即得AB所在直线的方程;(3)利用几何法根据勾股定理求AB的长.探究二两圆的公共弦问题 探究一探究二探究三易错辨析解:(1)因为两圆相交于A,B两点,所以线段AB的垂直平分线就是两圆的圆心的连线.
又圆O:x2+y2=25的圆心O(0,0),圆C:(x-2)2+(y-1)2=25的圆心C(2,1),
所以kOC= ,由点斜式得y= x,即x-2y=0.故AB的垂直平分线的方程为x-2y=0.
(2)将两圆方程相减即得公共弦AB所在直线的方程为4x+2y-5=0.探究一探究二探究三易错辨析反思感悟1.两圆相交时,公共弦所在的直线方程的求法
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在直线的方程为(D1-D2)x+(E1-E2)y+F1-F2=0,即两圆方程相减可得公共弦所在的直线方程.
2.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
3.(1)当两圆内切时,两圆方程相减所得直线方程即为两圆的公切线方程;当两圆外切时,两圆方程相减所得直线方程为两圆的内公切线的方程.
(2)当两圆相离时,两圆方程相减也能得一条直线方程,但这条直线方程不是两圆的公共弦所在的直线方程.探究一探究二探究三易错辨析变式训练2已知圆C1:x2+y2+2x+2y-8=0与圆C2:x2+y2-2x+10y-24=0相交于A,B两点.
(1)求公共弦AB所在直线的方程;
(2)求圆心在直线y=-x上,且经过A,B两点的圆的方程.①-②并整理得公共弦AB所在直线的方程为x-2y+4=0. 探究一探究二探究三易错辨析(2)由(1)得x=2y-4,将其代入x2+y2+2x+2y-8=0中并整理得y2-2y=0,∵圆心在直线y=-x上,
∴设圆心为M(x,-x).
则|MA|=|MB|,解得x=-3,即M(-3,3). ∴圆M的方程为(x+3)2+(y-3)2=10. 探究一探究二探究三易错辨析探究三与两圆相切有关的问题? 【例3】已知点F(0,1),一动圆过点F且与圆x2+(y+1)2=8内切,求动圆圆心的轨迹方程. 分析:解答本题的关键是通过内切建立等量关系,解题时应注意半径间的关系.探究一探究二探究三易错辨析反思感悟涉及与圆相关的轨迹求法:
(1)建立适当的坐标系;
(2)利用圆与圆的位置关系建立等量关系;
(3)对上述等量关系进行化简;
(4)明确曲线形式,并验证范围的有效性.探究一探究二探究三易错辨析变式训练3若圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称,过点C(-a,a)的圆P与y轴相切,则圆心P的轨迹方程为( )
A.y2-4x+4y+8=0
B.y2+2x-2y+2=0
C.y2+4x-4y+8=0
D.y2-2x-y-1=0
解析:由圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称可知两圆半径相等且两圆圆心连线的中点在直线y=x-1上.故可得a=2,即点C(-2,2),所以过点C(-2,2)且与y轴相切的圆P的圆心的轨迹方程为(x+2)2+(y-2)2=x2,整理得y2+4x-4y+8=0.
答案:C探究一探究二探究三易错辨析忽略了两圆内切的情况而致误
【典例】 求半径为4,与圆A:x2+y2-4x-2y-4=0相切,且和直线y=0相切的圆C的方程.
错解由题意知所求的圆与直线y=0相切,且半径为4,
设其圆心C的坐标为(a,4),
则其方程为(x-a)2+(y-4)2=42.
圆A的方程可整理为(x-2)2+(y-1)2=32,
所以其圆心为A(2,1),半径为3.
由两圆相切得|CA|=3+4=7,探究一探究二探究三易错辨析正解:由题意设所求圆的方程为(x-a)2+(y-b)2=r2,圆心为C.
因为圆C与直线y=0相切且半径为4,
所以圆心C的坐标为(a,4)或(a,-4).
依题可知圆A:x2+y2-4x-2y-4=0的圆心A的坐标为(2,1),半径为3.
若两圆相切,则|CA|=4+3=7或|CA|=4-3=1.
当圆心C的坐标为C(a,4)时,当圆心C的坐标为(a,-4)时, 探究一探究二探究三易错辨析纠错心得1.当圆和直线y=0相切时,圆心可能在直线y=0的上方,也可能在直线y=0的下方,圆与圆相切有外切和内切两种情况,考虑问题应全面.
2.错解只考虑了圆心在直线y=0上方的情形,同时只考虑了两圆外切的情况.1234561.圆C1:(x-1)2+(y-2)2=4与圆C2:(x+2)2+(y+2)2=9的位置关系是( )
A.相离 B.外切 C.相交 D.内切则d=r1+r2,即两圆外切.
答案:B1234562.已知圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则公共弦AB的垂直平分线的方程为( )
A.x+y+3=0 B.2x-y-5=0
C.3x-y-9=0 D.4x-3y+7=0
解析:由题意知,公共弦AB的垂直平分线即为两圆圆心连线所在直线.
两圆的圆心分别为(2,-3),(3,0).直线方程为3x-y-9=0.
答案:C1234563.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )
A.(x-4)2+(y-6)2=6
B.(x±4)2+(y-6)2=6
C.(x-4)2+(y-6)2=36
D.(x±4)2+(y-6)2=36
解析:由题意知,设所求圆的方程为(x-a)2+(y-6)2=36,
又与圆x2+(y-3)2=1内切,∴a2=16.∴a=±4.∴选D.
答案:D1234564.过两圆C1:(x-4)2+(y-5)2=10,C2:(x+2)2+(y-7)2=12的交点的直线方程为 .?
解析:将两圆方程化为一般式并联立得两式相减得12x-4y+10=0,即6x-2y+5=0.
答案:6x-2y+5=01234565.以(4,-3)为圆心,且与圆x2+y2=1外切的圆的方程为 .?得r=4.
故所求圆的方程为(x-4)2+(y+3)2=16.
答案:(x-4)2+(y+3)2=166.如图,圆O1与圆O2的半径都等于1,|O1O2|=4,过动点P分别作圆O1、圆O2的切线PM,PN(M,N为切点),使得|PM|= |PN|.建立适当的平面直角坐标系,并求动点P的轨迹方程.123456123456解:以O1O2的中点O为原点,O1O2所在直线为x轴,O1O2的中垂线为y轴,建立如图所示的平面直角坐标系.
则O1(-2,0),O2(2,0).
又因为两圆的半径均为1,
所以|PO1|2-1=2(|PO2|2-1).
设点P为(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],
即(x-6)2+y2=33,故所求动点P的轨迹方程为x2+y2-12x+3=0.
圆与圆的位置关系有五种,分别为相离、外切、相交、内切、内含.
2.圆与圆的位置关系的判断
(1)代数法:设两圆方程分别为则方程组解的个数与两圆的位置关系如下: (2)几何法:若两圆的半径分别为r1,r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下:【做一做1】 圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( )
A.内切 B.相交
C.外切 D.相离
解析:两圆圆心分别为O1(-2,0),O2(2,1),半径分别为r1=2,r2=3.答案:B 【做一做2】 若圆x2+y2=9与圆(x-4)2+(y+3)2=r有3条公切线,则实数r的值为( )
A.8 B.64 C.2 D.4
解析:两圆有3条公切线,即两圆外切,答案:D 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若两圆只有一个公共点,则这两圆外切. ( )
(2)若两圆无公共点,则两圆相离. ( )
(3)两个半径不相等的同心圆从两圆位置关系上来说为内含. ( )
(4)过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1,且λ∈R),此圆系方程涵盖了过圆C1与圆C2的交点的所有圆的方程. ( )× × √ × 探究一探究二探究三易错辨析探究一判断两圆的位置关系
【例1】 已知圆C1:x2+y2-2mx+4y+m2-5=0与圆C2:x2+y2+2x=0.
(1)当m=1时,圆C1与圆C2是什么关系?
(2)若两圆有三条公切线,求实数m的值.
(3)是否存在m使得圆C1与圆C2内含?
分析:(1)参数m的值已知,求解时可先找出圆心及半径,然后比较两圆的圆心距d与r1+r2,|r1-r2|的大小关系.(2)两圆有三条公切线即两圆相外切,由此建立关于m的等式求解.(3)假设存在m使得圆C1与圆C2内含,则圆心距d<|r1-r2|.探究一探究二探究三易错辨析解:(1)∵m=1,∴两圆的方程分别可化为C1:(x-1)2+(y+2)2=9,C2:(x+1)2+y2=1.又r1+r2=3+1=4,|r1-r2|=|3-1|=2,
∴|r1-r2|
(2)圆C1的方程为(x-m)2+(y+2)2=9,∴圆心C1(m,-2),半径r1=3,圆C2的方程为(x+1)2+y2=1,
∴圆心C2(-1,0),半径r2=1,
当两圆有三条公切线时,它们相外切,因此|C1C2|=r1+r2,探究一探究二探究三易错辨析(3)假设存在m使得圆C1与圆C2内含, 故不存在m使得圆C1与圆C2内含. 反思感悟判断两圆的位置关系,通常采用几何法,而不是用两圆公共点的个数来判断,因为它们之间并不是一一对应关系,如两圆只有一个公共点时,两圆可能内切,也可能外切;两圆没有公共点时,它们可能相离,也可能内含,无法确定是哪一种位置关系.探究一探究二探究三易错辨析变式训练1(1)若圆C1:x2+y2-2mx+m2=4与圆C2:x2+y2+2x=8外切,则m的值为( )
A.-6 B.4 C.-6或4 D.不存在
(2)若圆B:x2+y2+b=0与圆C:x2+y2-6x+8y=0没有公共点,则b的取值范围是 .?
解析:(1)将两圆的方程整理得圆C1:(x-m)2+y2=4,圆C2:(x+1)2+y2=9,所以两圆的圆心坐标分别为(m,0),(-1,0),半径分别为2,3.由已知得|m+1|=2+3,解得m=-6或m=4.
(2)由已知圆C:(x-3)2+(y+4)2=25,圆B:x2+y2=-b,
∵-b>0,∴b<0.
∵圆B的圆心恰在圆C上,要想两圆无公共点,答案:(1)C (2)b<-100 探究一探究二探究三易错辨析【例2】 已知圆O:x2+y2=25和圆C:x2+y2-4x-2y-20=0相交于A,B两点.
(1)求线段AB的垂直平分线的方程;
(2)求AB所在直线的方程;
(3)求公共弦AB的长度.
分析:(1)线段AB的垂直平分线即两圆圆心的连线;(2)两圆方程相减即得AB所在直线的方程;(3)利用几何法根据勾股定理求AB的长.探究二两圆的公共弦问题 探究一探究二探究三易错辨析解:(1)因为两圆相交于A,B两点,所以线段AB的垂直平分线就是两圆的圆心的连线.
又圆O:x2+y2=25的圆心O(0,0),圆C:(x-2)2+(y-1)2=25的圆心C(2,1),
所以kOC= ,由点斜式得y= x,即x-2y=0.故AB的垂直平分线的方程为x-2y=0.
(2)将两圆方程相减即得公共弦AB所在直线的方程为4x+2y-5=0.探究一探究二探究三易错辨析反思感悟1.两圆相交时,公共弦所在的直线方程的求法
若圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则两圆公共弦所在直线的方程为(D1-D2)x+(E1-E2)y+F1-F2=0,即两圆方程相减可得公共弦所在的直线方程.
2.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
3.(1)当两圆内切时,两圆方程相减所得直线方程即为两圆的公切线方程;当两圆外切时,两圆方程相减所得直线方程为两圆的内公切线的方程.
(2)当两圆相离时,两圆方程相减也能得一条直线方程,但这条直线方程不是两圆的公共弦所在的直线方程.探究一探究二探究三易错辨析变式训练2已知圆C1:x2+y2+2x+2y-8=0与圆C2:x2+y2-2x+10y-24=0相交于A,B两点.
(1)求公共弦AB所在直线的方程;
(2)求圆心在直线y=-x上,且经过A,B两点的圆的方程.①-②并整理得公共弦AB所在直线的方程为x-2y+4=0. 探究一探究二探究三易错辨析(2)由(1)得x=2y-4,将其代入x2+y2+2x+2y-8=0中并整理得y2-2y=0,∵圆心在直线y=-x上,
∴设圆心为M(x,-x).
则|MA|=|MB|,解得x=-3,即M(-3,3). ∴圆M的方程为(x+3)2+(y-3)2=10. 探究一探究二探究三易错辨析探究三与两圆相切有关的问题? 【例3】已知点F(0,1),一动圆过点F且与圆x2+(y+1)2=8内切,求动圆圆心的轨迹方程. 分析:解答本题的关键是通过内切建立等量关系,解题时应注意半径间的关系.探究一探究二探究三易错辨析反思感悟涉及与圆相关的轨迹求法:
(1)建立适当的坐标系;
(2)利用圆与圆的位置关系建立等量关系;
(3)对上述等量关系进行化简;
(4)明确曲线形式,并验证范围的有效性.探究一探究二探究三易错辨析变式训练3若圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称,过点C(-a,a)的圆P与y轴相切,则圆心P的轨迹方程为( )
A.y2-4x+4y+8=0
B.y2+2x-2y+2=0
C.y2+4x-4y+8=0
D.y2-2x-y-1=0
解析:由圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称可知两圆半径相等且两圆圆心连线的中点在直线y=x-1上.故可得a=2,即点C(-2,2),所以过点C(-2,2)且与y轴相切的圆P的圆心的轨迹方程为(x+2)2+(y-2)2=x2,整理得y2+4x-4y+8=0.
答案:C探究一探究二探究三易错辨析忽略了两圆内切的情况而致误
【典例】 求半径为4,与圆A:x2+y2-4x-2y-4=0相切,且和直线y=0相切的圆C的方程.
错解由题意知所求的圆与直线y=0相切,且半径为4,
设其圆心C的坐标为(a,4),
则其方程为(x-a)2+(y-4)2=42.
圆A的方程可整理为(x-2)2+(y-1)2=32,
所以其圆心为A(2,1),半径为3.
由两圆相切得|CA|=3+4=7,探究一探究二探究三易错辨析正解:由题意设所求圆的方程为(x-a)2+(y-b)2=r2,圆心为C.
因为圆C与直线y=0相切且半径为4,
所以圆心C的坐标为(a,4)或(a,-4).
依题可知圆A:x2+y2-4x-2y-4=0的圆心A的坐标为(2,1),半径为3.
若两圆相切,则|CA|=4+3=7或|CA|=4-3=1.
当圆心C的坐标为C(a,4)时,当圆心C的坐标为(a,-4)时, 探究一探究二探究三易错辨析纠错心得1.当圆和直线y=0相切时,圆心可能在直线y=0的上方,也可能在直线y=0的下方,圆与圆相切有外切和内切两种情况,考虑问题应全面.
2.错解只考虑了圆心在直线y=0上方的情形,同时只考虑了两圆外切的情况.1234561.圆C1:(x-1)2+(y-2)2=4与圆C2:(x+2)2+(y+2)2=9的位置关系是( )
A.相离 B.外切 C.相交 D.内切则d=r1+r2,即两圆外切.
答案:B1234562.已知圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则公共弦AB的垂直平分线的方程为( )
A.x+y+3=0 B.2x-y-5=0
C.3x-y-9=0 D.4x-3y+7=0
解析:由题意知,公共弦AB的垂直平分线即为两圆圆心连线所在直线.
两圆的圆心分别为(2,-3),(3,0).直线方程为3x-y-9=0.
答案:C1234563.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )
A.(x-4)2+(y-6)2=6
B.(x±4)2+(y-6)2=6
C.(x-4)2+(y-6)2=36
D.(x±4)2+(y-6)2=36
解析:由题意知,设所求圆的方程为(x-a)2+(y-6)2=36,
又与圆x2+(y-3)2=1内切,∴a2=16.∴a=±4.∴选D.
答案:D1234564.过两圆C1:(x-4)2+(y-5)2=10,C2:(x+2)2+(y-7)2=12的交点的直线方程为 .?
解析:将两圆方程化为一般式并联立得两式相减得12x-4y+10=0,即6x-2y+5=0.
答案:6x-2y+5=01234565.以(4,-3)为圆心,且与圆x2+y2=1外切的圆的方程为 .?得r=4.
故所求圆的方程为(x-4)2+(y+3)2=16.
答案:(x-4)2+(y+3)2=166.如图,圆O1与圆O2的半径都等于1,|O1O2|=4,过动点P分别作圆O1、圆O2的切线PM,PN(M,N为切点),使得|PM|= |PN|.建立适当的平面直角坐标系,并求动点P的轨迹方程.123456123456解:以O1O2的中点O为原点,O1O2所在直线为x轴,O1O2的中垂线为y轴,建立如图所示的平面直角坐标系.
则O1(-2,0),O2(2,0).
又因为两圆的半径均为1,
所以|PO1|2-1=2(|PO2|2-1).
设点P为(x,y),则(x+2)2+y2-1=2[(x-2)2+y2-1],
即(x-6)2+y2=33,故所求动点P的轨迹方程为x2+y2-12x+3=0.
