2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.1简单几何体(36张)
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.1简单几何体(36张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览







文档简介
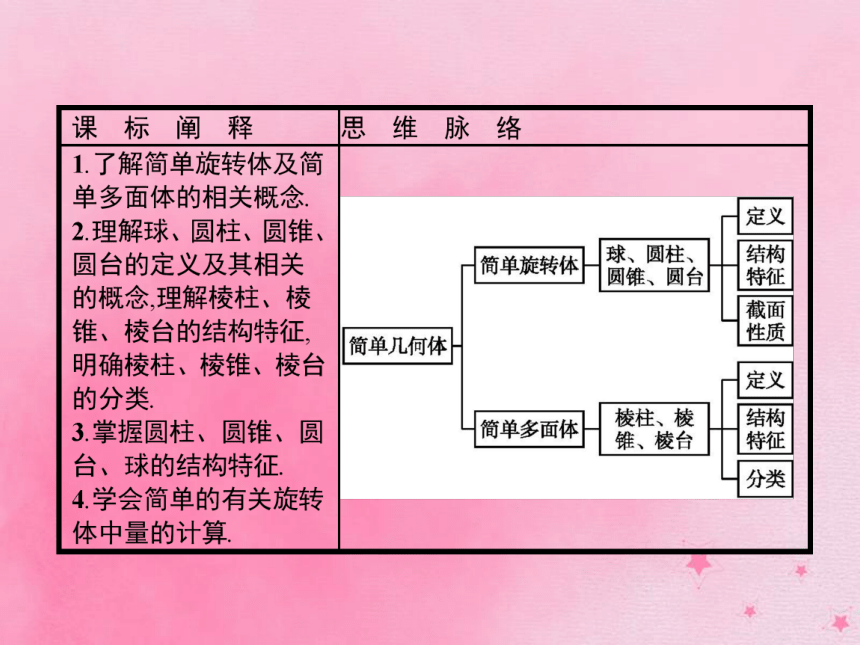
课件36张PPT。第一章 立体几何初步§1 简单几何体1.球
(1)球面:以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面.
(2)球:球面所围成的几何体叫作球体,简称球.
(3)球的有关概念:
①球心:半圆的圆心.
②球的半径:连接球心和球面上任意一点的线段.
③球的直径:连接球面上两点并且过球心的线段.2.旋转体
(1)旋转面:一条平面曲线绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面.
(2)旋转体:封闭的旋转面围成的几何体叫作旋转体.(3)圆柱、圆锥、圆台
①定义:分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作圆柱、圆锥、圆台.
②底面、侧面及侧面的母线:
底面:垂直于旋转轴的边旋转而成的圆面.
侧面:不垂直于旋转轴的边旋转而成的曲面.
侧面的母线:无论转到什么位置,不垂直于旋转轴的边.
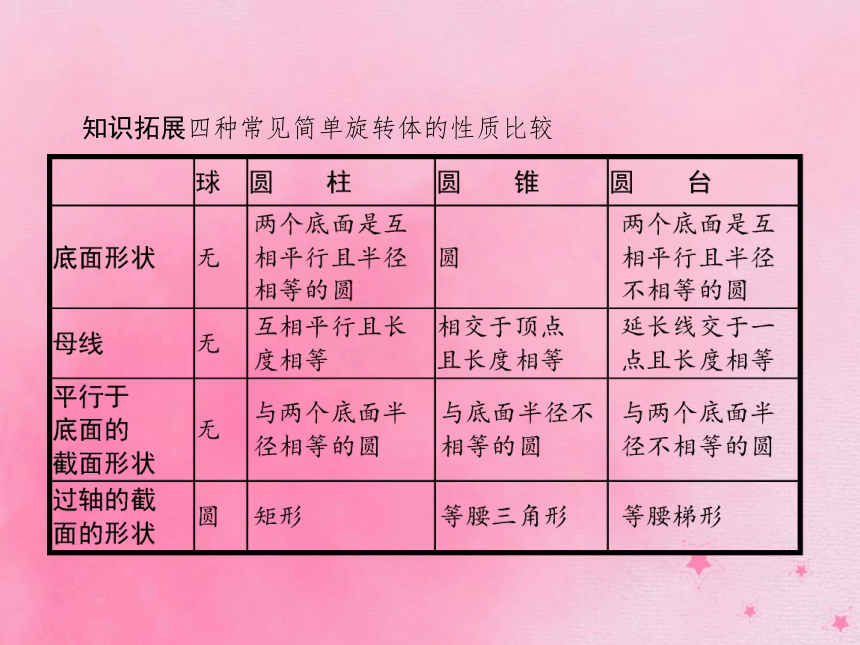
③圆台也可以看作是用平行于圆锥底面的平面截这个圆锥而得到的.知识拓展四种常见简单旋转体的性质比较 3.多面体
我们把若干个平面多边形围成的几何体叫作多面体.其中棱柱、棱锥、棱台是简单多面体.
(1)棱柱
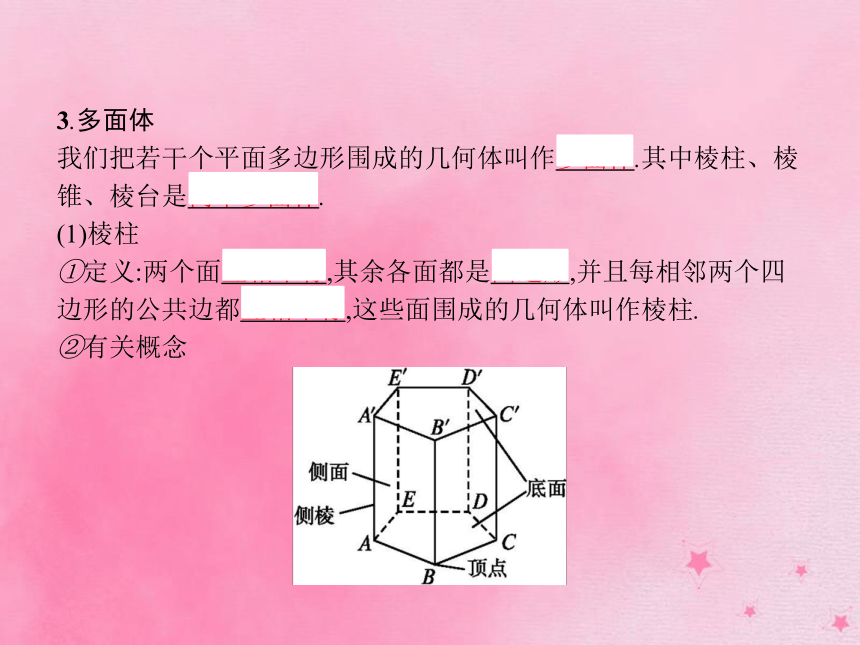
①定义:两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫作棱柱.
②有关概念③分类 正棱柱:底面是正多边形的直棱柱叫作正棱柱.
④表示:通常用底面各顶点的字母表示棱柱.如上图中的棱柱可记作:五棱柱ABCDE-A'B'C'D'E'.(2)棱锥
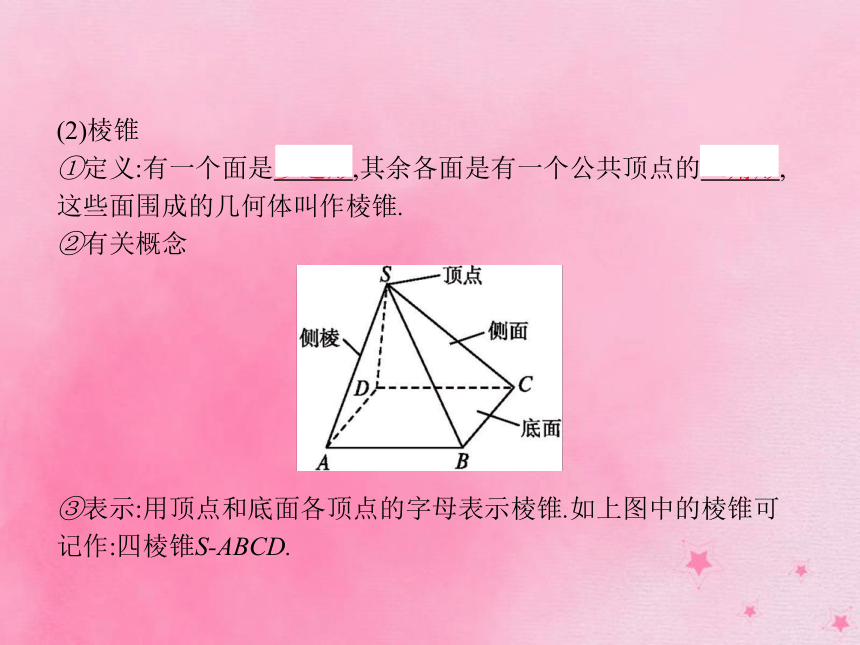
①定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.
②有关概念
③表示:用顶点和底面各顶点的字母表示棱锥.如上图中的棱锥可记作:四棱锥S-ABCD.④分类
按底面多边形的边数分为:三棱锥、四棱锥、五棱锥……,其中三棱锥也叫作四面体.(3)棱台
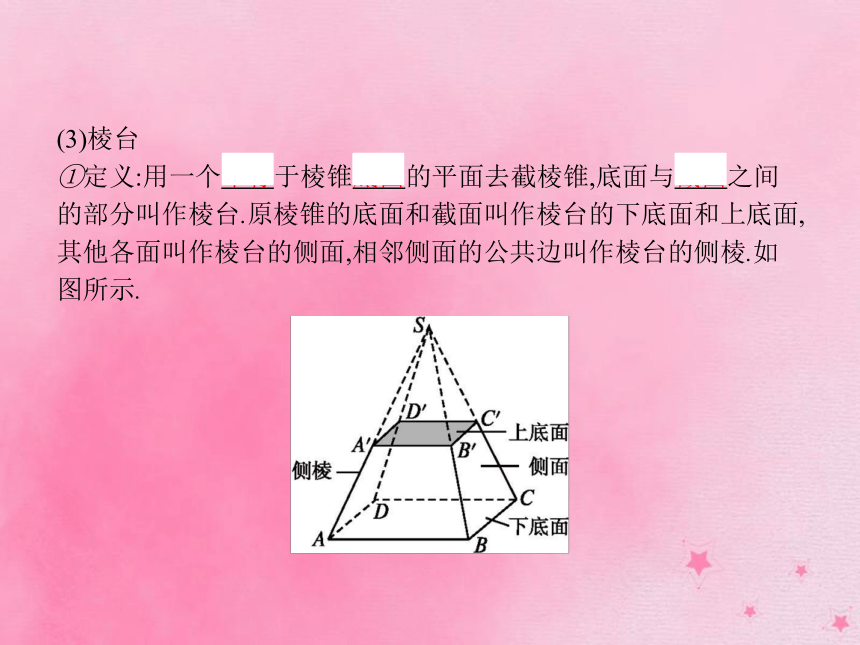
①定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.原棱锥的底面和截面叫作棱台的下底面和上底面,其他各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的侧棱.如图所示.②表示:用表示底面各顶点的字母表示棱台.如上图中的棱台可记作:四棱台ABCD-A'B'C'D'.
③分类:按底面多边形的边数分为三棱台、四棱台、五棱台……
④特殊的棱台:用正棱锥截得的棱台叫作正棱台.正棱台的侧面是全等的等腰梯形.归纳总结个棱柱、棱锥、棱台的性质比较 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)过球面上的两点可作无数个大圆. ( )
(2)连接圆柱上、下底面圆周上两点的线段是圆柱的母线. ( )
(3)圆锥截去一个小圆锥后剩余部分是圆台. ( )
(4)每个面都是三角形的几何体就是棱锥. ( )
(5)有两个面互相平行,其余各面都是平行四边形的多面体就是棱柱. ( )× × √ × × 探究一探究二探究三分析:解答本题可先根据圆柱、圆锥、圆台、球的结构特征详细分析,再结合已知的各个命题的条件进行具体分析.探究一对旋转体有关概念及其结构特征的理解
【例1】 判断下列说法是否正确,并说明理由:
(1)圆柱的任意两条母线所在的直线是平行的;
(2)用一个平面截圆锥,得到一个圆锥和一个圆台;
(3)球是以半圆的直径所在的直线为旋转轴,半圆旋转一周形成的旋转体;
(4)圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线.探究四探究一探究二探究三解:(1)正确.由圆柱母线的定义知,圆柱的任意两条母线所在的直线是平行的.
(2)错误.用平行于圆锥底面的平面去截圆锥,才能得到一个圆锥和一个圆台,用不平行于圆锥底面的平面截圆锥,则不能得到一个圆锥和一个圆台.
(3)正确.由球的定义易知该说法正确.
(4)正确.由圆锥母线的定义知,圆锥顶点与底面圆周上任意一点的连线都是母线.反思感悟1.判断旋转体类型的关键是轴的确定,看旋转体是由平面图形绕哪条直线旋转所得,同一个平面图形绕不同的轴旋转,所得的旋转体一般是不同的.
2.球、圆柱、圆锥、圆台都是旋转体,但旋转体不仅仅是这几种几何体,也可以是这几种几何体的组合体.探究四探究一探究二探究三变式训练1如图(1)(2)所示的图形绕虚线旋转一周后形成的立体图形分别是由哪些简单几何体组成的?探究四探究一探究二探究三解:旋转后的图形如图所示.其中图①是由一个圆柱O1O2和两个圆台O2O3,O3O4组成的;图②是由一个圆锥O5O4,一个圆柱O3O4及一个圆台O1O3中挖去圆锥O2O1组成的.探究四探究一探究二探究三探究二简单旋转体中有关量的计算?
【例2】一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2.求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.探究四探究一探究二探究三解:(1)设圆台的轴截面是等腰梯形ABCD,如图所示,由已知可得上底面的半径O1A=2 cm,下底面的半径OB=5 cm,腰长AB=12 cm,(2)设截得此圆台的圆锥的母线长为l cm,由△SAO1∽△SBO, 故截得此圆台的圆锥的母线长为20 cm.
反思感悟1.对于旋转体来说,轴截面既能揭示几何体各元素的数量关系,又能“化立体为平面”.
2.圆台一般都要先转化为圆锥,再进行计算或求值.探究四探究一探究二探究三解析:(1)设圆柱的底面半径为r,母线长为l, 变式训练2(1)若圆柱的轴截面是面积为9的正方形,则其底面圆的周长等于 ;?
(2)若一个圆锥的底面面积是9π,母线长为5,则其轴截面的面积等于 ;?
(3)用一个平面截半径为5 cm的球,球心到截面的距离为4 cm,求截面圆的面积.探究四探究一探究二探究三(2)设圆锥的底面半径为R,高为h,母线长为l(如图).
则πR2=9π,解得R=3.
因为l=5,答案:(1)3π (2)12 探究四探究一探究二探究三(3)解:如图所示,设AK为截面圆的半径,O为球心,则OK⊥AK.
在Rt△OAK中,OA=5 cm,OK=4 cm,故截面圆的面积S=π·AK2=9π cm2. 探究四探究一探究二探究三探究三棱柱、棱锥、棱台的结构特征
【例3】 (1)下列关于棱柱的性质正确的是( )
A.只有两个面相互平行
B.所有棱都相等
C.所有面都是四边形
D.各侧面都是平行四边形
(2)判断下列说法是否正确.
①棱锥的侧面不可能是正三角形;
②三棱锥中任何一个顶点都可作为棱锥的顶点,任何一个面都可作为棱锥的底面;
③棱锥被一个平面所截,一定得到一个棱锥和一个棱台;
④棱台的所有侧棱延长后可以不交于同一点.探究四探究一探究二探究三(1)解析:棱柱的两个底面一定是平行的,但在棱柱中并不一定只有两个面相互平行,故A错;棱柱所有的侧棱长都相等,但它们不一定等于底面多边形的边长,故B错;棱柱的侧面都是四边形,但底面可以不是四边形,故C错;棱柱的所有侧面都是平行四边形,故D正确,选D.
答案:D
(2)解:①错误.棱锥的侧面一定是三角形,可以是等腰三角形,也可以是正三角形,例如棱长均相等的正三棱锥的各个面都是正三角形.
②正确.在三棱锥中,共有4个面,每一个面均可作为底面,每一个顶点均可作为棱锥的顶点.
③错误.只有当棱锥被与其底面平行的平面所截时,才能截得一个棱锥和一个棱台.
④错误.任何一个棱台,将其所有侧棱延长后一定相交于同一点.探究四探究一探究二探究三反思感悟1.判断一个几何体是不是棱柱要紧扣棱柱的定义,同时要抓住以下三个关键点.
(1)底面:两个多边形全等,且所在平面互相平行.
(2)侧面:都是平行四边形.
(3)侧棱:互相平行,且相等.
以上三点缺一不可.
对于棱柱来说,其底面不一定是几何体的上、下两个面,也可以是左、右两个面或前、后两个面.探究四探究一探究二探究三2.判断一个几何体是棱锥、棱台的方法主要有以下两种.
(1)举反例法:
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法:探究四探究一探究二探究三变式训练3下列叙述正确的个数为 .?
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的几何体是棱台.
解析:①中的平面不一定平行于底面,故①错误.②③可用反例去检验,如图所示,故②③错误.
答案:0探究四探究一探究二探究三探究四探究四正棱锥、正棱台中的计算问题
【例4】若正四棱台两底面的面积分别为4和16,其高为 ,则正四棱台的侧棱长为 .?解析:作出正四棱台ABCD-A1B1C1D1,如图所示, 连接O1A1,OA,则四边形O1A1AO为直角梯形.
由正四棱台两底面的面积分别为4和16,
知A1B1=2,AB=4,探究一探究二探究三探究四反思感悟正棱锥、正棱台中的“直角图形”
1.正棱锥中的计算问题主要利用正棱锥中的3个直角三角形,即①侧棱、高和侧棱在底面上的射影组成的直角三角形;②斜高、高和斜高在底面上的射影组成的直角三角形;③侧棱、斜高和底面多边形边长的一半组成的直角三角形.
2.正棱台中的计算问题主要利用正棱台中的3个直角梯形,即①斜高、两底面的边心距以及两底面中心的连线组成的直角梯形;②侧棱、两底面中心的连线和两底面相应的外接圆半径组成的直角梯形;③斜高、侧棱和两底面边长的一半组成的直角梯形.另外,由于棱台是由棱锥所截得的,因此棱台问题可以转化为棱锥问题,即利用“还台为锥”的思想来解决.探究一探究二探究三探究四变式训练4在正三棱锥V-ABC中,若其底面边长为8,侧棱长为2 ,则它的高等于 .?解析:如图所示,设O是底面中心,则D为BC的中点,△VAO是直角三角形.123451.下列说法正确的是( )
A.圆锥的母线长等于底面圆的直径
B.圆柱的母线与轴垂直
C.圆台的母线与轴平行
D.球的直径必过球心
答案:D123452.如图所示的平面中的阴影部分绕虚线旋转一周,形成的几何体的形状为( )
A.一个球体
B.一个球体中间挖去一个圆柱
C.一个圆柱
D.一个球体中间挖去一个长方体
答案:B123453.一条直线被一个半径为13的球截得的线段长为24,则球心到直线的距离为( )
A.13 B.12 C.5 D.24答案:C 123454.如图所示,观察下面四个几何体,其中判断正确的是 ( )
A.①是棱台 B.②是圆台
C.③是棱锥 D.④不是棱柱
解析:图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图③是棱锥;图④前、后两个面平行,其他各面都是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱.故选C.
答案:C123455.以等腰梯形的对称轴为轴旋转一周而形成的旋转体是 .?
解析:等腰梯形的对称轴为两底中点的连线所在直线,此线把等腰梯形分成两个全等的直角梯形,旋转后形成圆台.
答案:圆台
(1)球面:以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面.
(2)球:球面所围成的几何体叫作球体,简称球.
(3)球的有关概念:
①球心:半圆的圆心.
②球的半径:连接球心和球面上任意一点的线段.
③球的直径:连接球面上两点并且过球心的线段.2.旋转体
(1)旋转面:一条平面曲线绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面.
(2)旋转体:封闭的旋转面围成的几何体叫作旋转体.(3)圆柱、圆锥、圆台
①定义:分别以矩形的一边、直角三角形的一条直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫作圆柱、圆锥、圆台.
②底面、侧面及侧面的母线:
底面:垂直于旋转轴的边旋转而成的圆面.
侧面:不垂直于旋转轴的边旋转而成的曲面.
侧面的母线:无论转到什么位置,不垂直于旋转轴的边.
③圆台也可以看作是用平行于圆锥底面的平面截这个圆锥而得到的.知识拓展四种常见简单旋转体的性质比较 3.多面体
我们把若干个平面多边形围成的几何体叫作多面体.其中棱柱、棱锥、棱台是简单多面体.
(1)棱柱
①定义:两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫作棱柱.
②有关概念③分类 正棱柱:底面是正多边形的直棱柱叫作正棱柱.
④表示:通常用底面各顶点的字母表示棱柱.如上图中的棱柱可记作:五棱柱ABCDE-A'B'C'D'E'.(2)棱锥
①定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.
②有关概念
③表示:用顶点和底面各顶点的字母表示棱锥.如上图中的棱锥可记作:四棱锥S-ABCD.④分类
按底面多边形的边数分为:三棱锥、四棱锥、五棱锥……,其中三棱锥也叫作四面体.(3)棱台
①定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.原棱锥的底面和截面叫作棱台的下底面和上底面,其他各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的侧棱.如图所示.②表示:用表示底面各顶点的字母表示棱台.如上图中的棱台可记作:四棱台ABCD-A'B'C'D'.
③分类:按底面多边形的边数分为三棱台、四棱台、五棱台……
④特殊的棱台:用正棱锥截得的棱台叫作正棱台.正棱台的侧面是全等的等腰梯形.归纳总结个棱柱、棱锥、棱台的性质比较 思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)过球面上的两点可作无数个大圆. ( )
(2)连接圆柱上、下底面圆周上两点的线段是圆柱的母线. ( )
(3)圆锥截去一个小圆锥后剩余部分是圆台. ( )
(4)每个面都是三角形的几何体就是棱锥. ( )
(5)有两个面互相平行,其余各面都是平行四边形的多面体就是棱柱. ( )× × √ × × 探究一探究二探究三分析:解答本题可先根据圆柱、圆锥、圆台、球的结构特征详细分析,再结合已知的各个命题的条件进行具体分析.探究一对旋转体有关概念及其结构特征的理解
【例1】 判断下列说法是否正确,并说明理由:
(1)圆柱的任意两条母线所在的直线是平行的;
(2)用一个平面截圆锥,得到一个圆锥和一个圆台;
(3)球是以半圆的直径所在的直线为旋转轴,半圆旋转一周形成的旋转体;
(4)圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线.探究四探究一探究二探究三解:(1)正确.由圆柱母线的定义知,圆柱的任意两条母线所在的直线是平行的.
(2)错误.用平行于圆锥底面的平面去截圆锥,才能得到一个圆锥和一个圆台,用不平行于圆锥底面的平面截圆锥,则不能得到一个圆锥和一个圆台.
(3)正确.由球的定义易知该说法正确.
(4)正确.由圆锥母线的定义知,圆锥顶点与底面圆周上任意一点的连线都是母线.反思感悟1.判断旋转体类型的关键是轴的确定,看旋转体是由平面图形绕哪条直线旋转所得,同一个平面图形绕不同的轴旋转,所得的旋转体一般是不同的.
2.球、圆柱、圆锥、圆台都是旋转体,但旋转体不仅仅是这几种几何体,也可以是这几种几何体的组合体.探究四探究一探究二探究三变式训练1如图(1)(2)所示的图形绕虚线旋转一周后形成的立体图形分别是由哪些简单几何体组成的?探究四探究一探究二探究三解:旋转后的图形如图所示.其中图①是由一个圆柱O1O2和两个圆台O2O3,O3O4组成的;图②是由一个圆锥O5O4,一个圆柱O3O4及一个圆台O1O3中挖去圆锥O2O1组成的.探究四探究一探究二探究三探究二简单旋转体中有关量的计算?
【例2】一个圆台的母线长为12 cm,两底面面积分别为4π cm2和25π cm2.求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.探究四探究一探究二探究三解:(1)设圆台的轴截面是等腰梯形ABCD,如图所示,由已知可得上底面的半径O1A=2 cm,下底面的半径OB=5 cm,腰长AB=12 cm,(2)设截得此圆台的圆锥的母线长为l cm,由△SAO1∽△SBO, 故截得此圆台的圆锥的母线长为20 cm.
反思感悟1.对于旋转体来说,轴截面既能揭示几何体各元素的数量关系,又能“化立体为平面”.
2.圆台一般都要先转化为圆锥,再进行计算或求值.探究四探究一探究二探究三解析:(1)设圆柱的底面半径为r,母线长为l, 变式训练2(1)若圆柱的轴截面是面积为9的正方形,则其底面圆的周长等于 ;?
(2)若一个圆锥的底面面积是9π,母线长为5,则其轴截面的面积等于 ;?
(3)用一个平面截半径为5 cm的球,球心到截面的距离为4 cm,求截面圆的面积.探究四探究一探究二探究三(2)设圆锥的底面半径为R,高为h,母线长为l(如图).
则πR2=9π,解得R=3.
因为l=5,答案:(1)3π (2)12 探究四探究一探究二探究三(3)解:如图所示,设AK为截面圆的半径,O为球心,则OK⊥AK.
在Rt△OAK中,OA=5 cm,OK=4 cm,故截面圆的面积S=π·AK2=9π cm2. 探究四探究一探究二探究三探究三棱柱、棱锥、棱台的结构特征
【例3】 (1)下列关于棱柱的性质正确的是( )
A.只有两个面相互平行
B.所有棱都相等
C.所有面都是四边形
D.各侧面都是平行四边形
(2)判断下列说法是否正确.
①棱锥的侧面不可能是正三角形;
②三棱锥中任何一个顶点都可作为棱锥的顶点,任何一个面都可作为棱锥的底面;
③棱锥被一个平面所截,一定得到一个棱锥和一个棱台;
④棱台的所有侧棱延长后可以不交于同一点.探究四探究一探究二探究三(1)解析:棱柱的两个底面一定是平行的,但在棱柱中并不一定只有两个面相互平行,故A错;棱柱所有的侧棱长都相等,但它们不一定等于底面多边形的边长,故B错;棱柱的侧面都是四边形,但底面可以不是四边形,故C错;棱柱的所有侧面都是平行四边形,故D正确,选D.
答案:D
(2)解:①错误.棱锥的侧面一定是三角形,可以是等腰三角形,也可以是正三角形,例如棱长均相等的正三棱锥的各个面都是正三角形.
②正确.在三棱锥中,共有4个面,每一个面均可作为底面,每一个顶点均可作为棱锥的顶点.
③错误.只有当棱锥被与其底面平行的平面所截时,才能截得一个棱锥和一个棱台.
④错误.任何一个棱台,将其所有侧棱延长后一定相交于同一点.探究四探究一探究二探究三反思感悟1.判断一个几何体是不是棱柱要紧扣棱柱的定义,同时要抓住以下三个关键点.
(1)底面:两个多边形全等,且所在平面互相平行.
(2)侧面:都是平行四边形.
(3)侧棱:互相平行,且相等.
以上三点缺一不可.
对于棱柱来说,其底面不一定是几何体的上、下两个面,也可以是左、右两个面或前、后两个面.探究四探究一探究二探究三2.判断一个几何体是棱锥、棱台的方法主要有以下两种.
(1)举反例法:
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法:探究四探究一探究二探究三变式训练3下列叙述正确的个数为 .?
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余四个面都是等腰梯形的几何体是棱台.
解析:①中的平面不一定平行于底面,故①错误.②③可用反例去检验,如图所示,故②③错误.
答案:0探究四探究一探究二探究三探究四探究四正棱锥、正棱台中的计算问题
【例4】若正四棱台两底面的面积分别为4和16,其高为 ,则正四棱台的侧棱长为 .?解析:作出正四棱台ABCD-A1B1C1D1,如图所示, 连接O1A1,OA,则四边形O1A1AO为直角梯形.
由正四棱台两底面的面积分别为4和16,
知A1B1=2,AB=4,探究一探究二探究三探究四反思感悟正棱锥、正棱台中的“直角图形”
1.正棱锥中的计算问题主要利用正棱锥中的3个直角三角形,即①侧棱、高和侧棱在底面上的射影组成的直角三角形;②斜高、高和斜高在底面上的射影组成的直角三角形;③侧棱、斜高和底面多边形边长的一半组成的直角三角形.
2.正棱台中的计算问题主要利用正棱台中的3个直角梯形,即①斜高、两底面的边心距以及两底面中心的连线组成的直角梯形;②侧棱、两底面中心的连线和两底面相应的外接圆半径组成的直角梯形;③斜高、侧棱和两底面边长的一半组成的直角梯形.另外,由于棱台是由棱锥所截得的,因此棱台问题可以转化为棱锥问题,即利用“还台为锥”的思想来解决.探究一探究二探究三探究四变式训练4在正三棱锥V-ABC中,若其底面边长为8,侧棱长为2 ,则它的高等于 .?解析:如图所示,设O是底面中心,则D为BC的中点,△VAO是直角三角形.123451.下列说法正确的是( )
A.圆锥的母线长等于底面圆的直径
B.圆柱的母线与轴垂直
C.圆台的母线与轴平行
D.球的直径必过球心
答案:D123452.如图所示的平面中的阴影部分绕虚线旋转一周,形成的几何体的形状为( )
A.一个球体
B.一个球体中间挖去一个圆柱
C.一个圆柱
D.一个球体中间挖去一个长方体
答案:B123453.一条直线被一个半径为13的球截得的线段长为24,则球心到直线的距离为( )
A.13 B.12 C.5 D.24答案:C 123454.如图所示,观察下面四个几何体,其中判断正确的是 ( )
A.①是棱台 B.②是圆台
C.③是棱锥 D.④不是棱柱
解析:图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图③是棱锥;图④前、后两个面平行,其他各面都是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱.故选C.
答案:C123455.以等腰梯形的对称轴为轴旋转一周而形成的旋转体是 .?
解析:等腰梯形的对称轴为两底中点的连线所在直线,此线把等腰梯形分成两个全等的直角梯形,旋转后形成圆台.
答案:圆台
