2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.4.1空间图形的基本关系与公理(44张))
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.4.1空间图形的基本关系与公理(44张)) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览




文档简介
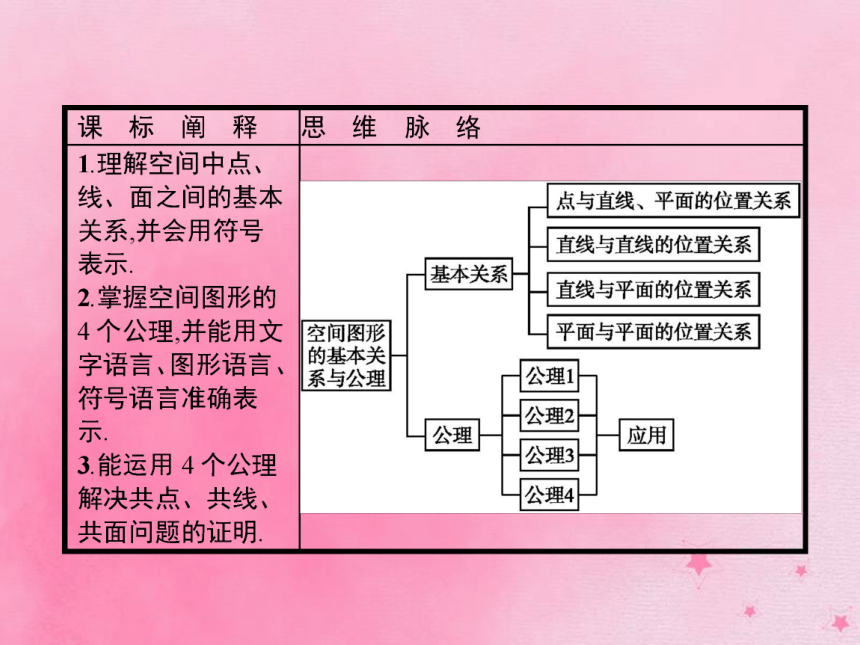
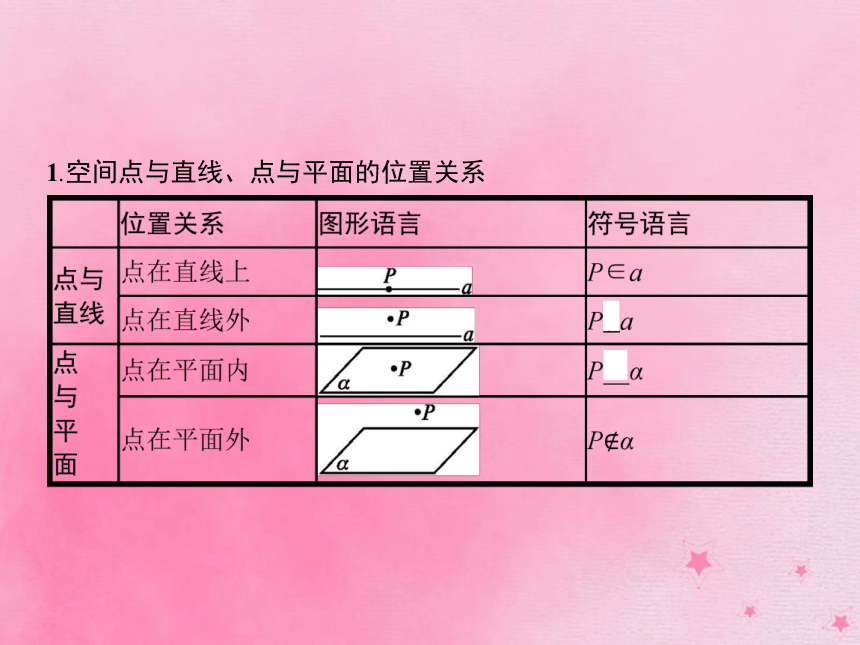
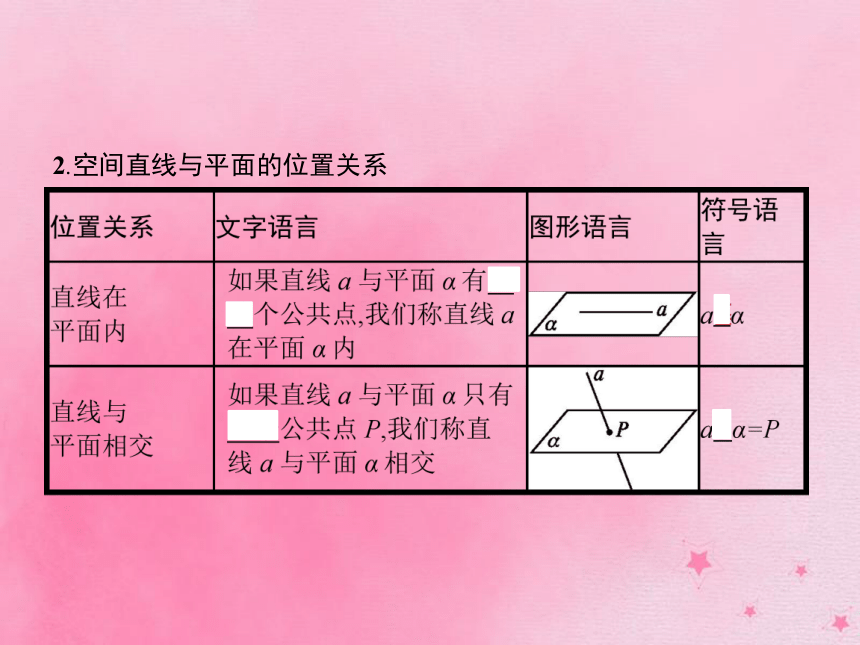
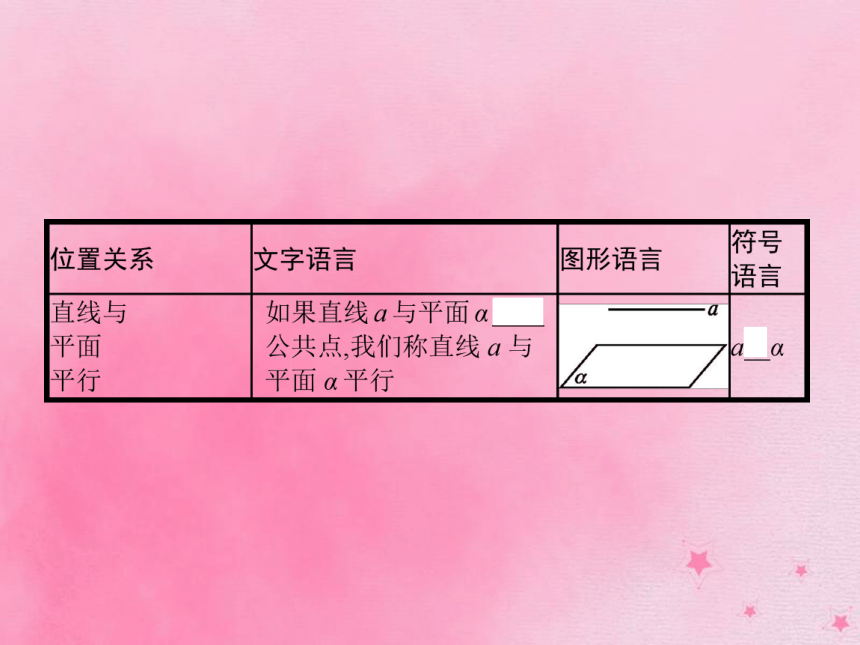
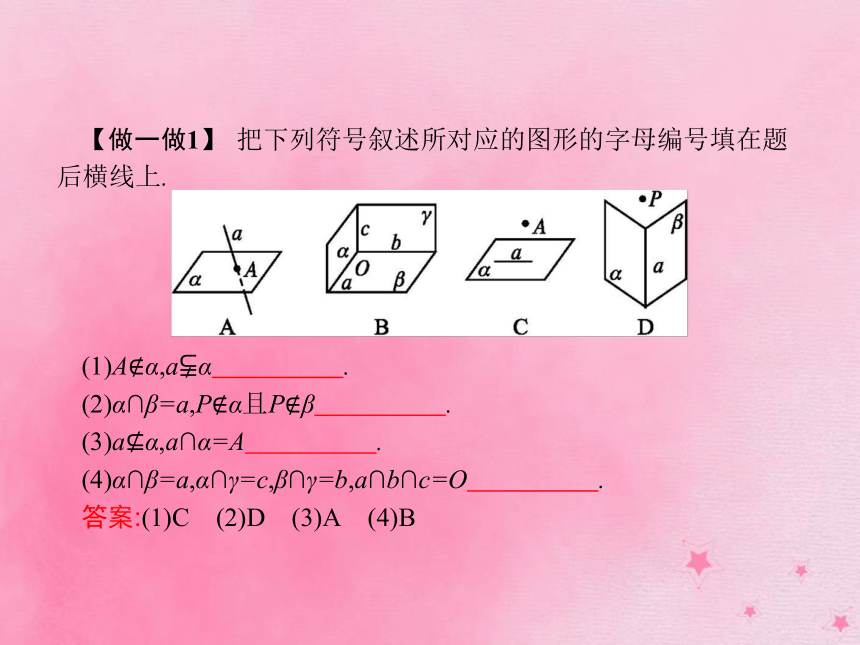
课件44张PPT。§4 空间图形的基本关系与公理第1课时 空间图形的基本关系与公理1.空间点与直线、点与平面的位置关系 2.空间直线与平面的位置关系 【做一做1】 把下列符号叙述所对应的图形的字母编号填在题后横线上.
(1)A?α,a?α .?
(2)α∩β=a,P?α且P?β .?
(3)a?α,a∩α=A .?
(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O .?
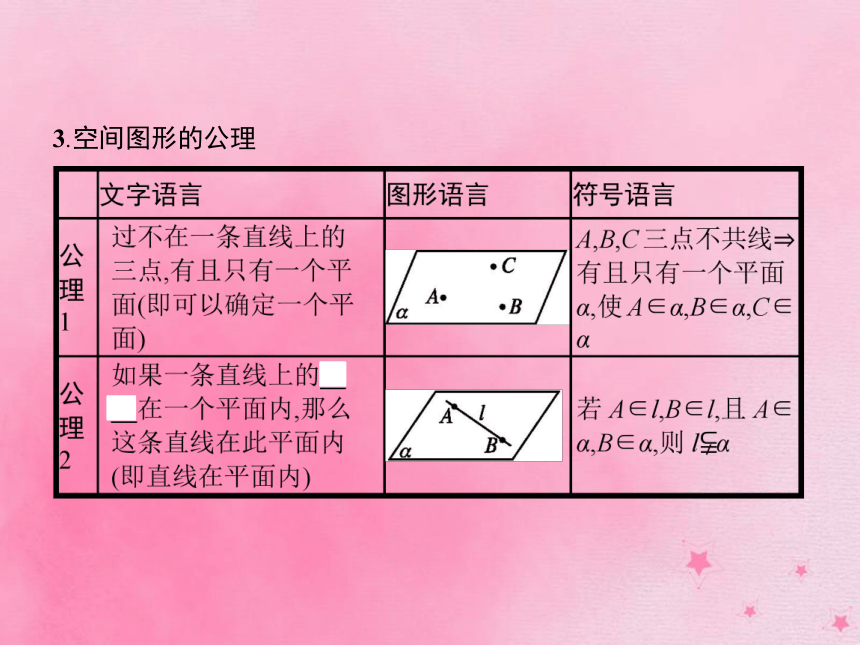
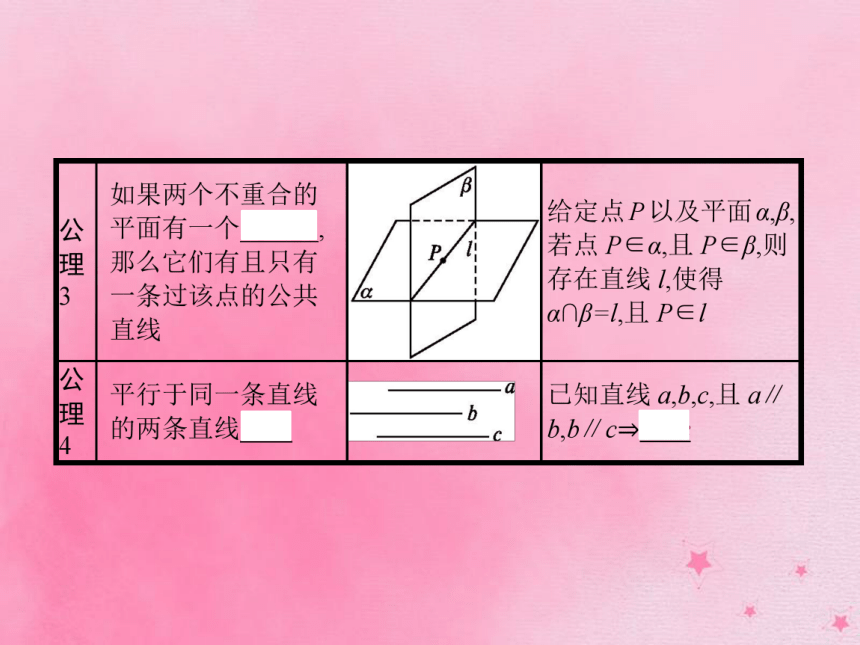
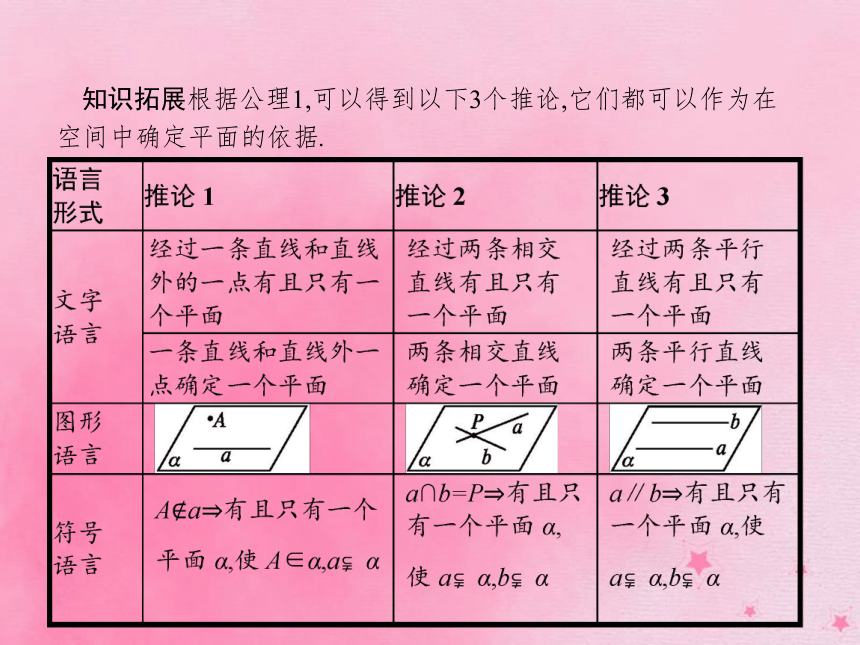
答案:(1)C (2)D (3)A (4)B名师点拨直线与平面平行和直线与平面相交统称为直线在平面外,即3.空间图形的公理 知识拓展根据公理1,可以得到以下3个推论,它们都可以作为在空间中确定平面的依据.【做一做2】 下列说法正确的是( )
A.三点确定一个平面
B.四边形一定是平面图形
C.三角形一定是平面图形
D.平面α和平面β有不同在一条直线上的三个交点
解析:本题考查平面的基本知识.A选项,当三点共线时有无数多个平面;B选项,四边形有空间四边形与平面四边形之分;C选项,三角形的三个顶点不共线,根据公理1可知三角形的三个顶点确定一个平面;D选项,若具有D选项中的条件,则α与β重合.故选C.
答案:C【做一做3】 如图所示,点A在平面α内,点B也在平面α内,点C在直线AB上.
(1)用符号语言表示上述位置关系;
(2)判断点C与平面α的关系.
分析:由公理2可知AB在平面α内,而点C在直线AB上,所以点C在平面α内.
解:(1)A∈α,B∈α,C∈AB.
(2)因为A∈α,B∈α,所以AB?α.
又因为C∈AB,所以C∈α.4.空间平面与平面的位置关系(除重合外) 5.空间两条直线的位置关系 【做一做4】 已知a,b是异面直线,直线c∥a,则c与b ( )
A.一定是异面直线 B.一定是相交直线
C.不可能是平行直线 D.不可能是相交直线
解析:若a,b异面,c∥a,则c与b相交或异面,故C正确.
答案:C思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)如果直线a与直线b是异面直线,直线b与直线c也是异面直线,那么直线a与直线c也一定是异面直线. ( )
(2)如果两个平面有三个公共点,那么这两个平面必重合. ( )
(3)平面α与平面β会只有一个公共点. ( )
(4)不共线的四点最多可确定4个平面. ( )
(5)两两相交的三条直线必共面. ( )× × × √ × 探究一探究二探究三探究四易错辨析证明:如图所示,已知l1∩l2=A,l2∩l3=B,l1∩l3=C.
方法一(同一法)
∵l1∩l2=A,∴l1和l2确定一个平面α.
∵l2∩l3=B,∴B∈l2.又l2?α,∴B∈α.
同理可证C∈α.又B∈l3,C∈l3,∴l3?α.
∴直线l1,l2,l3在同一平面内.探究一公理1的应用
【例1】 证明:两两相交,且不共点的三条直线在同一平面内.探究一探究二探究三探究四易错辨析方法二(重合法)
∵l1∩l2=A,∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2?α,∴A∈α.
∵A∈l2,l2?β,∴A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
∴不共线的三个点A,B,C既在平面α内,又在平面β内.∴平面α和β重合,即直线l1,l2,l3在同一平面内.探究一探究二探究三探究四易错辨析反思感悟1.公理1的主要作用有两个:一是作为确定平面的依据,判断若干个点或线能否确定平面,确定几个平面等;二是证明点线共面.
2.证明点线共面问题的基本方法主要有以下两种:探究一探究二探究三探究四易错辨析延伸探究(1)把【例1】中的“不共点”删掉呢?这三条直线是否共面?
(2)把【例1】中“三条直线”改为“四条直线”呢?这四条直线是否共面?试证明你的结论.
解:(1)不一定共面.
①若三条直线两两相交,且过同一个点.
这三条直线在同一个平面内相交,如图.
这三条直线不共面.如图.探究一探究二探究三探究四易错辨析②若三条直线两两相交,且不共点,由【例1】可知,这三条直线共面.
(2)共面.
已知:a,b,c,d四条直线两两相交,且不共点.
求证:a,b,c,d四线共面.
证明:①无三线共点情况,如图.
设a∩d=M,b∩d=N,c∩d=P,a∩b=Q,a∩c=R,b∩c=S.
因为a∩d=M,所以a,d可确定一个平面α.
因为N∈d,Q∈a,所以N∈α,Q∈α,
所以NQ?α,即b?α.
同理,c?α,所以a,b,c,d共面.探究一探究二探究三探究四易错辨析②有三线共点的情况,如图.
设b,c,d三线相交于点K,与a分别交于N,P,M且K?a,
因为K?a,所以K和a确定一个平面,设为β.
因为N∈a,a?β,所以N∈β.所以NK?β,即b?β.
同理,c?β,d?β.
所以a,b,c,d共面.
由①②知,a,b,c,d共面.探究一探究二探究三探究四易错辨析【例2】 如图所示,在正方体ABCD-A'B'C'D'中,M,N分别是所在棱的中点,连接D'M,并延长交C'B'的延长线于点E,连接C'N并延长,交CB的延长线于点F.
求证:直线EF?平面BCC'B'.分析:要证明直线在平面内,需说明直线上有两个点在这个平面内.
证明:∵B∈平面BCC'B',C∈平面BCC'B',
∴直线BC?平面BCC'B'.
又C'N∩CB=F,∴F∈CB,∴F∈平面BCC'B'.
同理可得E∈平面BCC'B'.
∴直线EF?平面BCC'B'.探究二公理2的应用 探究一探究二探究三探究四易错辨析反思感悟公理2的作用有两个:(1)用直线检验平面;(2)判断直线是否在平面内.要证明直线在平面内,只需要在直线上找到两个点,证明这两个点都在这个平面内,直线就在这个平面内,解决问题的关键就在于寻找这样的点.探究一探究二探究三探究四易错辨析变式训练1若l1∥l2,l3与l1,l2分别相交于点C,B.求证:l1,l2,l3在同一平面内.
证明:∵l1∥l2,∴l1,l2确定一个平面记为α.
∵l1∩l3=C,∴C∈l1.
∵l1?α,∴C∈α.
∵l2∩l3=B,∴B∈l2.∵l2?α,∴B∈α.
∵B∈l3,C∈l3,∴l3?α,即l1,l2,l3在同一平面内.探究一探究二探究三探究四易错辨析【例3】 如图所示,在棱长均相等的正三棱锥A-BCD中,E,G分别为BC,AB的中点,点F在CD上,点H在AD上,且有DF∶FC=DH∶HA=2∶3,求证:EF,GH,BD交于一点.
分析:先证明GH和EF共面且交于一点O,再说明O是平面ABD和平面BCD的公共点,而平面ABD和平面BCD相交于直线BD,根据公理3,两个平面相交,有且只有一条交线.因此点O在交线上,即点O在直线BD上.从而证明了直线EF,GH,BD都过点O.探究三公理3的应用 探究一探究二探究三探究四易错辨析证明:因为E,G分别为BC,AB的中点, 所以FH∥GE,FH≠GE.
所以四边形EFHG是一个梯形.
设GH与EF相交于点O,则O在平面ABD内,又在平面BCD内,所以O在平面ABD与平面BCD的交线上,而这两个平面的交线是BD,且交线只有一条,
所以点O在直线BD上.所以EF,GH,BD交于一点.探究一探究二探究三探究四易错辨析反思感悟1.公理3的主要作用:(1)判断两个平面是否相交;(2)证明点在直线上;(3)证明共线问题;(4)证明共点问题.
2.证明多点共线通常利用公理3,即两个相交平面的交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,证明其他点也在这条直线上.
3.证明三线共点问题可先把其中一条作为分别过其余两条直线的两个平面的交线,再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.探究一探究二探究三探究四易错辨析变式训练2如图所示,在正方体ABCD-A1B1C1D1中,A1C与平面BDC1交于点M,BD与AC交于点O,则( )
A.M∈BC1
B.M∈DC1
C.M∈C1O
D.M∈B1B
解析:因为M∈A1C,A1C?平面A1ACC1,
所以M∈平面A1ACC1.
因为M∈平面BDC1,且平面A1ACC1∩平面BDC1=C1O,所以M∈C1O.故选C.
答案:C探究一探究二探究三探究四易错辨析【例4】 如图所示,点P是△ABC所在平面外一点,点D,E分别是△PAB和△PBC的重心.求证:DE∥AC,DE= AC.探究四公理4的应用 探究一探究二探究三探究四易错辨析证明:如图所示,连接PD,PE,并延长分别交AB,BC于点M,N.
因为点D,E分别是△PAB,△PBC的重心,所以M,N分别是AB,BC的中点.探究一探究二探究三探究四易错辨析反思感悟空间中证明两条直线平行的方法:
(1)借助平面几何知识,如三角形的中位线性质、平行四边形的性质、成比例的线段平行.
(2)利用公理4,即证明两条直线都与第三条直线平行.探究一探究二探究三探究四易错辨析变式训练3如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱A1A,C1C的中点,求证:四边形MBND1为平行四边形.证明:取B1B的中点P,连接C1P,MP.
因为N为C1C的中点,
由正方体的性质知C1N??PB,
所以四边形C1PBN为平行四边形,
所以C1P??BN.
又M,P分别为A1A,B1B的中点,
所以MP??A1B1.
又由正方体的性质知A1B1??C1D1,所以MP??C1D1,
所以四边形D1MPC1为平行四边形,
所以C1P??MD1.所以MD1??BN,
所以四边形MBND1为平行四边形.探究一探究二探究三探究四易错辨析对点、线、面的位置关系考虑不全而致误
【典例】 已知空间四点,如果任意三点都不共线,那么由这四点可以确定多少个平面?说明理由.
错解因为不共线的三点确定一个平面,所以由题设条件中的四点可确定四个平面.
正解空间任意三点都不共线的四个点有两种位置关系:
第一种,当由其中任意不共线的三点所确定的平面都过第四个点时,由这四个点只能确定一个平面;
第二种,当由其中任意不共线的三点所确定的平面都不过第四个点时,由这四个点可确定四个平面.
综上所述,由题设条件中的四点可确定一个或四个平面.探究一探究二探究三探究四易错辨析纠错心得1.对于确定平面个数问题,在讨论中要全面考虑,尤其要先分清给出几个点的可能的位置关系,再进行分类讨论.
2.可借助正方体、三棱锥等特殊几何体进行直观观察.探究一探究二探究三探究四易错辨析变式训练已知空间不同的五个点.
(1)若有某四点共面,则这五点最多可确定多少个平面?
(2)若任意四点都在同一平面内,则这五点共能确定多少个平面?并证明你的结论.探究一探究二探究三探究四易错辨析解:(1)当共面的四点任意三点不共线,另一点不在该平面内时,这五点确定的平面最多,如图所示,最多可确定7个平面.
(2)若任意四点都在同一平面内,这五点必共面.
证明如下:若A,B,C,D四点在平面α内,又A,B,C,P在同一平面内,可分如下情况证明:
①若A,B,C三点不共线,则平面α为A,B,C确定的平面,所以点P在平面内,故五点共面.
②若A,B,C三点在直线l上,则当点D或P也在l上时,五点共面;若点D,P都不在l上,则直线DP与直线AB必在A,B,D,P所在的平面内,故点C也在这一平面内,从而五点也共面.123451.如图所示,该图形用符号语言可表示为( )
A.α∩β=m,n?α,m∩n=A
B.α∩β=m,n∈α,m∩n=A
C.α∩β=m,n?α,A?m,A?n
D.α∩β=m,n∈α,A∈m,A∈n
答案:A123452.有下列四种说法:
①过三个点确定一个平面;
②矩形是平面图形;
③三条直线两两相交,则它们确定一个平面;
④两个相交平面把空间分成四个区域.
其中错误的序号是( )
A.①和② B.①和③
C.②和④ D.②和③
解析:只有不共线的三点才能确定一个平面,故①错;三条直线两两相交,交于三点时,确定一个平面;交于一点时,可确定一个或三个平面,故③错.故选B.
答案:B123453.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,H,G分别为BC,CD的中点,则( )
A.BD∥平面EFGH,且四边形EFGH是矩形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是菱形
D.EH∥平面ADC,且四边形EFGH是平行四边形12345解析:如图所示,连接BD.
∵AE∶EB=AF∶FD=1∶4,
∴EF?? BD.
∵EF?平面BCD,BD?平面BCD,
∴EF∥平面BCD.
又H,G分别为BC,CD的中点,
∴HG?? BD,∴EF∥HG,且EF≠HG,
故四边形EFGH为梯形.
答案:B123454.设平面α与平面β相交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β= .?
答案:C123455.如图所示,在空间四边形各边AD,AB,BC,CD上分别取E,F,G,H四点,如果EF,GH交于一点P,求证:点P在直线BD上.
证明:∵EF∩GH=P,
∴P∈EF且P∈GH.
∵EF?平面ABD,GH?平面CBD,
∴P∈平面ABD,且P∈平面CBD,
∴P∈平面ABD∩平面CBD.
∵平面ABD∩平面CBD=BD,∴P∈BD,
∴点P在直线BD上.
(1)A?α,a?α .?
(2)α∩β=a,P?α且P?β .?
(3)a?α,a∩α=A .?
(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O .?
答案:(1)C (2)D (3)A (4)B名师点拨直线与平面平行和直线与平面相交统称为直线在平面外,即3.空间图形的公理 知识拓展根据公理1,可以得到以下3个推论,它们都可以作为在空间中确定平面的依据.【做一做2】 下列说法正确的是( )
A.三点确定一个平面
B.四边形一定是平面图形
C.三角形一定是平面图形
D.平面α和平面β有不同在一条直线上的三个交点
解析:本题考查平面的基本知识.A选项,当三点共线时有无数多个平面;B选项,四边形有空间四边形与平面四边形之分;C选项,三角形的三个顶点不共线,根据公理1可知三角形的三个顶点确定一个平面;D选项,若具有D选项中的条件,则α与β重合.故选C.
答案:C【做一做3】 如图所示,点A在平面α内,点B也在平面α内,点C在直线AB上.
(1)用符号语言表示上述位置关系;
(2)判断点C与平面α的关系.
分析:由公理2可知AB在平面α内,而点C在直线AB上,所以点C在平面α内.
解:(1)A∈α,B∈α,C∈AB.
(2)因为A∈α,B∈α,所以AB?α.
又因为C∈AB,所以C∈α.4.空间平面与平面的位置关系(除重合外) 5.空间两条直线的位置关系 【做一做4】 已知a,b是异面直线,直线c∥a,则c与b ( )
A.一定是异面直线 B.一定是相交直线
C.不可能是平行直线 D.不可能是相交直线
解析:若a,b异面,c∥a,则c与b相交或异面,故C正确.
答案:C思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)如果直线a与直线b是异面直线,直线b与直线c也是异面直线,那么直线a与直线c也一定是异面直线. ( )
(2)如果两个平面有三个公共点,那么这两个平面必重合. ( )
(3)平面α与平面β会只有一个公共点. ( )
(4)不共线的四点最多可确定4个平面. ( )
(5)两两相交的三条直线必共面. ( )× × × √ × 探究一探究二探究三探究四易错辨析证明:如图所示,已知l1∩l2=A,l2∩l3=B,l1∩l3=C.
方法一(同一法)
∵l1∩l2=A,∴l1和l2确定一个平面α.
∵l2∩l3=B,∴B∈l2.又l2?α,∴B∈α.
同理可证C∈α.又B∈l3,C∈l3,∴l3?α.
∴直线l1,l2,l3在同一平面内.探究一公理1的应用
【例1】 证明:两两相交,且不共点的三条直线在同一平面内.探究一探究二探究三探究四易错辨析方法二(重合法)
∵l1∩l2=A,∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2?α,∴A∈α.
∵A∈l2,l2?β,∴A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
∴不共线的三个点A,B,C既在平面α内,又在平面β内.∴平面α和β重合,即直线l1,l2,l3在同一平面内.探究一探究二探究三探究四易错辨析反思感悟1.公理1的主要作用有两个:一是作为确定平面的依据,判断若干个点或线能否确定平面,确定几个平面等;二是证明点线共面.
2.证明点线共面问题的基本方法主要有以下两种:探究一探究二探究三探究四易错辨析延伸探究(1)把【例1】中的“不共点”删掉呢?这三条直线是否共面?
(2)把【例1】中“三条直线”改为“四条直线”呢?这四条直线是否共面?试证明你的结论.
解:(1)不一定共面.
①若三条直线两两相交,且过同一个点.
这三条直线在同一个平面内相交,如图.
这三条直线不共面.如图.探究一探究二探究三探究四易错辨析②若三条直线两两相交,且不共点,由【例1】可知,这三条直线共面.
(2)共面.
已知:a,b,c,d四条直线两两相交,且不共点.
求证:a,b,c,d四线共面.
证明:①无三线共点情况,如图.
设a∩d=M,b∩d=N,c∩d=P,a∩b=Q,a∩c=R,b∩c=S.
因为a∩d=M,所以a,d可确定一个平面α.
因为N∈d,Q∈a,所以N∈α,Q∈α,
所以NQ?α,即b?α.
同理,c?α,所以a,b,c,d共面.探究一探究二探究三探究四易错辨析②有三线共点的情况,如图.
设b,c,d三线相交于点K,与a分别交于N,P,M且K?a,
因为K?a,所以K和a确定一个平面,设为β.
因为N∈a,a?β,所以N∈β.所以NK?β,即b?β.
同理,c?β,d?β.
所以a,b,c,d共面.
由①②知,a,b,c,d共面.探究一探究二探究三探究四易错辨析【例2】 如图所示,在正方体ABCD-A'B'C'D'中,M,N分别是所在棱的中点,连接D'M,并延长交C'B'的延长线于点E,连接C'N并延长,交CB的延长线于点F.
求证:直线EF?平面BCC'B'.分析:要证明直线在平面内,需说明直线上有两个点在这个平面内.
证明:∵B∈平面BCC'B',C∈平面BCC'B',
∴直线BC?平面BCC'B'.
又C'N∩CB=F,∴F∈CB,∴F∈平面BCC'B'.
同理可得E∈平面BCC'B'.
∴直线EF?平面BCC'B'.探究二公理2的应用 探究一探究二探究三探究四易错辨析反思感悟公理2的作用有两个:(1)用直线检验平面;(2)判断直线是否在平面内.要证明直线在平面内,只需要在直线上找到两个点,证明这两个点都在这个平面内,直线就在这个平面内,解决问题的关键就在于寻找这样的点.探究一探究二探究三探究四易错辨析变式训练1若l1∥l2,l3与l1,l2分别相交于点C,B.求证:l1,l2,l3在同一平面内.
证明:∵l1∥l2,∴l1,l2确定一个平面记为α.
∵l1∩l3=C,∴C∈l1.
∵l1?α,∴C∈α.
∵l2∩l3=B,∴B∈l2.∵l2?α,∴B∈α.
∵B∈l3,C∈l3,∴l3?α,即l1,l2,l3在同一平面内.探究一探究二探究三探究四易错辨析【例3】 如图所示,在棱长均相等的正三棱锥A-BCD中,E,G分别为BC,AB的中点,点F在CD上,点H在AD上,且有DF∶FC=DH∶HA=2∶3,求证:EF,GH,BD交于一点.
分析:先证明GH和EF共面且交于一点O,再说明O是平面ABD和平面BCD的公共点,而平面ABD和平面BCD相交于直线BD,根据公理3,两个平面相交,有且只有一条交线.因此点O在交线上,即点O在直线BD上.从而证明了直线EF,GH,BD都过点O.探究三公理3的应用 探究一探究二探究三探究四易错辨析证明:因为E,G分别为BC,AB的中点, 所以FH∥GE,FH≠GE.
所以四边形EFHG是一个梯形.
设GH与EF相交于点O,则O在平面ABD内,又在平面BCD内,所以O在平面ABD与平面BCD的交线上,而这两个平面的交线是BD,且交线只有一条,
所以点O在直线BD上.所以EF,GH,BD交于一点.探究一探究二探究三探究四易错辨析反思感悟1.公理3的主要作用:(1)判断两个平面是否相交;(2)证明点在直线上;(3)证明共线问题;(4)证明共点问题.
2.证明多点共线通常利用公理3,即两个相交平面的交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,证明其他点也在这条直线上.
3.证明三线共点问题可先把其中一条作为分别过其余两条直线的两个平面的交线,再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.探究一探究二探究三探究四易错辨析变式训练2如图所示,在正方体ABCD-A1B1C1D1中,A1C与平面BDC1交于点M,BD与AC交于点O,则( )
A.M∈BC1
B.M∈DC1
C.M∈C1O
D.M∈B1B
解析:因为M∈A1C,A1C?平面A1ACC1,
所以M∈平面A1ACC1.
因为M∈平面BDC1,且平面A1ACC1∩平面BDC1=C1O,所以M∈C1O.故选C.
答案:C探究一探究二探究三探究四易错辨析【例4】 如图所示,点P是△ABC所在平面外一点,点D,E分别是△PAB和△PBC的重心.求证:DE∥AC,DE= AC.探究四公理4的应用 探究一探究二探究三探究四易错辨析证明:如图所示,连接PD,PE,并延长分别交AB,BC于点M,N.
因为点D,E分别是△PAB,△PBC的重心,所以M,N分别是AB,BC的中点.探究一探究二探究三探究四易错辨析反思感悟空间中证明两条直线平行的方法:
(1)借助平面几何知识,如三角形的中位线性质、平行四边形的性质、成比例的线段平行.
(2)利用公理4,即证明两条直线都与第三条直线平行.探究一探究二探究三探究四易错辨析变式训练3如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱A1A,C1C的中点,求证:四边形MBND1为平行四边形.证明:取B1B的中点P,连接C1P,MP.
因为N为C1C的中点,
由正方体的性质知C1N??PB,
所以四边形C1PBN为平行四边形,
所以C1P??BN.
又M,P分别为A1A,B1B的中点,
所以MP??A1B1.
又由正方体的性质知A1B1??C1D1,所以MP??C1D1,
所以四边形D1MPC1为平行四边形,
所以C1P??MD1.所以MD1??BN,
所以四边形MBND1为平行四边形.探究一探究二探究三探究四易错辨析对点、线、面的位置关系考虑不全而致误
【典例】 已知空间四点,如果任意三点都不共线,那么由这四点可以确定多少个平面?说明理由.
错解因为不共线的三点确定一个平面,所以由题设条件中的四点可确定四个平面.
正解空间任意三点都不共线的四个点有两种位置关系:
第一种,当由其中任意不共线的三点所确定的平面都过第四个点时,由这四个点只能确定一个平面;
第二种,当由其中任意不共线的三点所确定的平面都不过第四个点时,由这四个点可确定四个平面.
综上所述,由题设条件中的四点可确定一个或四个平面.探究一探究二探究三探究四易错辨析纠错心得1.对于确定平面个数问题,在讨论中要全面考虑,尤其要先分清给出几个点的可能的位置关系,再进行分类讨论.
2.可借助正方体、三棱锥等特殊几何体进行直观观察.探究一探究二探究三探究四易错辨析变式训练已知空间不同的五个点.
(1)若有某四点共面,则这五点最多可确定多少个平面?
(2)若任意四点都在同一平面内,则这五点共能确定多少个平面?并证明你的结论.探究一探究二探究三探究四易错辨析解:(1)当共面的四点任意三点不共线,另一点不在该平面内时,这五点确定的平面最多,如图所示,最多可确定7个平面.
(2)若任意四点都在同一平面内,这五点必共面.
证明如下:若A,B,C,D四点在平面α内,又A,B,C,P在同一平面内,可分如下情况证明:
①若A,B,C三点不共线,则平面α为A,B,C确定的平面,所以点P在平面内,故五点共面.
②若A,B,C三点在直线l上,则当点D或P也在l上时,五点共面;若点D,P都不在l上,则直线DP与直线AB必在A,B,D,P所在的平面内,故点C也在这一平面内,从而五点也共面.123451.如图所示,该图形用符号语言可表示为( )
A.α∩β=m,n?α,m∩n=A
B.α∩β=m,n∈α,m∩n=A
C.α∩β=m,n?α,A?m,A?n
D.α∩β=m,n∈α,A∈m,A∈n
答案:A123452.有下列四种说法:
①过三个点确定一个平面;
②矩形是平面图形;
③三条直线两两相交,则它们确定一个平面;
④两个相交平面把空间分成四个区域.
其中错误的序号是( )
A.①和② B.①和③
C.②和④ D.②和③
解析:只有不共线的三点才能确定一个平面,故①错;三条直线两两相交,交于三点时,确定一个平面;交于一点时,可确定一个或三个平面,故③错.故选B.
答案:B123453.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,H,G分别为BC,CD的中点,则( )
A.BD∥平面EFGH,且四边形EFGH是矩形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是菱形
D.EH∥平面ADC,且四边形EFGH是平行四边形12345解析:如图所示,连接BD.
∵AE∶EB=AF∶FD=1∶4,
∴EF?? BD.
∵EF?平面BCD,BD?平面BCD,
∴EF∥平面BCD.
又H,G分别为BC,CD的中点,
∴HG?? BD,∴EF∥HG,且EF≠HG,
故四边形EFGH为梯形.
答案:B123454.设平面α与平面β相交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β= .?
答案:C123455.如图所示,在空间四边形各边AD,AB,BC,CD上分别取E,F,G,H四点,如果EF,GH交于一点P,求证:点P在直线BD上.
证明:∵EF∩GH=P,
∴P∈EF且P∈GH.
∵EF?平面ABD,GH?平面CBD,
∴P∈平面ABD,且P∈平面CBD,
∴P∈平面ABD∩平面CBD.
∵平面ABD∩平面CBD=BD,∴P∈BD,
∴点P在直线BD上.
