2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.4.2等角定理与异面直线所成的角(28张))
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.4.2等角定理与异面直线所成的角(28张)) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览





文档简介
课件28张PPT。第2课时 等角定理与异面直线所成的角1.等角定理
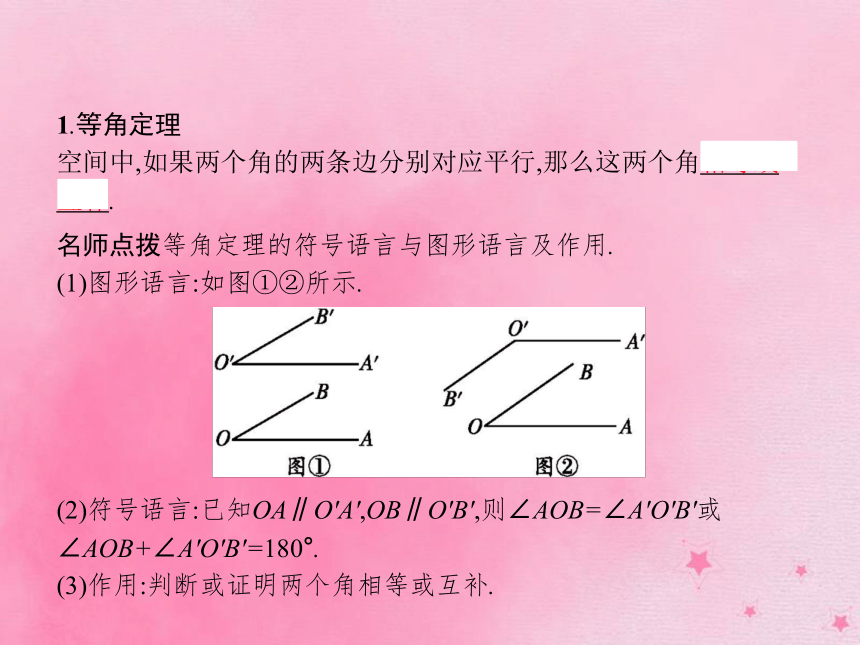
空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补.名师点拨等角定理的符号语言与图形语言及作用.
(1)图形语言:如图①②所示.
(2)符号语言:已知OA∥O'A',OB∥O'B',则∠AOB=∠A'O'B'或∠AOB+∠A'O'B'=180°.
(3)作用:判断或证明两个角相等或互补.【做一做1】 空间两个角α,β的两边分别对应平行,且方向相同,若α=50°,则β等于( )
A.50° B.130°
C.40° D.50°或130°
解析:由等角定理知β与α相等.
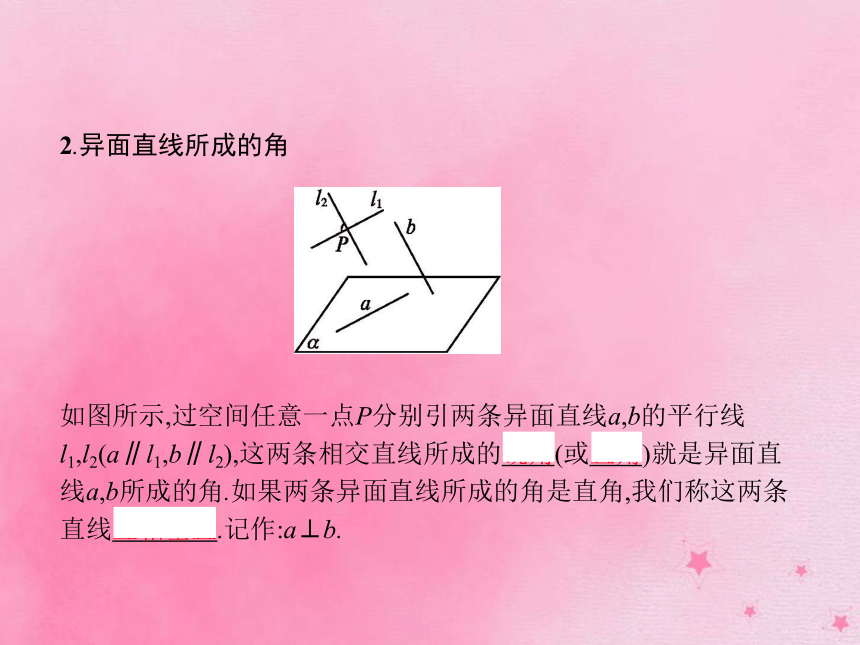
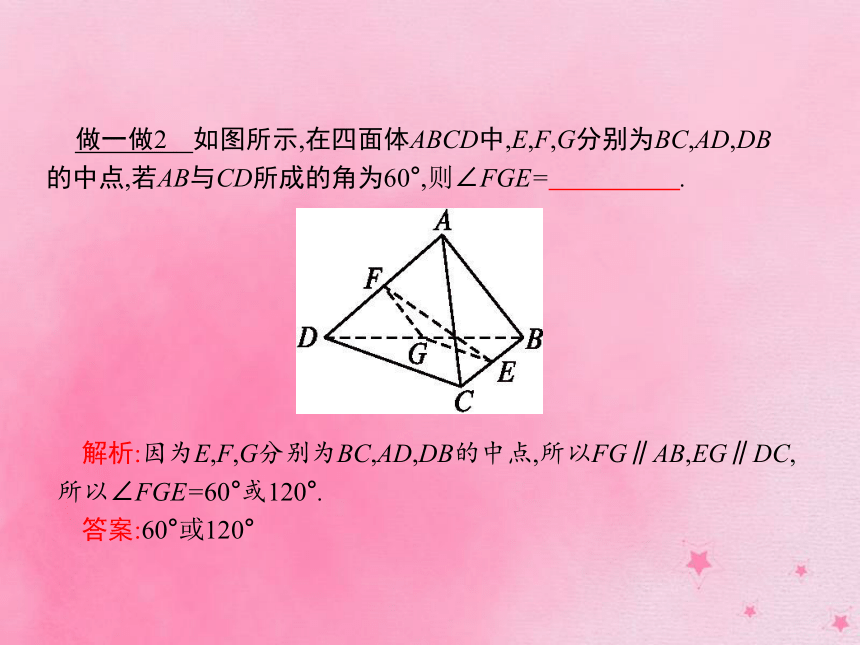
答案:A2.异面直线所成的角 如图所示,过空间任意一点P分别引两条异面直线a,b的平行线l1,l2(a∥l1,b∥l2),这两条相交直线所成的锐角(或直角)就是异面直线a,b所成的角.如果两条异面直线所成的角是直角,我们称这两条直线互相垂直.记作:a⊥b. 做一做2 如图所示,在四面体ABCD中,E,F,G分别为BC,AD,DB的中点,若AB与CD所成的角为60°,则∠FGE= .?解析:因为E,F,G分别为BC,AD,DB的中点,所以FG∥AB,EG∥DC,所以∠FGE=60°或120°.
答案:60°或120°3.空间四边形
四个顶点不在同一平面内的四边形叫作空间四边形.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若一个角的两边和另一个角的两边分别平行,且方向相同,则这两个角相等. ( )
(2)若一个角的两边和另一个角的两边分别平行,且有一组对边方向相同,另一组对边方向相反,则这两个角互补. ( )
(3)若一个角的两边和另一个角的两边分别平行,则这两个角相等. ( )
(4)若一个角的两边和另一个角的两边分别平行,且方向相反,则这两个角互补. ( )
(5)两条异面直线所成角的范围为[0°,90°). ( )√ √ × × × 探究一探究二一题多解 探究一等角定理的应用?
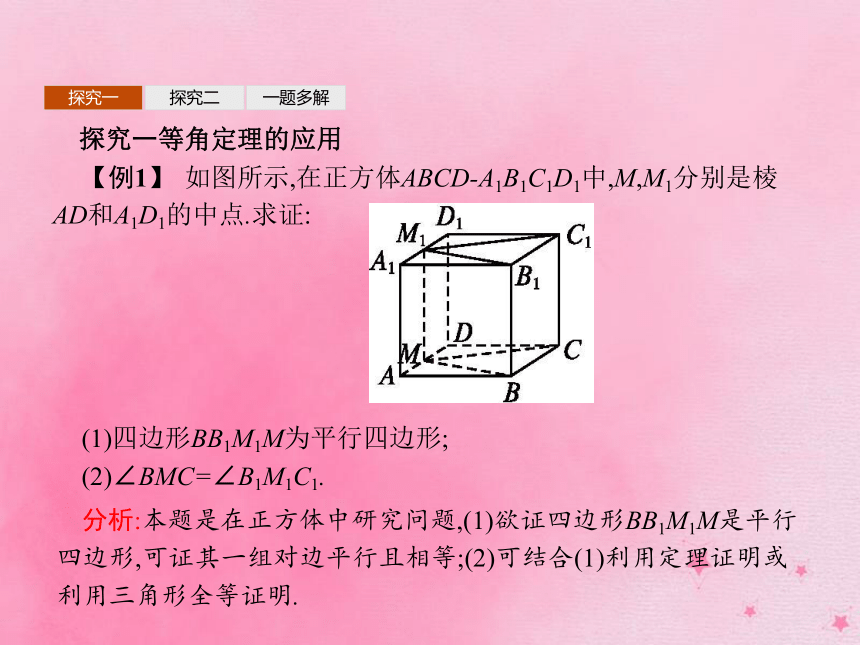
【例1】 如图所示,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:(1)四边形BB1M1M为平行四边形;
(2)∠BMC=∠B1M1C1.分析:本题是在正方体中研究问题,(1)欲证四边形BB1M1M是平行四边形,可证其一组对边平行且相等;(2)可结合(1)利用定理证明或利用三角形全等证明.探究一探究二一题多解证明:(1)在正方形ADD1A1中,∵M,M1分别为AD,A1D1的中点,∴MM1=AA1,MM1∥AA1.
又∵AA1=BB1,AA1∥BB1,
∴MM1=BB1,且MM1∥BB1.
∴四边形BB1M1M为平行四边形.
(2)方法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角,∴∠BMC=∠B1M1C1.探究一探究二一题多解方法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形.
∴C1M1=CM.
又B1C1=BC,∴△BCM≌△B1C1M1.
∴∠BMC=∠B1M1C1.
反思感悟1.要明确等角定理的两个条件,即两个角的两条边分别对应平行,并且方向相同,这两个条件缺一不可.
2.空间中证明两个角相等,可以利用等角定理,也可以利用三角形的相似或全等,还可以利用平行四边形的对角相等.在利用等角定理时,关键是弄清楚两个角对应边的关系.探究一探究二一题多解变式训练1在三棱柱ABC-A1B1C1中,M,N,P分别为边A1C1,AC和AB的中点.
求证:∠PNA1=∠BCM.
证明:因为P,N分别为AB,AC的中点,所以PN∥BC.①
又M,N分别为A1C1,AC的中点,所以A1M??NC.
所以四边形A1NCM为平行四边形,故A1N∥MC.②
由①②及∠PNA1与∠BCM对应边方向相同,得∠PNA1=∠BCM.探究一探究二一题多解探究二求两条异面直线所成的角
【例2】 如图所示,已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线BC'是异面直线?
(2)求异面直线AD'与B'C,BC'与CD'所成角的大小以及A'C与AB所成角的正切值.
分析:(1)按照异面直线的定义进行判断;(2)根据异面直线所成角的定义进行求解.探究一探究二一题多解解:(1)所在直线与BC'是异面直线的棱有:AA',DD',A'B',DC,AD,A'D'.
(2)因为AD'∥BC',所以AD'与B'C所成的角就是BC'与B'C所成的角.
因为BC'⊥B'C,所以AD'与B'C所成的角等于90°.
因为A'B∥CD',所以BC'与CD'所成的角就是BC'与A'B所成的角.
因为△A'C'B是等边三角形,所以∠A'BC'=60°,故BC'与CD'所成角的大小为60°.
因为AB∥CD,所以∠A'CD就是异面直线A'C与AB所成的角.
在△A'CD中,若设正方体的棱长为a,探究一探究二一题多解反思感悟求异面直线所成的角
1.求两条异面直线所成的角,一般是根据其定义求解,步骤如下:
(1)平移;(2)构造三角形;(3)解三角形;(4)作答.
2.在所给几何体中平移直线构造异面直线所成的角时,一般是选取其中一条直线上的特殊点,如顶点、棱的中点等.探究一探究二一题多解变式训练2如图所示,已知三棱锥A-BCD,AD=BC,E,F分别是AB,CD的中点,且EF= AD,求异面直线AD和BC所成角的大小.探究一探究二一题多解解:取AC的中点G,连接EG,FG.
因为E,F分别是AB,CD的中点, 由异面直线所成角的定义可知∠EGF或其补角即为异面直线AD,BC所成的角.所以异面直线AD和BC所成的角为90°. 探究一探究二一题多解【典例】 如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.
分析:要求异面直线所成角的大小,关键是作出异面直线所成的角,把它归结到三角形中,通过解三角形就可以得出答案.同时在解题时要注意异面直线所成角的范围.探究一探究二一题多解解法1(直接平移法)如图所示.
连接A1C1,B1D1交于点O,取DD1的中点G,
连接GA1,GC1,OG,则OG∥B1D,EF∥A1C1,故∠GOA1或其补角就是异面直线DB1与EF所成的角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.探究一探究二一题多解∴HF2=EF2+HE2,∴∠HEF=90°,
∴异面直线DB1与EF所成的角为90°.探究一探究二一题多解解法3如图所示,分别取AA1,CC1的中点M,N,连接MN,
则MN∥EF,所以直线MN与DB1所成的角就是异面直线DB1与EF所成的角.
连接MB1,DN,DM,B1N,则B1N∥DM,且B1N=DM,∴四边形DMB1N为平行四边形,
∴MN与B1D必相交,设交点为P.∴DM2=DP2+MP2,
∴∠DPM=90°,即DB1⊥EF,
∴异面直线DB1与EF所成的角为90°.探究一探究二一题多解解法4(补形法)如图所示,在原正方体的右侧补上一个同样的正方体,连接B1Q,DQ,则B1Q∥EF.
于是∠DB1Q或其补角就是异面直线DB1与EF所成的角,通过计算,不难得到B1D2+B1Q2=DQ2,故异面直线DB1与EF所成的角为90°.探究一探究二一题多解名师点评求两条异面直线所成角大小的步骤:(1)构造:选择适当的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊位置的点,如线段的端点或中点,也可以是异面直线中某一直线上的一个特殊点.(2)证明:证明作出的角就是要求的角.(3)计算:求角度,常利用三角形.(4)结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.123451.若∠AOB=∠A'O'B',OA∥O'A',且OA与O'A'的方向相同,则OB与O'B'( )
A.一定平行且方向相同 B.一定平行且方向相反
C.一定不平行 D.不一定平行
解析:由于两角不一定在同一个平面内或两角所在的平面不一定平行,因此OB与O'B'不一定平行.
答案:D123452.若一条直线与两条平行线中的一条为异面直线,则它与另一条( )
A.相交 B.异面
C.相交或异面 D.平行
解析:在如图所示的长方体ABCD-A1B1C1D1中,直线AA1与直线B1C1是异面直线,与B1C1平行的直线有A1D1,AD,BC,显然直线AA1与A1D1相交,与BC异面.
答案:C123453.在正方体ABCD-A1B1C1D1中,E,F,M分别为A1B1,B1C1,BB1的中点,下列说法错误的是( )
A.∠BA1C1=∠MEF
B.∠A1BC1=∠EMF
C.∠B1EM=∠EA1B
D.∠EFM=∠A1C1F
解析:由等角定理,可知A,B,C均正确.
答案:D123454.空间中,角A的两边和角B的两边分别平行,若∠A=70°,则∠B= .?
解析:因为角A的两边和角B的两边分别平行,
所以∠A=∠B或∠A+∠B=180°.
因为∠A=70°,所以∠B=70°或∠B=110°.
答案:70°或110°123455.如图所示,在空间四边形ABCD中,两条对边AB=CD=3,E,F分别是
和CD所成的角的大小.12345∴∠EMF(或其补角)为异面直线AB和CD所成的角.
∵AB=3,CD=3,∴EM=2,MF=1.
又EF= ,
∴MF2+EF2=EM2,∴∠MFE=90°,
∴∠EMF=60°,
∴异面直线AB和CD所成的角为60°.
空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补.名师点拨等角定理的符号语言与图形语言及作用.
(1)图形语言:如图①②所示.
(2)符号语言:已知OA∥O'A',OB∥O'B',则∠AOB=∠A'O'B'或∠AOB+∠A'O'B'=180°.
(3)作用:判断或证明两个角相等或互补.【做一做1】 空间两个角α,β的两边分别对应平行,且方向相同,若α=50°,则β等于( )
A.50° B.130°
C.40° D.50°或130°
解析:由等角定理知β与α相等.
答案:A2.异面直线所成的角 如图所示,过空间任意一点P分别引两条异面直线a,b的平行线l1,l2(a∥l1,b∥l2),这两条相交直线所成的锐角(或直角)就是异面直线a,b所成的角.如果两条异面直线所成的角是直角,我们称这两条直线互相垂直.记作:a⊥b. 做一做2 如图所示,在四面体ABCD中,E,F,G分别为BC,AD,DB的中点,若AB与CD所成的角为60°,则∠FGE= .?解析:因为E,F,G分别为BC,AD,DB的中点,所以FG∥AB,EG∥DC,所以∠FGE=60°或120°.
答案:60°或120°3.空间四边形
四个顶点不在同一平面内的四边形叫作空间四边形.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若一个角的两边和另一个角的两边分别平行,且方向相同,则这两个角相等. ( )
(2)若一个角的两边和另一个角的两边分别平行,且有一组对边方向相同,另一组对边方向相反,则这两个角互补. ( )
(3)若一个角的两边和另一个角的两边分别平行,则这两个角相等. ( )
(4)若一个角的两边和另一个角的两边分别平行,且方向相反,则这两个角互补. ( )
(5)两条异面直线所成角的范围为[0°,90°). ( )√ √ × × × 探究一探究二一题多解 探究一等角定理的应用?
【例1】 如图所示,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:(1)四边形BB1M1M为平行四边形;
(2)∠BMC=∠B1M1C1.分析:本题是在正方体中研究问题,(1)欲证四边形BB1M1M是平行四边形,可证其一组对边平行且相等;(2)可结合(1)利用定理证明或利用三角形全等证明.探究一探究二一题多解证明:(1)在正方形ADD1A1中,∵M,M1分别为AD,A1D1的中点,∴MM1=AA1,MM1∥AA1.
又∵AA1=BB1,AA1∥BB1,
∴MM1=BB1,且MM1∥BB1.
∴四边形BB1M1M为平行四边形.
(2)方法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角,∴∠BMC=∠B1M1C1.探究一探究二一题多解方法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形.
∴C1M1=CM.
又B1C1=BC,∴△BCM≌△B1C1M1.
∴∠BMC=∠B1M1C1.
反思感悟1.要明确等角定理的两个条件,即两个角的两条边分别对应平行,并且方向相同,这两个条件缺一不可.
2.空间中证明两个角相等,可以利用等角定理,也可以利用三角形的相似或全等,还可以利用平行四边形的对角相等.在利用等角定理时,关键是弄清楚两个角对应边的关系.探究一探究二一题多解变式训练1在三棱柱ABC-A1B1C1中,M,N,P分别为边A1C1,AC和AB的中点.
求证:∠PNA1=∠BCM.
证明:因为P,N分别为AB,AC的中点,所以PN∥BC.①
又M,N分别为A1C1,AC的中点,所以A1M??NC.
所以四边形A1NCM为平行四边形,故A1N∥MC.②
由①②及∠PNA1与∠BCM对应边方向相同,得∠PNA1=∠BCM.探究一探究二一题多解探究二求两条异面直线所成的角
【例2】 如图所示,已知正方体ABCD-A'B'C'D'.
(1)哪些棱所在的直线与直线BC'是异面直线?
(2)求异面直线AD'与B'C,BC'与CD'所成角的大小以及A'C与AB所成角的正切值.
分析:(1)按照异面直线的定义进行判断;(2)根据异面直线所成角的定义进行求解.探究一探究二一题多解解:(1)所在直线与BC'是异面直线的棱有:AA',DD',A'B',DC,AD,A'D'.
(2)因为AD'∥BC',所以AD'与B'C所成的角就是BC'与B'C所成的角.
因为BC'⊥B'C,所以AD'与B'C所成的角等于90°.
因为A'B∥CD',所以BC'与CD'所成的角就是BC'与A'B所成的角.
因为△A'C'B是等边三角形,所以∠A'BC'=60°,故BC'与CD'所成角的大小为60°.
因为AB∥CD,所以∠A'CD就是异面直线A'C与AB所成的角.
在△A'CD中,若设正方体的棱长为a,探究一探究二一题多解反思感悟求异面直线所成的角
1.求两条异面直线所成的角,一般是根据其定义求解,步骤如下:
(1)平移;(2)构造三角形;(3)解三角形;(4)作答.
2.在所给几何体中平移直线构造异面直线所成的角时,一般是选取其中一条直线上的特殊点,如顶点、棱的中点等.探究一探究二一题多解变式训练2如图所示,已知三棱锥A-BCD,AD=BC,E,F分别是AB,CD的中点,且EF= AD,求异面直线AD和BC所成角的大小.探究一探究二一题多解解:取AC的中点G,连接EG,FG.
因为E,F分别是AB,CD的中点, 由异面直线所成角的定义可知∠EGF或其补角即为异面直线AD,BC所成的角.所以异面直线AD和BC所成的角为90°. 探究一探究二一题多解【典例】 如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.
分析:要求异面直线所成角的大小,关键是作出异面直线所成的角,把它归结到三角形中,通过解三角形就可以得出答案.同时在解题时要注意异面直线所成角的范围.探究一探究二一题多解解法1(直接平移法)如图所示.
连接A1C1,B1D1交于点O,取DD1的中点G,
连接GA1,GC1,OG,则OG∥B1D,EF∥A1C1,故∠GOA1或其补角就是异面直线DB1与EF所成的角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.探究一探究二一题多解∴HF2=EF2+HE2,∴∠HEF=90°,
∴异面直线DB1与EF所成的角为90°.探究一探究二一题多解解法3如图所示,分别取AA1,CC1的中点M,N,连接MN,
则MN∥EF,所以直线MN与DB1所成的角就是异面直线DB1与EF所成的角.
连接MB1,DN,DM,B1N,则B1N∥DM,且B1N=DM,∴四边形DMB1N为平行四边形,
∴MN与B1D必相交,设交点为P.∴DM2=DP2+MP2,
∴∠DPM=90°,即DB1⊥EF,
∴异面直线DB1与EF所成的角为90°.探究一探究二一题多解解法4(补形法)如图所示,在原正方体的右侧补上一个同样的正方体,连接B1Q,DQ,则B1Q∥EF.
于是∠DB1Q或其补角就是异面直线DB1与EF所成的角,通过计算,不难得到B1D2+B1Q2=DQ2,故异面直线DB1与EF所成的角为90°.探究一探究二一题多解名师点评求两条异面直线所成角大小的步骤:(1)构造:选择适当的点,平移异面直线中的一条或两条成为相交直线,这里的点通常选择特殊位置的点,如线段的端点或中点,也可以是异面直线中某一直线上的一个特殊点.(2)证明:证明作出的角就是要求的角.(3)计算:求角度,常利用三角形.(4)结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.123451.若∠AOB=∠A'O'B',OA∥O'A',且OA与O'A'的方向相同,则OB与O'B'( )
A.一定平行且方向相同 B.一定平行且方向相反
C.一定不平行 D.不一定平行
解析:由于两角不一定在同一个平面内或两角所在的平面不一定平行,因此OB与O'B'不一定平行.
答案:D123452.若一条直线与两条平行线中的一条为异面直线,则它与另一条( )
A.相交 B.异面
C.相交或异面 D.平行
解析:在如图所示的长方体ABCD-A1B1C1D1中,直线AA1与直线B1C1是异面直线,与B1C1平行的直线有A1D1,AD,BC,显然直线AA1与A1D1相交,与BC异面.
答案:C123453.在正方体ABCD-A1B1C1D1中,E,F,M分别为A1B1,B1C1,BB1的中点,下列说法错误的是( )
A.∠BA1C1=∠MEF
B.∠A1BC1=∠EMF
C.∠B1EM=∠EA1B
D.∠EFM=∠A1C1F
解析:由等角定理,可知A,B,C均正确.
答案:D123454.空间中,角A的两边和角B的两边分别平行,若∠A=70°,则∠B= .?
解析:因为角A的两边和角B的两边分别平行,
所以∠A=∠B或∠A+∠B=180°.
因为∠A=70°,所以∠B=70°或∠B=110°.
答案:70°或110°123455.如图所示,在空间四边形ABCD中,两条对边AB=CD=3,E,F分别是
和CD所成的角的大小.12345∴∠EMF(或其补角)为异面直线AB和CD所成的角.
∵AB=3,CD=3,∴EM=2,MF=1.
又EF= ,
∴MF2+EF2=EM2,∴∠MFE=90°,
∴∠EMF=60°,
∴异面直线AB和CD所成的角为60°.
