2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.5.1平行关系的判定(26张)
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.5.1平行关系的判定(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 854.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 20:47:35 | ||
图片预览







文档简介
课件26张PPT。§5 平行关系5.1 平行关系的判定1.直线与平面平行的判定定理
(1)文字叙述:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
(2)符号表示:若直线l?平面α,直线b?α,l∥b,则l∥α.
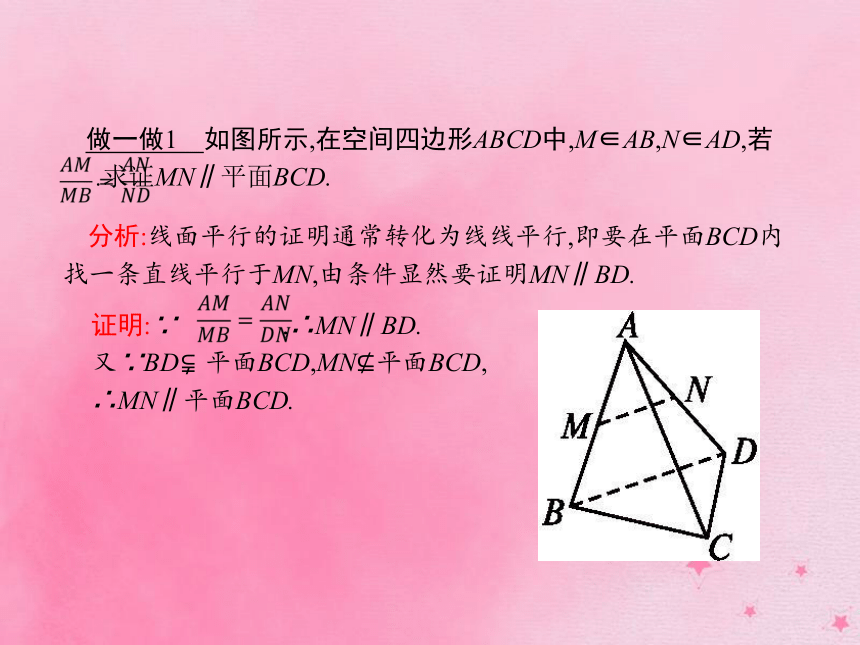
(3)图形表示:如图所示.(4)作用:线线平行?线面平行. 做一做1 如图所示,在空间四边形ABCD中,M∈AB,N∈AD,若
.求证MN∥平面BCD.?分析:线面平行的证明通常转化为线线平行,即要在平面BCD内找一条直线平行于MN,由条件显然要证明MN∥BD.证明:∵ ,∴MN∥BD.
又∵BD?平面BCD,MN?平面BCD,
∴MN∥平面BCD.2.平面与平面平行的判定定理
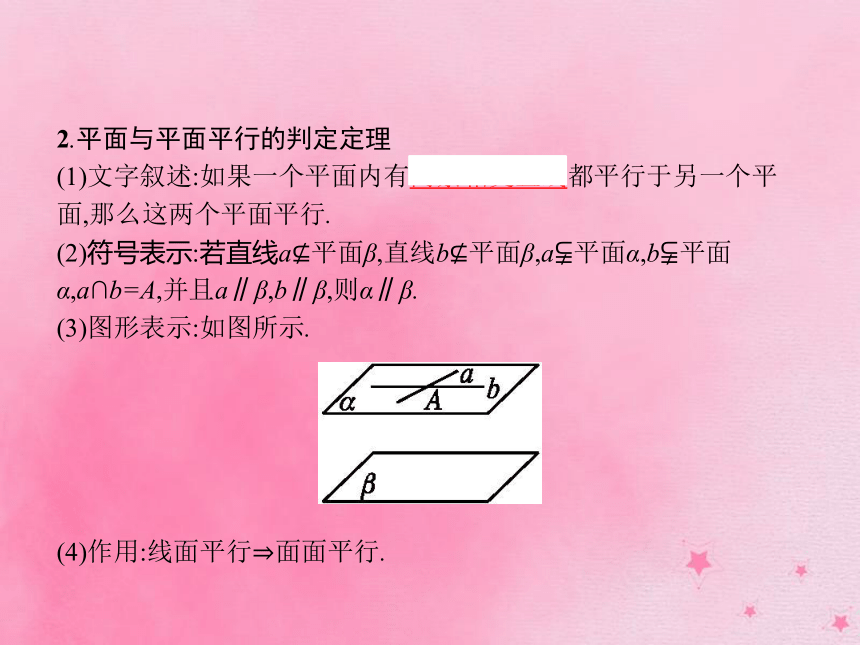
(1)文字叙述:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
(2)符号表示:若直线a?平面β,直线b?平面β,a?平面α,b?平面α,a∩b=A,并且a∥β,b∥β,则α∥β.
(3)图形表示:如图所示.(4)作用:线面平行?面面平行. 做一做2 若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )?
A.一定平行 B.一定相交
C.平行或相交 D.以上都不对
解析:当每个平面内的两条直线都是相交直线时,可推出两个平面一定平行,否则,两个平面有可能相交.
答案:C思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若直线a?平面α,直线b?平面β,且a∥b,则α∥β. ( )
(2)若直线a?平面α,直线b?平面β,且α∥β,则a,b无交点. ( )
(3)若直线a与平面α内无数条直线平行,则a∥α. ( )
(4)若平面α∥平面β,且a?α,b?β,则a∥b. ( )× √ × × 探究一探究二探究三探究一对线面平行、面面平行的理解
【例1】 判断下列说法是否正确.
(1)如果直线l与平面α不相交,那么l∥α;
(2)如果平面α内的任何一条直线都与平面β平行,那么α∥β;
(3)如果直线l∥α,l∥β,那么α∥β;
(4)如果直线l∥α,β∥α,那么l∥β.探究一探究二探究三解:(1)错误.当直线l与平面α不相交时,可以有l?α和l∥α两种情况,所以不一定有l∥α.
(2)正确.由于平面α内任何一条直线平行于平面β,可在平面α内选两条相交直线,则这两条相交直线都与平面β平行,由平面与平面平行的判定定理可得两个平面平行.
(3)错误.当l∥α,且l∥β时,可能有α∥β,但也可能有α与β相交,事实上,与两个相交平面的交线平行的直线与两个平面都是平行的.
(4)错误.当l∥α,β∥α时,不一定有l∥β,只有当l∥α,β∥α,且l?β时才能推出l∥β.探究一探究二探究三反思感悟1.在判断线面平行、面面平行时,两个判定定理是重要的依据,必须要对两个判定定理的条件做到全面、深刻的理解,忽视条件,容易导致判断错误.
2.明确空间直线与平面、平面与平面的位置关系的分类是解决问题的突破口,要充分考虑线面、面面关系中的各种情形,这类判断问题常用分类讨论的方法解决.另外,借助模型(如正方体、长方体等)也是解决这类问题的有效方法.再就是要善于列举反例来否定一个命题.探究一探究二探究三变式训练1已知直线l,m,平面α,β,下列命题正确的是( )
A.l∥β,l?α?α∥β
B.l∥β,m∥β,l?α,m?α?α∥β
C.l∥m,l?α,m?β?α∥β
D.l∥β,m∥β,l?α,m?α,l∩m=M?α∥β
解析:A,C错,α与β也可能相交;B错,只有当l,m相交时成立;根据面面平行的判定定理可知D正确.
答案:D探究一探究二探究三【例2】 如图所示,已知直棱柱ABCD-A1B1C1D1的底面是菱形,F为棱AA1的中点,M为线段BD1的中点,求证:MF∥平面ABCD.
分析:本题可在平面ABCD中找到一条与MF平行的直线来证明线面平行.探究二直线与平面平行的判定 探究一探究二探究三证法一连接AC,BD交于点O,再连接OM,如图所示,则OM∥D1D,且OM= D1D.
∵AF= A1A,AA1??DD1,
∴OM∥AF,且OM=AF,
∴四边形MOAF是平行四边形,∴MF∥OA.
又OA?平面ABCD,MF?平面ABCD,
∴MF∥平面ABCD.
证法二如图所示,连接D1F并延长交DA的延长线于点E,连接BE,
在△D1DE中,∵AF∥DD1,且AF= DD1,
∴F是D1E的中点,
∴FM是△BED1的中位线,∴FM∥BE.
∵BE?平面ABCD,MF?平面ABCD,
∴MF∥平面ABCD.探究一探究二探究三反思感悟1.证明线面平行的关键是证明线线平行,通常利用平行四边形、中位线、平行公理等来证明,辅助线要根据题中所给点的位置关系来确定.
2.直线与平面平行的判定定理的应用步骤其中,在平面α内的直线是关键,它要么是已经存在,需要被发现或找到,要么是在图形中还未出现,需要作出.探究一探究二探究三变式训练2如图所示,P是平行四边形ABCD所在平面外一点,Q是PA的中点,试判断PC与平面BDQ的关系,并证明.解:PC∥平面BDQ.
证明如下:如图所示,连接AC,交BD于点O,连接OQ.
∵四边形ABCD是平行四边形,
∴O为AC的中点.
又Q是PA的中点,
∴OQ∥PC.
又PC?平面BDQ,OQ?平面BDQ,∴PC∥平面BDQ.探究一探究二探究三【例3】如图所示,在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CD1B1.
分析:根据面面平行的判定定理,只要在其中一个平面内找到两条相交直线平行于另外一个平面即可.
证明:∵B1B??A1A,A1A??D1D,
∴B1B??D1D.
∴四边形BB1D1D是平行四边形,
∴D1B1∥DB.
又DB?平面A1BD,D1B1?平面A1BD,
∴D1B1∥平面A1BD,同理B1C∥平面A1BD,
而B1C?平面CD1B1,B1D1?平面CD1B1,D1B1∩B1C=B1,
∴平面A1BD∥平面CD1B1.探究三面面平行的判定 探究一探究二探究三反思感悟怎样证明平面与平面平行
证明两个平面平行的方法有:(1)用两个平面平行的定义,此类题目常用反证法来完成;(2)用判定定理,通过证明线面平行来完成.要证面面平行,依据判定定理只需找出一个平面内的两条相交直线分别平行于另一个平面即可.另外,在证明线线、线面以及面面平行时,常进行如下转化:线线平行 线面平行 面面平行.探究一探究二探究三变式训练3在底面是平行四边形的四棱锥P-ABCD中,点E在PD上,且PE∶ED=2∶1,M为PE的中点,在棱PC上是否存在一点F,使平面BFM∥平面AEC?并证明你的结论.探究一探究二探究三解:当F是棱PC的中点时,平面BFM∥平面AEC.
∵M是PE的中点,∴FM∥CE.
∵FM?平面AEC,CE?平面AEC,
∴FM∥平面AEC.由EM= PE=ED,
得E为MD的中点,连接BM,BD,如图所示,
设BD∩AC=O,则O为BD的中点.
连接OE,则BM∥OE.
∵BM?平面AEC,OE?平面AEC,
∴BM∥平面AEC.
∵FM?平面BFM,BM?平面BFM,FM∩BM=M,
∴平面BFM∥平面AEC.123451.根据下列条件,能得到直线a∥平面α的是( )
A.a?α
B.a∥b,b?α
C.a与平面α没有公共点
D.a上有不同的两点到平面α的距离相等
答案:C123452.已知a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,给出的下列命题中,正确的个数为( )A.1 B.2
C.3 D.4
解析:①④正确.
答案:B123453.在六棱柱的表面中,互相平行的面最多有 对.?
答案:4123454.如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,E,F分别为棱PB,PC的中点,则EF与平面PAD的位置关系为 .?
解析:因为E,F分别是PB,PC的中点,所以EF∥BC.
又AD∥BC,所以EF∥AD.
而EF?平面PAD,AD?平面PAD,
故EF∥平面PAD.
答案:EF∥平面PAD123455.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC,SC的中点,求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面 BDD1B1.12345证明:(1)如图所示,连接SB,
∵E,G分别是BC,SC的中点,∴EG∥SB.
又SB?平面BDD1B1,
EG?平面BDD1B1,
∴直线EG∥平面BDD1B1.
(2)连接SD,
∵F,G分别是DC,SC的中点,∴FG∥SD.
又SD?平面BDD1B1,FG?平面BDD1B1,
∴FG∥平面BDD1B1.
又EG?平面EFG,
FG?平面EFG,EG∩FG=G,
∴平面EFG∥平面BDD1B1.
(1)文字叙述:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
(2)符号表示:若直线l?平面α,直线b?α,l∥b,则l∥α.
(3)图形表示:如图所示.(4)作用:线线平行?线面平行. 做一做1 如图所示,在空间四边形ABCD中,M∈AB,N∈AD,若
.求证MN∥平面BCD.?分析:线面平行的证明通常转化为线线平行,即要在平面BCD内找一条直线平行于MN,由条件显然要证明MN∥BD.证明:∵ ,∴MN∥BD.
又∵BD?平面BCD,MN?平面BCD,
∴MN∥平面BCD.2.平面与平面平行的判定定理
(1)文字叙述:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
(2)符号表示:若直线a?平面β,直线b?平面β,a?平面α,b?平面α,a∩b=A,并且a∥β,b∥β,则α∥β.
(3)图形表示:如图所示.(4)作用:线面平行?面面平行. 做一做2 若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )?
A.一定平行 B.一定相交
C.平行或相交 D.以上都不对
解析:当每个平面内的两条直线都是相交直线时,可推出两个平面一定平行,否则,两个平面有可能相交.
答案:C思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若直线a?平面α,直线b?平面β,且a∥b,则α∥β. ( )
(2)若直线a?平面α,直线b?平面β,且α∥β,则a,b无交点. ( )
(3)若直线a与平面α内无数条直线平行,则a∥α. ( )
(4)若平面α∥平面β,且a?α,b?β,则a∥b. ( )× √ × × 探究一探究二探究三探究一对线面平行、面面平行的理解
【例1】 判断下列说法是否正确.
(1)如果直线l与平面α不相交,那么l∥α;
(2)如果平面α内的任何一条直线都与平面β平行,那么α∥β;
(3)如果直线l∥α,l∥β,那么α∥β;
(4)如果直线l∥α,β∥α,那么l∥β.探究一探究二探究三解:(1)错误.当直线l与平面α不相交时,可以有l?α和l∥α两种情况,所以不一定有l∥α.
(2)正确.由于平面α内任何一条直线平行于平面β,可在平面α内选两条相交直线,则这两条相交直线都与平面β平行,由平面与平面平行的判定定理可得两个平面平行.
(3)错误.当l∥α,且l∥β时,可能有α∥β,但也可能有α与β相交,事实上,与两个相交平面的交线平行的直线与两个平面都是平行的.
(4)错误.当l∥α,β∥α时,不一定有l∥β,只有当l∥α,β∥α,且l?β时才能推出l∥β.探究一探究二探究三反思感悟1.在判断线面平行、面面平行时,两个判定定理是重要的依据,必须要对两个判定定理的条件做到全面、深刻的理解,忽视条件,容易导致判断错误.
2.明确空间直线与平面、平面与平面的位置关系的分类是解决问题的突破口,要充分考虑线面、面面关系中的各种情形,这类判断问题常用分类讨论的方法解决.另外,借助模型(如正方体、长方体等)也是解决这类问题的有效方法.再就是要善于列举反例来否定一个命题.探究一探究二探究三变式训练1已知直线l,m,平面α,β,下列命题正确的是( )
A.l∥β,l?α?α∥β
B.l∥β,m∥β,l?α,m?α?α∥β
C.l∥m,l?α,m?β?α∥β
D.l∥β,m∥β,l?α,m?α,l∩m=M?α∥β
解析:A,C错,α与β也可能相交;B错,只有当l,m相交时成立;根据面面平行的判定定理可知D正确.
答案:D探究一探究二探究三【例2】 如图所示,已知直棱柱ABCD-A1B1C1D1的底面是菱形,F为棱AA1的中点,M为线段BD1的中点,求证:MF∥平面ABCD.
分析:本题可在平面ABCD中找到一条与MF平行的直线来证明线面平行.探究二直线与平面平行的判定 探究一探究二探究三证法一连接AC,BD交于点O,再连接OM,如图所示,则OM∥D1D,且OM= D1D.
∵AF= A1A,AA1??DD1,
∴OM∥AF,且OM=AF,
∴四边形MOAF是平行四边形,∴MF∥OA.
又OA?平面ABCD,MF?平面ABCD,
∴MF∥平面ABCD.
证法二如图所示,连接D1F并延长交DA的延长线于点E,连接BE,
在△D1DE中,∵AF∥DD1,且AF= DD1,
∴F是D1E的中点,
∴FM是△BED1的中位线,∴FM∥BE.
∵BE?平面ABCD,MF?平面ABCD,
∴MF∥平面ABCD.探究一探究二探究三反思感悟1.证明线面平行的关键是证明线线平行,通常利用平行四边形、中位线、平行公理等来证明,辅助线要根据题中所给点的位置关系来确定.
2.直线与平面平行的判定定理的应用步骤其中,在平面α内的直线是关键,它要么是已经存在,需要被发现或找到,要么是在图形中还未出现,需要作出.探究一探究二探究三变式训练2如图所示,P是平行四边形ABCD所在平面外一点,Q是PA的中点,试判断PC与平面BDQ的关系,并证明.解:PC∥平面BDQ.
证明如下:如图所示,连接AC,交BD于点O,连接OQ.
∵四边形ABCD是平行四边形,
∴O为AC的中点.
又Q是PA的中点,
∴OQ∥PC.
又PC?平面BDQ,OQ?平面BDQ,∴PC∥平面BDQ.探究一探究二探究三【例3】如图所示,在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CD1B1.
分析:根据面面平行的判定定理,只要在其中一个平面内找到两条相交直线平行于另外一个平面即可.
证明:∵B1B??A1A,A1A??D1D,
∴B1B??D1D.
∴四边形BB1D1D是平行四边形,
∴D1B1∥DB.
又DB?平面A1BD,D1B1?平面A1BD,
∴D1B1∥平面A1BD,同理B1C∥平面A1BD,
而B1C?平面CD1B1,B1D1?平面CD1B1,D1B1∩B1C=B1,
∴平面A1BD∥平面CD1B1.探究三面面平行的判定 探究一探究二探究三反思感悟怎样证明平面与平面平行
证明两个平面平行的方法有:(1)用两个平面平行的定义,此类题目常用反证法来完成;(2)用判定定理,通过证明线面平行来完成.要证面面平行,依据判定定理只需找出一个平面内的两条相交直线分别平行于另一个平面即可.另外,在证明线线、线面以及面面平行时,常进行如下转化:线线平行 线面平行 面面平行.探究一探究二探究三变式训练3在底面是平行四边形的四棱锥P-ABCD中,点E在PD上,且PE∶ED=2∶1,M为PE的中点,在棱PC上是否存在一点F,使平面BFM∥平面AEC?并证明你的结论.探究一探究二探究三解:当F是棱PC的中点时,平面BFM∥平面AEC.
∵M是PE的中点,∴FM∥CE.
∵FM?平面AEC,CE?平面AEC,
∴FM∥平面AEC.由EM= PE=ED,
得E为MD的中点,连接BM,BD,如图所示,
设BD∩AC=O,则O为BD的中点.
连接OE,则BM∥OE.
∵BM?平面AEC,OE?平面AEC,
∴BM∥平面AEC.
∵FM?平面BFM,BM?平面BFM,FM∩BM=M,
∴平面BFM∥平面AEC.123451.根据下列条件,能得到直线a∥平面α的是( )
A.a?α
B.a∥b,b?α
C.a与平面α没有公共点
D.a上有不同的两点到平面α的距离相等
答案:C123452.已知a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,给出的下列命题中,正确的个数为( )A.1 B.2
C.3 D.4
解析:①④正确.
答案:B123453.在六棱柱的表面中,互相平行的面最多有 对.?
答案:4123454.如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,E,F分别为棱PB,PC的中点,则EF与平面PAD的位置关系为 .?
解析:因为E,F分别是PB,PC的中点,所以EF∥BC.
又AD∥BC,所以EF∥AD.
而EF?平面PAD,AD?平面PAD,
故EF∥平面PAD.
答案:EF∥平面PAD123455.如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC,SC的中点,求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面 BDD1B1.12345证明:(1)如图所示,连接SB,
∵E,G分别是BC,SC的中点,∴EG∥SB.
又SB?平面BDD1B1,
EG?平面BDD1B1,
∴直线EG∥平面BDD1B1.
(2)连接SD,
∵F,G分别是DC,SC的中点,∴FG∥SD.
又SD?平面BDD1B1,FG?平面BDD1B1,
∴FG∥平面BDD1B1.
又EG?平面EFG,
FG?平面EFG,EG∩FG=G,
∴平面EFG∥平面BDD1B1.
