2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.5.2平行关系的性质(24张)
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.5.2平行关系的性质(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 20:48:32 | ||
图片预览







文档简介
课件24张PPT。5.2 平行关系的性质1.直线与平面平行的性质定理
文字语言:如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.
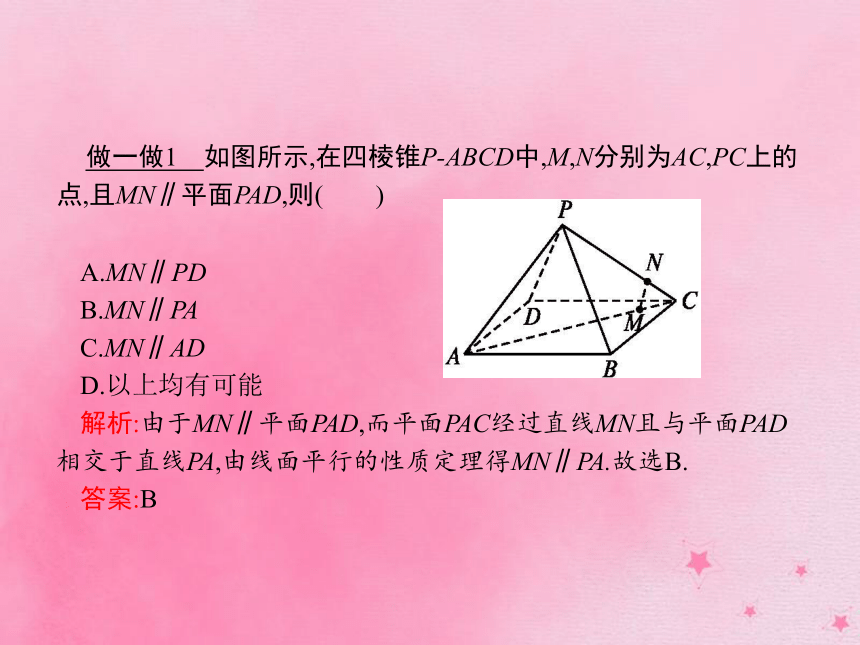
符号语言:l∥α,l?β,α∩β=b?l∥b.图形语言: 作用:证明两条直线平行. 做一做1 如图所示,在四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )?A.MN∥PD
B.MN∥PA
C.MN∥AD
D.以上均有可能
解析:由于MN∥平面PAD,而平面PAC经过直线MN且与平面PAD相交于直线PA,由线面平行的性质定理得MN∥PA.故选B.
答案:B名师点拨正确理解线面平行的性质定理:
(1)直线与平面平行的性质定理中有三个条件:①直线l和平面α平行,即l∥α;②平面α,β相交,即α∩β=b;③直线l在平面β内,即l?β.这三个条件缺一不可.
(2)线面平行的性质定理可以作为证明线线平行的一种方法.
(3)在应用线面平行的性质定理时,往往会出现这样的易错点:“a∥β,b?β,所以a∥b”,所以在应用时要谨慎.
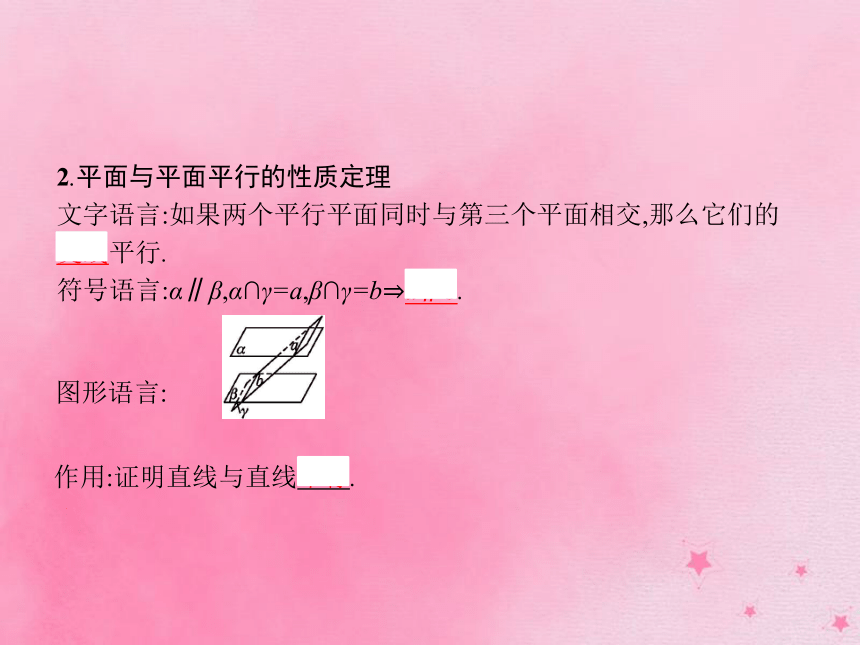
(4)线面平行的判定定理与性质定理常常交替使用:先通过线线平行找出线面平行,再通过线面平行推出线线平行,其关系可用以下关系链表示:2.平面与平面平行的性质定理
文字语言:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
符号语言:α∥β,α∩γ=a,β∩γ=b?a∥b.图形语言: 作用:证明直线与直线平行. 做一做2 平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是 ( )?
A.互相平行 B.交于一点
C.相互异面 D.不能确定
解析:由面面平行的性质定理,可知答案为A.
答案:A名师点拨正确理解面面平行的性质定理:
(1)面面平行的性质定理可以作为证明线线平行的一种方法.
(2)已知两个平面平行,虽然一个平面内的任何直线都平行于另一个平面,但是这两个平面内的所有直线并不一定相互平行.
(3)面面平行的其他性质:
①在两个平行平面中,一个平面内的直线必平行于另一个平面.简言之:“面面平行,则线面平行.”这可以作为证明线面平行的一种方法.
②夹在两个平行平面间的平行线段相等.
③如果两个平面都与第三个平面平行,那么这两个平面互相平行.
④两条直线被三个平行平面所截,截得的对应线段成比例.
⑤经过平面外一点有且只有一个平面与已知平面平行.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若三个平面α,β,γ满足α∥β∥γ,且平面δ与这三个平面相交,交线分别为a,b,c,则有a∥b∥c成立. ( )
(2)若直线a与平面α不平行,过直线a的平面β与平面α的交线为l,则a与l不平行. ( )
(3)若直线a与平面α平行,则直线a一定平行于平面α内所有的直线. ( )√ √ × 探究一探究二易错辨析探究一直线与平面平行的性质及其应用
【例1】 如图,用平行于四面体ABCD的一组对棱AB,CD的平面截此四面体.求证:截面MNPQ是平行四边形.
分析:根据已知AB∥平面MNPQ,CD∥平面MNPQ,根据线面平行的性质定理,找出经过直线的平面与平面MNPQ的交线,转化为线线平行即可得证.
证明因为AB∥平面MNPQ,平面ABC∩平面MNPQ=MN,且AB?平面ABC,
所以由线面平行的性质定理,知AB∥MN.
同理,AB∥PQ,
所以MN∥PQ.同理,可得MQ∥NP.
所以截面MNPQ是平行四边形.探究一探究二易错辨析反思感悟(1)利用线面平行的性质定理解题的步骤
(2)运用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与这个平面相交的交线,然后确定线线平行.探究一探究二易错辨析延伸探究2若本例中添加条件:AB⊥CD,AB=10,CD=8,且BP∶PD=1∶1,求四边形MNPQ的面积.
解:由例1知,四边形MNPQ是平行四边形,
∵AB⊥CD,∴PQ⊥QM,
∴四边形MNPQ是矩形.
∵BP∶PD=1∶1,
∴PQ=5,QM=4,
∴四边形MNPQ的面积为5×4=20.探究一探究二易错辨析探究二平面与平面平行的性质及其应用
【例2】 如图所示,在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1.若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1?并证明你的结论.
分析:先找出过DE与平面AB1C1平行的平面,可直接找出过D、E与△AB1C1的三边平行的直线,进而确定平面,然后确定其与棱AB的交点,即可找出E点位置,然后利用定理进行证明即可.探究一探究二易错辨析解:当E为棱AB的中点时,DE∥平面AB1C1.
证明如下:
如图所示,取BB1的中点F,连接EF,FD,DE.
因为D,E,F分别为CC1,AB,BB1的中点,
所以EF∥AB1.
因为AB1?平面AB1C1,EF?平面AB1C1,
所以EF∥平面AB1C1.同理可证FD∥平面AB1C1.
因为EF∩FD=F,所以平面EFD∥平面AB1C1.
因为DE?平面EFD,所以DE∥平面AB1C1.探究一探究二易错辨析延伸探究若在△ABC内找一点E呢?点E只有一个吗?若只有一个,确定点E的位置;若不是,试写出点E的集合.
解:能找到.点E有无数个,点E的集合是线段PQ.
如图,取棱AB的中点P,棱AC的中点Q,BB1的中点F.连接PD,PF,DF,PQ,QD.
在△ABC中,P,Q分别是AB,AC的中点,
所以PQ∥BC.
在?CBB1C1中,因为D,F分别为CC1,BB1的中点,
所以DF∥B1C1,
所以PQ∥DF,故四边形PQDF是一个梯形.
又DF∥B1C1,DF?平面AB1C1,B1C1?平面AB1C1,
所以DF∥平面AB1C1.
同理,PF∥平面AB1C1.探究一探究二易错辨析又PF∩DF=F,所以平面PQDF∥平面AB1C1.
故点E的集合是线段PQ.探究一探究二易错辨析在立体几何证明中错套平面几何定理而致误
【典例】 如图所示,已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1,CC1的中点.求证:四边形BED1F是平行四边形.
错解在正方体ABCD-A1B1C1D1中,平面A1ADD1∥平面B1BCC1,
由面面平行的性质定理得D1E∥FB,
同理,D1F∥EB,故四边形EBFD1为平行四边形.探究一探究二易错辨析正解取D1D的中点G,连接EG,GC,
∵E是A1A的中点,G是D1D的中点,∴EG??AD.
由正方体性质知AD??BC,∴EG??BC.
∴四边形EGCB是平行四边形,∴EB??GC.①
又∵G,F分别是D1D,C1C的中点,∴D1G??FC.
∴四边形D1GCF为平行四边形,∴D1F??GC.②
由①②知EB??D1F,∴四边形BED1F是平行四边形.
纠错心得1.立体几何问题只有在转化为平面几何问题后才能直接使用平面几何知识解决,正确的解题思路是将立体几何问题转化为平面几何问题再证明.
2.错解中就是想当然认为四边形BED1F是平面图形,而没有必要的说理.123451.若直线a平行于平面α,则下列说法正确的是( )
A.平面α内有且只有一条直线与a平行
B.平面α内有无数条直线与a平行
C.平面α内不存在与a平行的直线
D.平面α内任一条直线都与a平行
答案:B123452.若平面α∥平面β,a?α,b?β,则a与b一定是( )
A.平行直线 B.异面直线
C.相交直线 D.无公共点的直线答案:D 123453.如图,a∥α,A是α的另一侧的点,B,C,D∈a,线段AB,AC,AD分别交平面α于E,F,G,若BD=4,CF=4,AF=5,则EG= .?123454.如图所示,在三棱锥A-BCD中,AB=CD=a,截面EFGH与AB,CD都平行,则截面EFGH的周长是 .?所以截面EFGH的周长为2a.
答案:2a123455.在正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1与BC的中点,求证:EF∥平面A1ACC1.12345证明:取B1C1的中点G,连接EG,GF.
因为E,G分别是A1B1,B1C1的中点,
所以EG∥A1C1.
因为EG?平面A1ACC1,A1C1?平面A1ACC1,
所以EG∥平面 A1ACC1.
同理,因为G,F分别是B1C1,BC的中点,
所以GF∥C1C.
因为GF?平面A1ACC1,C1C?平面A1ACC1,
所以GF∥平面A1ACC1.
因为EG∩GF=G,所以平面EFG∥平面A1ACC1.
又EF?平面EFG,所以EF∥平面A1ACC1.
文字语言:如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.
符号语言:l∥α,l?β,α∩β=b?l∥b.图形语言: 作用:证明两条直线平行. 做一做1 如图所示,在四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )?A.MN∥PD
B.MN∥PA
C.MN∥AD
D.以上均有可能
解析:由于MN∥平面PAD,而平面PAC经过直线MN且与平面PAD相交于直线PA,由线面平行的性质定理得MN∥PA.故选B.
答案:B名师点拨正确理解线面平行的性质定理:
(1)直线与平面平行的性质定理中有三个条件:①直线l和平面α平行,即l∥α;②平面α,β相交,即α∩β=b;③直线l在平面β内,即l?β.这三个条件缺一不可.
(2)线面平行的性质定理可以作为证明线线平行的一种方法.
(3)在应用线面平行的性质定理时,往往会出现这样的易错点:“a∥β,b?β,所以a∥b”,所以在应用时要谨慎.
(4)线面平行的判定定理与性质定理常常交替使用:先通过线线平行找出线面平行,再通过线面平行推出线线平行,其关系可用以下关系链表示:2.平面与平面平行的性质定理
文字语言:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
符号语言:α∥β,α∩γ=a,β∩γ=b?a∥b.图形语言: 作用:证明直线与直线平行. 做一做2 平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是 ( )?
A.互相平行 B.交于一点
C.相互异面 D.不能确定
解析:由面面平行的性质定理,可知答案为A.
答案:A名师点拨正确理解面面平行的性质定理:
(1)面面平行的性质定理可以作为证明线线平行的一种方法.
(2)已知两个平面平行,虽然一个平面内的任何直线都平行于另一个平面,但是这两个平面内的所有直线并不一定相互平行.
(3)面面平行的其他性质:
①在两个平行平面中,一个平面内的直线必平行于另一个平面.简言之:“面面平行,则线面平行.”这可以作为证明线面平行的一种方法.
②夹在两个平行平面间的平行线段相等.
③如果两个平面都与第三个平面平行,那么这两个平面互相平行.
④两条直线被三个平行平面所截,截得的对应线段成比例.
⑤经过平面外一点有且只有一个平面与已知平面平行.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若三个平面α,β,γ满足α∥β∥γ,且平面δ与这三个平面相交,交线分别为a,b,c,则有a∥b∥c成立. ( )
(2)若直线a与平面α不平行,过直线a的平面β与平面α的交线为l,则a与l不平行. ( )
(3)若直线a与平面α平行,则直线a一定平行于平面α内所有的直线. ( )√ √ × 探究一探究二易错辨析探究一直线与平面平行的性质及其应用
【例1】 如图,用平行于四面体ABCD的一组对棱AB,CD的平面截此四面体.求证:截面MNPQ是平行四边形.
分析:根据已知AB∥平面MNPQ,CD∥平面MNPQ,根据线面平行的性质定理,找出经过直线的平面与平面MNPQ的交线,转化为线线平行即可得证.
证明因为AB∥平面MNPQ,平面ABC∩平面MNPQ=MN,且AB?平面ABC,
所以由线面平行的性质定理,知AB∥MN.
同理,AB∥PQ,
所以MN∥PQ.同理,可得MQ∥NP.
所以截面MNPQ是平行四边形.探究一探究二易错辨析反思感悟(1)利用线面平行的性质定理解题的步骤
(2)运用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与这个平面相交的交线,然后确定线线平行.探究一探究二易错辨析延伸探究2若本例中添加条件:AB⊥CD,AB=10,CD=8,且BP∶PD=1∶1,求四边形MNPQ的面积.
解:由例1知,四边形MNPQ是平行四边形,
∵AB⊥CD,∴PQ⊥QM,
∴四边形MNPQ是矩形.
∵BP∶PD=1∶1,
∴PQ=5,QM=4,
∴四边形MNPQ的面积为5×4=20.探究一探究二易错辨析探究二平面与平面平行的性质及其应用
【例2】 如图所示,在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1.若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1?并证明你的结论.
分析:先找出过DE与平面AB1C1平行的平面,可直接找出过D、E与△AB1C1的三边平行的直线,进而确定平面,然后确定其与棱AB的交点,即可找出E点位置,然后利用定理进行证明即可.探究一探究二易错辨析解:当E为棱AB的中点时,DE∥平面AB1C1.
证明如下:
如图所示,取BB1的中点F,连接EF,FD,DE.
因为D,E,F分别为CC1,AB,BB1的中点,
所以EF∥AB1.
因为AB1?平面AB1C1,EF?平面AB1C1,
所以EF∥平面AB1C1.同理可证FD∥平面AB1C1.
因为EF∩FD=F,所以平面EFD∥平面AB1C1.
因为DE?平面EFD,所以DE∥平面AB1C1.探究一探究二易错辨析延伸探究若在△ABC内找一点E呢?点E只有一个吗?若只有一个,确定点E的位置;若不是,试写出点E的集合.
解:能找到.点E有无数个,点E的集合是线段PQ.
如图,取棱AB的中点P,棱AC的中点Q,BB1的中点F.连接PD,PF,DF,PQ,QD.
在△ABC中,P,Q分别是AB,AC的中点,
所以PQ∥BC.
在?CBB1C1中,因为D,F分别为CC1,BB1的中点,
所以DF∥B1C1,
所以PQ∥DF,故四边形PQDF是一个梯形.
又DF∥B1C1,DF?平面AB1C1,B1C1?平面AB1C1,
所以DF∥平面AB1C1.
同理,PF∥平面AB1C1.探究一探究二易错辨析又PF∩DF=F,所以平面PQDF∥平面AB1C1.
故点E的集合是线段PQ.探究一探究二易错辨析在立体几何证明中错套平面几何定理而致误
【典例】 如图所示,已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1,CC1的中点.求证:四边形BED1F是平行四边形.
错解在正方体ABCD-A1B1C1D1中,平面A1ADD1∥平面B1BCC1,
由面面平行的性质定理得D1E∥FB,
同理,D1F∥EB,故四边形EBFD1为平行四边形.探究一探究二易错辨析正解取D1D的中点G,连接EG,GC,
∵E是A1A的中点,G是D1D的中点,∴EG??AD.
由正方体性质知AD??BC,∴EG??BC.
∴四边形EGCB是平行四边形,∴EB??GC.①
又∵G,F分别是D1D,C1C的中点,∴D1G??FC.
∴四边形D1GCF为平行四边形,∴D1F??GC.②
由①②知EB??D1F,∴四边形BED1F是平行四边形.
纠错心得1.立体几何问题只有在转化为平面几何问题后才能直接使用平面几何知识解决,正确的解题思路是将立体几何问题转化为平面几何问题再证明.
2.错解中就是想当然认为四边形BED1F是平面图形,而没有必要的说理.123451.若直线a平行于平面α,则下列说法正确的是( )
A.平面α内有且只有一条直线与a平行
B.平面α内有无数条直线与a平行
C.平面α内不存在与a平行的直线
D.平面α内任一条直线都与a平行
答案:B123452.若平面α∥平面β,a?α,b?β,则a与b一定是( )
A.平行直线 B.异面直线
C.相交直线 D.无公共点的直线答案:D 123453.如图,a∥α,A是α的另一侧的点,B,C,D∈a,线段AB,AC,AD分别交平面α于E,F,G,若BD=4,CF=4,AF=5,则EG= .?123454.如图所示,在三棱锥A-BCD中,AB=CD=a,截面EFGH与AB,CD都平行,则截面EFGH的周长是 .?所以截面EFGH的周长为2a.
答案:2a123455.在正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1与BC的中点,求证:EF∥平面A1ACC1.12345证明:取B1C1的中点G,连接EG,GF.
因为E,G分别是A1B1,B1C1的中点,
所以EG∥A1C1.
因为EG?平面A1ACC1,A1C1?平面A1ACC1,
所以EG∥平面 A1ACC1.
同理,因为G,F分别是B1C1,BC的中点,
所以GF∥C1C.
因为GF?平面A1ACC1,C1C?平面A1ACC1,
所以GF∥平面A1ACC1.
因为EG∩GF=G,所以平面EFG∥平面A1ACC1.
又EF?平面EFG,所以EF∥平面A1ACC1.
