2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.6.1垂直关系的判定(32张)
文档属性
| 名称 | 2019-2020学年高中数学北师大版必修2课件:第一章立体几何初步1.6.1垂直关系的判定(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览











文档简介
课件32张PPT。§6 垂直关系6.1 垂直关系的判定1.直线与平面垂直
(1)直线与平面垂直的定义
如果一条直线和一个平面内的任何一条直线都垂直,那么称这条直线和这个平面垂直.
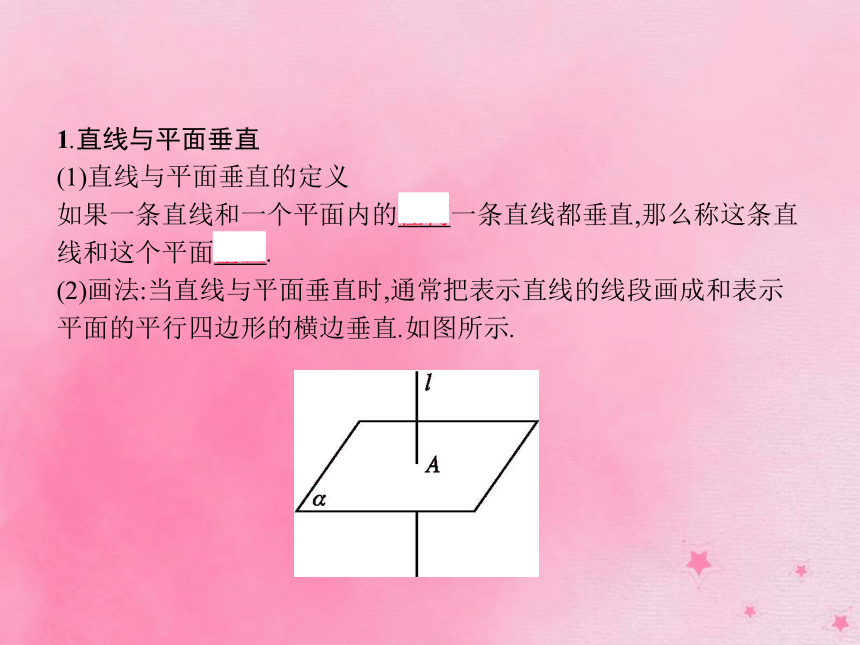
(2)画法:当直线与平面垂直时,通常把表示直线的线段画成和表示平面的平行四边形的横边垂直.如图所示.(3)直线与平面垂直的判定定理
①文字叙述:如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
②符号表示:若直线a?α,直线b?α,直线l⊥a,l⊥b,a∩b=A,则l⊥α.③图形表示: ④作用:线线垂直?线面垂直. 【做一做1】 垂直于梯形两腰的直线与梯形所在平面的位置关系是( )
A.垂直 B.斜交
C.平行 D.不能确定
解析:梯形的两腰所在的直线相交,根据线面垂直的判定定理可知选项A正确.
答案:A名师点拨理解线面垂直的判定定理注意以下几点:
(1)定理可表述为“线线垂直,则线面垂直”.
(2)“两条相交直线”是关键词,一定不要忽视这个条件,否则将导致结论错误,即“线不在多,相交就行”.
(3)要证明一条直线与一个平面垂直,只需在平面内找到两条相交直线和该直线垂直即可,至于这两条相交直线是否和已知直线有公共点无关紧要.
(4)线面垂直的判定定理与线面垂直的定义往往在证题过程中要反复交替使用.2.二面角及其平面角
(1)半平面的定义:一个平面内的一条直线,把这个平面分成两部分,其中的每一部分都叫作半平面.
(2)二面角的定义:从一条直线出发的两个半平面所组成的图形叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.
(3)二面角的记法:
以直线AB为棱,半平面α,β为面的二面角,记作二面角α-AB-β.
(4)二面角的平面角:
以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角.
(5)直二面角:平面角是直角的二面角叫作直二面角.【做一做2】 给出下列命题:
①两个相交平面组成的图形叫作二面角;
②异面直线a,b分别和一个二面角的两个面垂直,则a,b所成的角与这个二面角的平面角相等或互补;
③二面角的平面角是从棱上一点出发,分别在两个面内作射线所成的角;
④二面角的大小与其平面角的顶点在棱上的位置没有关系.
其中正确的是( )
A.①③ B.②④ C.③④ D.①②
解析:由二面角的定义:从一条直线出发的两个半平面所组成的图形叫作二面角,可知①不对.画出图形,可知②正确.③中所作的射线不一定垂直于二面角的棱,故③不对.由定义知④正确.故选B.
答案:B3.平面与平面垂直
(1)两个平面互相垂直的定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.
(2)画法:在画两个垂直的平面时,通常把表示直立平面的平行四边形的竖边画成和表示水平平面的平行四边形的横边垂直.如图①②所示.(3)平面与平面垂直的判定定理
①文字叙述:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
②符号表示:③图形表示: ④作用:线面垂直?面面垂直. 【做一做3】 已知直线m,n与平面α,β,γ,下列可能使α⊥β成立的条件是( )
A.α⊥γ,β⊥γ B.α∩β=m,m⊥n,n?β
C.m∥α,m∥β D.m∥α,m⊥β
解析:选择适合条件的几何图形观察可得,A中α∥β或α与β相交,B中α,β相交,但不一定垂直,C中α∥β或α与β相交.
答案:D名师点拨理解面面垂直的判定定理注意以下几点:
(1)定理可简记为“线面垂直,则面面垂直”,因此要证明平面与平面垂直,只需在其中一个平面内找另一个平面的垂线,即证“线面垂直”.
(2)两个平面垂直的判定定理,不仅仅是判定两个平面垂直的依据,而且是找出垂直于一个平面的另一个平面的依据.
(3)要证α⊥β,可证α经过β的某一条垂线,也可证明β经过α的某一条垂线.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若直线l垂直于平面α内无数条直线,则有l⊥α. ( )
(2)若直线l垂直于平面α内任意直线,则有l⊥α. ( )
(3)若直线l垂直于α内的一个凸五边形的两条边,则有l⊥α. ( )
(4)一个二面角的平面角有且只有一个. ( )
(5)若直线l与平面α交于点O,且l与α不垂直,l?β,则α与β一定不垂直. ( )× √ √ × × 探究一探究二易错辨析探究一线面垂直及其判定
【例1】 如图所示,在三棱锥A-BCD中,BC=AC,AD=BD,作BE⊥CD,E为垂足,作AH⊥BE于点H.求证:AH⊥平面BCD.探究一探究二易错辨析证明:取AB的中点F,连接CF,DF,因为AC=BC,所以CF⊥AB.
同理可得,DF⊥AB.
又CF∩DF=F,
所以AB⊥平面CDF.
因为CD?平面CDF,
所以AB⊥CD.
又BE⊥CD,且BE∩AB=B,所以CD⊥平面ABE.
因为AH?平面ABE,所以CD⊥AH.
又AH⊥BE,BE∩CD=E,所以AH⊥平面BCD.探究一探究二易错辨析反思感悟证明线面垂直的关键是分析几何图形,寻找隐含的和题目中推导出的线线垂直关系,进而证明线面垂直.三角形全等、等腰三角形底边上的中线、梯形的高、菱形和正方形的对角线、三角形中的勾股定理等都是找线线垂直的方法.变式训练1如图所示,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆O上的点.求证:BC⊥平面PAC.?
分析:由AB是圆O的直径可知AC⊥BC,再结合PA⊥平面ABC,即可证明BC⊥平面PAC.探究一探究二易错辨析证明:由AB是圆O的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.探究一探究二易错辨析探究二面面垂直的判定?
【例2】 如图所示,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2 ,E,F分别是AB,PD的中点.求证:(1)AF∥平面PCE;
(2)平面PCE⊥平面PCD.探究一探究二易错辨析分析:(1)要证AF∥平面PCE,只需证明AF平行于平面PCE内的一条直线即可,取PC的中点G,则该直线为GE.
(2)要证明平面PCE⊥平面PCD,只需证明GE⊥平面PCD,而由(1)知GE∥AF,故只需证明AF⊥平面PCD即可.探究一探究二易错辨析证明:(1)取PC的中点G,连接FG,EG, ∵F为PD的中点,E为AB的中点,
∴FG= CD,且FG∥CD,AE= CD,且AE∥CD,
∴FG=AE,且FG∥AE,
∴四边形AEGF为平行四边形,∴AF∥GE.
∵GE?平面PEC,AF?平面PCE,∴AF∥平面PCE.
(2)∵PA=AD=2,∴AF⊥PD.
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
∵AD⊥CD,PA∩AD=A,
∴CD⊥平面PAD.∵AF?平面PAD,∴AF⊥CD.
∵PD∩CD=D,∴AF⊥平面PCD,
∴GE⊥平面PCD.
∵GE?平面PEC,∴平面PCE⊥平面PCD.探究一探究二易错辨析反思感悟怎样证明平面与平面垂直
1.证明面面垂直的方法:(1)证明两个半平面构成的二面角的平面角为90°;(2)证明一个平面经过另一个平面的一条垂线,将证明面面垂直的问题转化为证明线面垂直的问题.
2.利用判定定理证明两个平面垂直时,一般方法是先从现有的直线中寻找平面的垂线,若图形中不存在这样的垂线,则可通过作辅助线来解决,而作辅助线则应有理论根据并且要有利于证明.探究一探究二易错辨析变式训练2已知正方形ABCD的边长为1,分别取边BC,CD的中点E,F,连接AE,EF,AF,以AE,EF,FA为折痕,折叠使点B,C,D重合于一点P.求证:
(1)AP⊥EF;
(2)平面APE⊥平面APF.探究一探究二易错辨析证明:(1)∵∠APE=∠APF=90°,
∴AP⊥PE,AP⊥PF.
∵PE∩PF=P,∴PA⊥平面PEF.
∵EF?平面PEF,∴PA⊥EF.
(2)∵∠APE=∠EPF=90°,
∴PE⊥AP,PE⊥PF.
∵AP∩PF=P,∴PE⊥平面APF.
∵PE?平面APE,
∴平面APE⊥平面APF.探究一探究二易错辨析对空间中线面关系理解不透彻而致误
【典例】 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,则截面ACB1与对角面BB1D1D垂直吗?
错解如图所示,设AC与BD的交点为O,连接B1O,
则B1O是截面ACB1与对角面BB1D1D的交线.
∵B1O不与底面垂直,
∴截面ACB1不可能与对角面BB1D1D垂直.探究一探究二易错辨析纠错心得1.因为B1O与底面不垂直,就断定截面ACB1不可能与对角面BB1D1D垂直,这是毫无根据的.
2.要克服上述错误,一定要将有关定理或性质的适用条件及内涵把握清楚,不能凭想当然进行毫无逻辑的论证.正解:∵四边形ABCD是正方形,∴AC⊥BD.
∵BB1⊥底面ABCD,∴AC⊥B1B.
∵B1B∩BD=B,∴AC⊥对角面BB1D1D.
∵AC?截面ACB1,∴截面ACB1⊥对角面BB1D1D.123451.下列各种情况中,一条直线垂直于一个平面内的:①三角形的两条边;②梯形的两条边;③圆的两条直径;④正六边形的两条边.不能保证该直线与平面垂直的是( )
A.①③ B.②
C.②④ D.①②④
解析:三角形的任何两边都相交;圆的任何两条直径都相交;但梯形中任意两边不一定相交,也可能平行;正六边形中也存在平行的两条边,因此不能保证该直线与平面垂直的是②④.故选C.
答案:C123452.在空间四边形ABCD中,若AD⊥BC,BD⊥AD,则( )
A.平面ABC⊥平面ADC B.平面ABC⊥平面ADB
C.平面ABC⊥平面DBC D.平面ADC⊥平面DBC
解析:如图所示,∵AD⊥BC,AD⊥BD,BC∩BD=B,
∴AD⊥平面BDC.
又AD?平面ADC,
∴平面ADC⊥平面DBC.
答案:D123453.如图所示,∠BCA=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,
(1)与PC垂直的直线有 ?;?
(2)与AP垂直的直线有 ?.?
解析:(1)因为PC⊥平面ABC,AB,AC,BC?平面ABC,
所以与PC垂直的直线有AB,AC,BC.
(2)∠BCA=90°,即BC⊥AC.
又BC⊥PC,AC∩PC=C,
所以BC⊥平面PAC,PA?平面PAC.所以BC⊥AP.
答案:(1)AB,AC,BC (2)BC123454.如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列说法正确的个数为( )
①C1M∥AC;
②BD1⊥AC;
③BC1与AC所成的角为60°;
④CD与BN为异面直线.
A.1 B.2 C.3 D.412345解析:由正方体ABCD-A1B1C1D1中,M,N分别为A1D1和AA1的中点,可知:在①中,AC∥A1C1,A1C1∩C1M=C1,∴C1M与AC是异面直线,故①错误;
在②中,∵AC⊥DD1,AC⊥BD,BD∩DD1=D,
∴AC⊥平面BDD1.
又BD1?平面BDD1,
∴BD1⊥AC,故②正确;
在③中,AC∥A1C1,BC1=A1C1=BA1,
∴BC1与AC所成的角为60°,故③正确;
在④中,CD∥AB,AB∩BN=B,故CD与BN为异面直线,故④正确.故选C.
答案:C123455.如图所示,四边形ABCD是菱形,PC⊥平面ABCD,E是PA的中点,求证:平面BDE⊥平面ABCD.
证明:连接AC交BD于点O,连接OE.
因为O为AC的中点,E为PA的中点,
所以EO是△PAC的中位线,EO∥PC.
因为PC⊥平面ABCD,
所以EO⊥平面ABCD.
又EO ?平面BDE,所以平面BDE⊥平面ABCD.
(1)直线与平面垂直的定义
如果一条直线和一个平面内的任何一条直线都垂直,那么称这条直线和这个平面垂直.
(2)画法:当直线与平面垂直时,通常把表示直线的线段画成和表示平面的平行四边形的横边垂直.如图所示.(3)直线与平面垂直的判定定理
①文字叙述:如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
②符号表示:若直线a?α,直线b?α,直线l⊥a,l⊥b,a∩b=A,则l⊥α.③图形表示: ④作用:线线垂直?线面垂直. 【做一做1】 垂直于梯形两腰的直线与梯形所在平面的位置关系是( )
A.垂直 B.斜交
C.平行 D.不能确定
解析:梯形的两腰所在的直线相交,根据线面垂直的判定定理可知选项A正确.
答案:A名师点拨理解线面垂直的判定定理注意以下几点:
(1)定理可表述为“线线垂直,则线面垂直”.
(2)“两条相交直线”是关键词,一定不要忽视这个条件,否则将导致结论错误,即“线不在多,相交就行”.
(3)要证明一条直线与一个平面垂直,只需在平面内找到两条相交直线和该直线垂直即可,至于这两条相交直线是否和已知直线有公共点无关紧要.
(4)线面垂直的判定定理与线面垂直的定义往往在证题过程中要反复交替使用.2.二面角及其平面角
(1)半平面的定义:一个平面内的一条直线,把这个平面分成两部分,其中的每一部分都叫作半平面.
(2)二面角的定义:从一条直线出发的两个半平面所组成的图形叫作二面角,这条直线叫作二面角的棱,这两个半平面叫作二面角的面.
(3)二面角的记法:
以直线AB为棱,半平面α,β为面的二面角,记作二面角α-AB-β.
(4)二面角的平面角:
以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角.
(5)直二面角:平面角是直角的二面角叫作直二面角.【做一做2】 给出下列命题:
①两个相交平面组成的图形叫作二面角;
②异面直线a,b分别和一个二面角的两个面垂直,则a,b所成的角与这个二面角的平面角相等或互补;
③二面角的平面角是从棱上一点出发,分别在两个面内作射线所成的角;
④二面角的大小与其平面角的顶点在棱上的位置没有关系.
其中正确的是( )
A.①③ B.②④ C.③④ D.①②
解析:由二面角的定义:从一条直线出发的两个半平面所组成的图形叫作二面角,可知①不对.画出图形,可知②正确.③中所作的射线不一定垂直于二面角的棱,故③不对.由定义知④正确.故选B.
答案:B3.平面与平面垂直
(1)两个平面互相垂直的定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.
(2)画法:在画两个垂直的平面时,通常把表示直立平面的平行四边形的竖边画成和表示水平平面的平行四边形的横边垂直.如图①②所示.(3)平面与平面垂直的判定定理
①文字叙述:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
②符号表示:③图形表示: ④作用:线面垂直?面面垂直. 【做一做3】 已知直线m,n与平面α,β,γ,下列可能使α⊥β成立的条件是( )
A.α⊥γ,β⊥γ B.α∩β=m,m⊥n,n?β
C.m∥α,m∥β D.m∥α,m⊥β
解析:选择适合条件的几何图形观察可得,A中α∥β或α与β相交,B中α,β相交,但不一定垂直,C中α∥β或α与β相交.
答案:D名师点拨理解面面垂直的判定定理注意以下几点:
(1)定理可简记为“线面垂直,则面面垂直”,因此要证明平面与平面垂直,只需在其中一个平面内找另一个平面的垂线,即证“线面垂直”.
(2)两个平面垂直的判定定理,不仅仅是判定两个平面垂直的依据,而且是找出垂直于一个平面的另一个平面的依据.
(3)要证α⊥β,可证α经过β的某一条垂线,也可证明β经过α的某一条垂线.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)若直线l垂直于平面α内无数条直线,则有l⊥α. ( )
(2)若直线l垂直于平面α内任意直线,则有l⊥α. ( )
(3)若直线l垂直于α内的一个凸五边形的两条边,则有l⊥α. ( )
(4)一个二面角的平面角有且只有一个. ( )
(5)若直线l与平面α交于点O,且l与α不垂直,l?β,则α与β一定不垂直. ( )× √ √ × × 探究一探究二易错辨析探究一线面垂直及其判定
【例1】 如图所示,在三棱锥A-BCD中,BC=AC,AD=BD,作BE⊥CD,E为垂足,作AH⊥BE于点H.求证:AH⊥平面BCD.探究一探究二易错辨析证明:取AB的中点F,连接CF,DF,因为AC=BC,所以CF⊥AB.
同理可得,DF⊥AB.
又CF∩DF=F,
所以AB⊥平面CDF.
因为CD?平面CDF,
所以AB⊥CD.
又BE⊥CD,且BE∩AB=B,所以CD⊥平面ABE.
因为AH?平面ABE,所以CD⊥AH.
又AH⊥BE,BE∩CD=E,所以AH⊥平面BCD.探究一探究二易错辨析反思感悟证明线面垂直的关键是分析几何图形,寻找隐含的和题目中推导出的线线垂直关系,进而证明线面垂直.三角形全等、等腰三角形底边上的中线、梯形的高、菱形和正方形的对角线、三角形中的勾股定理等都是找线线垂直的方法.变式训练1如图所示,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆O上的点.求证:BC⊥平面PAC.?
分析:由AB是圆O的直径可知AC⊥BC,再结合PA⊥平面ABC,即可证明BC⊥平面PAC.探究一探究二易错辨析证明:由AB是圆O的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.探究一探究二易错辨析探究二面面垂直的判定?
【例2】 如图所示,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2 ,E,F分别是AB,PD的中点.求证:(1)AF∥平面PCE;
(2)平面PCE⊥平面PCD.探究一探究二易错辨析分析:(1)要证AF∥平面PCE,只需证明AF平行于平面PCE内的一条直线即可,取PC的中点G,则该直线为GE.
(2)要证明平面PCE⊥平面PCD,只需证明GE⊥平面PCD,而由(1)知GE∥AF,故只需证明AF⊥平面PCD即可.探究一探究二易错辨析证明:(1)取PC的中点G,连接FG,EG, ∵F为PD的中点,E为AB的中点,
∴FG= CD,且FG∥CD,AE= CD,且AE∥CD,
∴FG=AE,且FG∥AE,
∴四边形AEGF为平行四边形,∴AF∥GE.
∵GE?平面PEC,AF?平面PCE,∴AF∥平面PCE.
(2)∵PA=AD=2,∴AF⊥PD.
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD.
∵AD⊥CD,PA∩AD=A,
∴CD⊥平面PAD.∵AF?平面PAD,∴AF⊥CD.
∵PD∩CD=D,∴AF⊥平面PCD,
∴GE⊥平面PCD.
∵GE?平面PEC,∴平面PCE⊥平面PCD.探究一探究二易错辨析反思感悟怎样证明平面与平面垂直
1.证明面面垂直的方法:(1)证明两个半平面构成的二面角的平面角为90°;(2)证明一个平面经过另一个平面的一条垂线,将证明面面垂直的问题转化为证明线面垂直的问题.
2.利用判定定理证明两个平面垂直时,一般方法是先从现有的直线中寻找平面的垂线,若图形中不存在这样的垂线,则可通过作辅助线来解决,而作辅助线则应有理论根据并且要有利于证明.探究一探究二易错辨析变式训练2已知正方形ABCD的边长为1,分别取边BC,CD的中点E,F,连接AE,EF,AF,以AE,EF,FA为折痕,折叠使点B,C,D重合于一点P.求证:
(1)AP⊥EF;
(2)平面APE⊥平面APF.探究一探究二易错辨析证明:(1)∵∠APE=∠APF=90°,
∴AP⊥PE,AP⊥PF.
∵PE∩PF=P,∴PA⊥平面PEF.
∵EF?平面PEF,∴PA⊥EF.
(2)∵∠APE=∠EPF=90°,
∴PE⊥AP,PE⊥PF.
∵AP∩PF=P,∴PE⊥平面APF.
∵PE?平面APE,
∴平面APE⊥平面APF.探究一探究二易错辨析对空间中线面关系理解不透彻而致误
【典例】 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,则截面ACB1与对角面BB1D1D垂直吗?
错解如图所示,设AC与BD的交点为O,连接B1O,
则B1O是截面ACB1与对角面BB1D1D的交线.
∵B1O不与底面垂直,
∴截面ACB1不可能与对角面BB1D1D垂直.探究一探究二易错辨析纠错心得1.因为B1O与底面不垂直,就断定截面ACB1不可能与对角面BB1D1D垂直,这是毫无根据的.
2.要克服上述错误,一定要将有关定理或性质的适用条件及内涵把握清楚,不能凭想当然进行毫无逻辑的论证.正解:∵四边形ABCD是正方形,∴AC⊥BD.
∵BB1⊥底面ABCD,∴AC⊥B1B.
∵B1B∩BD=B,∴AC⊥对角面BB1D1D.
∵AC?截面ACB1,∴截面ACB1⊥对角面BB1D1D.123451.下列各种情况中,一条直线垂直于一个平面内的:①三角形的两条边;②梯形的两条边;③圆的两条直径;④正六边形的两条边.不能保证该直线与平面垂直的是( )
A.①③ B.②
C.②④ D.①②④
解析:三角形的任何两边都相交;圆的任何两条直径都相交;但梯形中任意两边不一定相交,也可能平行;正六边形中也存在平行的两条边,因此不能保证该直线与平面垂直的是②④.故选C.
答案:C123452.在空间四边形ABCD中,若AD⊥BC,BD⊥AD,则( )
A.平面ABC⊥平面ADC B.平面ABC⊥平面ADB
C.平面ABC⊥平面DBC D.平面ADC⊥平面DBC
解析:如图所示,∵AD⊥BC,AD⊥BD,BC∩BD=B,
∴AD⊥平面BDC.
又AD?平面ADC,
∴平面ADC⊥平面DBC.
答案:D123453.如图所示,∠BCA=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,
(1)与PC垂直的直线有 ?;?
(2)与AP垂直的直线有 ?.?
解析:(1)因为PC⊥平面ABC,AB,AC,BC?平面ABC,
所以与PC垂直的直线有AB,AC,BC.
(2)∠BCA=90°,即BC⊥AC.
又BC⊥PC,AC∩PC=C,
所以BC⊥平面PAC,PA?平面PAC.所以BC⊥AP.
答案:(1)AB,AC,BC (2)BC123454.如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列说法正确的个数为( )
①C1M∥AC;
②BD1⊥AC;
③BC1与AC所成的角为60°;
④CD与BN为异面直线.
A.1 B.2 C.3 D.412345解析:由正方体ABCD-A1B1C1D1中,M,N分别为A1D1和AA1的中点,可知:在①中,AC∥A1C1,A1C1∩C1M=C1,∴C1M与AC是异面直线,故①错误;
在②中,∵AC⊥DD1,AC⊥BD,BD∩DD1=D,
∴AC⊥平面BDD1.
又BD1?平面BDD1,
∴BD1⊥AC,故②正确;
在③中,AC∥A1C1,BC1=A1C1=BA1,
∴BC1与AC所成的角为60°,故③正确;
在④中,CD∥AB,AB∩BN=B,故CD与BN为异面直线,故④正确.故选C.
答案:C123455.如图所示,四边形ABCD是菱形,PC⊥平面ABCD,E是PA的中点,求证:平面BDE⊥平面ABCD.
证明:连接AC交BD于点O,连接OE.
因为O为AC的中点,E为PA的中点,
所以EO是△PAC的中位线,EO∥PC.
因为PC⊥平面ABCD,
所以EO⊥平面ABCD.
又EO ?平面BDE,所以平面BDE⊥平面ABCD.
