五年级上册数学一课一练-6.4组合图形的面积 人教新课标(2014秋)(含答案)
文档属性
| 名称 | 五年级上册数学一课一练-6.4组合图形的面积 人教新课标(2014秋)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-08 00:00:00 | ||
图片预览

文档简介
五年级上册数学一课一练-6.4组合图形的面积
一、单选题
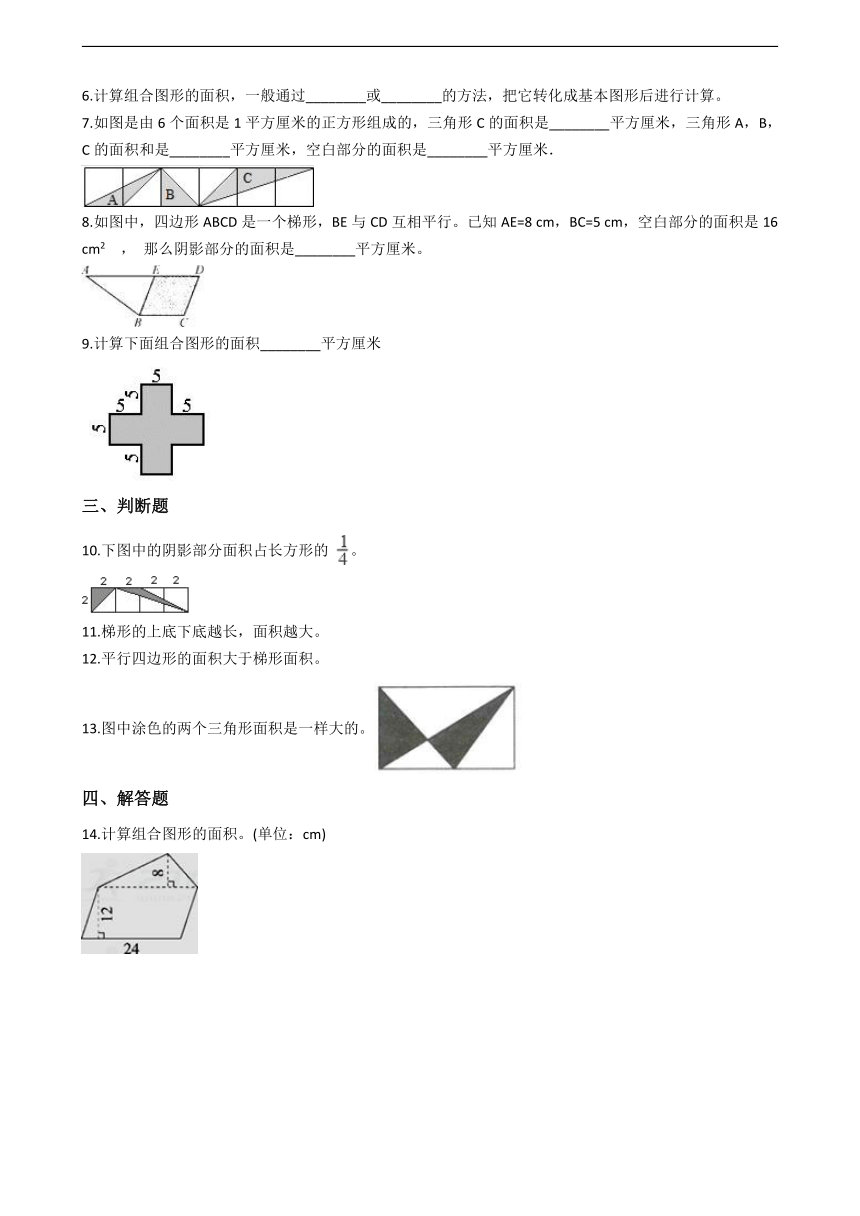
1.如图两个图中阴影部分的( )
A.?周长相等,面积不相等????????????B.?周长和面积都相等????????????C.?周长不相等,面积相等?????????
2.下面三幅图的阴影部分的面积相比较,(??? )的面积大。
A.?图(1)大???????????????????????????????B.?图(2)大???????????????????????????????C.?图(3)大???????????????????????????????D.?同样大
3.在如图梯形中,两个阴影部分的面积相比(?? )
A.?甲大于乙???????????????????????????B.?乙大于甲???????????????????????????C.?甲等于乙???????????????????????????D.?无法比较
4.如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是(???? )平方厘米。
A.?24?????????????????????????????????????????B.?36?????????????????????????????????????????C.?48?????????????????????????????????????????D.?72
二、填空题
5.求下面图中阴影部分的面积. 面积是________
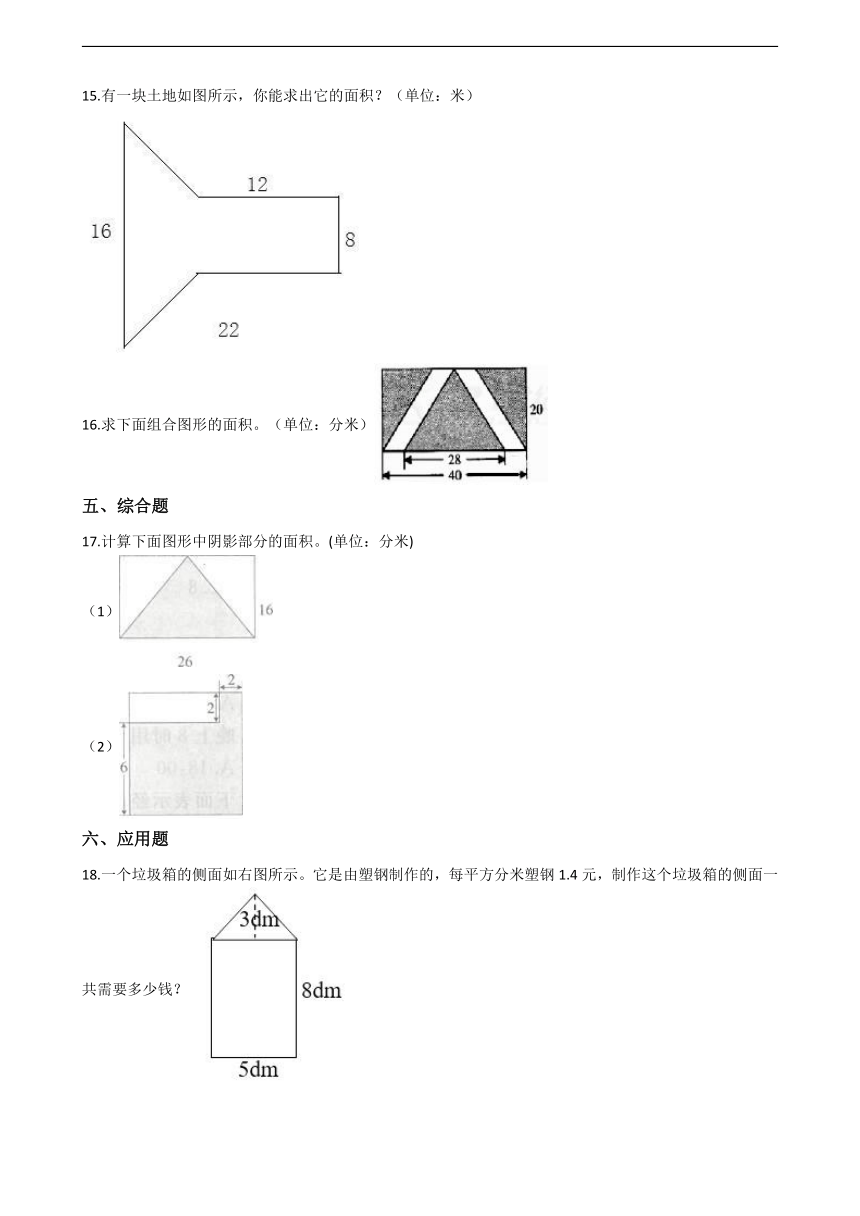
6.计算组合图形的面积,一般通过________或________的方法,把它转化成基本图形后进行计算。
7.如图是由6个面积是1平方厘米的正方形组成的,三角形C的面积是________平方厘米,三角形A,B,C的面积和是________平方厘米,空白部分的面积是________平方厘米.
8.如图中,四边形ABCD是一个梯形,BE与CD互相平行。已知AE=8 cm,BC=5 cm,空白部分的面积是16 cm2 , 那么阴影部分的面积是________平方厘米。
9.计算下面组合图形的面积________平方厘米
三、判断题
10.下图中的阴影部分面积占长方形的 。
11.梯形的上底下底越长,面积越大。
12.平行四边形的面积大于梯形面积。
13.图中涂色的两个三角形面积是一样大的。
四、解答题
14.计算组合图形的面积。(单位:cm)
15.有一块土地如图所示,你能求出它的面积?(单位:米)
16.求下面组合图形的面积。(单位:分米)
五、综合题
17.计算下面图形中阴影部分的面积。(单位:分米)
(1)
(2)
六、应用题
18.一个垃圾箱的侧面如右图所示。它是由塑钢制作的,每平方分米塑钢1.4元,制作这个垃圾箱的侧面一共需要多少钱?
19.在长方形ABCD中,AB=8,BC=15,E是CD的中点,F是BC的中点,连接BD,AE,AF把图形分成六块,求阴影部分的面积和是多少?
参考答案
一、单选题
1.【答案】C
2.【答案】 D
3.【答案】C
4.【答案】C
二、填空题
5.【答案】3.72
6.【答案】分割法;添补
7.【答案】1;2;4
8.【答案】20
9.【答案】 125
三、判断题
10.【答案】
11.【答案】错误
12.【答案】错误
13.【答案】正确
四、解答题
14.【答案】24×8÷2+24×12=384(cm2) 答:组合图形的面积为384cm2。
15.【答案】解:
8×22+(22-12)×(16-8)=256(平方米)
16.【答案】解:40×20-(40-28)×20 =800-240 =560(平方分米)
五、综合题
17.【答案】(1)解:26×16÷2 =416÷2 =208(平方分米) (2)解:6×6=36(平方分米),2×2=4(平方分米),36+4=40(平方分米)
六、应用题
18.【答案】解:5×3÷2+5×8 =15÷2+40 =7.5+40 =47.5(平方分米)47.5×1.4=66.5(元) 答:制作这个垃圾箱的侧面一共需要66.5元.
19.【答案】解:假设BD交AF与G点,AE交DB与H点,因为BF与AD平行,并且等于AD的 , 所以BG:GD=BF:AD=1:2,则BG:BD=1:3, 同样的方法可以得出:DH:BD=1:3, 所以BG=DH= BD,所以BG=GH=HD, 所以△ABG与△AGH的面积相等, △ABG的面积+△BGF的面积=△AGH的面积+△BGF的面积, △AGH的面积+△BGF的面积=△ABF的面积= ×8× =30(平方厘米); 又因为△DEH的DE边上的高= ×15=5(厘米), 所以△DEH面积= × ×5=10(平方厘米); 即阴影部分面积=30+10=40(平方厘米). 答:阴影部分的面积和是40平方厘米.
一、单选题
1.如图两个图中阴影部分的( )
A.?周长相等,面积不相等????????????B.?周长和面积都相等????????????C.?周长不相等,面积相等?????????
2.下面三幅图的阴影部分的面积相比较,(??? )的面积大。
A.?图(1)大???????????????????????????????B.?图(2)大???????????????????????????????C.?图(3)大???????????????????????????????D.?同样大
3.在如图梯形中,两个阴影部分的面积相比(?? )
A.?甲大于乙???????????????????????????B.?乙大于甲???????????????????????????C.?甲等于乙???????????????????????????D.?无法比较
4.如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是(???? )平方厘米。
A.?24?????????????????????????????????????????B.?36?????????????????????????????????????????C.?48?????????????????????????????????????????D.?72
二、填空题
5.求下面图中阴影部分的面积. 面积是________
6.计算组合图形的面积,一般通过________或________的方法,把它转化成基本图形后进行计算。
7.如图是由6个面积是1平方厘米的正方形组成的,三角形C的面积是________平方厘米,三角形A,B,C的面积和是________平方厘米,空白部分的面积是________平方厘米.
8.如图中,四边形ABCD是一个梯形,BE与CD互相平行。已知AE=8 cm,BC=5 cm,空白部分的面积是16 cm2 , 那么阴影部分的面积是________平方厘米。
9.计算下面组合图形的面积________平方厘米
三、判断题
10.下图中的阴影部分面积占长方形的 。
11.梯形的上底下底越长,面积越大。
12.平行四边形的面积大于梯形面积。
13.图中涂色的两个三角形面积是一样大的。
四、解答题
14.计算组合图形的面积。(单位:cm)
15.有一块土地如图所示,你能求出它的面积?(单位:米)
16.求下面组合图形的面积。(单位:分米)
五、综合题
17.计算下面图形中阴影部分的面积。(单位:分米)
(1)
(2)
六、应用题
18.一个垃圾箱的侧面如右图所示。它是由塑钢制作的,每平方分米塑钢1.4元,制作这个垃圾箱的侧面一共需要多少钱?
19.在长方形ABCD中,AB=8,BC=15,E是CD的中点,F是BC的中点,连接BD,AE,AF把图形分成六块,求阴影部分的面积和是多少?
参考答案
一、单选题
1.【答案】C
2.【答案】 D
3.【答案】C
4.【答案】C
二、填空题
5.【答案】3.72
6.【答案】分割法;添补
7.【答案】1;2;4
8.【答案】20
9.【答案】 125
三、判断题
10.【答案】
11.【答案】错误
12.【答案】错误
13.【答案】正确
四、解答题
14.【答案】24×8÷2+24×12=384(cm2) 答:组合图形的面积为384cm2。
15.【答案】解:
8×22+(22-12)×(16-8)=256(平方米)
16.【答案】解:40×20-(40-28)×20 =800-240 =560(平方分米)
五、综合题
17.【答案】(1)解:26×16÷2 =416÷2 =208(平方分米) (2)解:6×6=36(平方分米),2×2=4(平方分米),36+4=40(平方分米)
六、应用题
18.【答案】解:5×3÷2+5×8 =15÷2+40 =7.5+40 =47.5(平方分米)47.5×1.4=66.5(元) 答:制作这个垃圾箱的侧面一共需要66.5元.
19.【答案】解:假设BD交AF与G点,AE交DB与H点,因为BF与AD平行,并且等于AD的 , 所以BG:GD=BF:AD=1:2,则BG:BD=1:3, 同样的方法可以得出:DH:BD=1:3, 所以BG=DH= BD,所以BG=GH=HD, 所以△ABG与△AGH的面积相等, △ABG的面积+△BGF的面积=△AGH的面积+△BGF的面积, △AGH的面积+△BGF的面积=△ABF的面积= ×8× =30(平方厘米); 又因为△DEH的DE边上的高= ×15=5(厘米), 所以△DEH面积= × ×5=10(平方厘米); 即阴影部分面积=30+10=40(平方厘米). 答:阴影部分的面积和是40平方厘米.
