2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的简单几何性质(30张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的简单几何性质(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 00:00:00 | ||
图片预览










文档简介
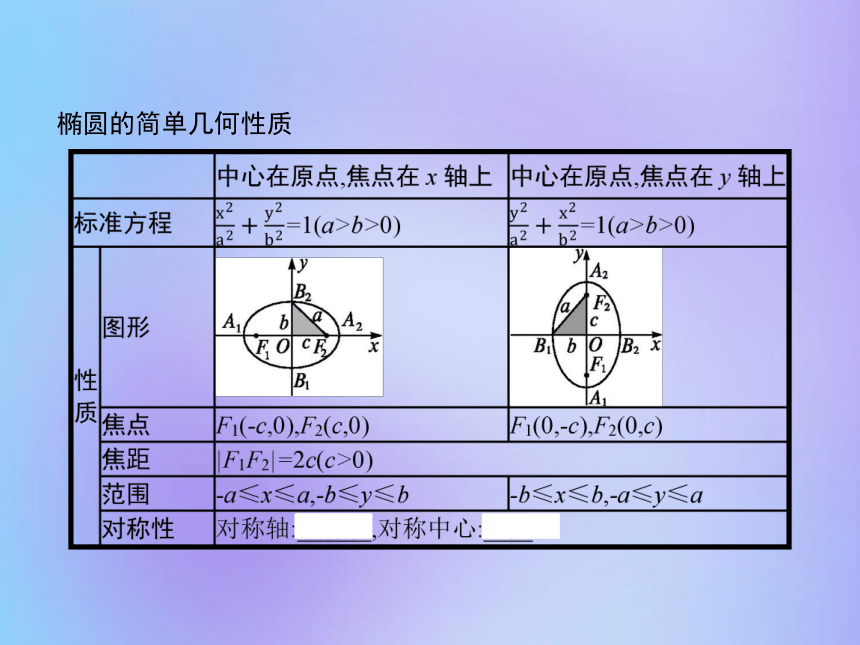
课件30张PPT。2.1.2 椭圆的简单几何性质椭圆的简单几何性质 名师点拨1.椭圆的范围决定了椭圆的大小,它位于直线x=±a和y=±b所围成的矩形框里.其实质是给出了椭圆上点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值和轨迹等问题时的检验.
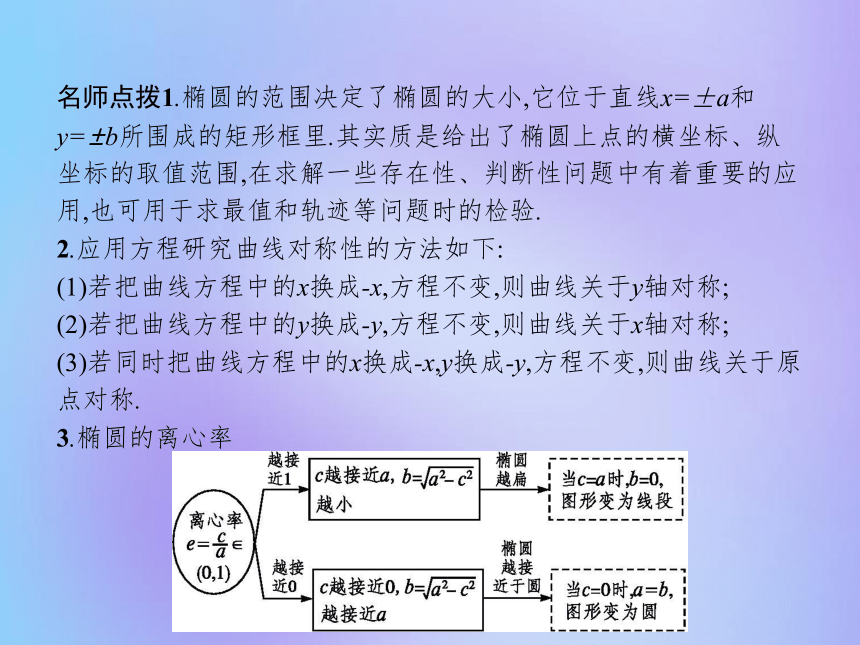
2.应用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
3.椭圆的离心率【做一做1】 椭圆x2+9y2=36的短轴端点为 .?
解析:椭圆方程化为 ,焦点在x轴上,b=2,所以短轴端点为(0,±2).
答案:(0,±2)思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)椭圆的顶点坐标、长轴长、短轴长、离心率等都与椭圆焦点所在的坐标轴有关. ( )
(2)椭圆的焦点一定在长轴上. ( )答案:(1)× (2)√ (3)× (4)× (5)√ 探究一探究二探究三思维辨析根据椭圆的标准方程研究其几何性质
【例1】 已知椭圆mx2+4y2=4m(m>0)的离心率为 ,求椭圆的长轴长、短轴长、焦点坐标及顶点坐标.
思路点拨:先根据离心率的值求出m的值,再得到其他几何性质,但要注意对m进行分类讨论,以确定焦点的位置.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟根据椭圆方程确定其几何性质的步骤如下:
(1)化标准:把椭圆方程化成标准形式;
(2)定位置:根据标准方程分母的大小确定焦点的位置;
(3)求参数:写出a,b的值,并求出c的值;
(4)写性质:按要求写出椭圆的简单几何性质.探究一探究二探究三思维辨析探究一探究二探究三思维辨析根据椭圆的几何性质求其标准方程
【例2】 根据下列条件求椭圆的标准方程:
(1)椭圆的一个顶点是(0,2),离心率e= ;
(2)椭圆长轴的一个端点为(-6,0),短轴的一个端点与两个焦点构成一个正三角形.
思路点拨:(1)焦点位置不确定,应进行分类讨论;(2)焦点位置确定,可根据题目条件求出a,b,c的值即得方程.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟1.根据椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆标准方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行分类讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.探究一探究二探究三思维辨析变式训练2根据下列条件,求椭圆的标准方程.
(1)已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0).
(2)在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为8.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析椭圆的离心率问题
【例3】(1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围;
(2)椭圆 (a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为c,求椭圆的离心率.
思路点拨:(1)依题意建立c与b的不等式,再转化为a,c的不等式,即可求得离心率的取值范围;(2)根据题意,建立参数a,b,c的方程求解,注意椭圆定义的灵活运用.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视对椭圆焦点位置的讨论致误
【典例】 已知椭圆x2+my2=1的离心率为 ,求它的长轴长.
易错分析:本题常见错误:一是没有将所给椭圆方程化为标准形式而求解;二是将椭圆方程化为标准形式后,不讨论焦点所在的坐标轴,只就其中的一种情况求解.探究一探究二探究三思维辨析纠错心得:已知椭圆离心率的值时,椭圆的焦点位置是不确定的,焦点可以在x轴上,也可以在y轴上,因此在求解时应分类讨论,避免漏解.探究一探究二探究三思维辨析
2.应用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
3.椭圆的离心率【做一做1】 椭圆x2+9y2=36的短轴端点为 .?
解析:椭圆方程化为 ,焦点在x轴上,b=2,所以短轴端点为(0,±2).
答案:(0,±2)思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)椭圆的顶点坐标、长轴长、短轴长、离心率等都与椭圆焦点所在的坐标轴有关. ( )
(2)椭圆的焦点一定在长轴上. ( )答案:(1)× (2)√ (3)× (4)× (5)√ 探究一探究二探究三思维辨析根据椭圆的标准方程研究其几何性质
【例1】 已知椭圆mx2+4y2=4m(m>0)的离心率为 ,求椭圆的长轴长、短轴长、焦点坐标及顶点坐标.
思路点拨:先根据离心率的值求出m的值,再得到其他几何性质,但要注意对m进行分类讨论,以确定焦点的位置.探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟根据椭圆方程确定其几何性质的步骤如下:
(1)化标准:把椭圆方程化成标准形式;
(2)定位置:根据标准方程分母的大小确定焦点的位置;
(3)求参数:写出a,b的值,并求出c的值;
(4)写性质:按要求写出椭圆的简单几何性质.探究一探究二探究三思维辨析探究一探究二探究三思维辨析根据椭圆的几何性质求其标准方程
【例2】 根据下列条件求椭圆的标准方程:
(1)椭圆的一个顶点是(0,2),离心率e= ;
(2)椭圆长轴的一个端点为(-6,0),短轴的一个端点与两个焦点构成一个正三角形.
思路点拨:(1)焦点位置不确定,应进行分类讨论;(2)焦点位置确定,可根据题目条件求出a,b,c的值即得方程.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析反思感悟1.根据椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆标准方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行分类讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.探究一探究二探究三思维辨析变式训练2根据下列条件,求椭圆的标准方程.
(1)已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0).
(2)在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为8.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析椭圆的离心率问题
【例3】(1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围;
(2)椭圆 (a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为c,求椭圆的离心率.
思路点拨:(1)依题意建立c与b的不等式,再转化为a,c的不等式,即可求得离心率的取值范围;(2)根据题意,建立参数a,b,c的方程求解,注意椭圆定义的灵活运用.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视对椭圆焦点位置的讨论致误
【典例】 已知椭圆x2+my2=1的离心率为 ,求它的长轴长.
易错分析:本题常见错误:一是没有将所给椭圆方程化为标准形式而求解;二是将椭圆方程化为标准形式后,不讨论焦点所在的坐标轴,只就其中的一种情况求解.探究一探究二探究三思维辨析纠错心得:已知椭圆离心率的值时,椭圆的焦点位置是不确定的,焦点可以在x轴上,也可以在y轴上,因此在求解时应分类讨论,避免漏解.探究一探究二探究三思维辨析
