2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程(27张PPT)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 775.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-09 00:00:00 | ||
图片预览








文档简介
课件27张PPT。2.2.1 双曲线及其标准方程1.双曲线的定义 名师点拨理解双曲线的定义,应重点抓住它与椭圆的不同点:
(1)双曲线的定义中是动点到两个定点的距离的差的绝对值等于非零常数,而不是差等于常数,否则轨迹只能为双曲线的某一支,设F1,F2表示双曲线的左、右焦点.
①若|MF1|-|MF2|=2a,则点M在右支上;②若|MF2|-|MF1|=2a,则点M在左支上.
(2)双曲线的定义中,常数应小于两个已知定点间的距离且不等于0,否则:
①若常数等于|F1F2|,则轨迹为两条射线;②若常数等于0,则轨迹为线段F1F2的垂直平分线;③若常数大于|F1F2|,则轨迹不存在.【做一做1】 (1)给出下列条件,其中动点轨迹为双曲线的是( )
A.动点P到点(3,0)及点(-3,0)的距离之差的绝对值等于8
B.动点P到点(3,0)及点(-3,0)的距离之差等于6
C.动点P到点(3,0)及点(-3,0)的距离之差的绝对值等于4
D.动点P到点(3,0)及点(-3,0)的距离之和等于4
(2)已知动点P到点M(1,0)及点N(3,0)的距离之差为2,则点P的轨迹是( )
A.双曲线 B.双曲线的一支
C.两条射线 D.一条射线
解析:(1)由双曲线的定义知C项正确.
(2)|PM|-|PN|=2,而|MN|=2,所以点P在线段MN的延长线上.
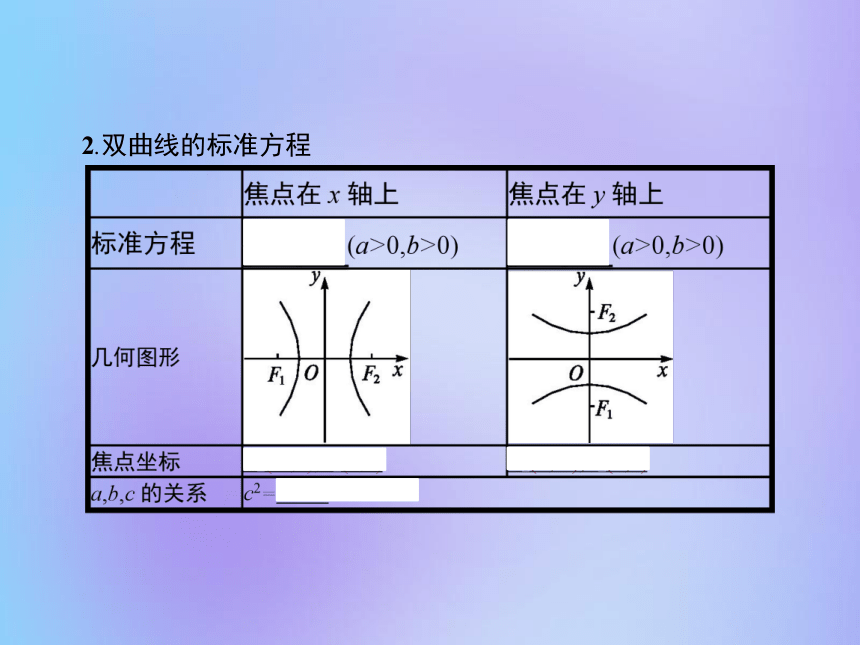
答案:(1)C (2)D2.双曲线的标准方程 名师点拨1.两双曲线 (a>0,b>0)的相同点是:它们的形状、大小都相同,都有a>0,b>0,a2+b2=c2;不同点是:两双曲线的位置不同,它们的焦点坐标也不同.
2.双曲线的焦点在x轴上?标准方程中x2项的系数为正;双曲线的焦点在y轴上?标准方程中y2项的系数为正,这是判断双曲线焦点所在坐标轴的重要方法.
3.双曲线的标准方程可统一表示为:mx2+ny2=1(mn<0).思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.答案:(1)× (2)√ (3)√ (4)× 探究一探究二探究三思维辨析对双曲线定义的理解 A.椭圆 B.双曲线
C.两条射线 D.双曲线的一支
思路点拨:结合已知等式以及两点间的距离公式进行分析判断.答案:B 探究一探究二探究三思维辨析反思感悟根据定义判断动点的轨迹是否为双曲线,务必要考虑定义中的条件:到两个定点的距离的差的绝对值等于常数,且这个常数既要不等于0,又要小于两个定点之间的距离.不能一看到动点到两个定点的距离之差的绝对值是个常数,就认定其轨迹为双曲线.探究一探究二探究三思维辨析变式训练1已知两定点F1(-3,0),F2(3,0),在满足下列条件的平面内动点P的轨迹中,是双曲线的是 ( )
A.||PF1|-|PF2||=5 B.||PF1|-|PF2||=6
C.||PF1|-|PF2||=7 D.||PF1|-|PF2||=0
解析:A中,因为|F1F2|=6,所以||PF1|-|PF2||=5<|F1F2|,故动点P的轨迹是双曲线;B中,因为||PF1|-|PF2||=6=|F1F2|,所以动点P的轨迹是以F1或F2为端点的射线(含端点);C中,因为||PF1|-|PF2||=7>|F1F2|,所以动点P的轨迹不存在;D中,因为||PF1|-|PF2||=0,即|PF1|=|PF2|,根据线段垂直平分线的性质,动点P的轨迹是线段F1F2的垂直平分线,故选A.
答案:A探究一探究二探究三思维辨析对双曲线标准方程的理解
【例2】 已知曲线方程 .
(1)若方程表示双曲线,求实数m的取值范围;
(2)若方程表示焦点在y轴上的双曲线,求实数m的取值范围;
(3)若方程表示椭圆,求实数m的取值范围.
思路点拨:根据双曲线与椭圆的标准方程的特征建立不等式(组)求解.
自主解答:(1)依题意有(m-1)(m2-4)>0,即(m-1)(m+2)(m-2)>0,解得-22.探究一探究二探究三思维辨析反思感悟给出方程 ,则该方程:
(1)表示双曲线的条件是mn>0;
(2)表示焦点在x轴上的双曲线的条件是m>0,n>0;
(3)表示焦点在y轴上的双曲线的条件是m<0,n<0;
(4)表示椭圆的条件是m>0,n<0.探究一探究二探究三思维辨析变式训练2(1)若方 表示双曲线,则实数m的取值范围是( )
A.-1-1
C.m>3 D.m<-1
(2)在方程mx2-my2=3n中,若mn<0,则该方程表示( )
A.焦点在x轴上的椭圆
B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆
D.焦点在y轴上的双曲线
解析:(1)依题意有m+1>0,所以m>-1.答案:(1)B (2)D 探究一探究二探究三思维辨析求双曲线的标准方程
【例3】根据下列条件求双曲线的标准方程.思路点拨:先根据已知条件设出双曲线的标准方程,再构造关于a,b的方程组,求得a,b即得方程,要注意对双曲线焦点位置的分析以及平方关系c2=a2+b2的运用.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3求满足下列条件的双曲线的标准方程:
(1)一个焦点是(0,-6),经过点A(-5,6);
(2)过M(1,1),N(-2,5)两点.探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视对双曲线焦点位置的讨论致误
【典例】 若双曲线 的焦距等于6,求实数m的值.
易错分析:本题常见错误是误认为双曲线焦点一定在x轴上,漏掉焦点在y轴上的情况,从而出现丢解.
自主解答:因为双曲线的焦距等于6,即2c=6,所以c=3,a2+b2=c2=9.纠错心得:在解决双曲线问题时,当双曲线的焦距已知时,并不能确定焦点在x轴上还是在y轴上,因此要注意对双曲线焦点位置的讨论,避免出现丢解.探究一探究二探究三思维辨析跟踪训练若双曲线 的一个焦点到中心的距离为3,则m的值等于 .?
解析:(1)当焦点在x轴上,有m>5,则c2=m+m-5=9,所以 m=7;
(2)当焦点在y轴上,有m<0,则c2=-m+5-m=9,所以 m=-2.
综上所述,m=7或m=-2.
答案:7或-21.已知A(-3,0),B(3,0),若动点M满足||MA|-|MB||=4,则点M的轨迹是( )
A.双曲线 B.双曲线的左支
C.双曲线的右支 D.两条射线
解析:根据双曲线的定义知,动点M的轨迹是焦点在x轴上的双曲线.
答案:A解析:由双曲线的标准方程,知a=4,b=3,所以c=5,又由于焦点在x轴上.所以焦点为(-5,0),(5,0).
答案:C
(1)双曲线的定义中是动点到两个定点的距离的差的绝对值等于非零常数,而不是差等于常数,否则轨迹只能为双曲线的某一支,设F1,F2表示双曲线的左、右焦点.
①若|MF1|-|MF2|=2a,则点M在右支上;②若|MF2|-|MF1|=2a,则点M在左支上.
(2)双曲线的定义中,常数应小于两个已知定点间的距离且不等于0,否则:
①若常数等于|F1F2|,则轨迹为两条射线;②若常数等于0,则轨迹为线段F1F2的垂直平分线;③若常数大于|F1F2|,则轨迹不存在.【做一做1】 (1)给出下列条件,其中动点轨迹为双曲线的是( )
A.动点P到点(3,0)及点(-3,0)的距离之差的绝对值等于8
B.动点P到点(3,0)及点(-3,0)的距离之差等于6
C.动点P到点(3,0)及点(-3,0)的距离之差的绝对值等于4
D.动点P到点(3,0)及点(-3,0)的距离之和等于4
(2)已知动点P到点M(1,0)及点N(3,0)的距离之差为2,则点P的轨迹是( )
A.双曲线 B.双曲线的一支
C.两条射线 D.一条射线
解析:(1)由双曲线的定义知C项正确.
(2)|PM|-|PN|=2,而|MN|=2,所以点P在线段MN的延长线上.
答案:(1)C (2)D2.双曲线的标准方程 名师点拨1.两双曲线 (a>0,b>0)的相同点是:它们的形状、大小都相同,都有a>0,b>0,a2+b2=c2;不同点是:两双曲线的位置不同,它们的焦点坐标也不同.
2.双曲线的焦点在x轴上?标准方程中x2项的系数为正;双曲线的焦点在y轴上?标准方程中y2项的系数为正,这是判断双曲线焦点所在坐标轴的重要方法.
3.双曲线的标准方程可统一表示为:mx2+ny2=1(mn<0).思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.答案:(1)× (2)√ (3)√ (4)× 探究一探究二探究三思维辨析对双曲线定义的理解 A.椭圆 B.双曲线
C.两条射线 D.双曲线的一支
思路点拨:结合已知等式以及两点间的距离公式进行分析判断.答案:B 探究一探究二探究三思维辨析反思感悟根据定义判断动点的轨迹是否为双曲线,务必要考虑定义中的条件:到两个定点的距离的差的绝对值等于常数,且这个常数既要不等于0,又要小于两个定点之间的距离.不能一看到动点到两个定点的距离之差的绝对值是个常数,就认定其轨迹为双曲线.探究一探究二探究三思维辨析变式训练1已知两定点F1(-3,0),F2(3,0),在满足下列条件的平面内动点P的轨迹中,是双曲线的是 ( )
A.||PF1|-|PF2||=5 B.||PF1|-|PF2||=6
C.||PF1|-|PF2||=7 D.||PF1|-|PF2||=0
解析:A中,因为|F1F2|=6,所以||PF1|-|PF2||=5<|F1F2|,故动点P的轨迹是双曲线;B中,因为||PF1|-|PF2||=6=|F1F2|,所以动点P的轨迹是以F1或F2为端点的射线(含端点);C中,因为||PF1|-|PF2||=7>|F1F2|,所以动点P的轨迹不存在;D中,因为||PF1|-|PF2||=0,即|PF1|=|PF2|,根据线段垂直平分线的性质,动点P的轨迹是线段F1F2的垂直平分线,故选A.
答案:A探究一探究二探究三思维辨析对双曲线标准方程的理解
【例2】 已知曲线方程 .
(1)若方程表示双曲线,求实数m的取值范围;
(2)若方程表示焦点在y轴上的双曲线,求实数m的取值范围;
(3)若方程表示椭圆,求实数m的取值范围.
思路点拨:根据双曲线与椭圆的标准方程的特征建立不等式(组)求解.
自主解答:(1)依题意有(m-1)(m2-4)>0,即(m-1)(m+2)(m-2)>0,解得-2
(1)表示双曲线的条件是mn>0;
(2)表示焦点在x轴上的双曲线的条件是m>0,n>0;
(3)表示焦点在y轴上的双曲线的条件是m<0,n<0;
(4)表示椭圆的条件是m>0,n<0.探究一探究二探究三思维辨析变式训练2(1)若方 表示双曲线,则实数m的取值范围是( )
A.-1
C.m>3 D.m<-1
(2)在方程mx2-my2=3n中,若mn<0,则该方程表示( )
A.焦点在x轴上的椭圆
B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆
D.焦点在y轴上的双曲线
解析:(1)依题意有m+1>0,所以m>-1.答案:(1)B (2)D 探究一探究二探究三思维辨析求双曲线的标准方程
【例3】根据下列条件求双曲线的标准方程.思路点拨:先根据已知条件设出双曲线的标准方程,再构造关于a,b的方程组,求得a,b即得方程,要注意对双曲线焦点位置的分析以及平方关系c2=a2+b2的运用.探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析探究一探究二探究三思维辨析变式训练3求满足下列条件的双曲线的标准方程:
(1)一个焦点是(0,-6),经过点A(-5,6);
(2)过M(1,1),N(-2,5)两点.探究一探究二探究三思维辨析探究一探究二探究三思维辨析忽视对双曲线焦点位置的讨论致误
【典例】 若双曲线 的焦距等于6,求实数m的值.
易错分析:本题常见错误是误认为双曲线焦点一定在x轴上,漏掉焦点在y轴上的情况,从而出现丢解.
自主解答:因为双曲线的焦距等于6,即2c=6,所以c=3,a2+b2=c2=9.纠错心得:在解决双曲线问题时,当双曲线的焦距已知时,并不能确定焦点在x轴上还是在y轴上,因此要注意对双曲线焦点位置的讨论,避免出现丢解.探究一探究二探究三思维辨析跟踪训练若双曲线 的一个焦点到中心的距离为3,则m的值等于 .?
解析:(1)当焦点在x轴上,有m>5,则c2=m+m-5=9,所以 m=7;
(2)当焦点在y轴上,有m<0,则c2=-m+5-m=9,所以 m=-2.
综上所述,m=7或m=-2.
答案:7或-21.已知A(-3,0),B(3,0),若动点M满足||MA|-|MB||=4,则点M的轨迹是( )
A.双曲线 B.双曲线的左支
C.双曲线的右支 D.两条射线
解析:根据双曲线的定义知,动点M的轨迹是焦点在x轴上的双曲线.
答案:A解析:由双曲线的标准方程,知a=4,b=3,所以c=5,又由于焦点在x轴上.所以焦点为(-5,0),(5,0).
答案:C
